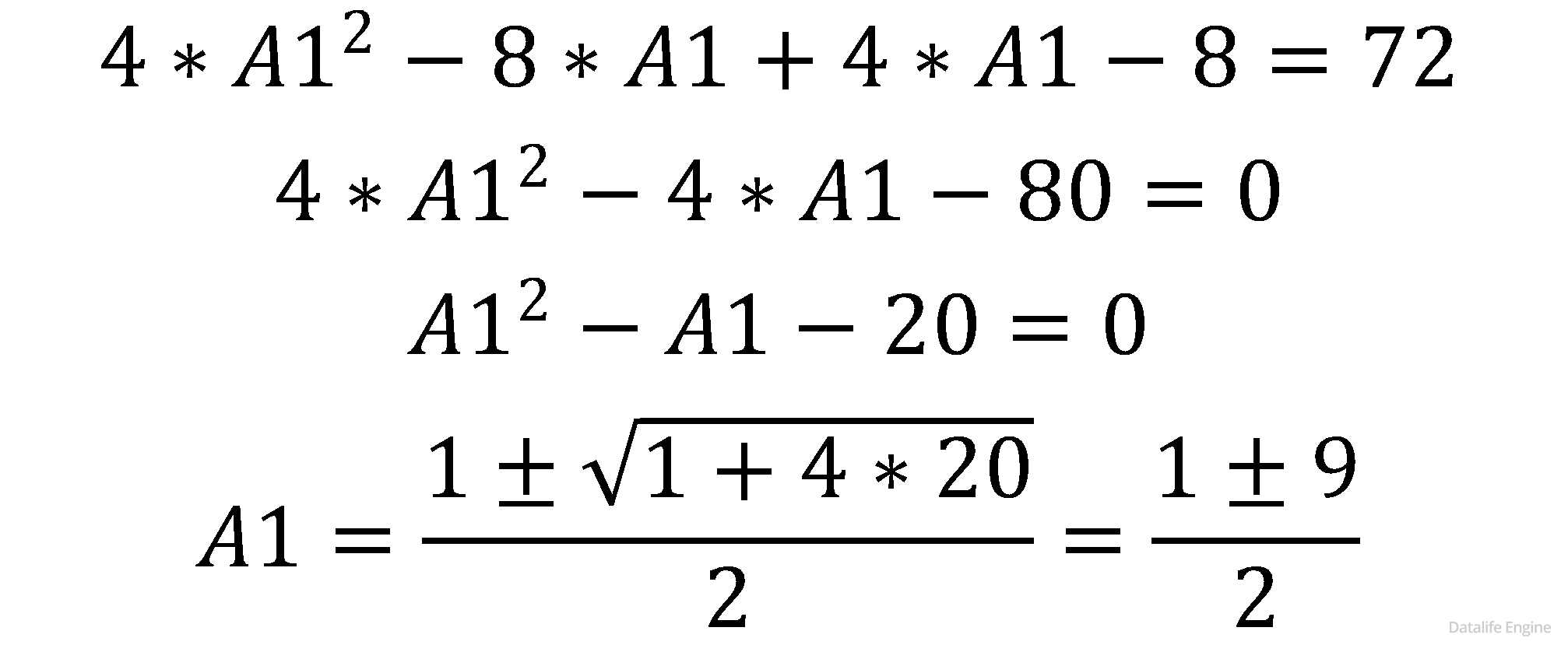Задача 5.4.1. Дан фрагмент электронной таблицы.
|
А
|
B
|
C
|
D
|
|
1
|
9
|
...
|
2
|
5
|
|
2
|
=B2+C2+D2
|
=C2
|
=(A1–D1)*(B1-5)
|
=(A1–D1)*C1
|
Какое целое число должно быть записано в ячейке B1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:D2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.
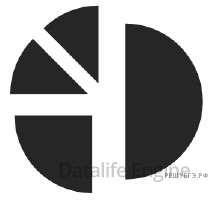
Подставим в формулы все числа, какие возможно:
|
А
|
B
|
C
|
D
|
|
1
|
9
|
...
|
2
|
5
|
|
2
|
=B2+C2+D2
|
=C2
|
=(9–5)*(B1-5)
|
=(9–5)*2
|
Посчитаем то, что получится, и подставим вновь полученные значения:
|
А
|
B
|
C
|
D
|
|
1
|
9
|
...
|
2
|
5
|
|
2
|
=B2+4*(B1-5)+8
|
=4*(B1-5)
|
=4*(B1-5)
|
8
|
Из диаграммы видно, что в двух ячейках находятся одинаковые величины. Им соответствуют ячейки В2 и С2. Так как значения ячеек неотрицательны, то A2 > D2. Из диаграммы видно, что четвертинка диаграммы соответствует ячейке D2, то есть четвертинка равна 8. Следовательно, восьмушка равна 4.
B2 = 4
4 * (B1 – 5) = 4
B1 = 6
Ответ: 6.
Задача 5.4.2. Дан фрагмент электронной таблицы.
|
A
|
B
|
C
|
|
1
|
|
3
|
10
|
|
2
|
=(A1-3)/(B1+3)
|
=(A1-2)/(C1-3)
|
= C1/(A1 – 4)
|
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Подставим все возможные значения в таблицу:
|
A
|
B
|
C
|
|
1
|
|
3
|
10
|
|
2
|
=(A1-3)/(3+3)
|
=(A1-2)/(10-3)
|
= 10/(A1 – 4)
|
Посчитаем:
|
A
|
B
|
C
|
|
1
|
|
3
|
10
|
|
2
|
=(A1-3)/6
|
=(A1-2)/7
|
= 10/(A1 – 4)
|
Из диаграммы видно, что две ячейки равны. Предположим, что А1=B1, тогда
(A1 – 3)/6 = (A1 – 2)/7
Решим уравнение:
(A1 – 3) * 7 = (A1-2)*6
7 * А1 – 21 = 6 * А1 – 12
А1 = 9.
Теперь надо посчитать значение ячеек нижней строки и убедиться, что в соответствии с диаграммой ячейка С2 в два раза больше, чем A1 и B1:
|
A
|
B
|
C
|
|
1
|
9
|
3
|
10
|
|
2
|
=(9-3)/6
|
=(9-2)/7
|
= 10/(9 – 4)
|
Посчитаем значения ячеек:
Нижняя строка соответствует диаграмме. Если бы соответствия не было, пришлось бы приравнять другую пару ячеек.
Ответ: 9.
Задача 5.4.3. Дан фрагмент электронной таблицы.
|
A
|
B
|
C
|
|
1
|
|
4
|
6
|
|
2
|
= (A1 − 2)/(B1 − 1)
|
= C1*B1/(4*A1 + 4)
|
= C1/(A1 − 2)
|
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Подставим все возможные значения:
|
A
|
B
|
C
|
|
1
|
|
4
|
6
|
|
2
|
= (A1 − 2)/(4 − 1)
|
= 6*4/(4*A1 + 4)
|
= 6/(A1 − 2)
|
Посчитаем:
|
A
|
B
|
C
|
|
1
|
|
4
|
6
|
|
2
|
= (A1 − 2)/3
|
= 24/(4*A1 + 4)
|
= 6/(A1 − 2)
|
Из диаграммы видно, что две ячейки равны между собой, а третья в два раза больше.
Если приравнять А2 и В2 или А2 и С2, то мы получим квадратное уравнение. Из двух возможных корней после проверки оставим 1. Если же приравнять В2 и С2, то получим линейное уравнение. Начнем с него:
24/(4 * A1 + 4) = 6/(A1 − 2)
24 * (A1 − 2) = 6 * (4 * A1 + 4)
24 * А1 – 48 = 24 * А1 + 24
– 48 = 24.
Нет корней.
Приравняем А2 и B2:
(A1 − 2) / 3 = 24 / (4 * A1 + 4)
(A1 − 2) * (4*A1 + 4) = 72
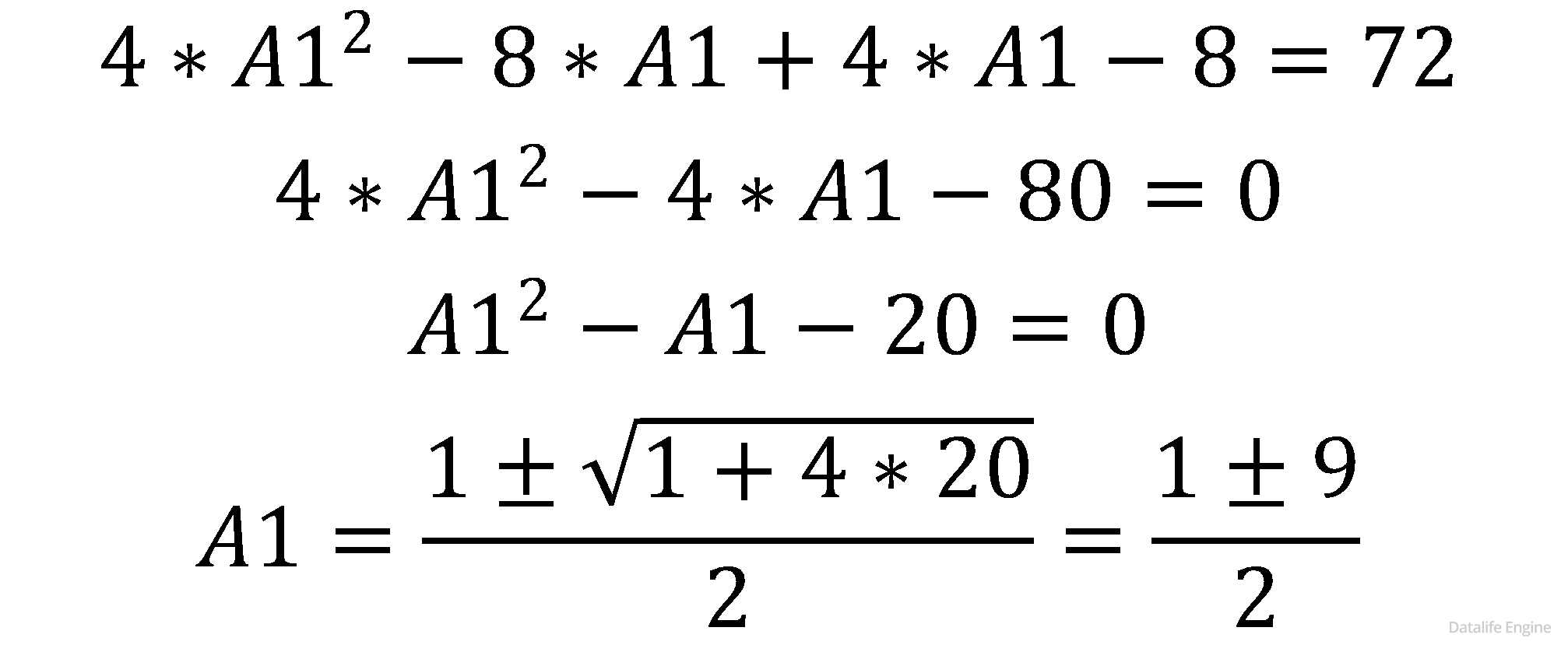
Мы получили два корня:
А1 = – 4 и А1 = 5
Проверим корень А1=-4:
|
A
|
B
|
C
|
|
1
|
-4
|
4
|
6
|
|
2
|
= (-4 − 2)/3
|
= 24/(4*(-4) + 4)
|
= 6/(-4 − 2)
|
Получаются отрицательные значения.
Проверим А1 = 5
|
A
|
B
|
C
|
|
1
|
5
|
4
|
6
|
|
2
|
= (5 − 2)/3
|
= 24/(4*5 + 4)
|
= 6/(5 − 2)
|
Посчитаем:
Нижняя строка соответствует диаграмме.
Ответ: 5.