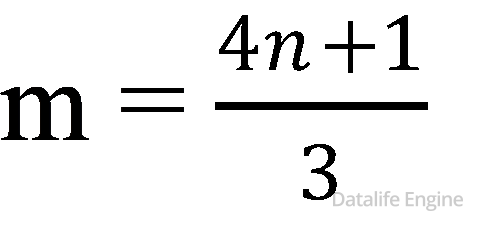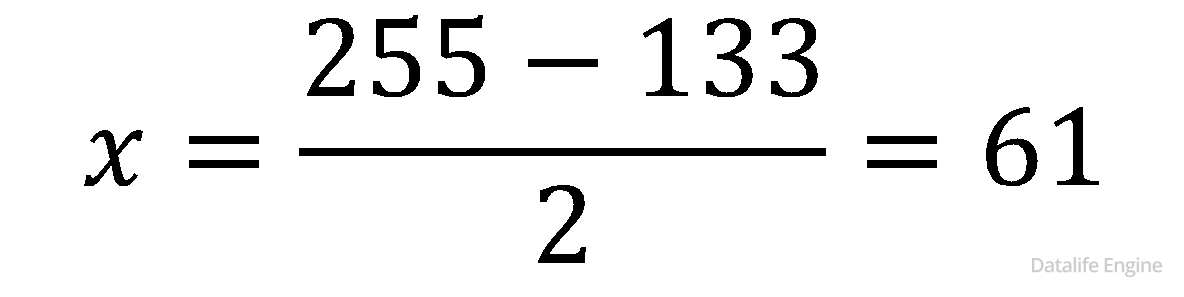Задача 6.2.1. Автомат получает на вход трёхзначное число. По этому числу строится новое число по следующим правилам.
1. Складываются первая и вторая, а также вторая и третья цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке убывания (без разделителей).
Пример. Исходное число: 348. Суммы: 3 + 4 = 7; 4 + 8 = 12. Результат: 127. Укажите наименьшее число, в результате обработки которого автомат выдаст число 1412.
Задача 6.2.2. Автомат получает на вход четырёхзначное число. По этому числу строится новое число по следующим правилам:
1. Складываются первая и вторая, а также третья и четвёртая цифры исходного числа.
2. Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).
Пример. Исходное число: 2366. Суммы: 2 + 3 = 5; 6 + 6 = 12. Результат: 512. Укажите наибольшее число, в результате обработки которого автомат выдаст число 117.
Задача 6.2.3. Автомат получает на вход четырёхзначное число (число не может начинаться с нуля). По этому числу строится новое число по следующим правилам:
1. Складываются отдельно первая и вторая, вторая и третья, третья и четвёртая цифры заданного числа.
2. Наименьшая из полученных трёх сумм удаляется.
3. Оставшиеся две суммы записываются друг за другом в порядке неубывания без разделителей.
Пример. Исходное число: 1984. Суммы: 1 + 9 = 10, 9 + 8 = 17, 8 + 4 = 12. Удаляется 10. Результат: 1217.
Укажите наибольшее число, при обработке которого автомат выдаёт результат 613.
Задача 6.2.4. Автомат получает на вход нечётное число X. По этому числу строится трёхзначное число Y по следующим правилам.
1. Первая цифра числа Y (разряд сотен) — остаток от деления X на 4.
2. Вторая цифра числа Y (разряд десятков) — остаток от деления X на 3.
3. Третья цифра числа Y (разряд единиц) — остаток от деления X на 2.
Пример.
Исходное число: 63179. Остаток от деления на 4 равен 3; остаток от деления на 3 равен 2; остаток от деления на 2 равен 1. Результат работы автомата: 321.
Укажите наименьшее двузначное число, при обработке которого автомат выдаёт результат 101.
Примечание. На остатки от деления есть программистская задача, которая намного труднее. Поэтому вышеуказанную задачу можно считать разминкой.
Задача 6.2.5. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1) Строится двоичная запись числа N.
2) К этой записи дописываются справа ещё два разряда по следующему правилу:
а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.
Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.
Задача 6.2.6. Автомат обрабатывает натуральное число N (0 ≤ N ≤ 255) по следующему алгоритму:
1. Строится восьмибитная двоичная запись числа N.
2. Все цифры двоичной записи заменяются на противоположные (0 на 1, 1 на 0).
3. Полученное число переводится в десятичную запись.
4. Из нового числа вычитается исходное, полученная разность выводится на экран.
Пример. Дано число N = 13. Алгоритм работает следующим образом.
1. Восьмибитная двоичная запись числа N: 00001101.
2. Все цифры заменяются на противоположные, новая запись 11110010.
3. Десятичное значение полученного числа 242.
4. На экран выводится число 242 − 13 = 229.
Какое число нужно ввести в автомат, чтобы в результате получилось 133?
Задача 6.2.7. Автомат убирает левую 1 из двоичной записи числа и вычитает полученное число из исходного. Числа от 10 до 1000. Сколько различных чисел получится в результате работы автомата, если вводятся на обработку числа от 10 до 1000.