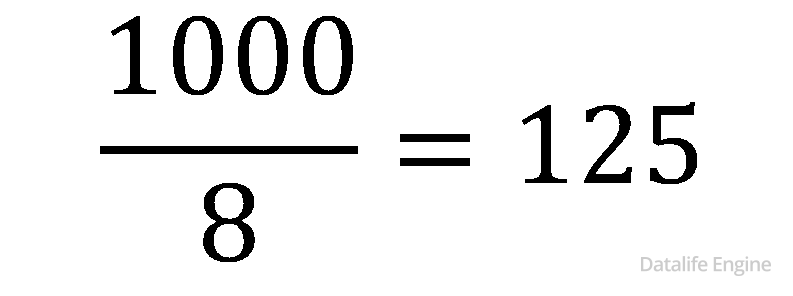Задача 6.5.1. Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v, w).
Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды
заменить (555, 63)
преобразует строку 12555550 в строку 1263550.
Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.
Цикл
ПОКА условие
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ условие
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно).
Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 1000 идущих подряд цифр 9? В ответе запишите полученную строку.
НАЧАЛО
ПОКА нашлось (999) ИЛИ нашлось (888)
ЕСЛИ нашлось (888)
ТО заменить (888, 9)
ИНАЧЕ заменить (999, 8)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Дано 1000 «9» = «999» + 997 «9»
Первые три девятки исполнитель заменит на одну восьмерку:
«999» + 997 «9» → «8» + 997 «9»
Далее исполнитель заменит еще две тройки девяток на две восьмерки:
«8» + 977 «9» = «8» + «999» + «999» + 991 «9» → «888» + 991 «9»
Затем исполнитель заменит три восьмерки на девятку:
«888» + 911 «9» → «9» + 991 «9» = 992 «9»
То есть в ходе всех этих действий количество девяток сократилось на 8 штук.
И в дальнейшем девятки будут исчезать по восемь штук, то есть.
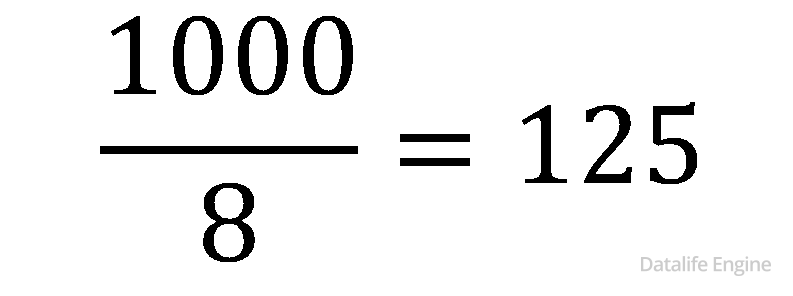
Поскольку 1000 делится на 8 без остатка, есть соблазн сказать, что цифр не останется вовсе, но это не так, потому что девятки исчезают по 9 штук, а затем возникает вместо них одна девятка. Следовательно, в какой-то момент у нас не хватит 9 девяток. Это произойдет на последних 8 девятках. Посмотрим, как они преобразуются:
«99999999» = «999» + «999» + «99» → «8» + «8» + «99» = «8899»
Ответ: 8899.
Задача 6.5.2. Какая строка получится в результате применения приведённой ниже программы к строке вида 1…12…2 (39 единиц и 39 двоек)?
НАЧАЛО
ПОКА нашлось (111)
заменить (111, 2)
заменить (222, 1)
КОНЕЦ ПОКА
КОНЕЦ
Дано 39«1» + 39«2»
Проверим условие ПОКА нашлось (111). Условие истинно, так как в начале строки имеются три единички.
Выполняем заменить (111, 2):
39«1» + 39«2» → 1«2» + 36«1» + 39«2»
Далее выполняется второе действие цикла заменить (222, 1):
1«2» + 36«1» + 39«2» → 1«2» + 36«1» + 1«1» + 36«2» = 1«2» + 37«1» + 36«2»
Это может ввести в недоумение тех, кто привык программировать на нормальных языках программирования. В этой задаче отсутствует понятие «курсор». То есть наличие трех единичек в условии не означает, что далее мы обрабатываем именно эти и только эти единички. В теле цикла мы работаем со всей строкой.
То есть за первый проход цикла количество единичек сократилось на 2, количество подряд идущих двоек сократилось на 3, и в начале строки возникла одна двойка:
39«1» + 39«2» → 1«2» + 37«1» + 36«2»
Аналогично выполняем второй проход цикла:
1«2» + 37«1» + 36«2» → 2«2» + 35«1» + 33«2»
Выполнение третьего прогона цикла отличается от двух предыдущих:
2«2» + 35«1» + 33«2» → 3«2» + 32«1» + 33«2» → 1«1» + 32«1» + 33«2» = 33«1» + 33«2»
То есть действие заменить (222, 1) заменяет три двойки в начале строки.
Получается, что за три прогона цикла у нас исчезли шесть единиц и шесть двоек:
39«1» + 39«2» → 33«1» + 33«2»
Следующие три прогона цикла окажут такое же действие:
33«1» + 33«2» → 27«1» + 27«2»
Продолжим дальше:
27«1» + 27«2» → 21«1» + 21«2» → 15«1» + 15«2» → 9«1» + 9«2»
Рассмотрим окончание работы алгоритма подробнее. Имеем строку:
111 111 111 222 222 222 → 2 111 111 222 222 222 → 2 111 111 1 222 222
Следующий прогон:
2 111 111 1 222 222 → 2 2 111 1 222 222 → 2 2 111 1 1 222
Следующий прогон:
2 2 111 1 1 222 → 2 2 2 1 1 222 → 1 1 1 222
Последний прогон цикла:
111 222 → 2222 → 12
Ответ: 12.