Задача 3.3.1. Два игрока, Петя и Валя, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй - 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Игра завершается в тот момент, когда общее количество камней в двух кучах становится не менее 20. Если в момент завершения игры общее число камней в двух кучах не менее 35, то выиграл Валя, в противном случае - Петя. Кто выигрывает при безошибочной игре обоих игроков? Укажите стратегию выигрывающего игрока - какой ход он должен сделать в каждой из позиций, которые могут ему встретиться при правильной игре. Докажите, что описанная стратегия - выигрышная.
Стройте дерево решений следующим образом. Состояние – это значения сразу в двух кучах. Поскольку мы можем делать две операции сразу с двумя кучами, то каждое состояние на следующем шаге ветвится в четыре возможных состояния.
Петя ходит первый. После его хода получим следующие четыре состояния:

Ошибка 1. Если мы продолжим идти по уровням, как в предыдущем параграфе, то мы получим количество состояний, увеличивающееся в геометрической прогрессии:
4 * 4 = 16, 16 * 4 = 64, 64 * 4 = 256, 256 * 4 = 1024
Такой поиск называется поиском в ширину и неэффективен для нашей задачи, так как число состояний будет резко увеличиваться. Вместо этого будем стараться спускаться по одной ветке вниз (поиск в глубину). Возможно, мы сумеем сделать выводы по одной ветке, и другие нам рассматривать не придется.
Продолжение хода решения.
Целесообразно выбрать ветку с наибольшим значением, чтобы игра поскорее прекратилась, то есть (3, 12):
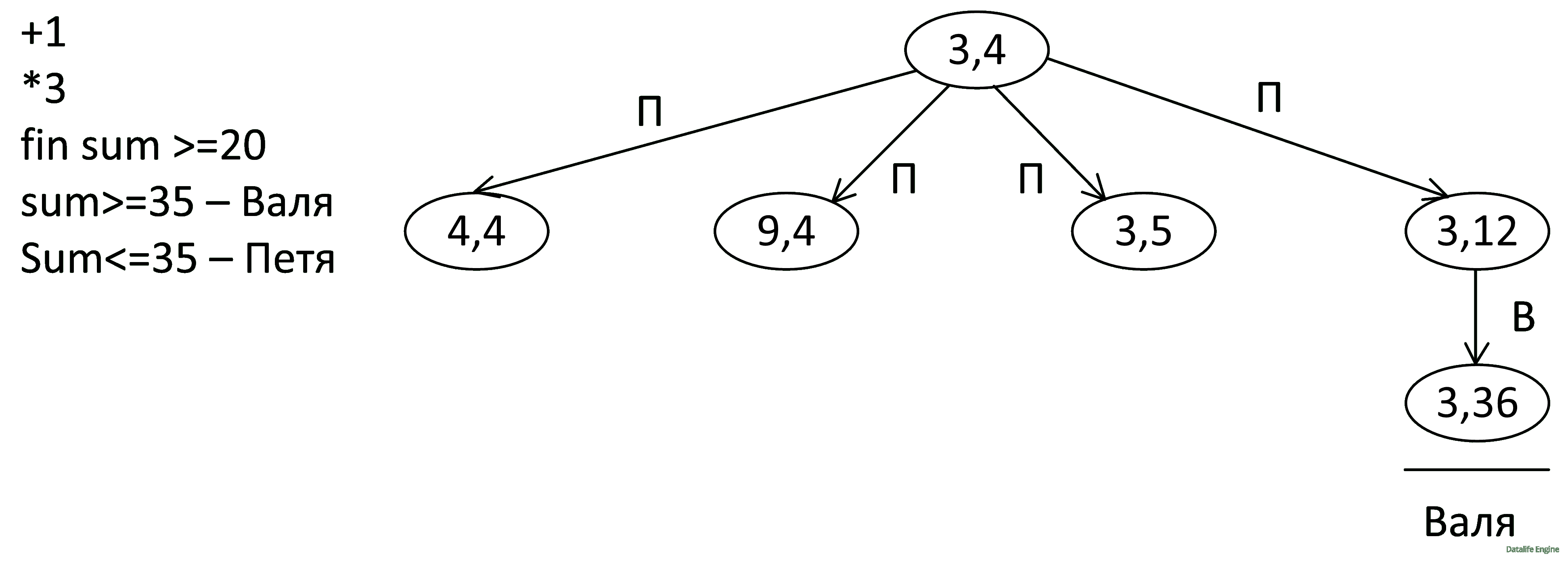
Заметим, что игроки делают беспроигрышные ходы. В нашем случае Валя сходит 12*3=36 и выиграет. Но это лишь означает, что Пете невыгоден ход, приведший к состоянию (3, 12):
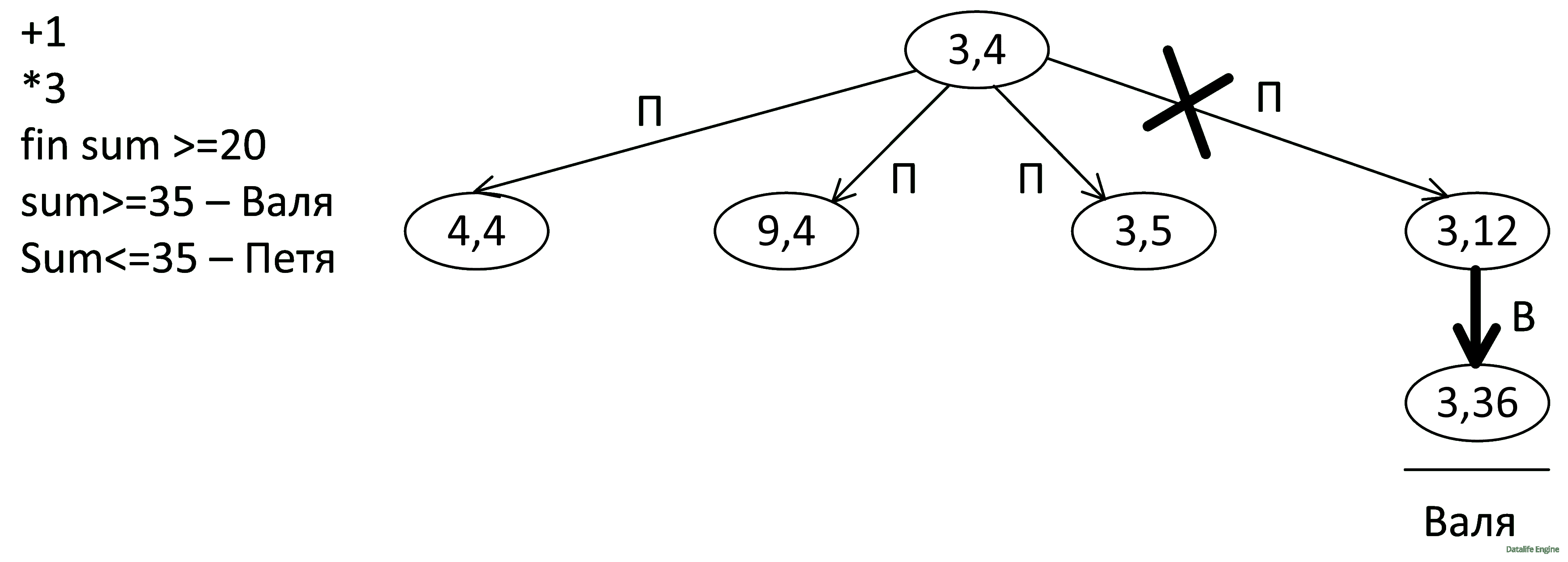
Поэтому надо рассмотреть следующую веточку Пети. С точки зрения больших чисел надо выбрать (9, 4). Но мы выберем (4, 4) из тех соображений, что от перестановки мест слагаемых сумма не меняется, а число камней в кучах одинаково. Следовательно, (4, 4) разветвится на два состояния, а не на 4:
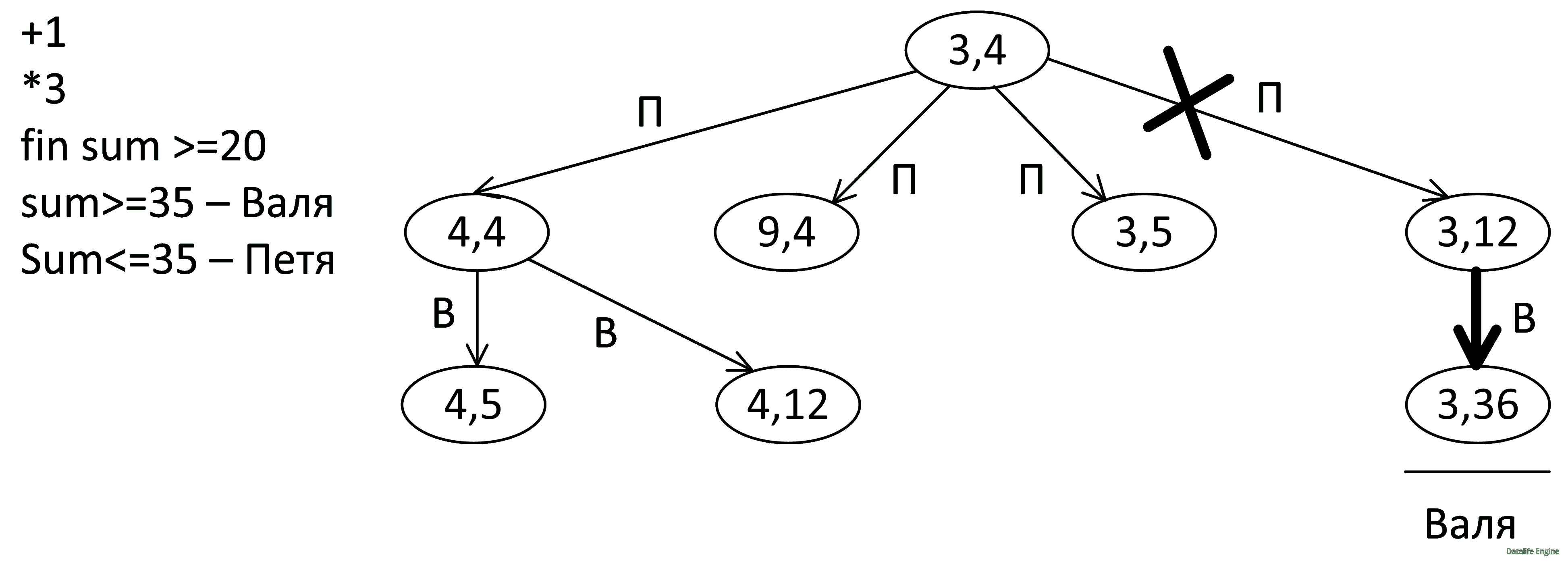
(4, 12) – Проигрышная позиция для Вали, так как Петя утроит 4 и получит 12 + 12 = 24:
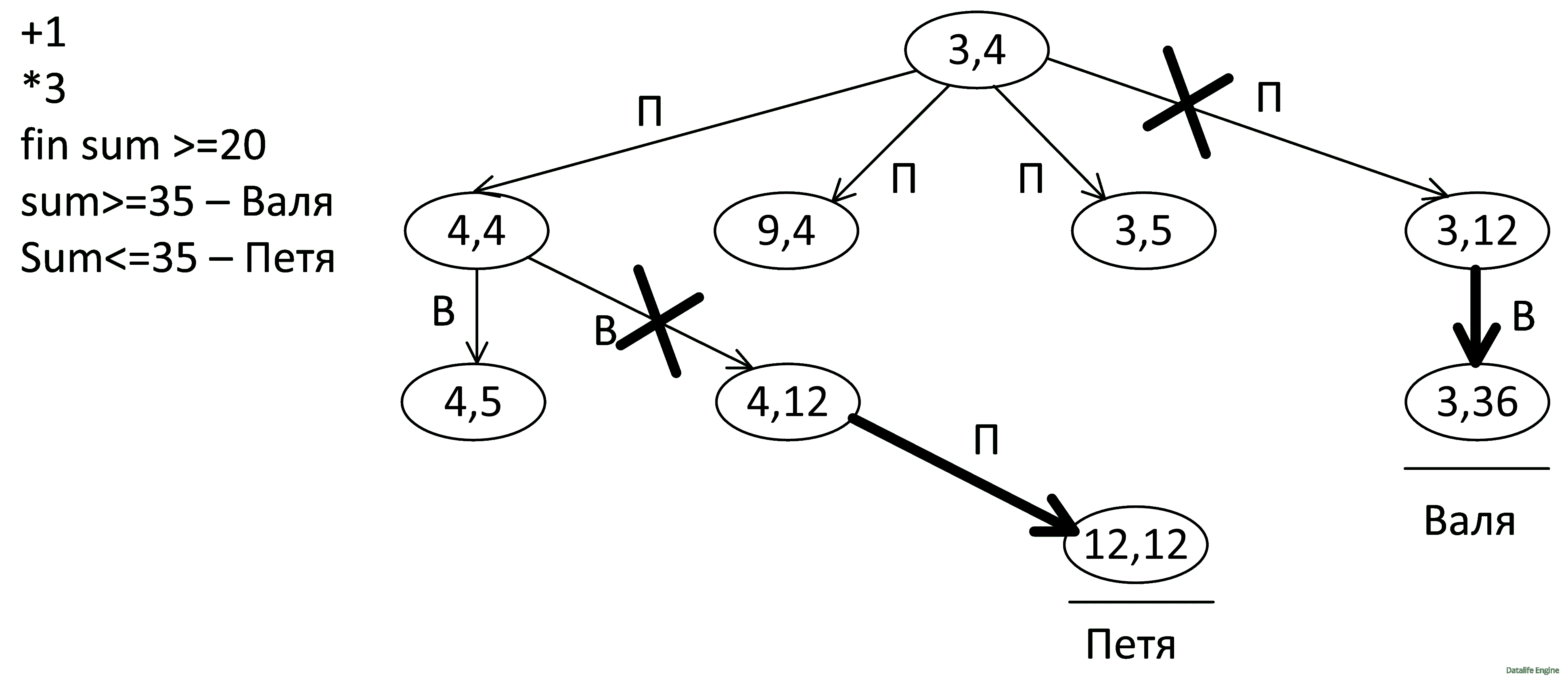
Но это лишь означает, что Валя не будет ходить в (4, 12), а сходит в (4, 5). Изучим ходы Пети оттуда:
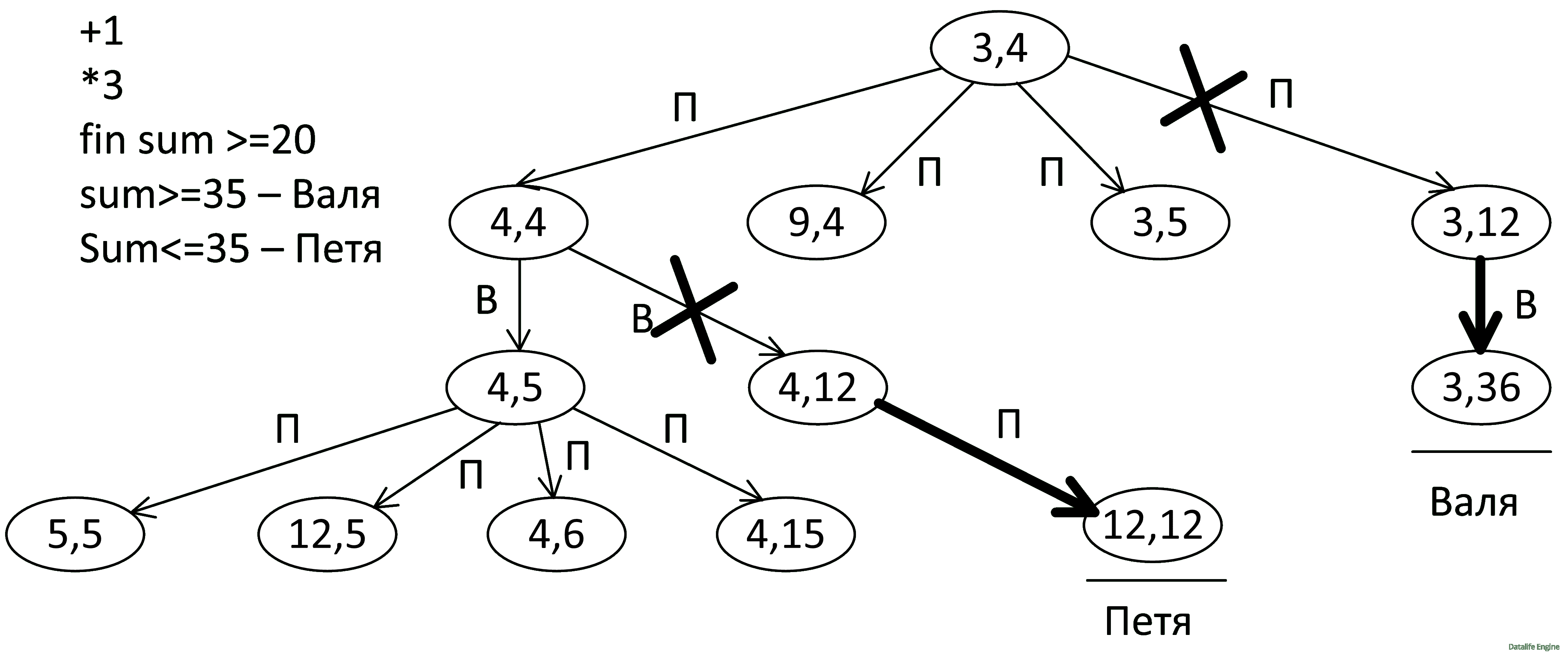
Скорее всего, (12, 5) и (4, 15) для Пети будут проигрышными, поэтому изучим состояние (5, 5):
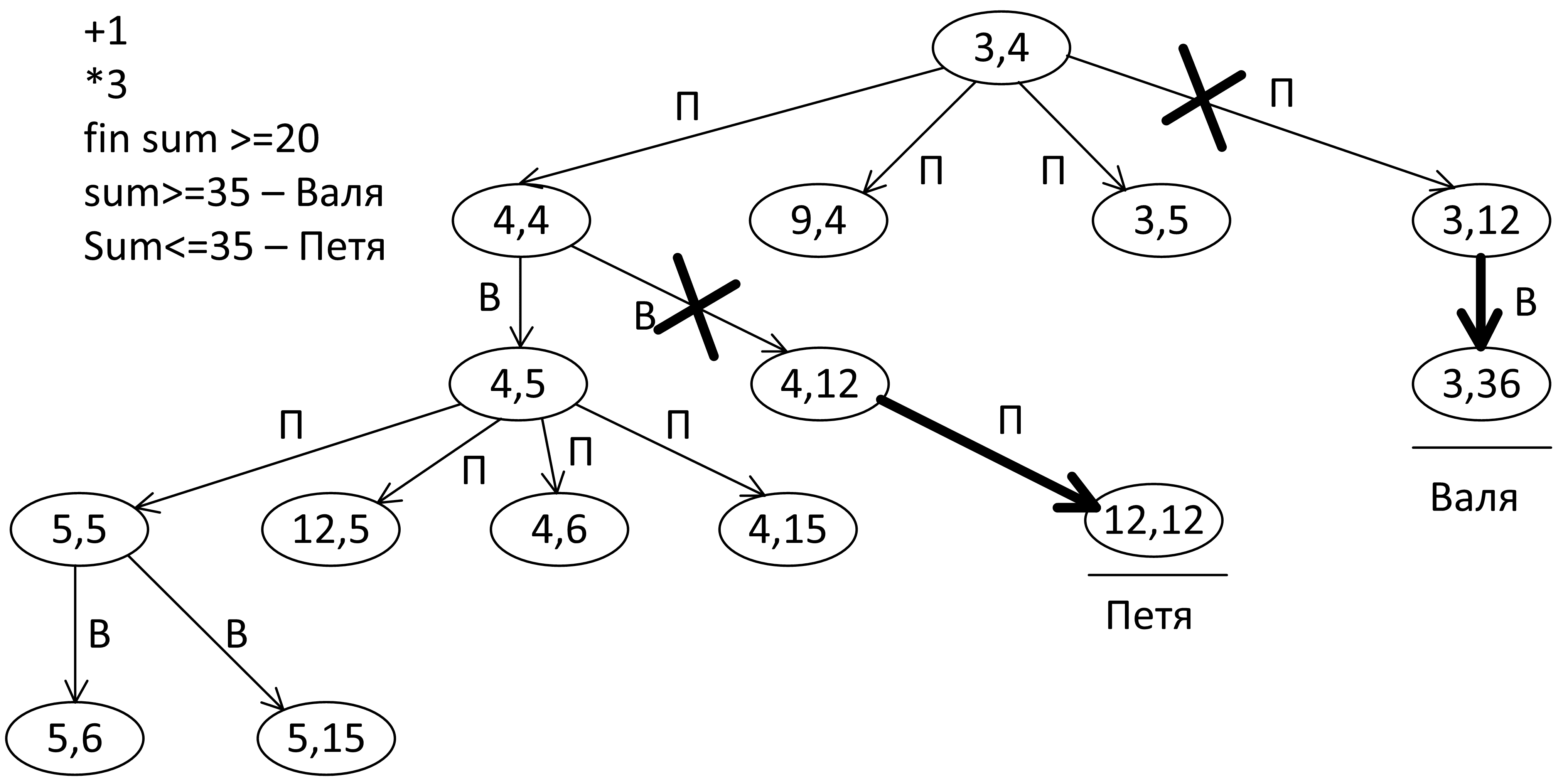
Рассмотрим состояние (5, 15). Петя выигрывает 5 * 3 + 15 = 30. Это означает, что Вале невыгодно туда ходить:
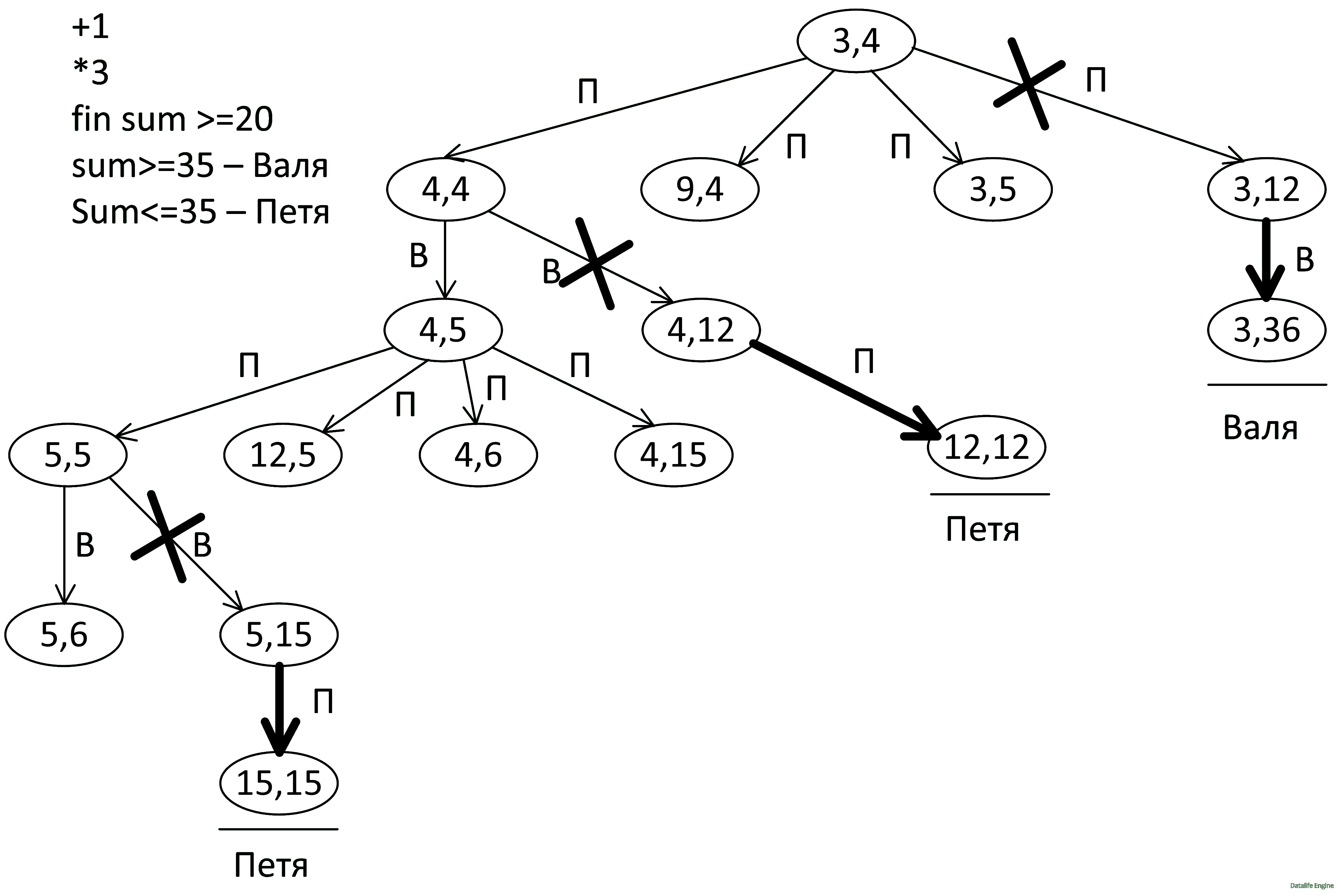
Исследуем позицию Вали (5, 6). Петя выигрывает 5 * 3 + 6 = 21:
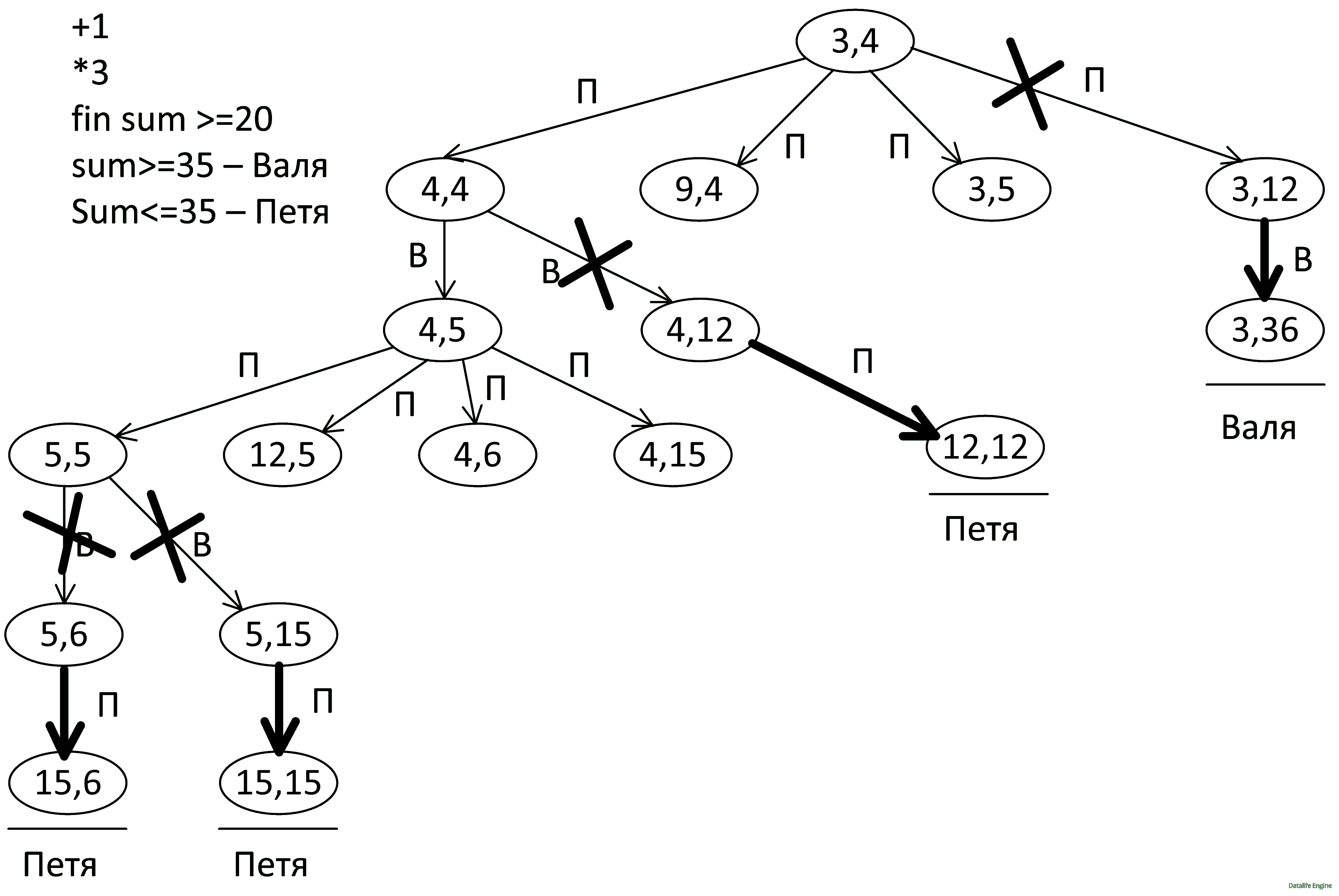
Получается, что из (5, 5) Валя проигрывает по всем веткам. Это значит, что Пете выгодно ходить из (4,5) → (5, 5):
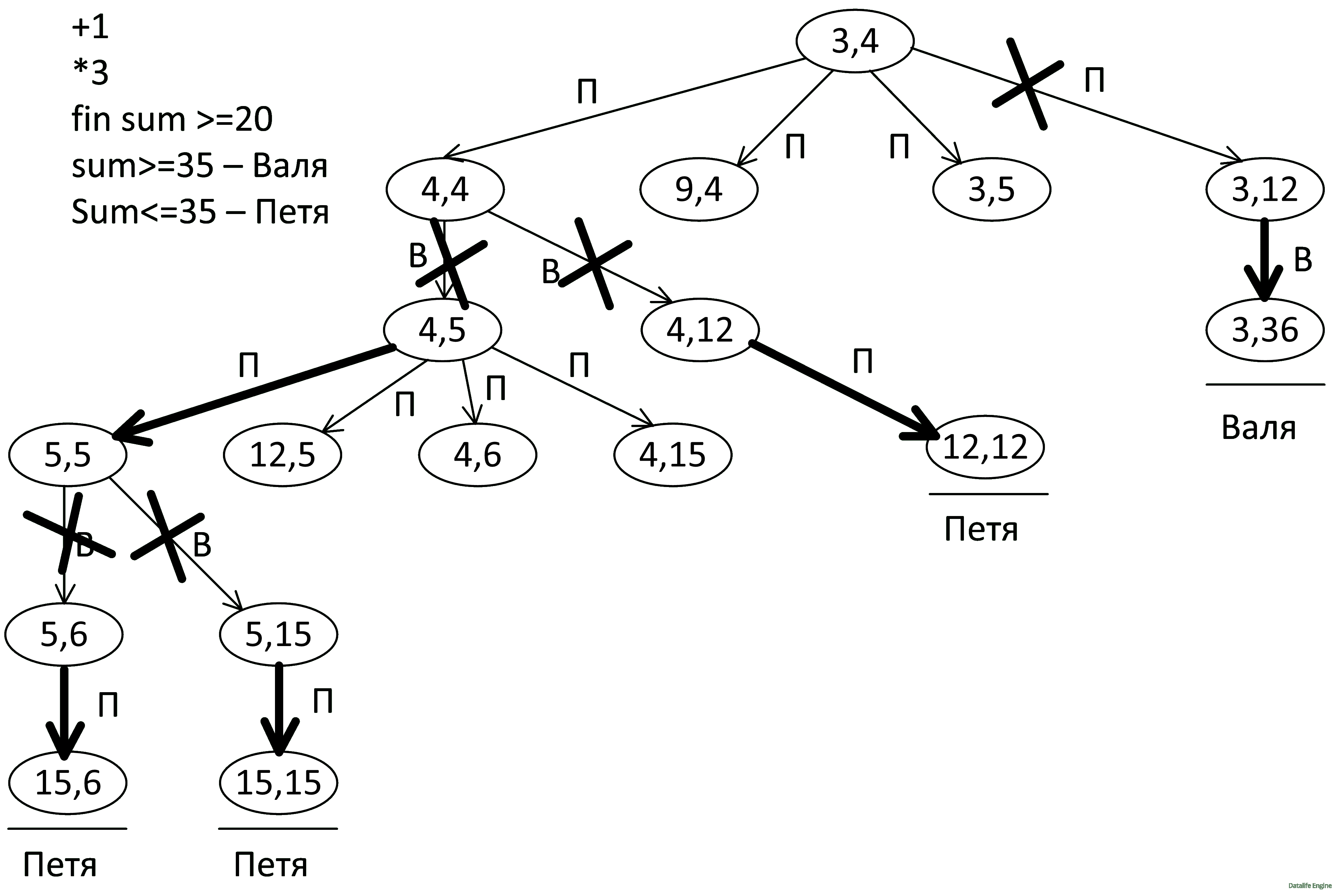
Получается, что в позиции (4, 4) Валя проигрывает в любом случае. То есть первый ход Пете выгодно делать такой: (3, 4) → (4, 4):
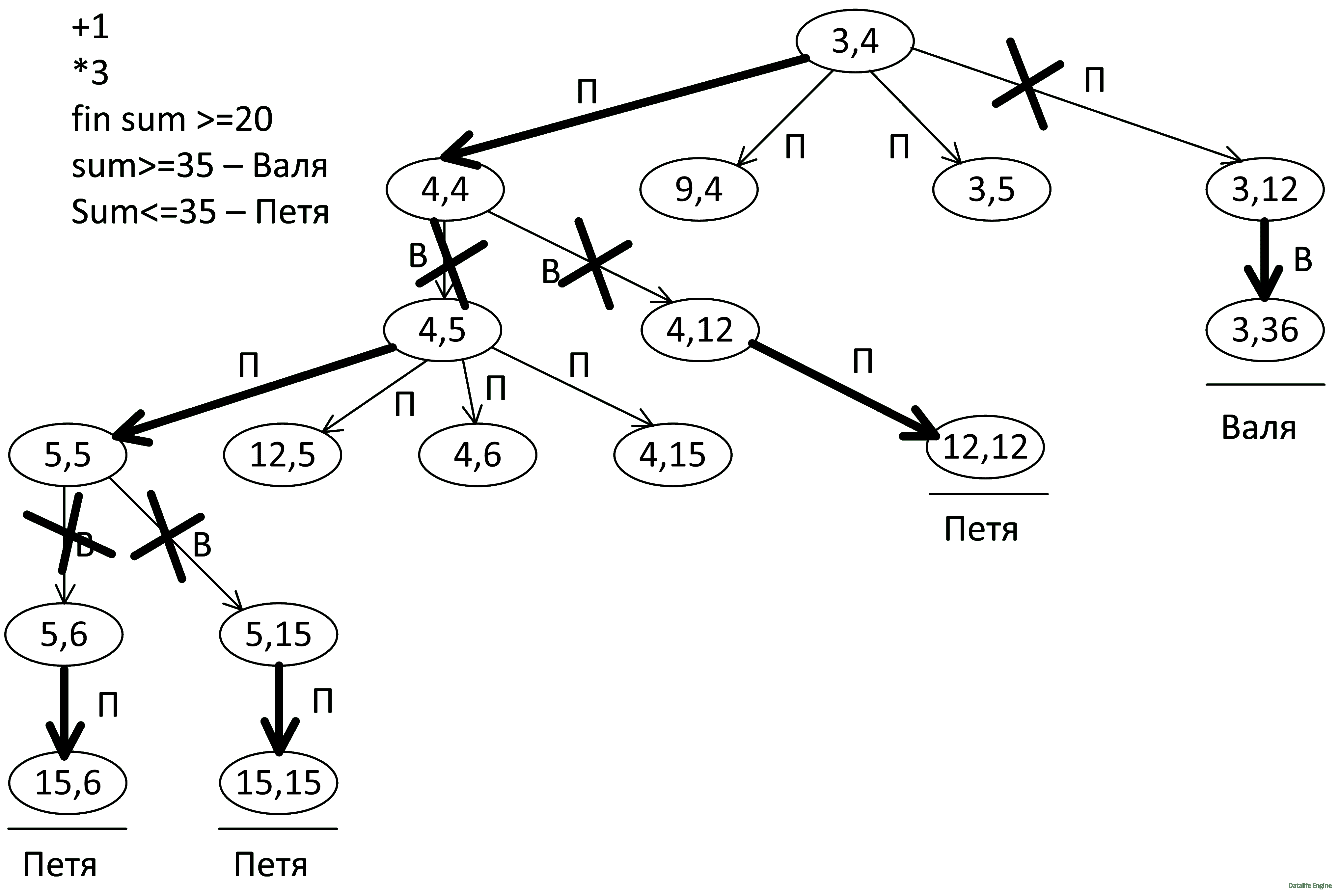
Итак, при правильной игре обоих игроков выиграет Петя. Заметим, что поиск в длину себя оправдал. Поскольку мы не ищем ходы, которые приведут к выигрышу как можно быстрее, мы не рассматриваем множество веточек в этом дереве. Кроме того, мы можем пожалеть проверяющего и не расписывать всё наше дерево, которое мы строили методом проб и ошибок.
Ответ. Поскольку мы утверждаем, что Петя выиграет, для него мы можем написать только выигрышные ходы. Но так как мы говорим, что Валя проиграет, то для него мы обязаны в качестве доказательства написать все его ходы. Так мы получим дерево, которое запишем в чистовик:
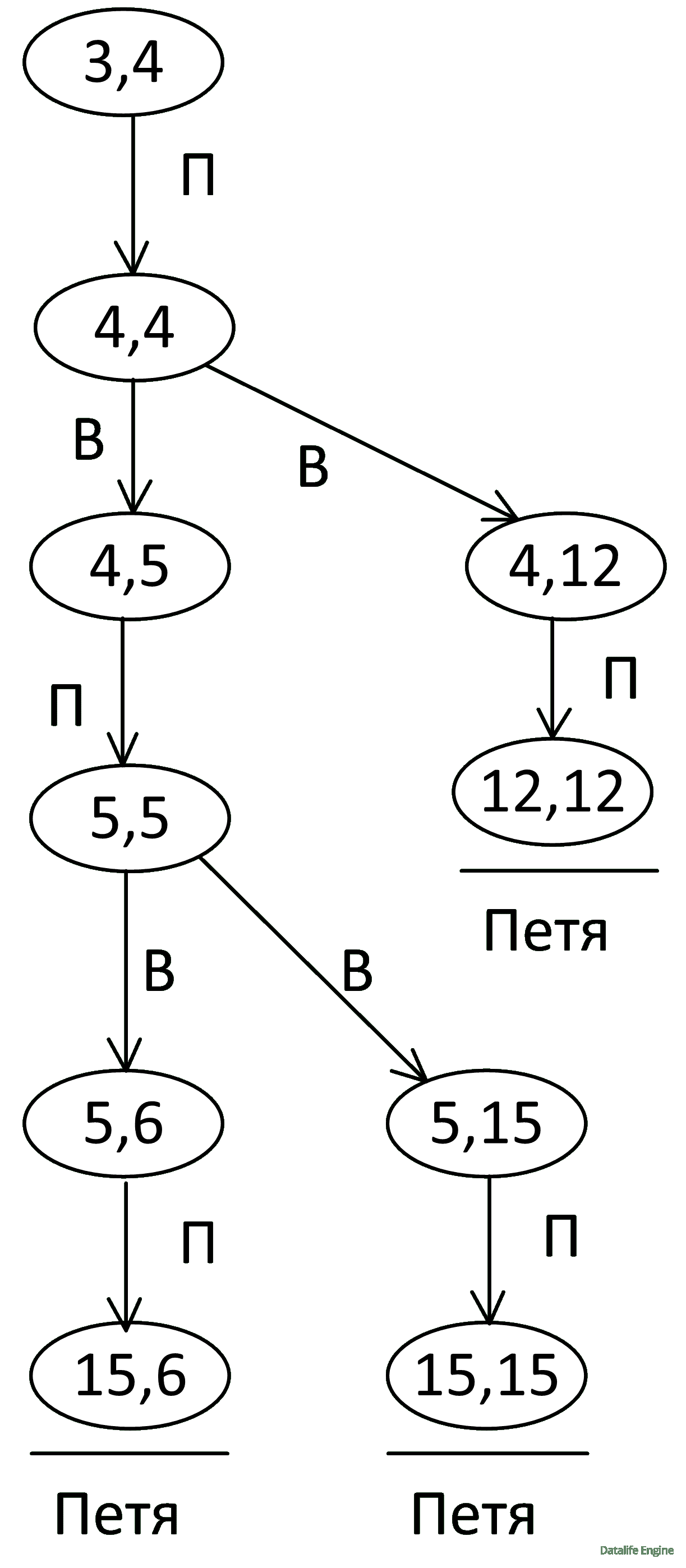
Задача 3.3.2. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу три камня или увеличить количество камней в куче в два раза. Игра завершается тогда, когда количество камней в куче становится ≥ 33. В начальный момент в куче было S камней: 1 ≤ S ≤ 32.
Задание 1. При каких S Петя выиграет своим первым ходом?
Будем рассматривать сначала большие состояния от 32 до 1, исследуя эти состояния.
Определим состояния, из которых игрок, находящийся там, выиграет за один ход с помощью удвоения:
32 / 2 + 1 = 17.
|
17
|
18
|
19
|
…
|
31
|
32
|
|
V1
|
V1
|
V1
|
…
|
V1
|
V1
|
Метка V1 означает выигрыш за один ход для того игрока, кто ходит с этого места.
Ответ: 17 ≤ S ≤ 32
Задание 2. При каких S Валя выиграет своим первым ходом?
Определите состояния, при которых любой игрок, ходящий оттуда, проиграет.
Из трех состояний: 14, 15, 16 с помощью хода +3 игрок попадает в состояния 17, 18, 19 (состояния V1), то есть выиграет его противник. А с помощью хода *2 игрок попадает в состояния 28, 30, 32 (состояния V1), то есть опять же его противник выиграет. Значит, состояния 14, 15, 16 являются проигрышными в любом случае:
|
14
|
15
|
16
|
17
|
18
|
19
|
…
|
31
|
32
|
|
X
|
X
|
X
|
V1
|
V1
|
V1
|
…
|
V1
|
V1
|
Ответ: 14, 15, 16
Задание 3. Назовите такие значения, при которых Петя выиграет своим вторым ходом независимо от игры Вали.
Найдите позиции, из которых можно сходить в проигрышную зону.
Мы можем отправить противника в проигрышную зону 14, 15, 16 с помощью хода +3 из 11, 12, 13. Поставим туда метку V2 (выигрыш за второй ход):
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
…
|
31
|
32
|
|
V2
|
V2
|
V2
|
X
|
X
|
X
|
V1
|
V1
|
V1
|
…
|
V1
|
V1
|
Ошибка. Вы ошибетесь, если вы ограничитесь только этими ходами. Ведь есть еще ходы *2.
Продолжение хода решения.
Найдем состояния, из которых можно загнать противника в проигрышные позиции с помощью хода *2:
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
…
|
31
|
32
|
|
V2
|
V2
|
|
|
V2
|
V2
|
V2
|
X
|
X
|
X
|
V1
|
V1
|
V1
|
…
|
V1
|
V1
|
Ответ: 7, 8, 11, 12, 13
Задание 4. Назовите два таких значения S, при которых Валя выигрывает своим первым или вторым ходом.
Исследуйте с помощью дерева те состояния с большими значениями, которые еще не были исследованы.
Построим деревья из нашей таблицы для состояний 9 и 10:
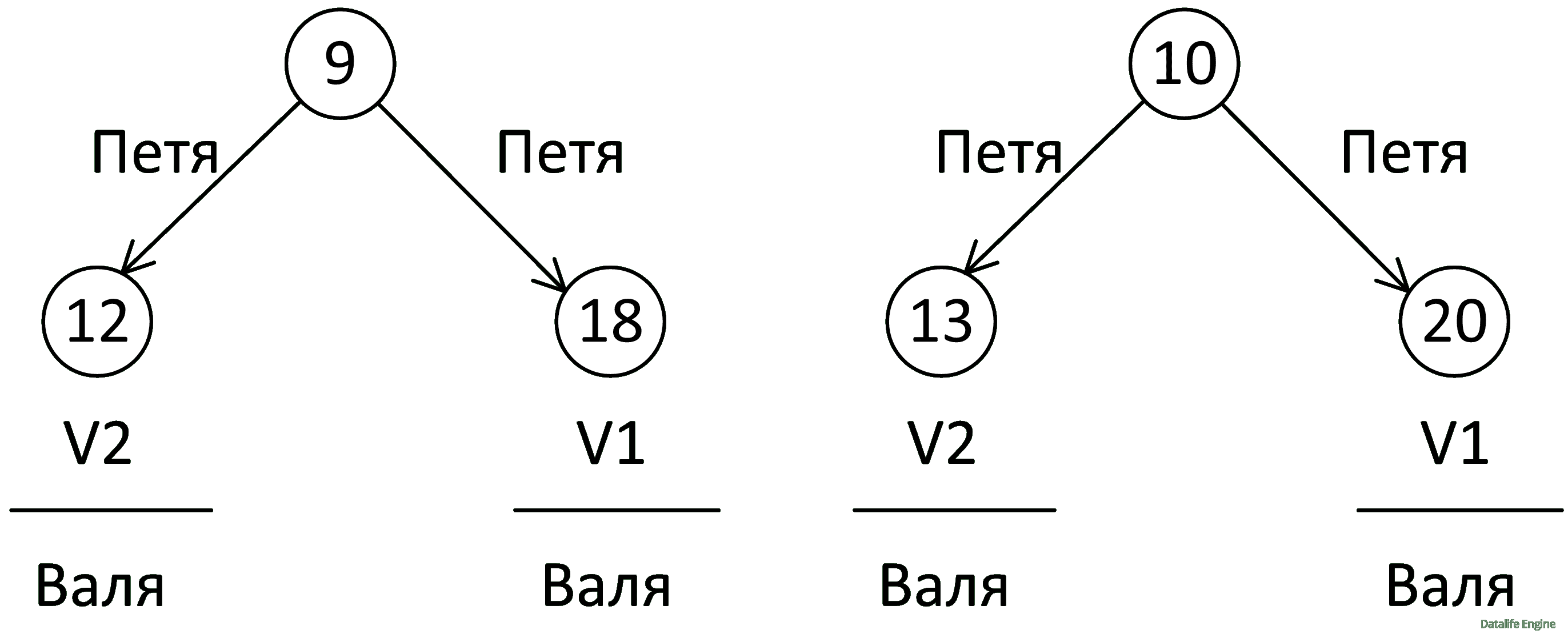
Ответ: 12, 18
Задача 3.3.3. Задание такое же, как и в предыдущей задаче. Ходы: +2, +3, *2.
Конец игры S ≤ 30. В начальный момент в куче было S камней: 1 ≤ S ≤ 29.
Я привел задачу с таким же заданием, что и в предыдущий раз, чтобы вы могли «набить руку». При достаточной тренированности таблица заполняется в течение пары минут:
|
14/2
|
|
|
max(+2,+3)=3
|
min(+2,+3)=2
|
30/2=15
|
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
…
|
29
|
|
V2
|
|
|
V2
|
V2
|
V2
|
X
|
X
|
V1
|
|
V1
|
Обратите внимание, что количество проигрышных позиций равно минимуму из операций сложения, то есть 2, а количество V2 идущих подряд, из которых с помощью сложения попадают в проигрышные позиции, равно максимуму из операций сложения, то есть 3.
Задача 3.3.4. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может (1) добавить в кучу один камень или (2) увеличить количество камней в куче в два раза или (3) увеличить количество камней в куче в три раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16, 30 или 45 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 36. Если при этом в куче оказалось не более 60 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче было 30 камней и Петя утроит количество камней в куче, то игра закончится и победителем будет Валя. В начальный момент в куче было S камней, 1 ≤ S ≤ 35.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит, описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при разной игре противника.
Выполните следующие задания.
1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.
б) У кого из игроков есть выигрышная стратегия при S = 31, 32, 33, 34? Опишите выигрышные стратегии для этих случаев.
2. У кого из игроков есть выигрышная стратегия при S = 11? Опишите соответствующие выигрышные стратегии.
3. У кого из игроков есть выигрышная стратегия при S = 10? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход, в узлах – количество камней в позиции.
Как и в предыдущей задаче, начните составлять таблицу с метками, кто выиграет.
Составим таблицу с метками выигрыша / проигрыша
|
10
|
11
|
12…17
|
18…30
|
31
|
32
|
33
|
34
|
35
|
|
V2
|
X
|
V1
|
V1
|
V1,2
|
X
|
V2
|
X
|
V1
|
|
+1=11
*2=20
*3=30
|
11+1=12(V1)
*2=22(V1)
*3=33(V2)
|
*3=36…51
|
*2=36…60
|
+1=32(X)
*2=62>60
*3=93>60
|
+1=33(V2)
*2=64>60
*3=96>60
|
+1=34(X)
|
+1=35(V1)
*2=68>60
*3=102>60
|
+1=36
|
Дерево решений предоставляем построить читателю самостоятельно.
Ответы:
1a. 12…30, 35
1б. 32,34 – Валя, 31, 32 – Петя
2. 11 – Валя
3. 10 - Петя
Задача 3.3.5. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, то есть этим ходом достигший 55 камней или более.
В начальный момент в первой куче было 5 камней, во второй 1 ≤ S ≤ 49
Задание 1. Укажите все значения S, при которых Петя может выиграть за один ход.
Задача представляет собой смесь задач 3.3.1 и 3.3.2. Поэтому старайтесь заполнять таблицу и там, где это необходимо, рисуйте дерево.
Найдем позиции V1 (выигрыша за 1 ход) (55 – 5) / 2 = 25:
Задание 2. Сколько существует значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом?
Рассмотрите большое значение во второй куче, но такое, которое не входит в V1.
Фактически речь идет о поиске проигрышной позиции. В прошлой задаче такой должна была быть предыдущая позиция (5, 24). Исследуем её:
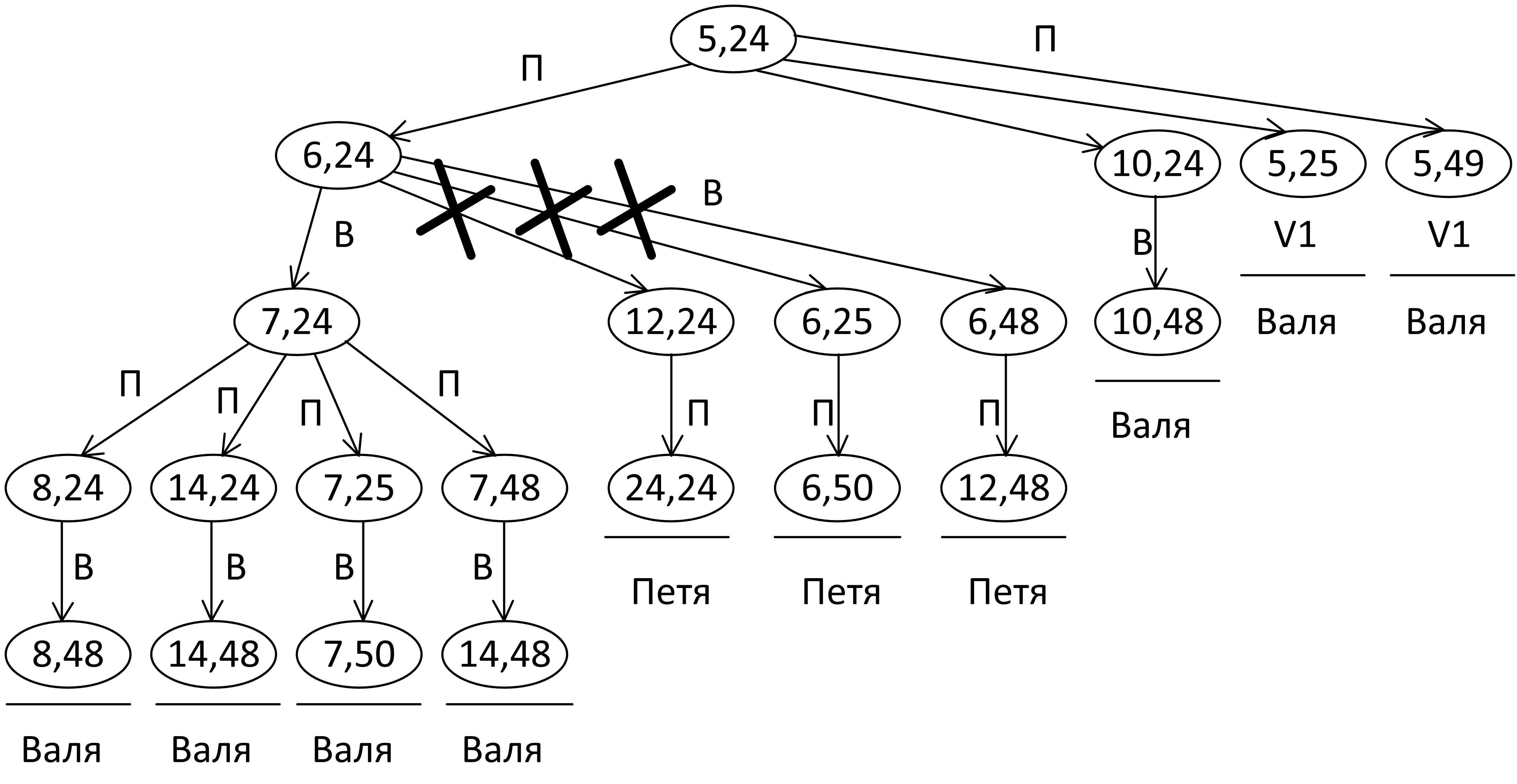
(5, 24) – это проигрышная позиция, но нет гарантии, что за один ход, возможно, за два. Значит, нет гарантии, что и в меньших позициях будет выигрыш за один ход. Следовательно, таких позиций нет.
|
5,25
|
5,25
|
…
|
5,49
|
|
X1,2
|
V1
|
|
V1
|
Ответ: 0
Задание 3. Укажите такое значение S, при котором одновременно выполняются два условия:
у Вали есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
у Вали нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Мы такое значение уже нашли – (5, 24). См. дерево в Задании 2. Там Валя выигрывает первым или вторым ходом в зависимости от игры Пети.
Задача 3.3.6. Два игрока, Петя и Валя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при разной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.
В этой задаче будет задано для изучения очень много позиций. Всякий раз надо думать, рисовать ли новое дерево или можно воспользоваться готовым из предыдущих заданий.
Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Построим дерево для начальной позиции (6, 33). Фактически это проигрышная позиция за следующий ход противника, поэтому пометим её X1 – может пригодиться при следующих заданиях.
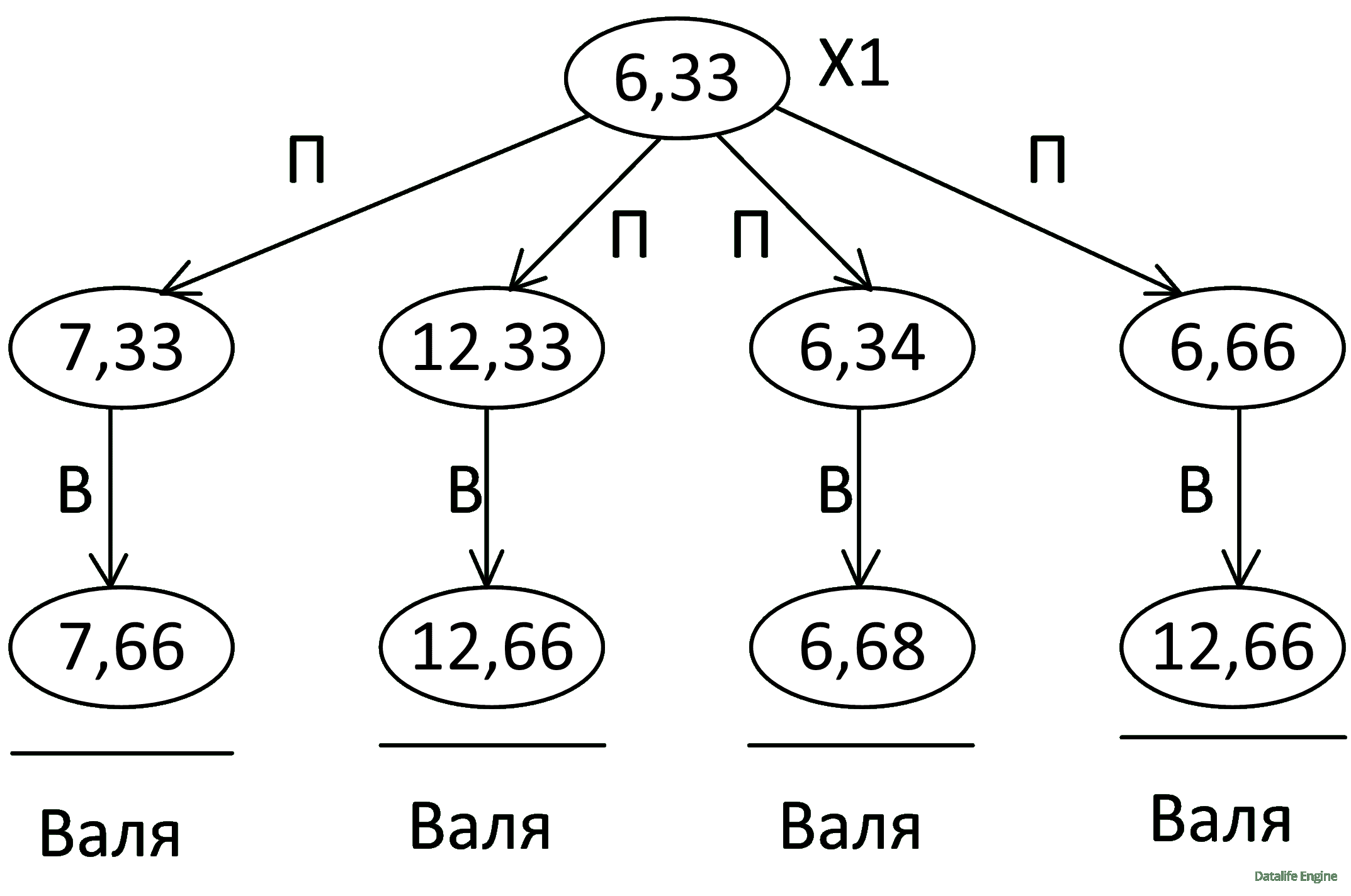
То же самое и для позиции (8, 32):
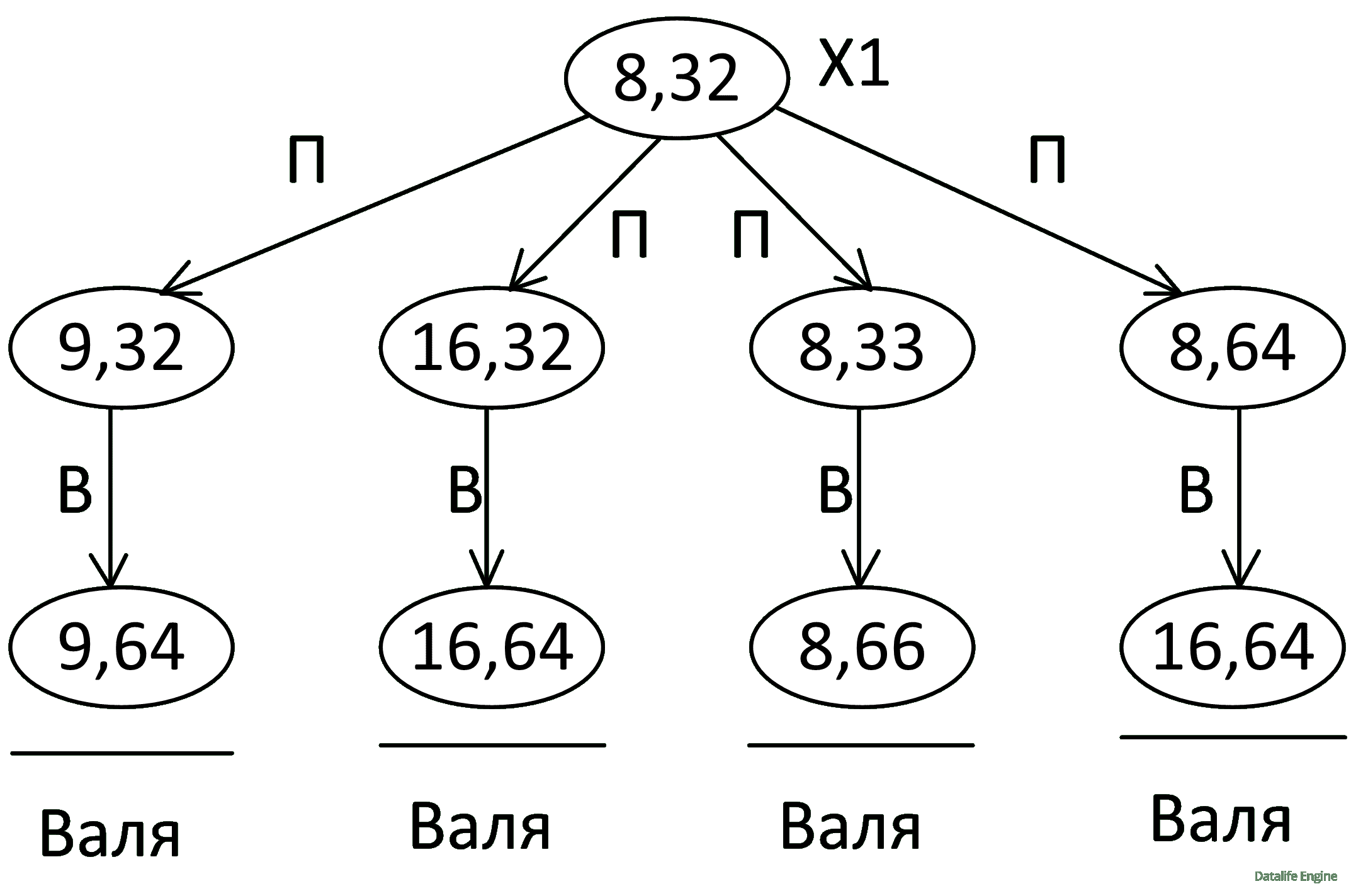
Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Не будем торопиться строить деревья решений, а воспользуемся проигрышными позициями из прошлого задания:
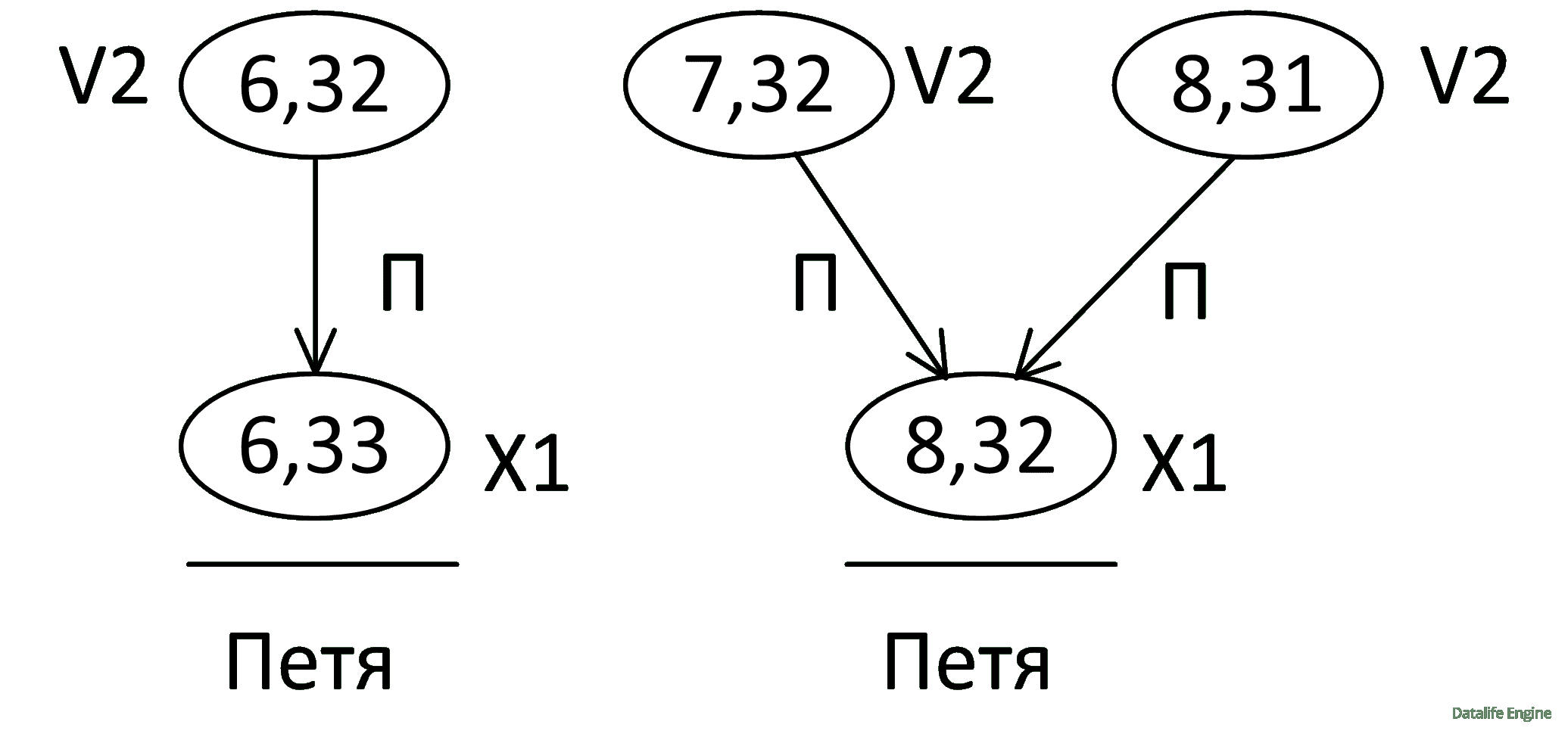
Эти позиции обеспечивают выигрыш за второй ход, так как Петя загоняет Валю в проигрышную позицию X1. Отметим начальные позиции в этом задании меткой V2.
Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
Для начала сведем позицию (7, 31) к изученным в предыдущем задании позициям:
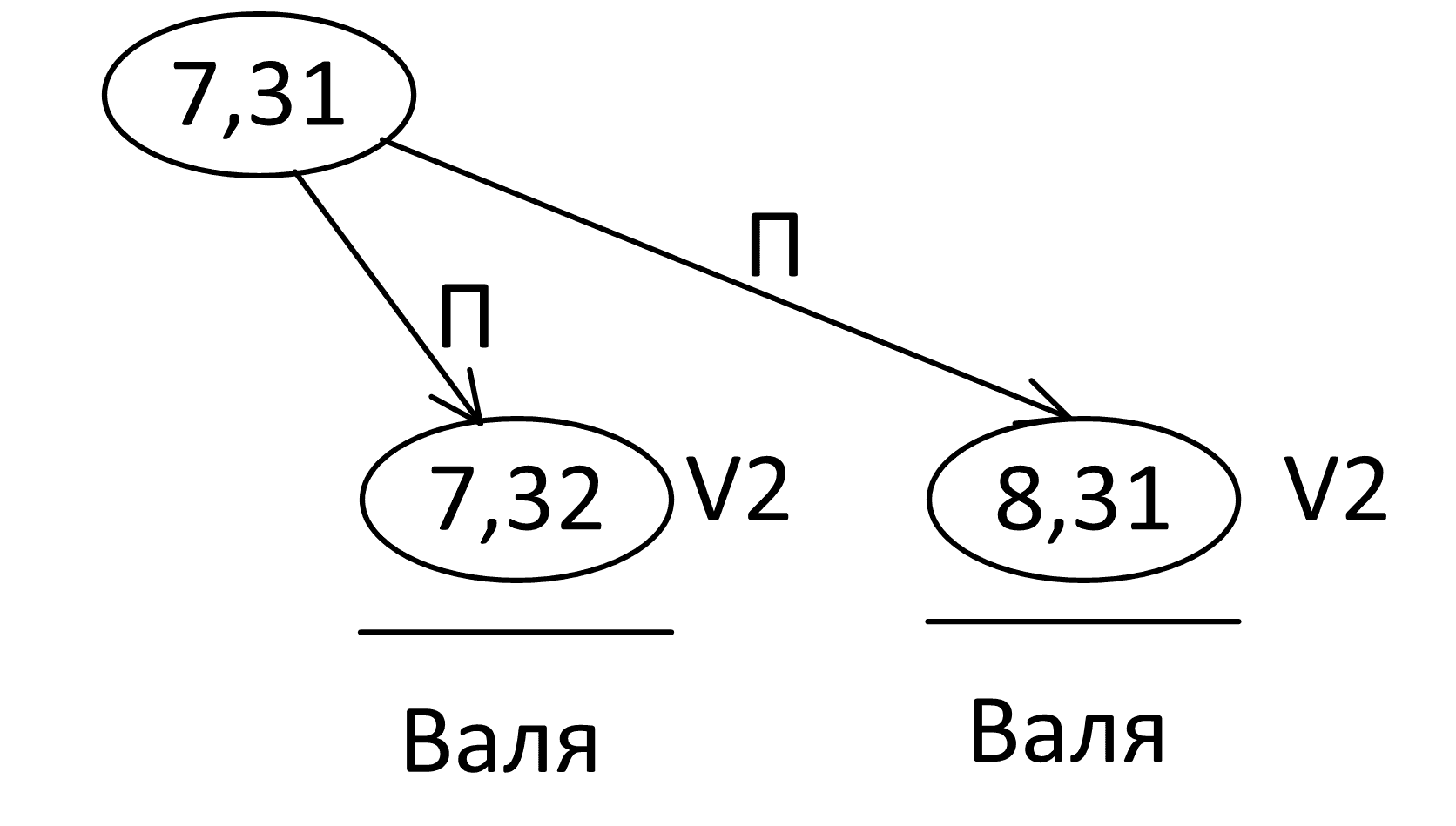
В них выигрывает Валя своим вторым ходом. Но если мы утверждаем, что Петя проиграет, мы должны изучить все его возможные ходы:
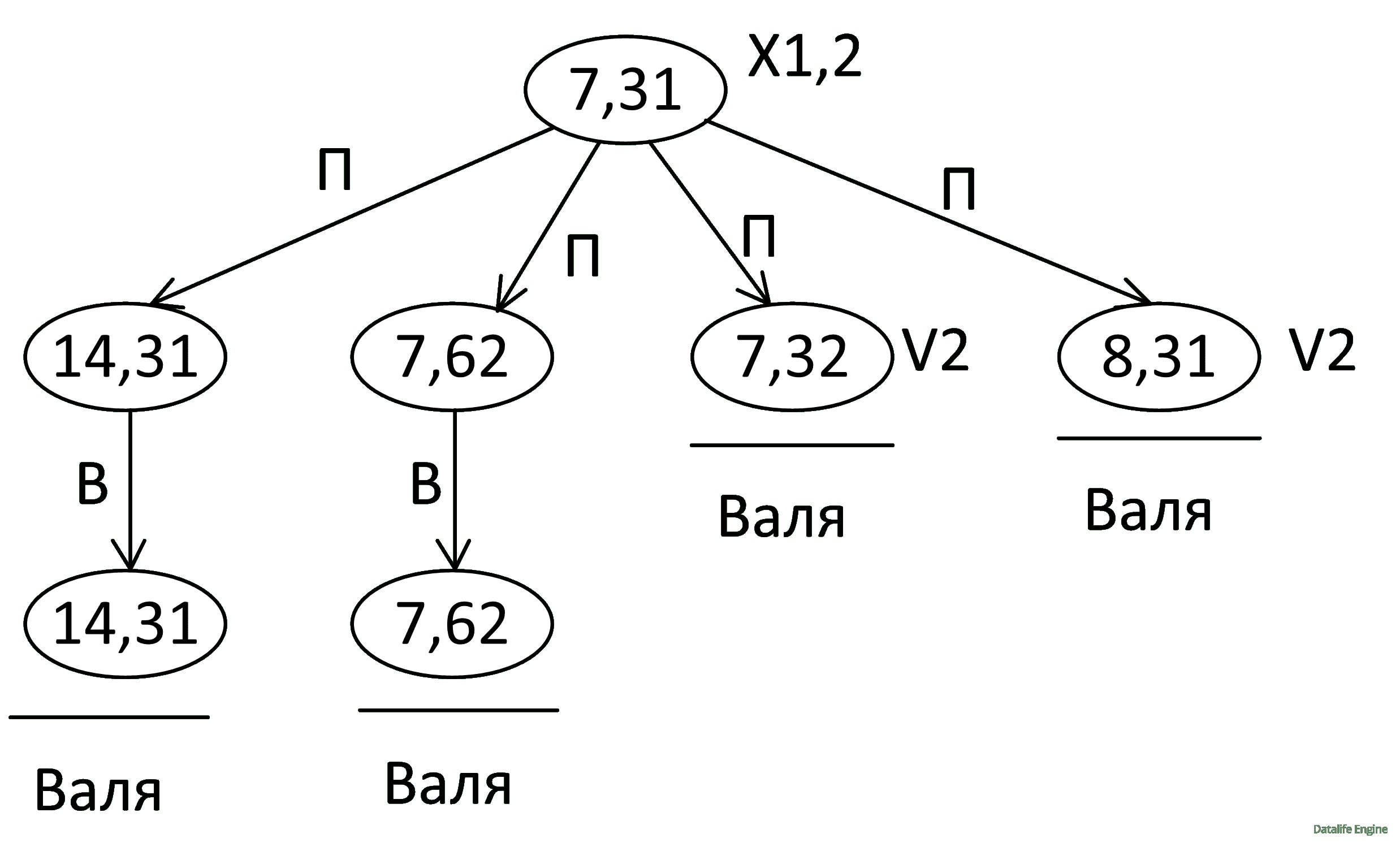
Получается, что Петя при любой игре Вали проиграет, а Валя выиграет за 1 или 2 хода в зависимости от игры Пети.
Мы изучили задачи, в которых графы и деревья – наилучший инструмент для их решения. Но этим их применение в ЕГЭ не ограничивается. Мы будем применять деревья при решении систем логических уравнений в следующей главе и в некоторых программистских задачах.



















