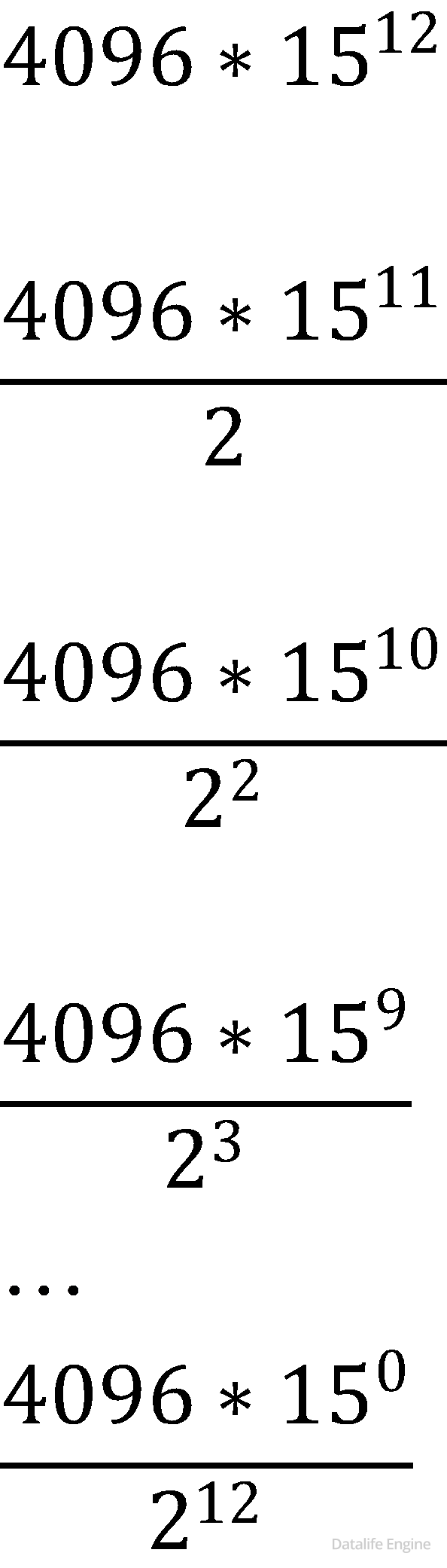Задача 3.2.1. Исполнитель может выполнять только две команды, которым присвоены номера:
- Прибавь 1
- Возведи во вторую степень
Напишите самую короткую программу, которая из числа 1 получает 37. Если таких программ несколько, напишите любую из них.
Дерево здесь не нужно. Начинайте решать с результата – числа 37, стараясь делать как можно больше операций извлечения квадратного корня (обратного действия для возведения во вторую степень).
37 = 36 + 1 = 62 + 1 = (5 + 1)2 + 1 = (4 + 1 + 1)2 + 1 = (22 + 1 + 1)2 + 1
= ((1 + 1)2 + 1 + 1)2 + 1
Заменим операторы сложения и умножения на номера команд Исполнителя и получим программу 121121
Ответ: 121121
Задача 3.2.2. У исполнителя «Троечник» две команды, которым присвоены номера:
1. прибавь 3,
2. умножь на 3.
Первая из этих команд увеличивает число на экране на 3, вторая умножает его на 3. Программа - это последовательность номеров команд. Например, 121 - это программа прибавь 3, умножь на 3, прибавь 3. Эта программа преобразует число 1 в число 15.
Запишите программу, которая преобразует число 6 в число 69 и содержит не более 5 команд. Если таких программ более одной, то запишите любую из них.
Как и предыдущую задачу, начните составлять выражение с последнего числа и умножения. В отличие от предыдущей задачи, к начальному числу дойти не получится, поэтому заменяйте последние операции умножения на сложение.
Начнем решать с конца:
69 = 23 * 3 = (20 + 3) * 3 = (17 + 3 + 3) * 3 = (14 + 3 + 3 + 3) * 3 = (11 + 3 + 3 + 3 + 3) * 3 = (7 + 3 + 3 + 3 + 3 + 3) * 3
Мы не дошли до числа 6, поэтому заменим умножение в начале наших рассуждений на сложение:
69 = 66 + 3 = 22 * 3 + 3 = (19 + 3) * 3 + 3 = (16 + 3 + 3) * 3 + 3 = (13 + 3 + 3 + 3) * 3 + 3 = (10 + 3 + 3 + 3 + 3) * 3 + 3 = (7 + 3 + 3 + 3 + 3 + 3) * 3 + 3
Мы опять не дошли до 6. Заменим умножение на сложение:
69 = 63 + 3 + 3 = 21 * 3 + 3 + 3 = 7 * 3 * 3 + 3 + 3
Заменим второе появившееся в ходе рассуждений умножение на сложение:
69 = 63 + 3 + 3 = 21 * 3 + 3 + 3 = (18 + 3) * 3 + 3 + 3 = (6 * 3 + 3) * 3 + 3 + 3
Мы дошли до 6 за пять действий.
Ответ: 21211
Примечание. В информатике и программировании решение задачи с возвратом на предыдущие шаги и корректировкой называется бэктрекингом. Это распространенный прием.
Задача 3.2.3. Исполнитель может выполнять только две команды, которым присвоены номера:
- Прибавь 1
- Умножь на 2
Сколько есть программ, которые число 1 преобразуют в число 21?
В отличие от предыдущей задачи, нам нужно не написать самую короткую программу, а посчитать количество возможных программ. Поэтому постройте дерево программ, в котором вершинами будут промежуточные результаты, обращая внимание на одинаковые участки (для одинаковых участков повторно рисовать веточки нет смысла).
Начнем строить дерево.
1 + 1 = 2
1 * 2 = 2
Поскольку для правой и левой веточки мы получили одинаковый результат, нам достаточно посчитать количество программ для левой ветки, а для правой результат будет таким же:

Уровень 3:
2 + 1 = 3
2 + 2 = 4
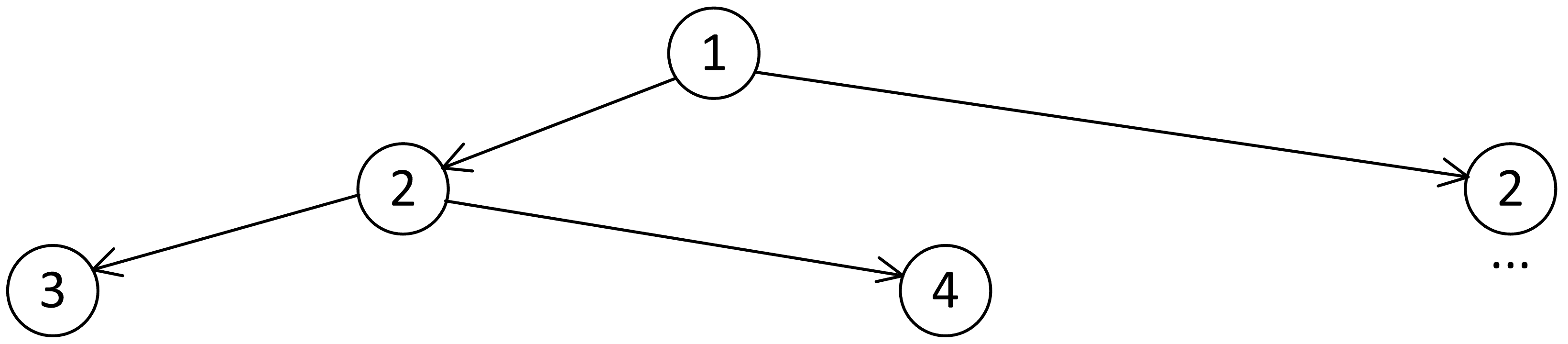
Уровень 4:
3 + 1 = 4 (четверку мы уже встречали, поэтому ставим многоточие)
3 * 2 = 6
4 + 1 = 5
4 * 2 = 8
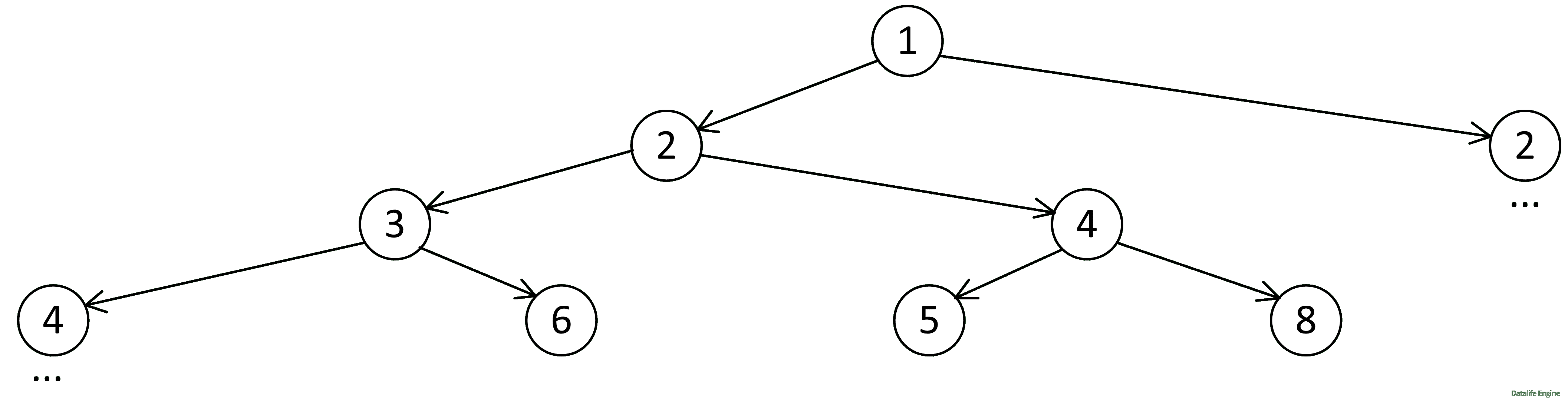
Уровень 5:
6 + 1 = 7
6 * 2 = 12 (далее программа не ветвится, так как 12 * 2 = 24 > 21, то есть программа представляет собой 12 + 1 + 1 + … + 1 = 21, поэтому подводим итог – по этой ветке идет одна программа)
5 + 1 = 6 (уже было)
5 * 2 = 10
8 + 1 = 9
8 * 2 = 16 (перестает ветвиться)
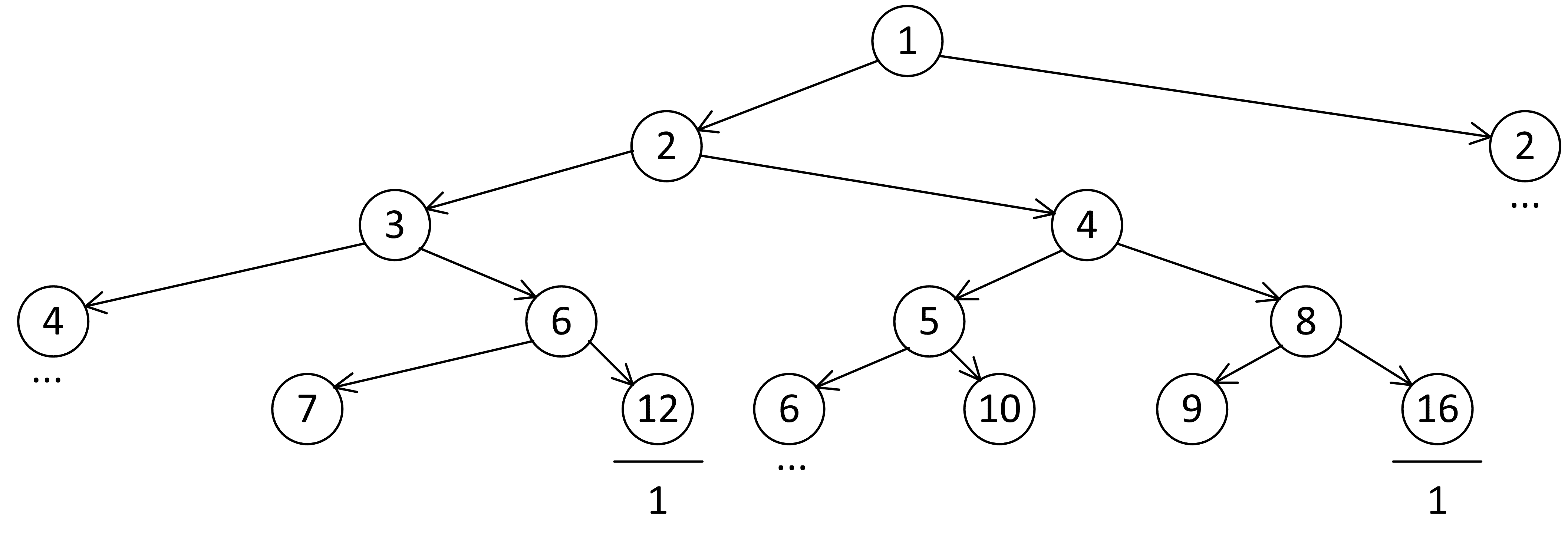
Уровень 6
7 + 1 = 8 (уже было)
7 * 2 = 14(перестает ветвиться)
10 + 1 = 11(перестает ветвиться)
10 * 2 = 20(перестает ветвиться)
9 + 1 = 10 (уже было)
9 * 2 = 18(перестает ветвиться)
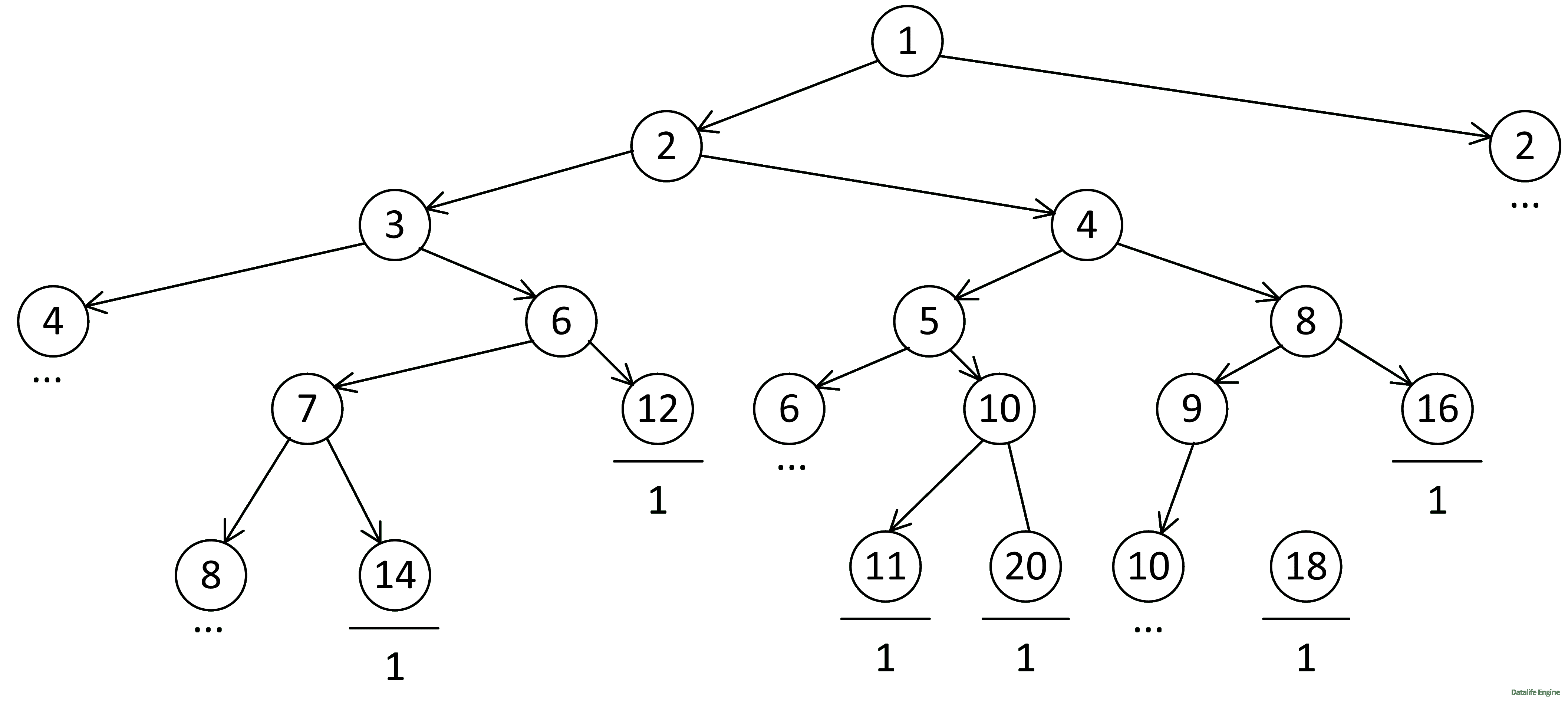
Как видите, несмотря на то, что, казалось бы, дерево должно быстро ветвиться, за счет одинаковых узлов оно получилось не такое уж и пышное. Теперь осталось посчитать количество веток там, где стоит многоточие. Проще всего начать с наибольшего числа – 10:
1 + 1 = 2
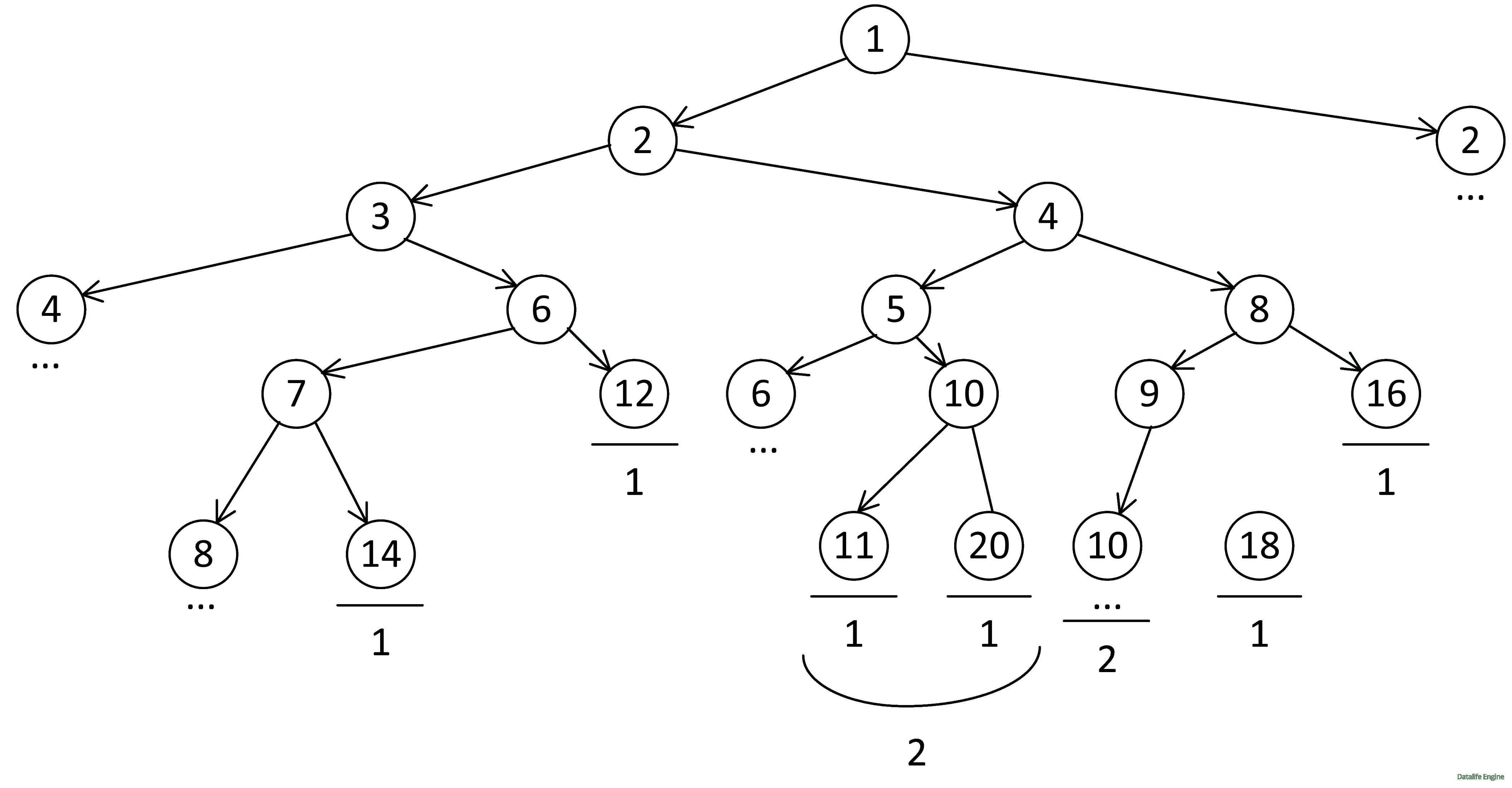
Затем для 8:
2 + 1 + 1 = 4
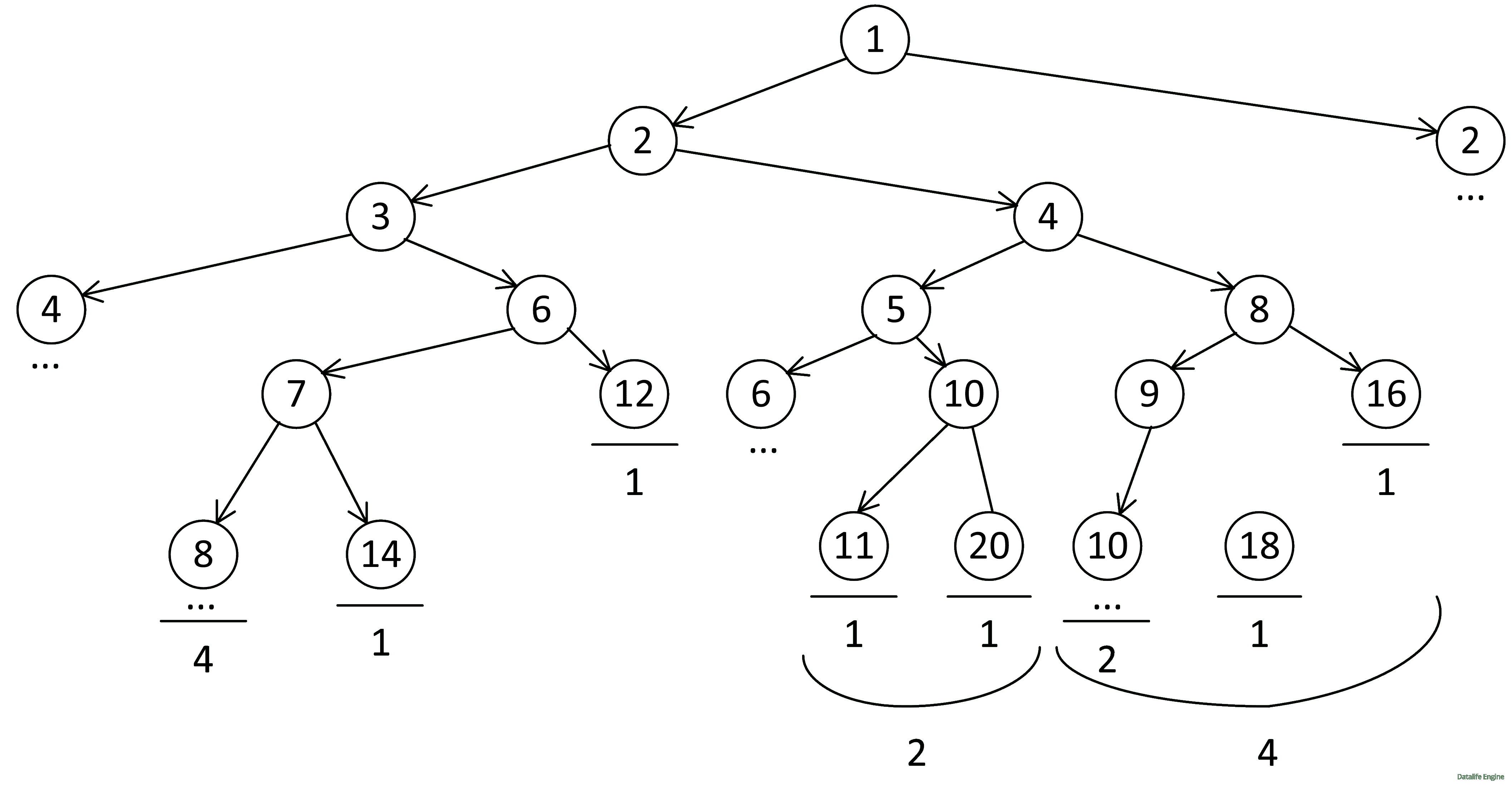
Для 6:
4 + 1 + 1 = 6
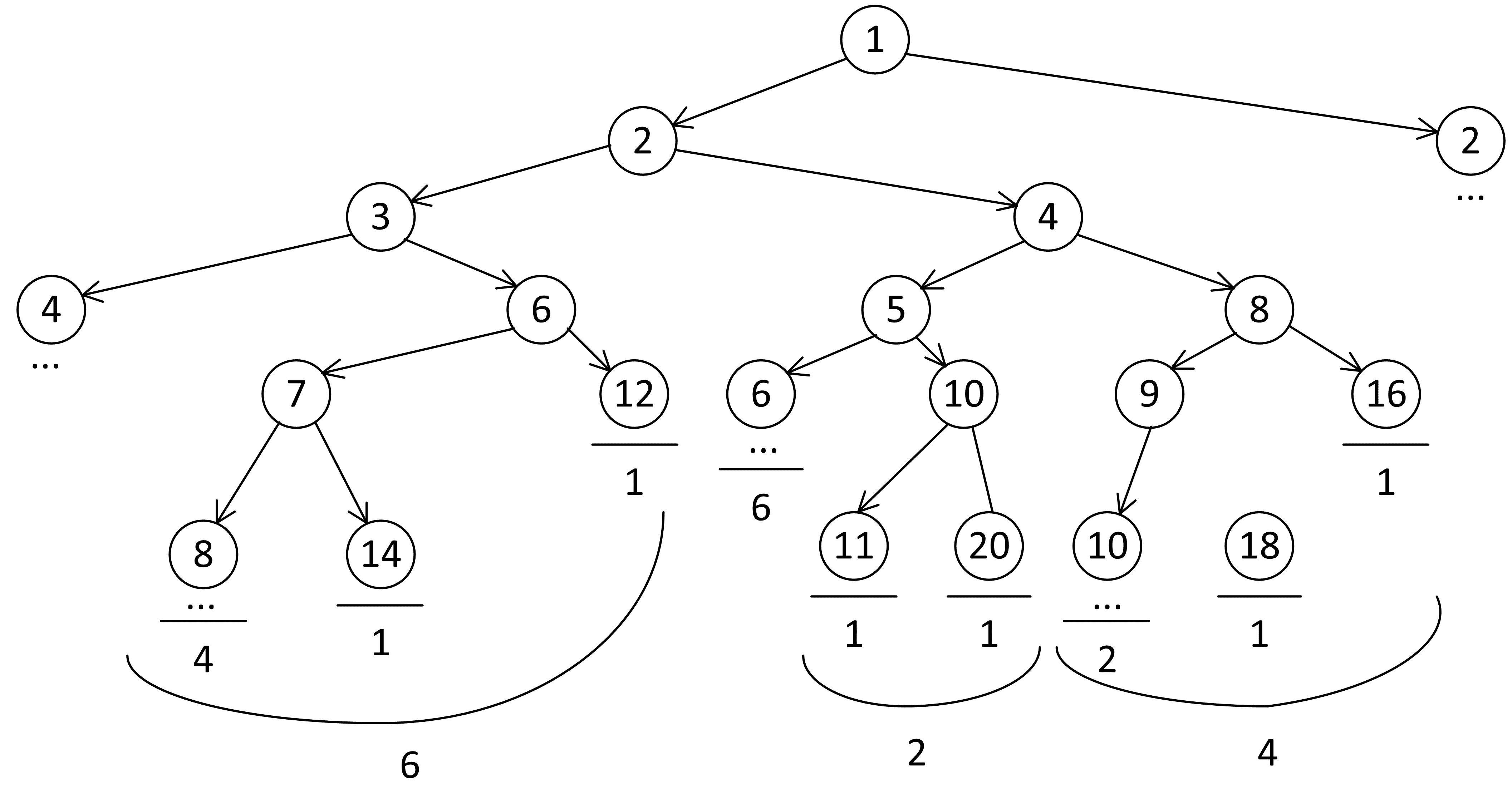
Для 4:
6 + 2 + 4 = 12
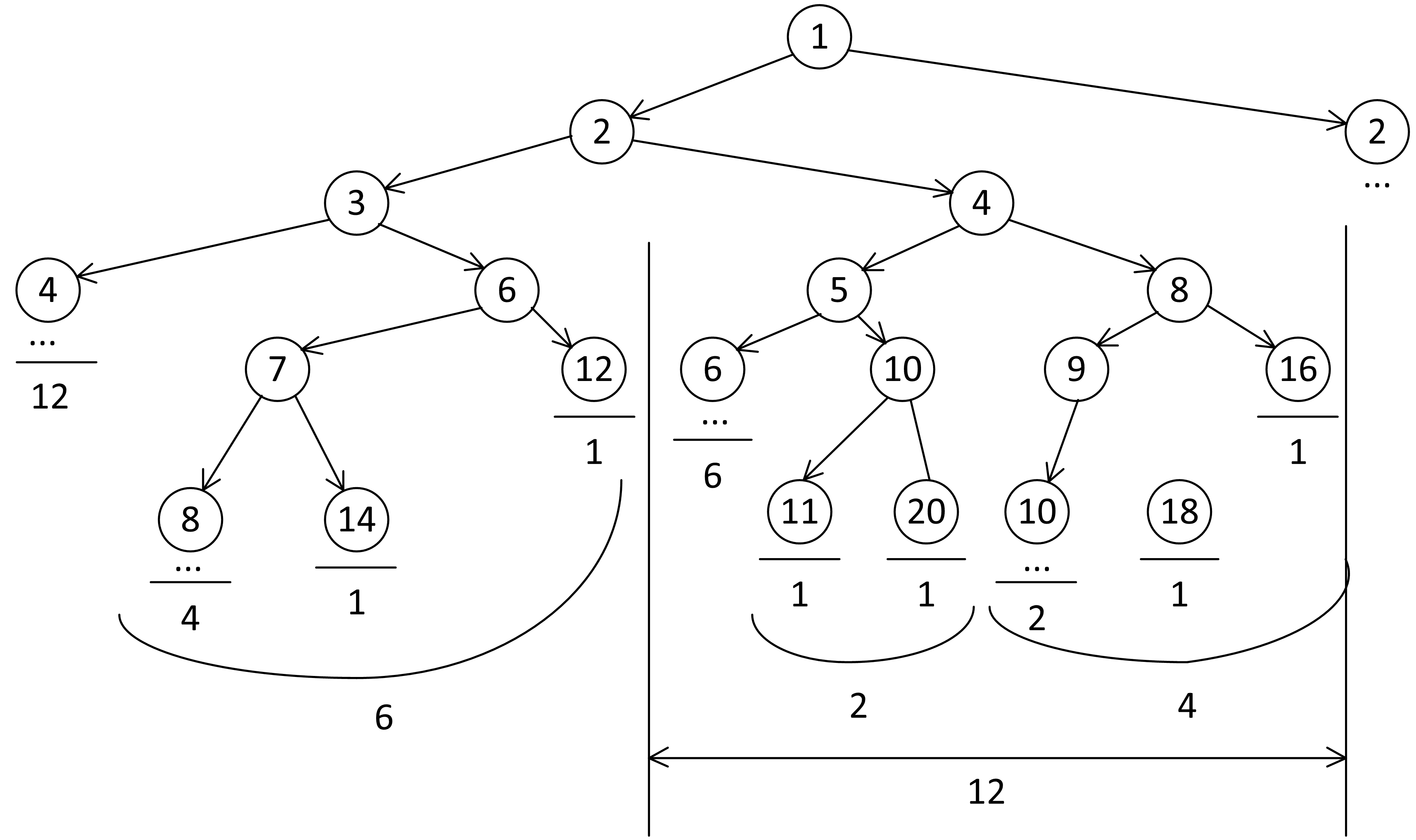
Для 3:
12 + 6 = 18
Для 2:
18 + 12 = 30
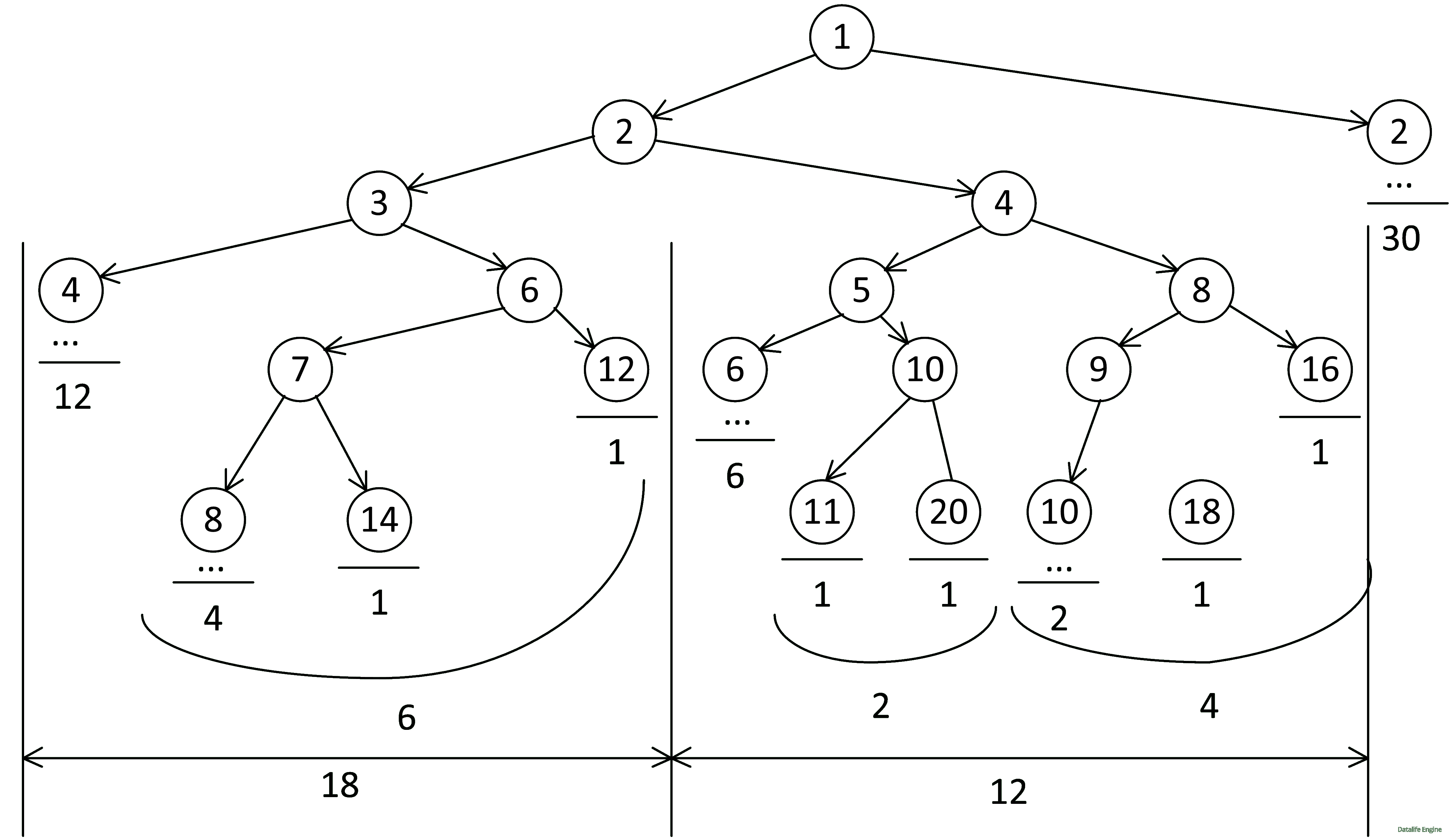
Всего: 30 + 30 = 60
Ответ: 60
Задача 3.2.4. Исполнитель может выполнять только две команды, которым присвоены номера:
- Прибавь 1
- Прибавь 2
Сколько различных чисел можно получить из числа 2 с помощью программы, которая содержит не более 4 команд?
В отличие от предыдущей задачи, нам не нужно определять количество различных программ, а нужно посчитать количество различных чисел. Следовательно, мы можем замыкать одинаковые веточки.
Ошибка 1. Строить дерево, как в предыдущей задаче, неверно, так как будет много ветвей и потом придется пересчитывать одинаковые числа в узлах.
Из числа 2 мы можем получить:
2 + 1 = 3
2 + 2 = 4
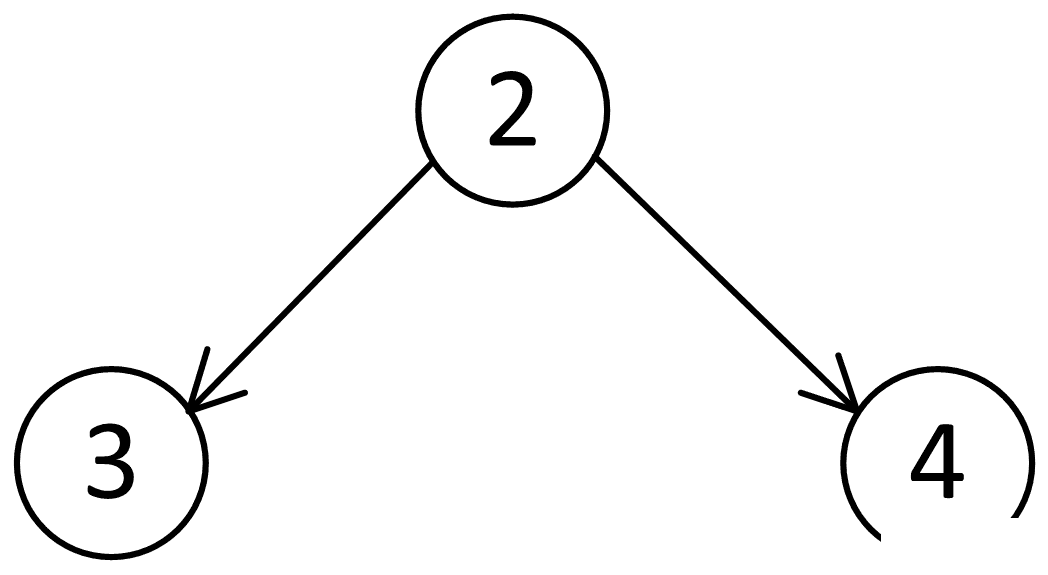
Команда 2:
3 + 1 = 4 (число уже было, поэтому замыкаем на него)
3 + 2 = 5
4 + 1 = 5 (число уже было, поэтому замыкаем на него)
4 + 2 = 6
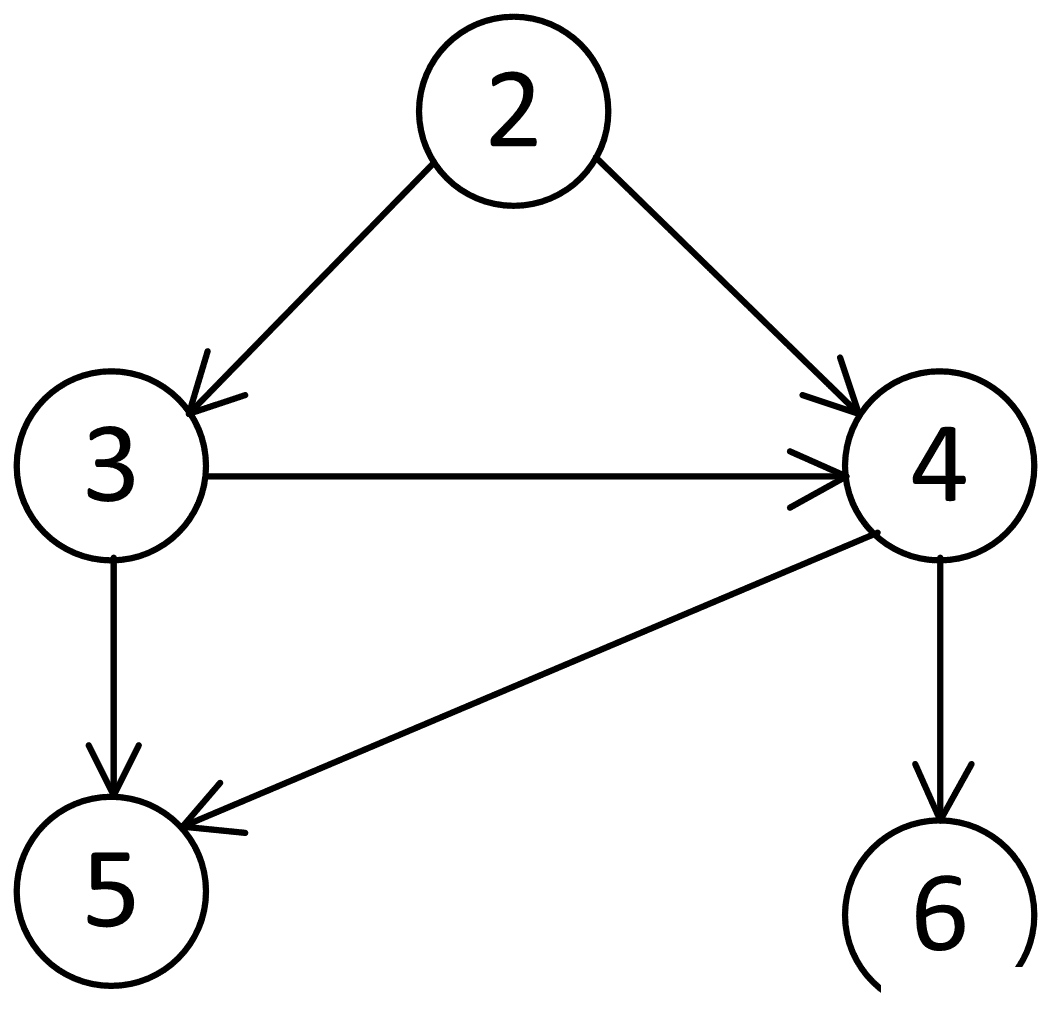
Команда 3:
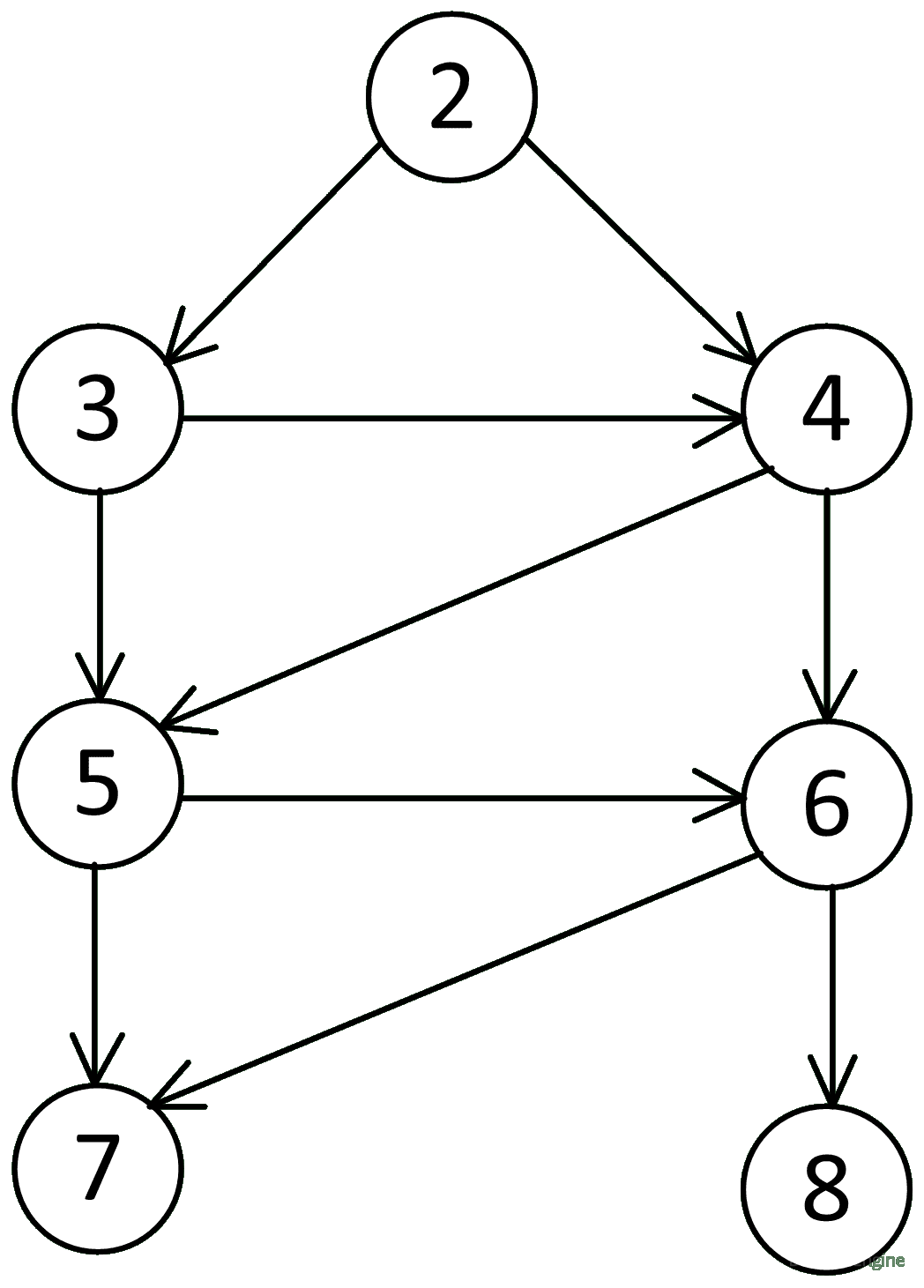
Команда 4:
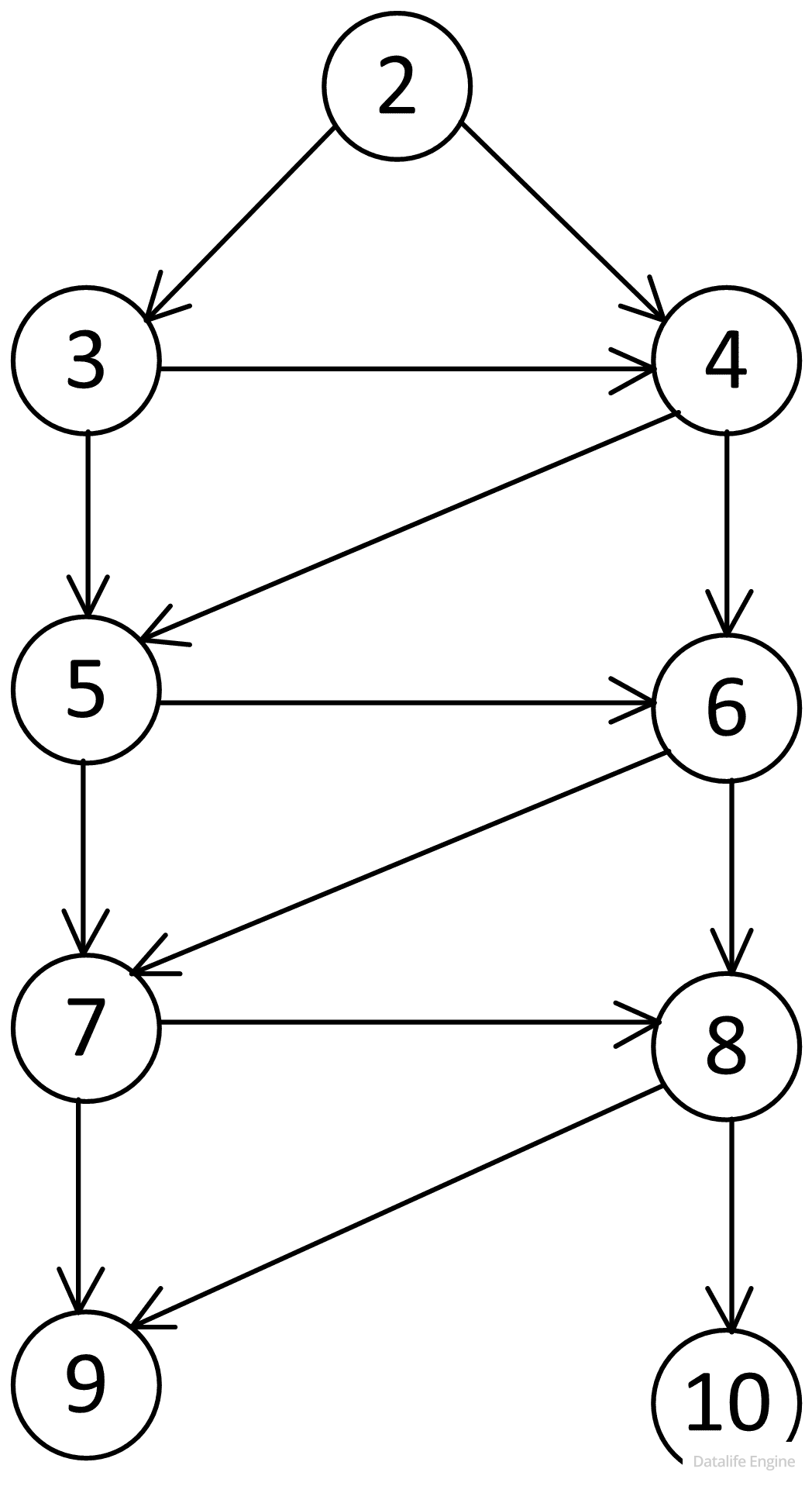
Количество различных чисел, которые можно получить из 2, равняется количеству узлов дерева, то есть 9.
Ошибка 2. Само число 2 тоже нужно сосчитать, так как пустая программа тоже считается программой.
Ответ: 9
Задача 3.2.5. Исполнитель может выполнять только две команды:
- Прибавь 3
- Вычти 2
Если в ходе вычислений появляется отрицательное число, то оно не выводится. Сколько различных чисел можно получить из числа 2 с помощью программ, которые содержат ровно 18 команд?
Ошибка. Строить дерево, даже как в предыдущей задаче, неверно, так как на 18 уровне оно будет сильно разветвленным.
Задача решается вообще без дерева. Промежуточные уровни нас не интересуют. Найдите сперва максимально возможное число, затем число перед ним и т.д.
Самое большое число можно получить, прибавляя три 18 раз:
2 + 3 * 18 = 56
Перед ним идет число, в котором 3 прибавляется 17 раз и один раз вычитается 2:
2 + 3 * 17 – 2 = 51
Перед ним идет число, в котором 3 прибавляется 16 раз и 2 раза вычитается 2:
2 + 3 * 16 – 2 * 2 = 46
Перед ним идет число, в котором 3 прибавляется 15 раз и 3 раза вычитается 2:
2 + 3 * 15 – 2 * 3 = 41
Заметьте, что новые числа меньше предыдущих на 5.
Дальше пойдут числа: 36, 31, 26, 21, 16, 11, 6, 1
Всего чисел 12.
Задача может быть усложнена тем, что таких чисел может получиться очень много. Поэтому хорошо было бы уметь находить их количество, не прибегая к вычислениям.
Пусть n – количество прибавлений 3, тогда 18 – n – количество вычитаний 2
n ≤ 18
Полученное число равняется:
2 + 3 * n – 2 * (18 – n)
Оно неотрицательно:
2 + 3 * n – 2 * (18 – n) ≥ 0
2 + 3 * n – 36 + 2 * n ≥ 0
5 * n ≥ 34
6, 8 ≤ n ≤ 18
То есть n принимает значения от 7 до 18 включительно, поэтому всего таких чисел
18 – 7 + 1 = 12
Ошибка. Можно посчитать как 18 – 7 = 11. Такая ошибка уже встречалась нам в предыдущих задачах. Можете проверить на малых последовательностях чисел и убедиться, что в нестрогих неравенствах нужно прибавлять единицу, а в строгих – вычитать.
Ответ: 12
Задача 3.2.6. У исполнителя Калькулятор две команды:
1. умножь на 15,
2. подели на 2.
Первая из них увеличивает число на экране в 15 раз, вторая – уменьшает его в 2 раза. Программа для Калькулятора – это последовательность команд. Сколько различных чисел можно получить из числа 4096 с помощью программы, которая содержит ровно 12 команд?
Как в прошлой задаче, перечислим числа, только не будем их вычислять:
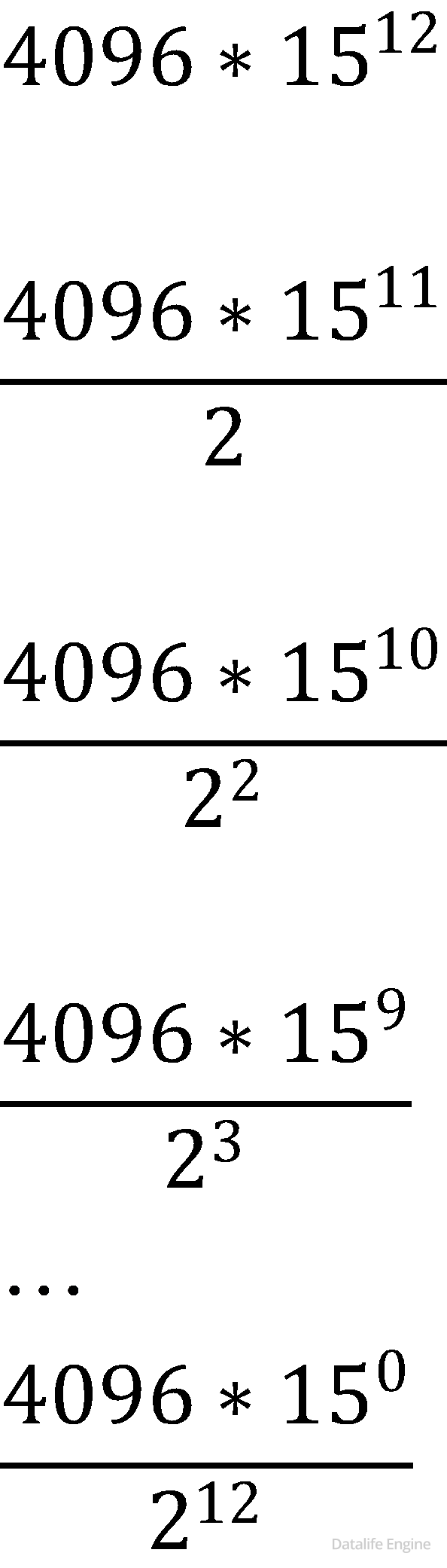
…
Чтобы пересчитать эти числа, посмотрим на степени при числе 15:
0, 1, 2, …, 12. Всего таких чисел – 13.
Ответ: 13
Задача 3.2.7. У исполнителя Калькулятор две команды:
1. прибавь 2
2. прибавь 3.
Первая из них увеличивает число на экране на 2, вторая — на 3. Сколько различных чисел можно получить из числа 2 с помощью программы, которая содержит ровно 10 команд?
Самое большое число: 2 + 3 * 10 = 32
Следующее перед ним: 2 + 3 * 9 + 2 = 31
Далее: 2 + 3 * 8 + 2 * 2 = 30
Видно, что числа отличаются друг от друга на 1.
Найдем самое маленькое число: 2 + 2 * 10 = 22.
Наши числа лежат в диапазоне от 22 до 32. Так как границы включены, их количество 32 – 22 + 1 = 11.
Ответ: 11
Задача 3.2.8. Исполнитель может выполнять только три команды:
- Прибавь 2
- Прибавь 4
- Прибавь 5
Сколько есть программ, которые число 31 преобразуют в число 51?
Можно начать строить дерево, как в задаче 3.2.2. Но, поскольку у нас нет команды «прибавь 2», многие ветки могут оказаться тупиковыми - с их помощью не получить числа 51. Поэтому целесообразно применить знания комбинаторики (из задачи 2.2.4): составить программу, состоящую из одних «+2», потом заменять две «+2» на одну «+4» и менять расположение «+4», подсчитывая количество расположений, и т.д.
1) Первая программа:
31 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 =51.
Для краткости запишем её как:
Это 1 программа
2) Заменим две двойки на 4:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
4
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
Расположение четверки имеет значение:
422222222
и
242222222
- это разные программы.
Таких перемещений одной четверки 9, следовательно, количество подобных программ – 9
3) Заменим еще одну двойку на одну четверку:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
4
|
4
|
2
|
2
|
2
|
2
|
2
|
2
|
Количество возможных расположений двух 4 равно:
7 + 6 + 5 + 4 + 3 + 2 + 1 = 28
Следовательно, подобных программ – 28
(Если вы забыли, как это считается, то повторите задачу 2.2.4)
4) Заменим еще одну двойку на одну четверку:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
4
|
4
|
4
|
2
|
2
|
2
|
2
|
Количество возможных расположений двух 4 равно:
(5 + 4 + 3 + 2 + 1) + (4 + 3 + 2 + 1) + (3 + 2 + 1) + (2 + 1) + 1 = 35
Следовательно, подобных программ – 35
5) Заменим еще одну двойку на одну четверку:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
4
|
4
|
4
|
4
|
2
|
2
|
Количество возможных расположений двух 4 равно:
5 + 4 + 3 + 2 + 1 = 15
Следовательно, подобных программ – 15
6) Заменим еще одну двойку на одну четверку:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
4
|
4
|
4
|
4
|
4
|
Подобных программ всего 1
7) Одну пятерку вместить в программу не получится, нужны сразу две:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
5
|
5
|
2
|
2
|
2
|
2
|
2
|
|
|
|
|
|
|
|
|
|
|
|
Таких расположений 5 всего 6 + 5 + 4 + 3 + 2 + 1 = 21
8) Заменим две двойки на 4:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
5
|
5
|
4
|
2
|
2
|
2
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим сначала расположение двух пятерок не зависимо от расположения двоек и четверки:
Таких расположений 5 + 4 + 3 + 2 + 1 = 15
В каждом из таких расположений находятся 4 ячейки, в которых помещается одна четверка и три двойки:
То есть 4 расположения
Значит, всего вариантов программ в этом случае 15 * 4 = 60
9) Заменим еще две двойки на 4:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
5
|
5
|
4
|
4
|
2
|
|
|
|
|
|
|
|
|
|
|
|
Расположений пятерок вне зависимости от двойки и четверок:
4 + 3 + 2 + 1 = 10
В каждом из этих случаев расположений двойки и четверок:
То есть 3 расположения
Всего вариантов программ в этом случае 10 * 3 = 30
10) Наконец, последняя программа:
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
5
|
5
|
5
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
Сложим результаты всех случаев и получим количество программ:
1 + 9 + 28 + 35 + 15 + 1 + 21 + 60 + 30 + 1 = 201
Ответ: 201
Задача 3.2.9. Исполнитель Фибо преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2.
Программа для исполнителя Фибо — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 20, и при этом траектория вычислений содержит число 9 и не содержит числа 15?
Траектория вычислений — это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 7 траектория будет состоять из чисел 9, 10, 12.
Деревья решений, комбинаторика
Так как все программы проходят через 9, построим дерево программ от 3 до 9:
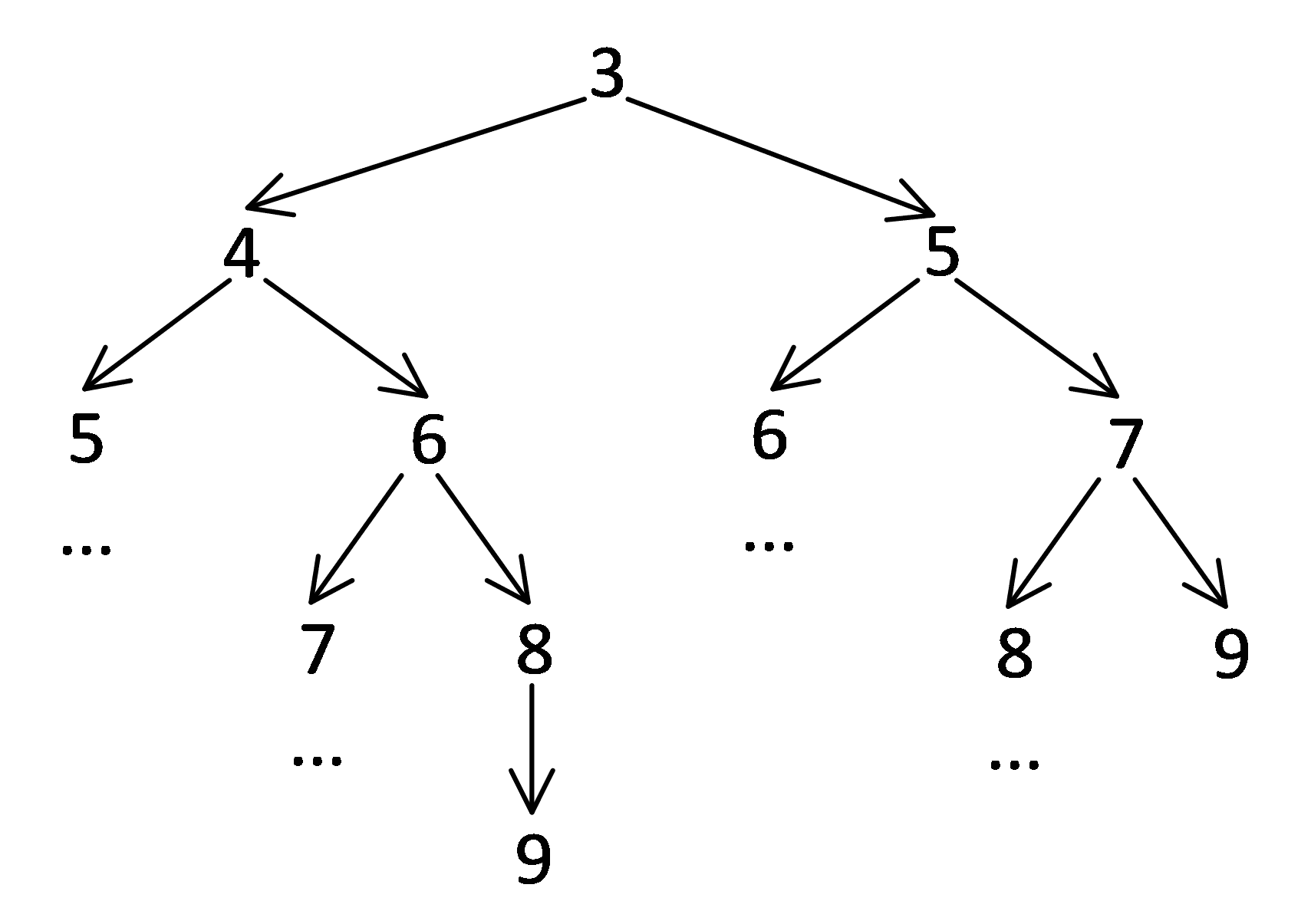
Посчитаем количество программ:
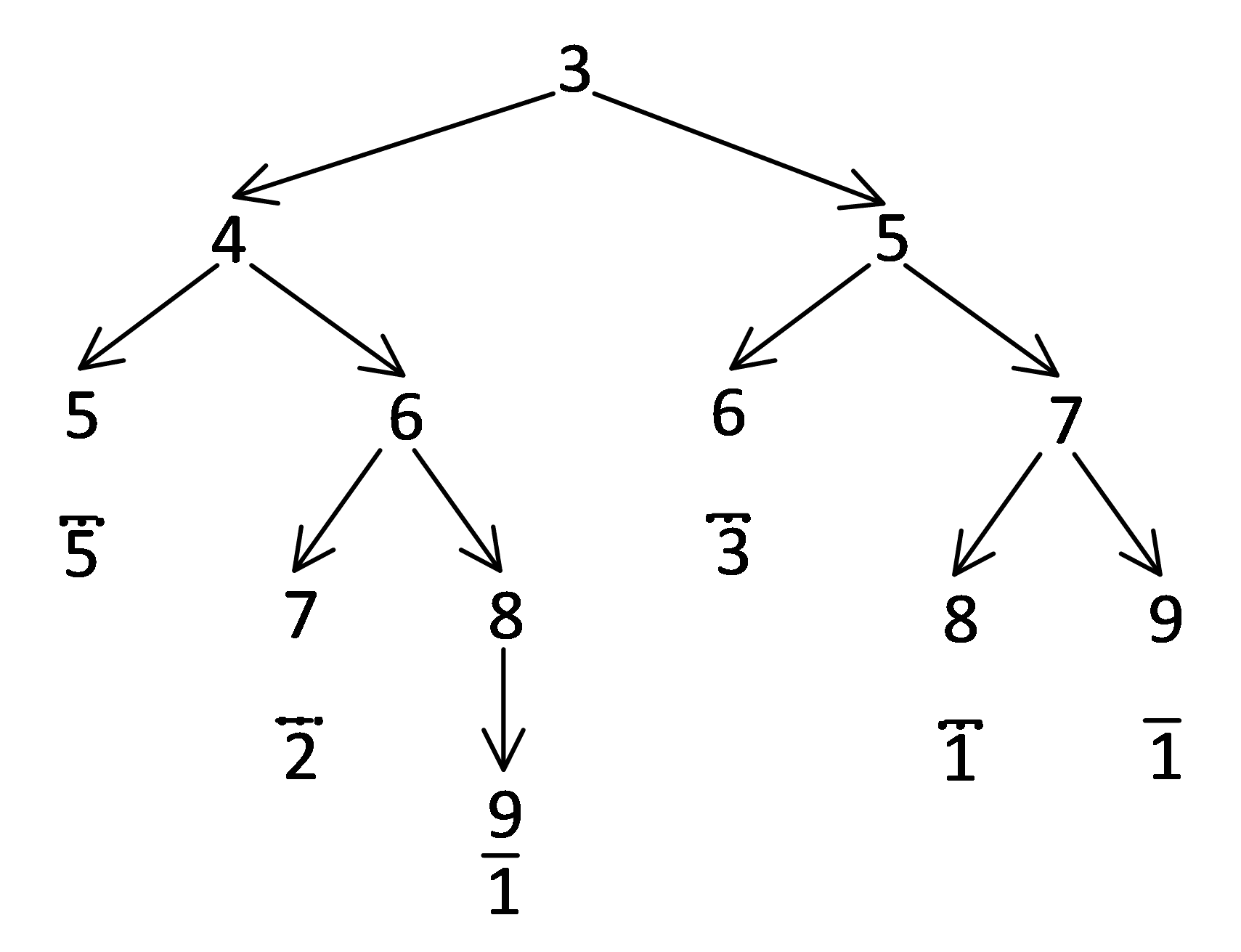
Количество программ, преобразующих 3 в 9, равно 13.
Начнем строить дерево от 9:
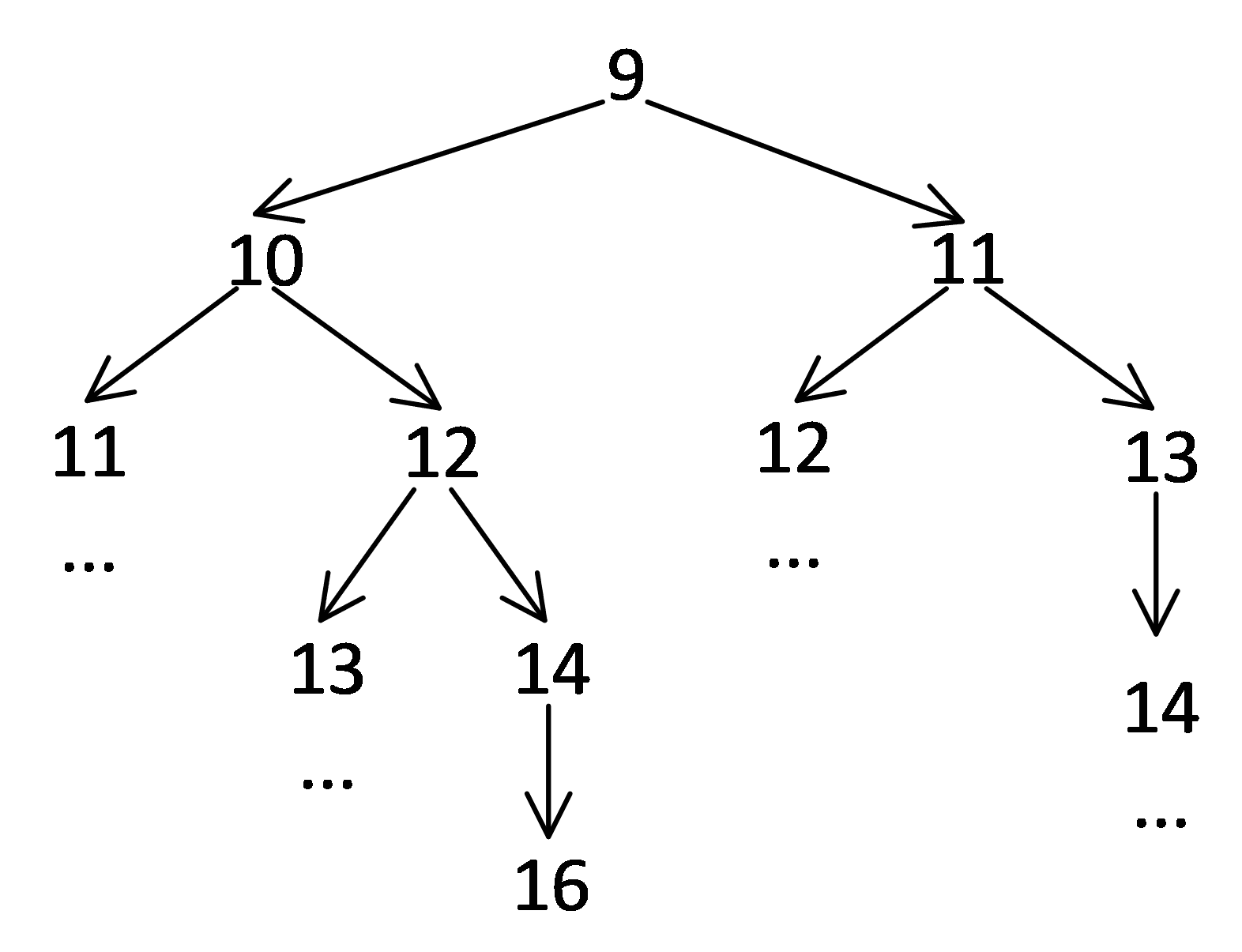
Поскольку траектории программ не должны проходить через 15, видно, что все они проходят через 16. Посчитаем количество программ от 9 до 16:
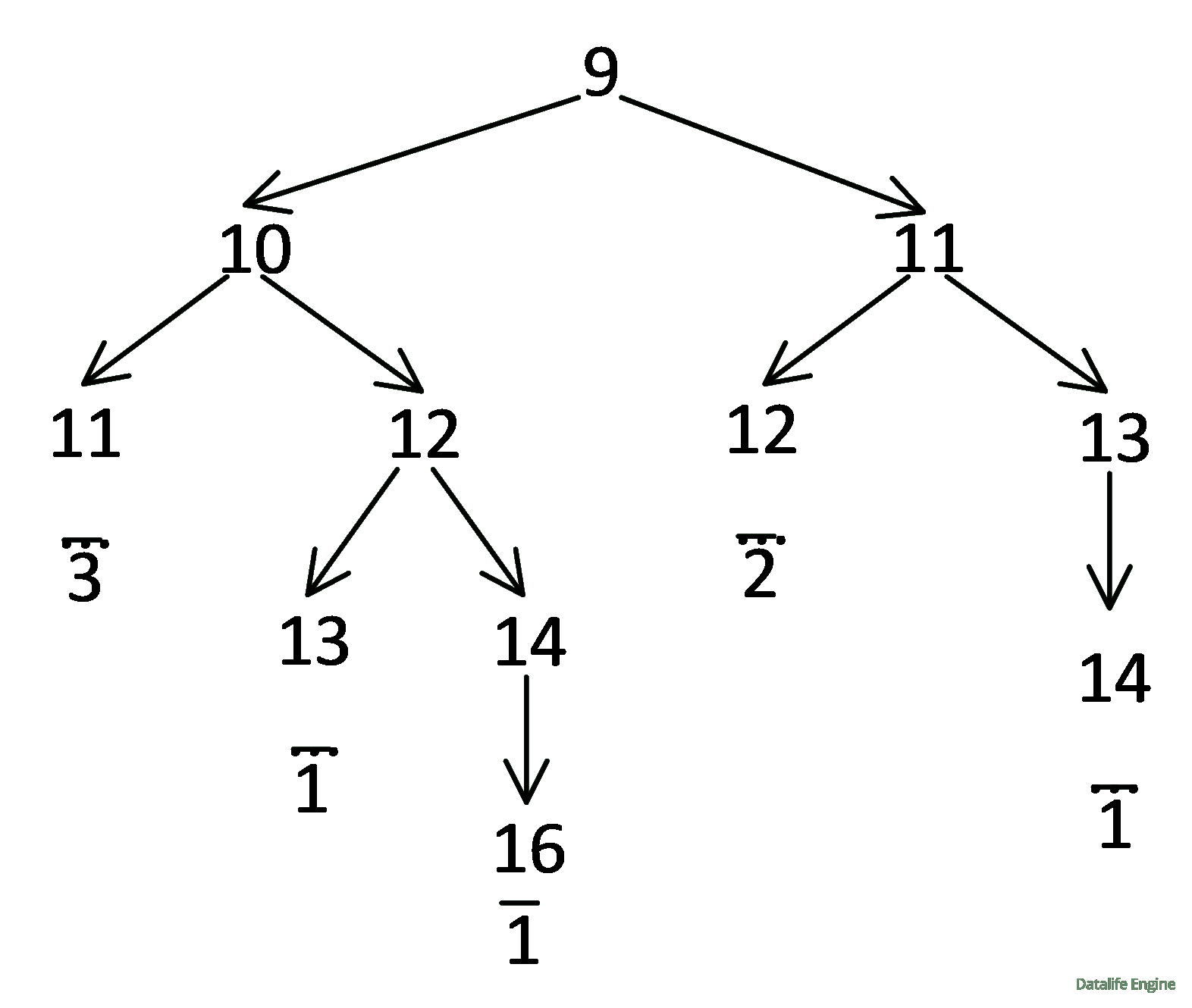
Количество программ, преобразующих 9 в 16, равно 8.
Построим дерево траекторий программ от 16 до 20
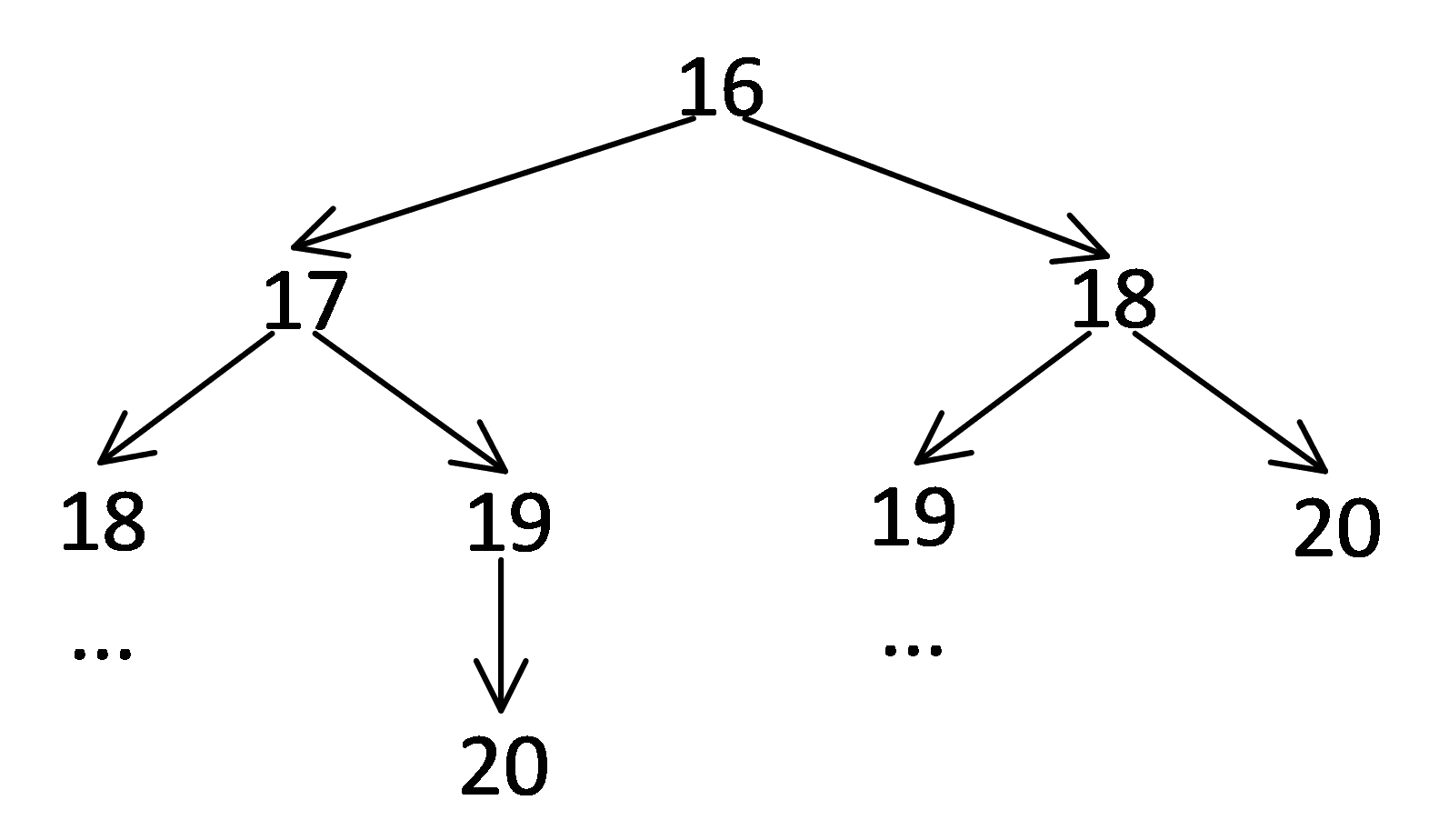
Посчитаем количество программ от 16 до 20:
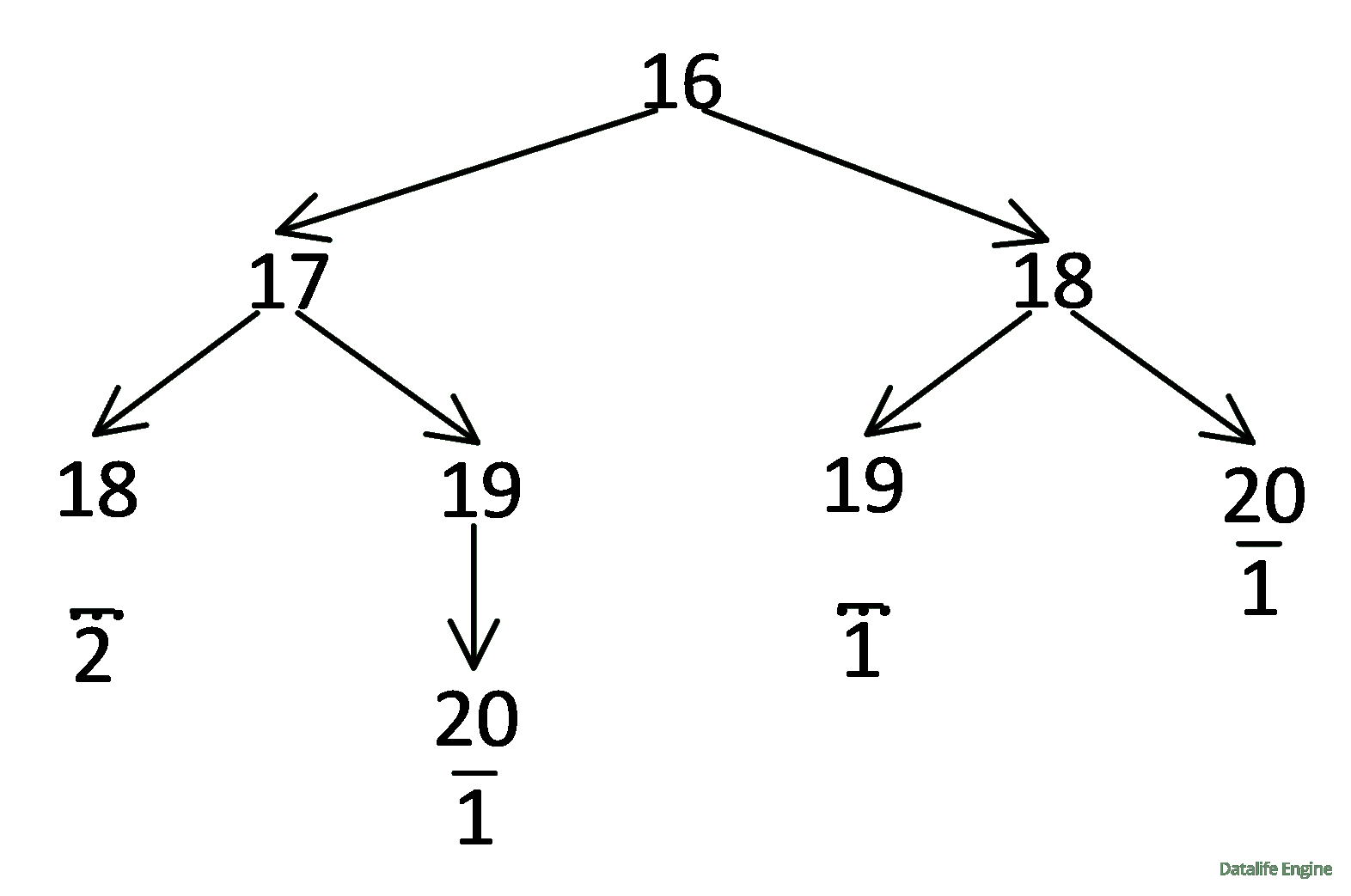
Количество программ, преобразующих 9 в 16, равно 5.
Осталось соединить количества программ от 3 до 9, от 9 до 16 и от 16 до 20. Пользуемся знаниями комбинаторики и получаем 13 * 8 * 5 = 520.
Рекурсия + комбинаторика
Решим задачу без построения деревьев. С рекурсией мы уже встречались в комбинаторных задачах, когда располагали три буквы по n клеткам и подсчитывали количество таких расположений. Здесь более простой пример рекурсии.
Если мы внимательно посмотрим на деревья из предыдущего хода решения, то мы увидим, что количество программ до n вычисляется по формуле:
R(n) = R(n –1) + R(n – 2)
(так как у нас два действия: +1 и +2, то в n мы можем попасть из позиций n –1 и n – 2, следовательно, чтобы получить количество программ R(n), нужно сложить количество программ R(n –1) и R(n – 2)).
Начнем обсчет:
R(3) = 1 (количество программ из 3 в 3 – это одна программа, пустая).
R(4) = 1 (количество программ из 3 в 4 – это одна программа: 3 + 1 = 4)
R(5) = R(3) + R(4) = 1 + 1 = 2 (количество программ в 5 – это две программы: 3 + 2 = 5 и 4 + 1 = 5)
R(6) = R(4) + R(5) = 1+2 = 3 (мы можем получить 6 из 4 и 5. Из 5 у нас две программы, из 4 – одна, всего - 3).
R(7) = R(5) + R(6) = 2 + 3 = 5
R(8) = R(6) + R(7) = 3 + 5 = 8
R(9) = R(7) + R(8) = 5 + 8 = 13
Аналогично посчитаем количество программ из 9 до 16:
R(9) = 1
R(10) =1
R(11) = R(9) + R(10) = 1 + 1 = 2
R(12) = R(10) + R(11) = 1 + 2 = 3
R(13) = R(11) + R(12) = 2 + 3 = 5
R(14) = R(12) + R(13) = 3 + 5 = 8
R(16) = R(14), так как 15 пропускаем.
Аналогично посчитаем количество программ из 16 до 20:
R(16) = 1
R(17) = 1
R(18) = R(16) + R(17) = 1 + 1 = 2
R(19) = R(17) + R(18) = 1 + 2 = 3
R(20) = R(18) + R(19) = 2 + 3 = 5
Пользуемся знаниями комбинаторики и получаем 13 * 8 * 5 = 520.
Заметим, что при старте от 3, 9 и 16 получается один и тот же ряд.
Ряд, в котором первые два числа равны 1, а каждое следующее равно сумме двух предыдущих, называется числами Фибоначчи: 1 1 2 3 5 8 13 21 34 55 … . Это очень распространенный математический ряд, часто встречающийся на практике и в задачах ЕГЭ.
Следовательно, мы можем вычислить этот ряд один раз:
|
Позиция
|
Кол-во решений:
|
|
3
|
1
|
|
4
|
1
|
|
5
|
2
|
|
6
|
3
|
|
7
|
5
|
|
8
|
8
|
|
9
|
13
|
А затем просто переписать начальные позиции:
|
Старт с 3:
|
Кол-во решений:
|
Старт с 9:
|
Старт с 16:
|
|
3
|
1
|
9
|
16
|
|
4
|
1
|
10
|
17
|
|
5
|
2
|
11
|
18
|
|
6
|
3
|
12
|
19
|
|
7
|
5
|
13
|
20
|
|
8
|
8
|
14
|
|
|
9
|
13
|
|
|
Ответ: 520
Примечание.
На рекурсию есть отдельная задача в ЕГЭ под номером 11.