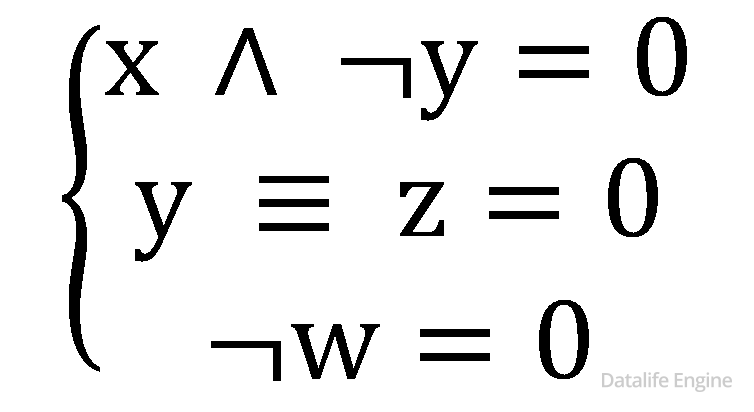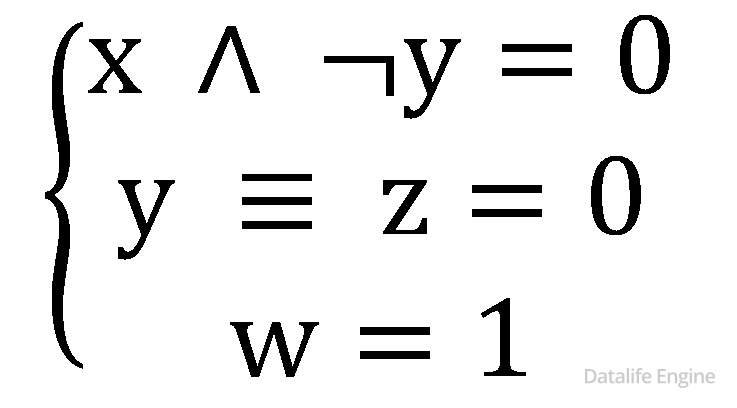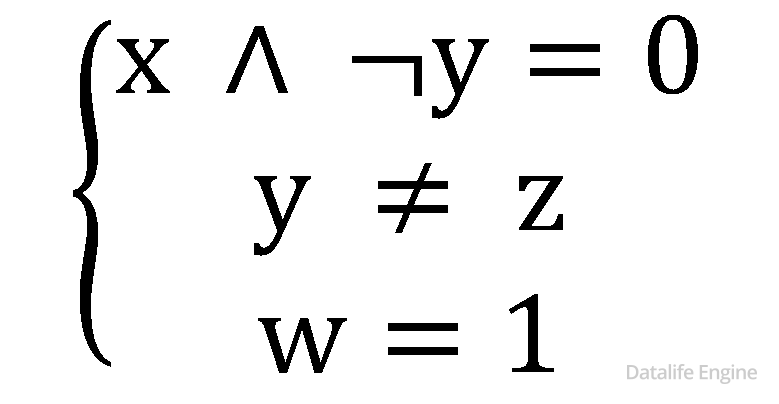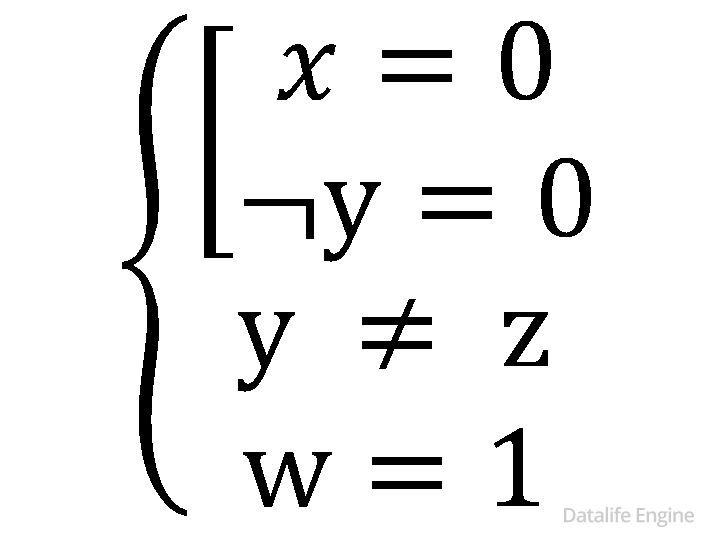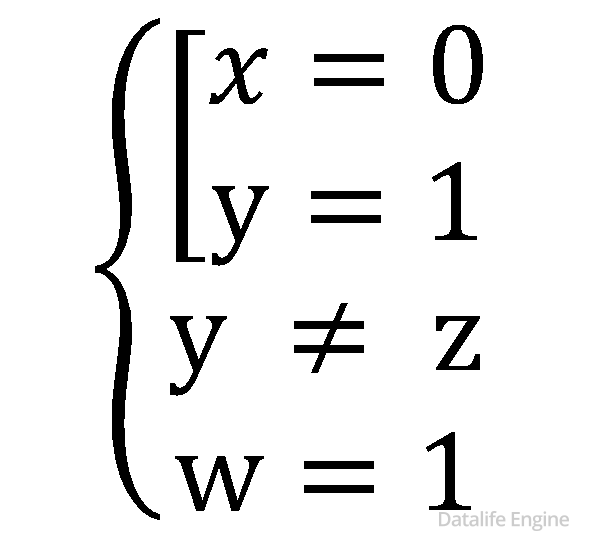Образовательный портал Павла Добряка

Эту задачу можно решить и не зная никакой теории, исходя из здравого смысла и понимания союза «И».

Союз «И» означает, что все условия должны выполняться:

1. Люксембург – первая буква согласная, третья буква согласная, последняя гласной не является. Неверно.
2. Бельгия – первая и третья буквы согласные, последняя – гласная. Подходит
3. Австрия – первая буква гласная. Неверно
4. Греция – первая буква согласная, третья – гласная. Неверно.

Ответ: 2

Формальный путь – подставлять каждую строчку из таблицы истинности в каждую формулу и проверять точное соответствие F. Можно и упростить выражения

Упростим выражения. Из таблиц истинности следует, что:

0 ∧ Y = 0

1 ∧ Y = Y

0 ∨ ⌐Z = ⌐Z

⌐1 ∧ Y = 0 ∧ Y = 0

Выражения приобретают вид:

1) 0 ∧ (X ≡ Z)
2) Y ∧ (X ≡ Z)
3) ⌐Z ∧ (X ≡ Y)
4) 0 ∧ (X ≡ Z)

Продолжаем упрощать:

1) 0
2) Y ∧ (X ≡ Z)
3) ⌐Z ∧ (X ≡ Y)
4) 0

Таким образом, 1 и 4 формулы не годятся, так как они тождественно равны 0, то есть принимают значение 0 при любых значениях операндов.

 

Посчитаем значение формулы 2

X	Y	Z	Y ∧ (X ≡ Z)	F
1	0	0	0	0
0	1	0	1	1
0	0	1	0	0

Она равна F

 

Посчитаем значение формулы 3

X	Y	Z	⌐Z ∧ (X ≡ Y)	F
1	0	0	0	0
0	1	0	0	1
0	0	1	0	0

Она не равна F

Ответ: 2

Так же, как и в арифметике, в логике существуют формулы для упрощения выражений. Но их мы пока не знаем. Поэтому составьте таблицу истинности и посмотрите, что получится.

X	Y	X   Y	⌐Х	⌐Х ∧ Y	⌐(⌐Х ∧ Y)	Всё выражение
0	0	1	1	0	1	1
0	1	1	1	1	0	0
1	0	0	0	0	1	0
1	1	1	0	0	1	1

 

А теперь посмотрите на таблицы истинности. Что это за операция? A ≡ B

 

Теория. Теперь изучим формулы для упрощения выражений:

Первые две формулы учатся легко и называются законами де Моргана:

⌐(A ∧ B) = ⌐A ∨ ⌐B

⌐ (A ∨  B) = ⌐A ∧ ⌐B

При раскрытии скобок с общим отрицанием, отрицание становится у каждого операнда, а логическое действие «переворачивается» - «и» заменяется на «или» и наоборот.

Третью формулу запомнить тяжелее всего, но она больше всех применяется в ЕГЭ, поэтому запомнить надо:
 A → B = ⌐A ∨ B

Четвертая формула менее распространена:

(A → B) ∧ (B → A) = A ≡ B

Вспомним, что у A ≡ B есть еще одно обозначение A ↔ B.

Теперь понятно, откуда оно происходит?

(A → B) ∧ (B → A) = A ↔ B

Если мы попробуем прочитать это выражение по-русски, то получится:

Если А, то B и если B, то A

А, если и только если B или А, тогда и только тогда, когда  B

Упростим выражение по формулам:

(X → Y) ∧ ¬ (¬X ∧ Y) =

(X → Y) ∧ (¬(¬X) ∨ ¬Y) =

(X → Y) ∧ (X ∨ ¬Y) =

(X → Y) ∧ (¬Y ∨ X) =

(X → Y) ∧ (Y → X) =

A ≡ B

 

Ответ: A ≡ B

Изучим первую формулу:

¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7 ∧ x8 ∧ x9 ∧ x10

И подставим значение первой строчки:

X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	результат
0	1	0	1	1	1	0	1	1	1
¬x1 ∧	x2 ∧	¬x3 ∧	x4 ∧	x5 ∧	x6 ∧	¬x7 ∧	x8 ∧	x9 ∧	x10
1 ∧	1 ∧	1 ∧	1 ∧	1 ∧	1 ∧	1 ∧	1 ∧	1 ∧	1	1

 

Подставим значение второй строчки:

X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	результат
1	0	1	1	0	0	1	1	1	0
¬x1 ∧	x2 ∧	¬x3 ∧	x4 ∧	x5 ∧	x6 ∧	¬x7 ∧	x8 ∧	x9 ∧	x10
1 ∧	0 ∧	Дальше можно не смотреть…								0

 

Подставим значение второй строчки:

X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	результат
0	1	0	1	0	1	0	0	1	0
¬x1 ∧	x2 ∧	¬x3 ∧	x4 ∧	x5 ∧	x6 ∧	¬x7 ∧	x8 ∧	x9 ∧	x10
1 ∧	1 ∧	1 ∧	1 ∧	0 ∧	Дальше можно не смотреть…					0

 

Полученные значения совпадают с F, поэтому первая формула подходит под фрагмент таблицы истинности. Следующие формулы можно не смотреть. Чтобы попрактиковаться, предлагаем читателю исследовать их.

Ответ: 1

Как и в предыдущих задачах, подставляйте в формулу значения из таблицы. Подвох задачи заключается в том, что, поскольку в таблице есть пустые клетки, то в них может быть как 0, так и 1, следовательно, в результате возможна как 0, так и 1.

Изучим первую формулу.

Подставим значения первой строчки:

x1 ∧ ¬x2 ∧ x3 ∧ ¬1 ∧ x5 ∧ 0 ∧ ¬x7 ∧ ¬x8 = 0,

а в таблице истинности F=1.

 

Проверим вторую формулу:

Подставим первую строку таблицы истинности:

¬x1 ∧ x2 ∧ ¬x3 ∧ 1 ∧ x5 ∧ 0 ∧ x7 ∧ ¬x8 = 0,

а в таблице истинности F=1.

 

Проверим третью формулу:

Подставим первую строку таблицы истинности:

x1 ∨ x2 ∨ ¬x3 ∨ 1 ∨ x5 ∨ ¬0 ∨ x7 ∨ x8 = 1,

Совпадает с F из таблицы истинности

Подставим вторую строку таблицы истинности:

x1 ∨ x2 ∨ ¬x3 ∨ 0 ∨ x5 ∨ ¬x6 ∨ 0 ∨ x8 = *

Хоть известные величины равны 0, но под неизвестными переменными может скрываться 1, поэтому значение формулы может быть как 0, так и 1. Я обозначил его *.

F=1 из таблицы истинности подходит

Подставим третью строку таблицы истинности:

0 ∨ x2 ∨ ¬x3 ∨ 0 ∨ x5 ∨ ¬x6 ∨ x7 ∨ x8 = *

F=0 из таблицы истинности подходит

Следовательно, третья формула подходит под фрагмент таблицы истинности.

 

Четвертую формулу предлагаю проверить читателю самостоятельно.

 

Ответ: 3

Обратим внимание на то, что формула представляет собой три множителя. Это означает, что каждый из этих множителей должен быть равен 1, чтобы значение функции также было равно 1.

То есть:

x = 1. Значит, x – третий столбец

¬y = 1. Значит, y = 0, y – второй столбец.

???	y	x	???	F
0	0	1	0	1
0	0	1	1	1
1	0	1	1	1

 

Остается проверить два варианта:

z

y

x

w

F

И

w

y

x

z

F

 

Первый вариант подошел:

z	y	x	w	F
0	0	1	0	1
0	0	1	1	1
1	0	1	1	1

 

Ответ: zyxw

Пользуясь знаниями комбинаторики, определим количество возможных ответов. Оно равно числу перестановок из 3 элементов: P₃ = 3! = 1 * 2 * 3 = 6. Перечислим эти решения:

xyz

xzy

yxz

zxy

yzx

zyx

Во фрагменте таблицы истинности во всех строках значения выражения равны 0. Это возможно только в случае, когда 1 → 0 = 0. Следовательно:

x ∨ y = 1

z ≡ x = 0

Рассмотрим выражение z ≡ x = 0. Получается, что не должно быть совпадающих значений в колонках z и x. Но у нас есть два совпадающих нуля во второй и третьей колонке таблицы истинности. Следовательно, невозможны такие ответы:

yxz

yzx

 

У нас остаются следующие потенциальные ответы:

xyz

xzy

zxy

zyx

 

Чтобы x ∨ y = 1, нужно, чтобы x и y не были нулями одновременно. Следовательно, невозможны ответы:

zxy

zyx

 

Остаются следующие потенциальные ответы:

xyz

xzy

 

Предположим, что ответ xyz верен: 

Переменная 1	Переменная 2	Переменная 3	Функция
x	y	z	F
	0	0	0
	0		0

 

Тогда попробуем заполнить таблицу истинности. Чтобы x ∨ y = 1, нужно, чтобы первая колонка была 1:

Переменная 1	Переменная 2	Переменная 3	Функция
x	y	z	F
1	0	0	0
1	0		0

 

Чтобы z ≡ x = 0 нужно, чтобы z не совпадал с x:

Переменная 1	Переменная 2	Переменная 3	Функция
x	y	z	F
1	0	0	0
1	0	0	0

 

Но тогда две строчки в таблице истинности совпадают, что невозможно! Следовательно, xyz ответом быть не может.

 

Проверим xzy:

Переменная 1	Переменная 2	Переменная 3	Функция
x	z	y	F
1	0	0	0
1	0	1	0

 

Строчки не совпадают, следовательно, xzy является ответом.

Ответ: xzy

В таблице истинности все ответы – 1. Сама функция представляет собой логическое «и» (логическое умножение), поэтому каждый из множителей равен 1:

(x → y) =1

(y → z) = 1

Множители представляют собой каскад импликаций (следований). Импликация равна 0 только в одном случае:

1 → 0 = 0.

Недопустимо иметь ноль в ответе ни в одной из импликаций (такой «множитель» обнулит всё выражение). Наоборот, мы заинтересованы в том, чтобы множители имели вид:

0 → ? = 1

Такой множитель всегда равен 1 независимо от второй переменной. Следовательно, мы заинтересованы в том, чтобы в первом множителе первая переменная была всегда равна 0. То есть x=0:

(0 → y) ∧ (y → z) = 1.

Перем. 1	Перем. 2	Перем. 3	Функция
???	???	x	F
1	1	0	1
0	1	0	1

 

Поскольку 0 → ? = 1 при любом значении переменной, а у нас есть столбец со всеми значениями 1, то:

(0 → y) ∧ (y → 1) = 1.

Это столбец z:

Перем. 1	Перем. 2	Перем. 3	Функция
???	z	x	F
1	1	0	1
0	1	0	1

 

Для y остается первый столбец:

Перем. 1	Перем. 2	Перем. 3	Функция
y	z	x	F
1	1	0	1
0	1	0	1

 

Ответ: yzx

Перезапишите выражение в виде системы и совокупности.

Как и в предыдущей задаче, решать данную задачу перебором очень долго, так как количество потенциальных решений равно количеству перестановок от 4! = 1 * 2 * 3 * 4 = 24.

Воспользуемся свойством логического «или»: наличие хотя бы одной 1 приведет к 1 в значении выражения. Перезапишем выражение в виде системы: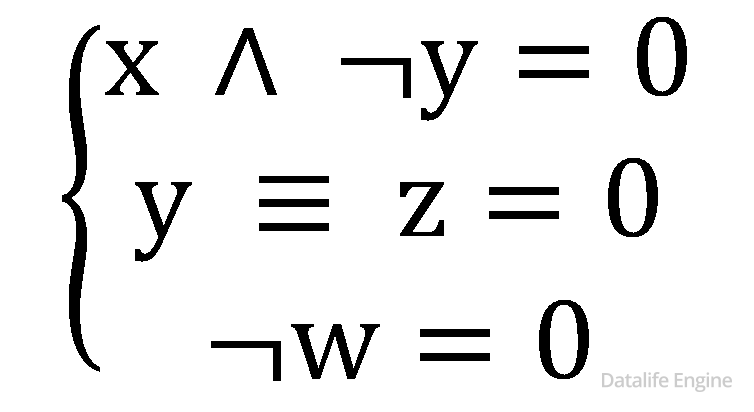 

Продолжим упрощение

 

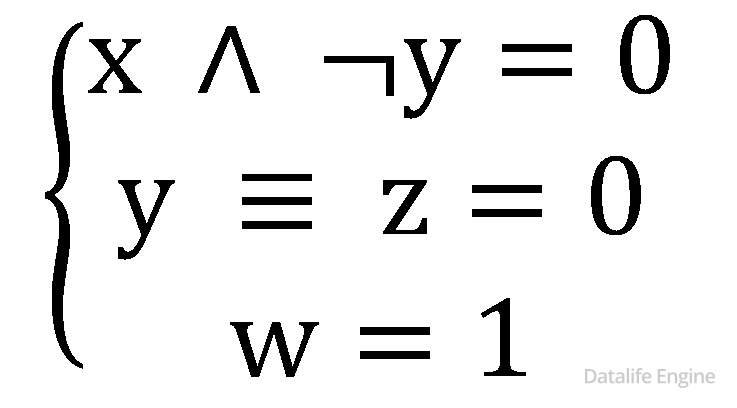
У нас есть столбик №1, заполненный единицами. Ему должно соответствовать отрицание во фрагменте выражения, то есть ¬w. Мы нашли первое соответствие: 

w	???	???	???
	0
1	0		0
1		0	0

 

По свойству тождества   тогда, когда значения переменных не совпадают:

 

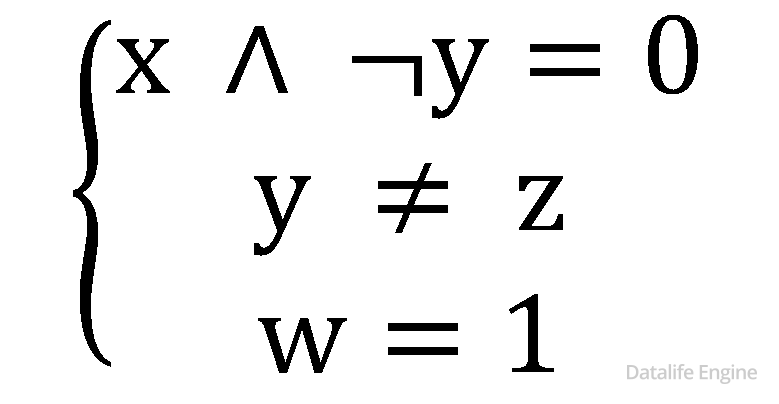
То есть невозможны следующие варианты:

w у ??? z   0     1 0   0 1   0 0

w z ??? y   0     1 0   0 1   0 0

w ??? y z   0     1 0   0 1   0 0

w ??? z y   0     1 0   0 1   0 0

 

Остаются два возможных варианта расположения y и z:

w у z ???   0     1 0   0 1   0 0

w z y ???   0     1 0   0 1   0 0

 

Но оба эти варианта подразумевают, что x – это четвертая колонка:

w	???	???	x
	0
1	0		0
1		0	0

 

Рассмотрим первое «слагаемое» x ∧ ⌐y = 0. Логическое «и» ложно тогда, когда хотя бы один из «множителей» равен 1:

 

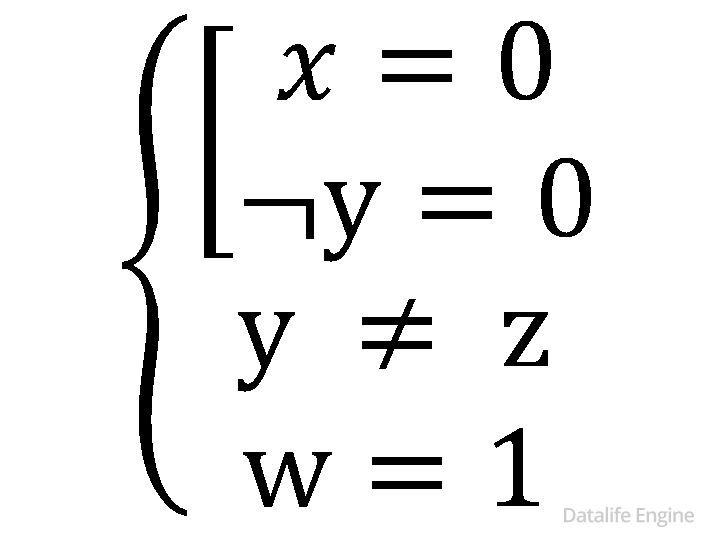
То есть:

 

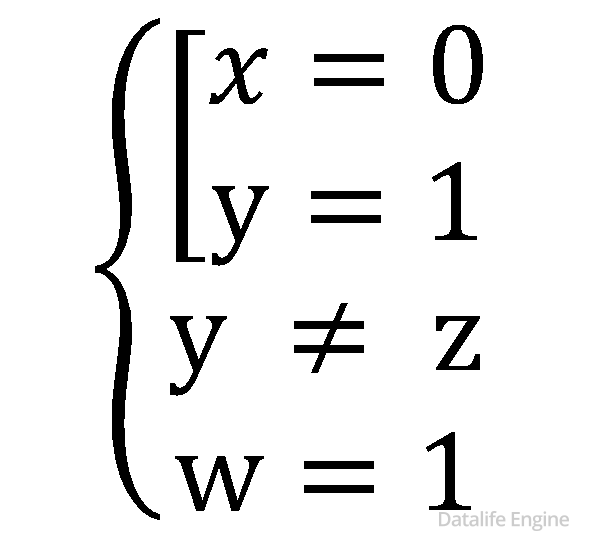
В случае, если y – вторая колонка, то

w	y	z	x	F
	0			?
1	0		0	0
1		0	0	0

 

Но то же самое получается и при другом расположении y и z:

w	z	y	x	F
	0			?
1	0		0	0
1		0	0	0

 

Какой из решений выбрать? Здесь нужно воспользоваться фразой «фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна». Здесь ключевое слово «все». Расположение y в третьей колонке уменьшает количество возможных вариантов.

Ответ: wzyx

Поскольку функция при всех приведенных строчках таблицы истинности равна 1 и представляет собой конъюнкцию двух частей, мы можем разделить выражение на две части, превратив его в систему:

(x → y) ≡ (y → z) = 1

y ∨ w = 1

Рассмотрим сперва второе выражение, как наиболее простое. Поскольку это дизъюнкция, то одновременно не может y=0 и w=0. Предположим, что y – первая колонка, тогда w не может быть ни 2, ни 3, ни 4 (получится два нуля в таблице истинности), следовательно, y не может быть в первой колонке. Аналогично w не может быть в первой колонке:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
Не y, не w ???	???	???	???	F
0		0		1
0	0		0	1
			0	1

 

Рассмотрим первое выражение. Оно представляет собой тождество импликаций (следований). Поскольку в таблице истинности одни нули, то

0 → ? = 1.

Поскольку в таблице истинности импликаций три строчки с ответом 1 и только одна – с ответом 0, весьма вероятно, что в нашем примере импликации равны 1, то есть

1 ≡ 1 = 1

(x → y) = 1

(y → z) = 1

Рассмотрим второе выражение (y → z) = 1. Мы заинтересованы, чтобы y как можно чаще был равен 0. Поскольку первая колонка не годится, пусть y будет четвертой колонкой:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
не w ???	???	???	y	F
0		0		1
0	0		0	1
			0	1

 

Вспомним, что, так как y ∨ w = 1, в таблице в одной строчке не может быть одновременно двух нулей y = 0 и w = 0, следовательно, w – это третья переменная:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
???	???	w	y	F
0		0		1
0	0		0	1
			0	1

 

Аналогично рассуждениям про y, из-за выражения (x → y) = 1 нужно, чтобы x = 0 в таблице истинности как можно чаще, следовательно, x – первая колонка:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
x	???	w	y	F
0		0		1
0	0		0	1
			0	1

 

Для z остается только вторая колонка:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
x	z	w	y	F
0		0		1
0	0		0	1
			0	1

 

Решая задачу, мы сделали ряд предположений, поэтому наш результат вероятен, но не обязательно правилен. Сделаем проверку, подставив значения из таблицы истинности в исходное уравнение: 

((x → y) ≡ (y → z)) ∧ (y ∨ w).

Первая строка:

((0 → y) ≡ (y → z)) ∧ (y ∨ 0)

(1 ≡ (y → z)) ∧ y

Чтобы выражение было истинным, нужно, чтобы y = 1:

(1 ≡ (1 → z)) ∧ 1

(1 ≡ (1 → z))

И z = 1 тоже:

1 ≡ (1 → 1)

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
x	z	w	y	F
0	1	0	1	1
0	0		0	1
			0	1

 

Вторая строка:

((0 → 0) ≡ (0 → 0)) ∧ (0 ∨ w)

(1≡1) ∧ w

1 ∧ w

w

Следовательно, w = 1:

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
x	z	w	y	F
0	1	0	1	1
0	0	1	0	1
			0	1

 

Третья строка:

((x → 0) ≡ (0 → z)) ∧ (0 ∨ w)

((x → 0) ≡ 1) ∧ w

Чтобы это выражение было истинным, нужно:

z – любое

w = 1

x → 0 = 1

x = 1

Переменная 1	Переменная 2	Переменная 3	Переменная 4	Функция
x	z	w	y	F
0	1	0	1	1
0	0	1	0	1
1	?	1	0	1

 

Итак, наше расположение переменных вполне соответствует таблице истинности при приведенном заполнении её единицами.

Ответ: xzwy

Используя знания комбинаторики, определите, сколько строчек в таблице истинности. Затем воспользуйтесь свойством конъюнкции, когда единственный ноль обнуляет всё выражение.

Воспользуемся знаниями комбинаторики. Поскольку у нас пять переменных, которые могут принимать значения 0 и 1, то в таблице истинности строчек:

2⁵ = 32

Из них только для одной значение выражения равно 1 (когда все переменные равны 1), так как логическое «и» при наличии хотя бы одного 0 имеет 0 в качестве результата. Следовательно, количество наборов значений переменных, при которых выражение ложно, равно 32 – 1 = 31.

Ответ: 31.

Пользуясь знаниями комбинаторики, определите, сколько строчек в таблице истинности. Составьте заготовку для таблицы истинности объединенного выражения F ∨ G. Так как есть несовпадающие строчки, определите, чему равно итоговое выражение в этих строчках.

Составим заготовку таблицы истинности для итогового выражения и заполним её в соответствии с данными задачи:

X1	X2	X3	X4	X5	F	G
					1	1
					1	1
					1	1
					1	1

 

Так как есть пятая строчка в таблицах истинности с одинаковыми значениями, то очевидно, что итог выражений равен 0:

X1	X2	X3	X4	X5	F	G
					0	0
					1	1
					1	1
					1	1
					1	1

 

Посчитаем объединенное выражение:

X1	X2	X3	X4	X5	F	G	F ∨ G
					0	0	0
					1	1	1
					1	1	1
					1	1	1
					1	1	1

Так как имеется пять переменных, каждая из которых принимает значения 0 или 1, то, пользуясь знаниями комбинаторики, определим количество строчек в таблице истинности как 2⁵ = 32. Следовательно, неравных строк 32 – 5 = 27

	X1	X2	X3	X4	X5	F	G	F ∨ G
5 Равных строчек						0	0	0
						1	1	1
						1	1	1
						1	1	1
						1	1	1
27     неравных строчек
	…

 

Так как в неравных строчках X1, X2, … , X5 для таблиц истинности F и G совпадают, то строки могут различаться только значениями F и G:

	X1	X2	X3	X4	X5	F	G	F ∨ G
5 Равных строчек						0	0	0
						1	1	1
						1	1	1
						1	1	1
						1	1	1
27  неравных строчек						0	1
						0	1
						1	0
						1	0
	…
						0	1

 

По свойствам конъюнкции значения в объединенном выражении для этих строк будут равны 1:

	X1	X2	X3	X4	X5	F	G	F ∨ G
5 Равных строчек						0	0	0
						1	1	1
						1	1	1
						1	1	1
						1	1	1
27     неравных строчек строчки						0	1	1
						0	1	1
						1	0	1
						1	0	1
	…
						0	1	1

 

Следовательно, всего строк с 1 равно 27 + 4 = 31.

Ответ: 31