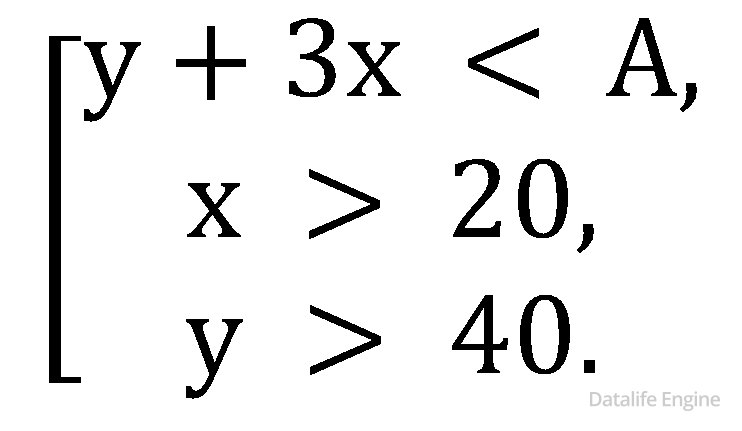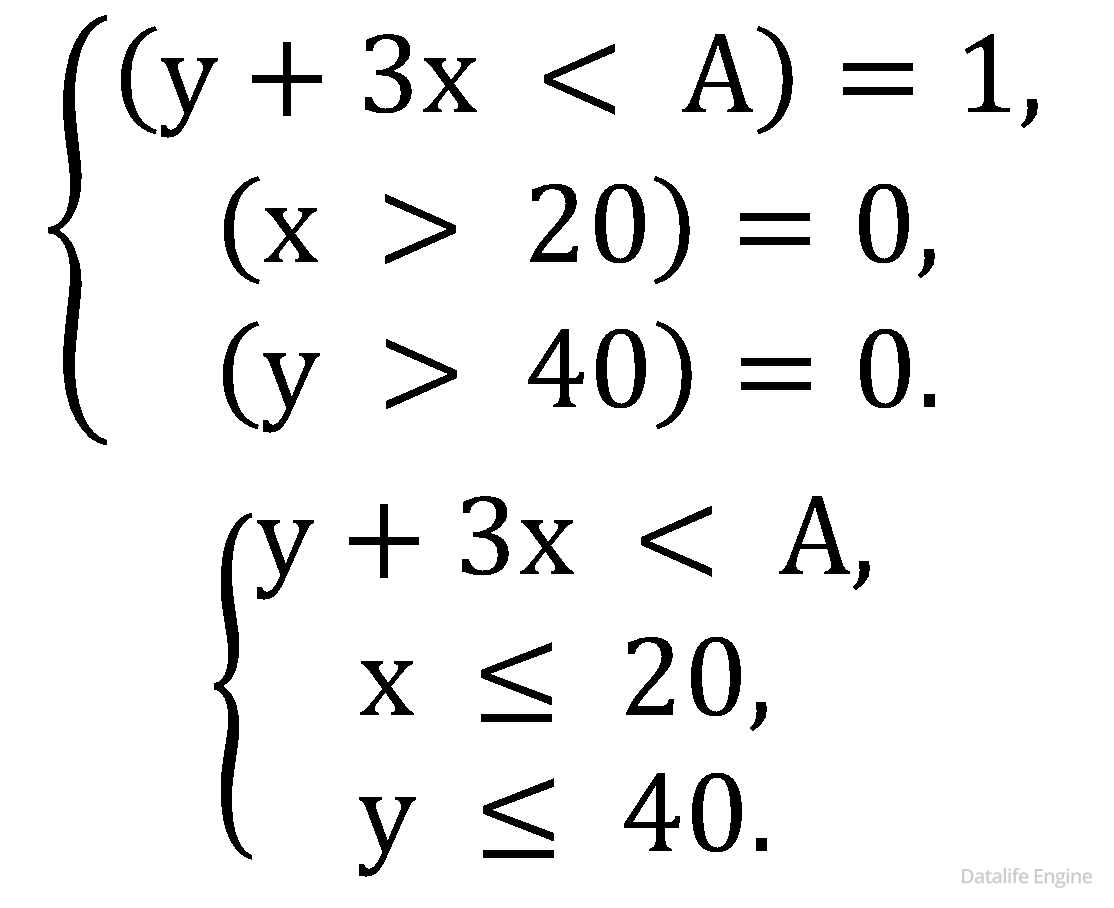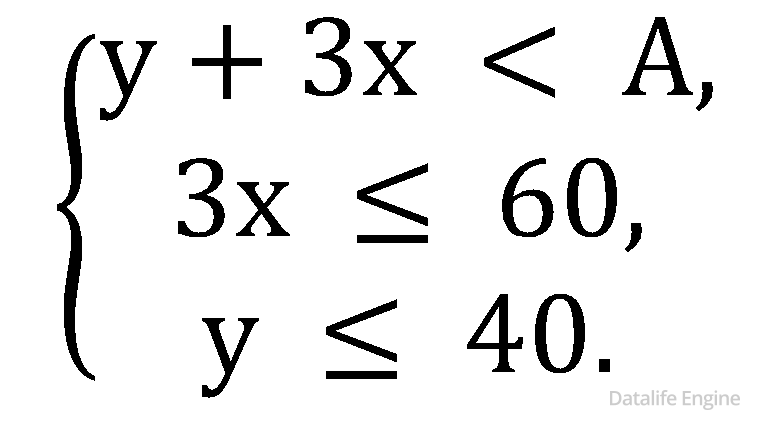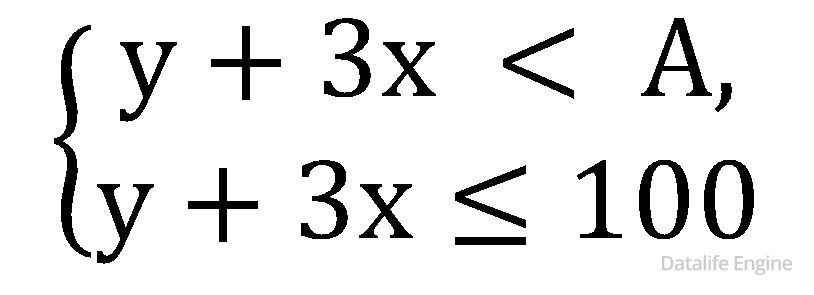Задача 4.2.0. Укажите наименьшее значение А, при котором выражение
(y + 3x < A) ∨ (x > 20) ∨ (y > 40)
истинно для любых целых положительных значений x и y.
На основе выражения составьте систему неравенств с параметром и решите её.
Эта задача – типичная задача с параметром из ЕГЭ по математике, которой придан «информатический» вид. Задачи с параметром можно решать графически и аналитически. Приведем оба решения.
Поскольку в нашем выражении – дизъюнкция (логическое «или»), то наше выражение – не система, а совокупность:
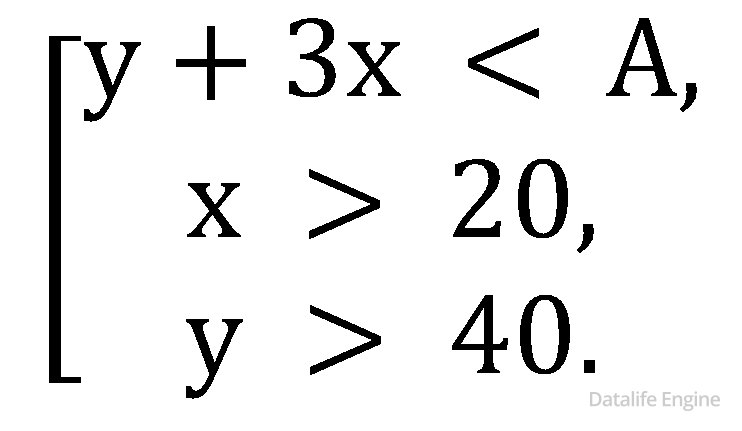
Проанализируем, при каких значениях x и y истинность выражения не зависит от А (по свойству логического «или» наличие истины в одном из «слагаемых» делает всё выражение истинным):
|
(y+3x < A)
|
∨ (x > 20)
|
∨ (y > 40)
|
Значение выражения
|
|
?
|
0
|
1
|
1
|
|
?
|
1
|
0
|
1
|
|
?
|
1
|
1
|
1
|
Рассмотрим случай, когда первое «слагаемое» обязательно должно быть истинным:
|
(y+3x < A)
|
∨ (x > 20)
|
∨ (y > 40)
|
Значение выражения
|
|
1
|
0
|
0
|
1
|
Но на основе этого уже можно составить систему:
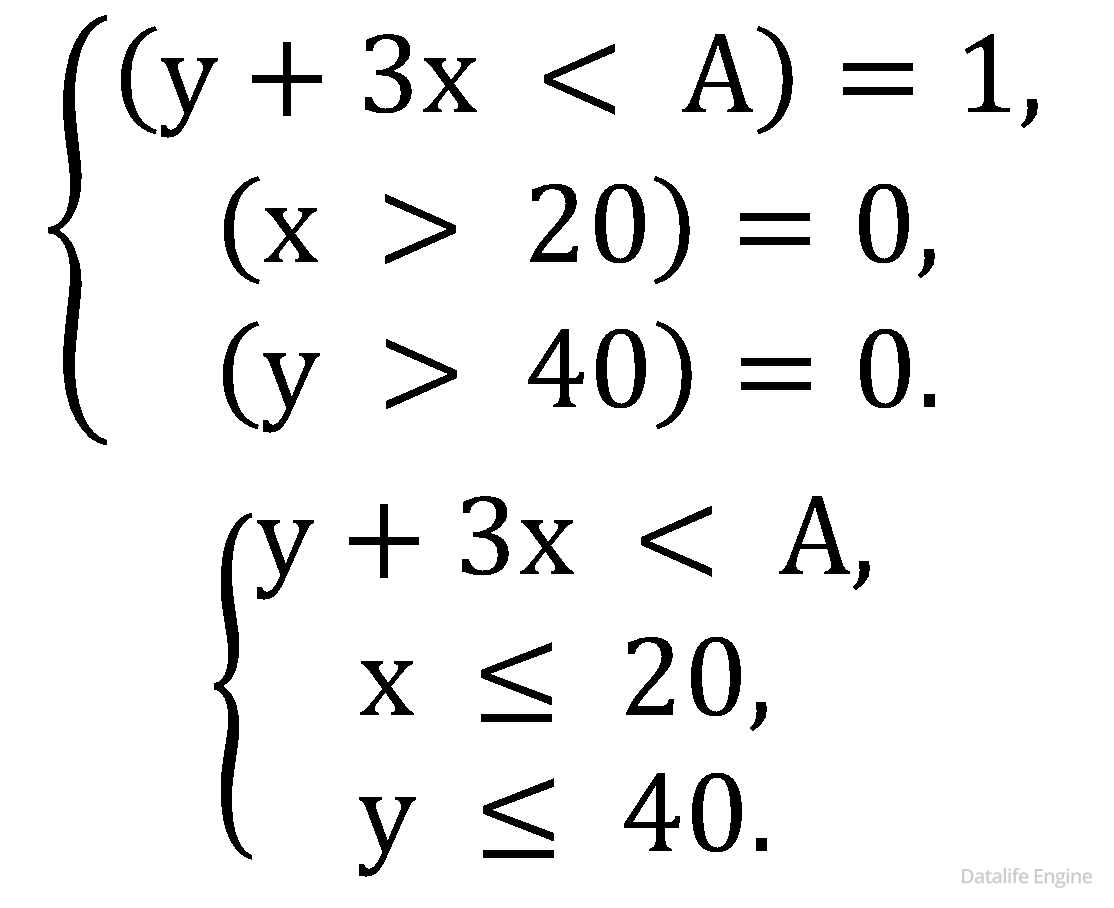
Решим систему:
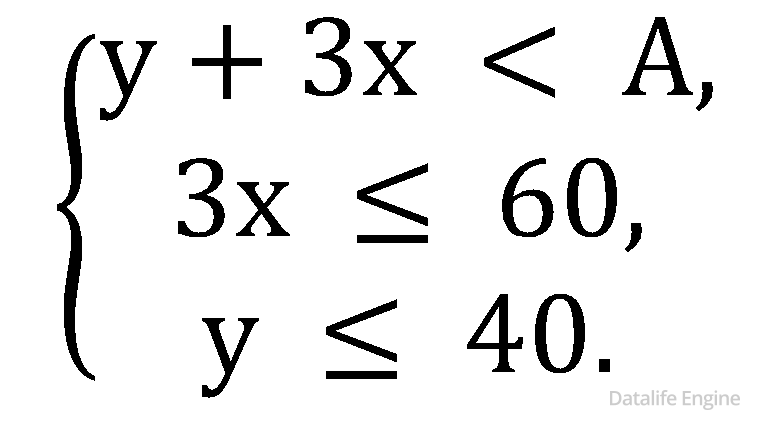
Сложим второе и третье неравенство:
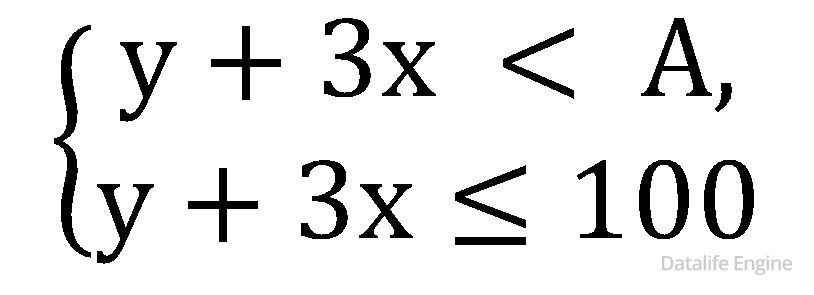
Поскольку система должна выполняться для любых x и y, то
100 < A
Минимальное целое А = 101.
Еще один способ решения – графический.
Закрасим области координатной плоскости, в которых выражение
(y + 3x < A) ∨ (x > 20) ∨ (y > 40) всегда истинно:
|
x > 20 соответствует область:
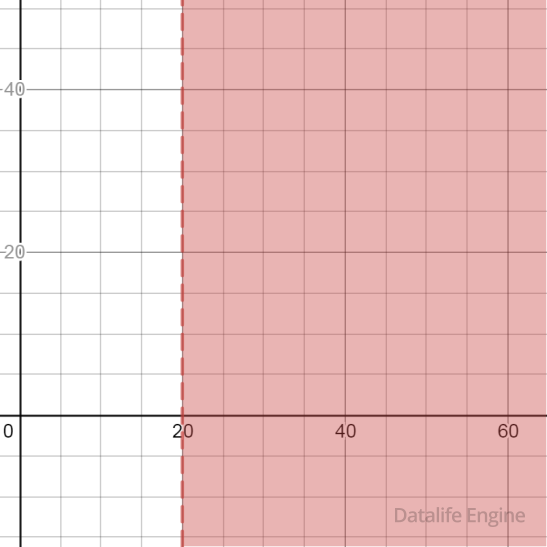
|
y > 40 соответствует область:
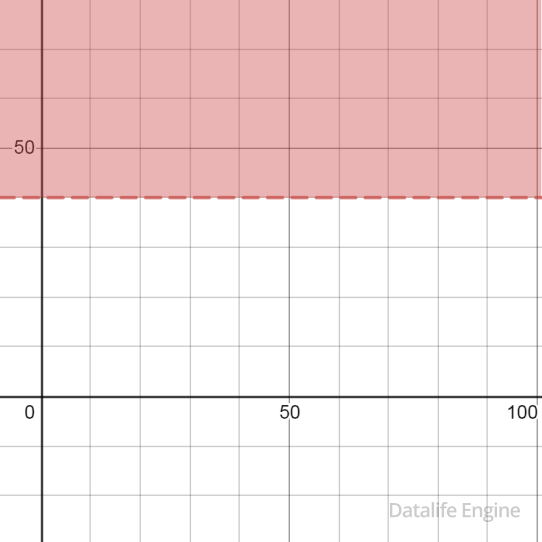
|
Совместим оба решения вместе:
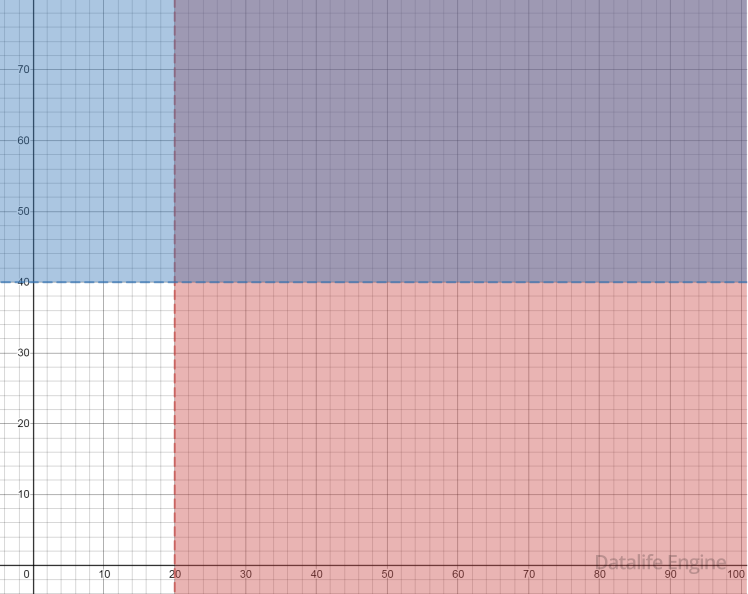
Очевидно, чтобы выражение было всегда истинным, надо, чтобы первое условие
(y + 3x < A) закрасило оставшуюся белую область. Рассмотрим кривую, соответствующую границе y + 3x = A. Ей соответствует наклоненная вниз прямая y = –3x + А, которая пересекает ось y в точке с координатами (0, А). То есть с помощью параметра А мы двигаем прямую вверх-вниз. Поскольку у нас неравенство со знаком <, то ему соответствует область ниже прямой:
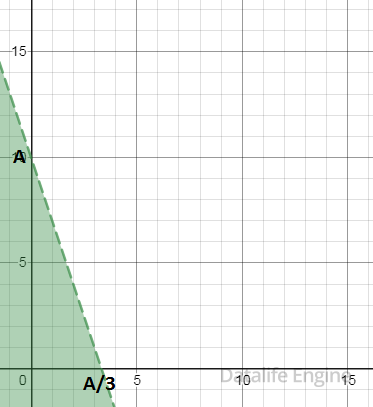
Совместим все координатные плоскости вместе:
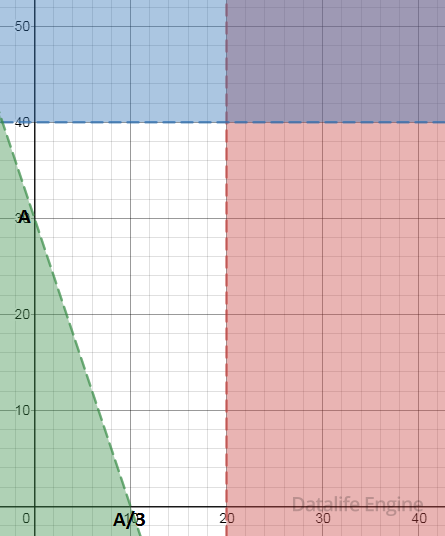
Чтобы у нас не было незакрашенных областей, нужно, чтобы наклонная прямая проходила через точку (20, 40):
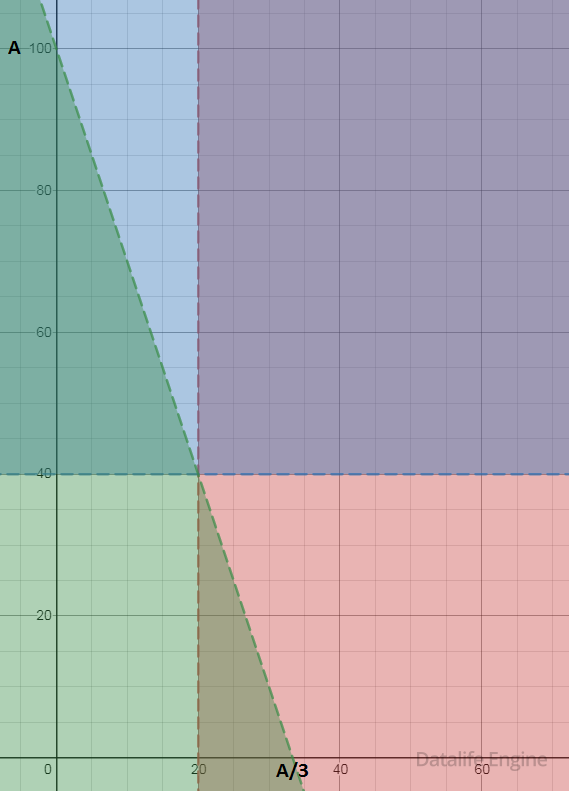
Ошибка. Подмывает найти А с помощью подбора по графику и написать ответ 100. Не будем торопиться и продолжим решать задачу аналитически:
Найдем значение А путем подстановки (20, 40) в неравенство y + 3x < A:
40 + 3 * 20 < A
100 < A
Поскольку мы ищем минимальное целое А, то А = 101.
В случае ошибочного ответа 100 выражение будет истинно во всех точках, кроме точки (20, 40).
Ответ: 101.
Опыт показывает, что графический метод решения задач с параметром проще аналитического. Решим еще несколько подобных задач посложнее.
Задача 4.2.0B. Для какого наименьшего целого неотрицательного числа A выражение
(3x + 4y > 66) ∨ (x ≤ A) ∨ (y < A)
тождественно истинно при любых целых неотрицательных x и y?
Решайте графически аналогично предыдущей. В каком-то смысле эта задача является обратной предыдущей.
Выражение истинно, если истинно первое «слагаемое» выражения, то есть
3x + 4y > 66.
Ему соответствует следующая закрашенная область координатной плоскости:
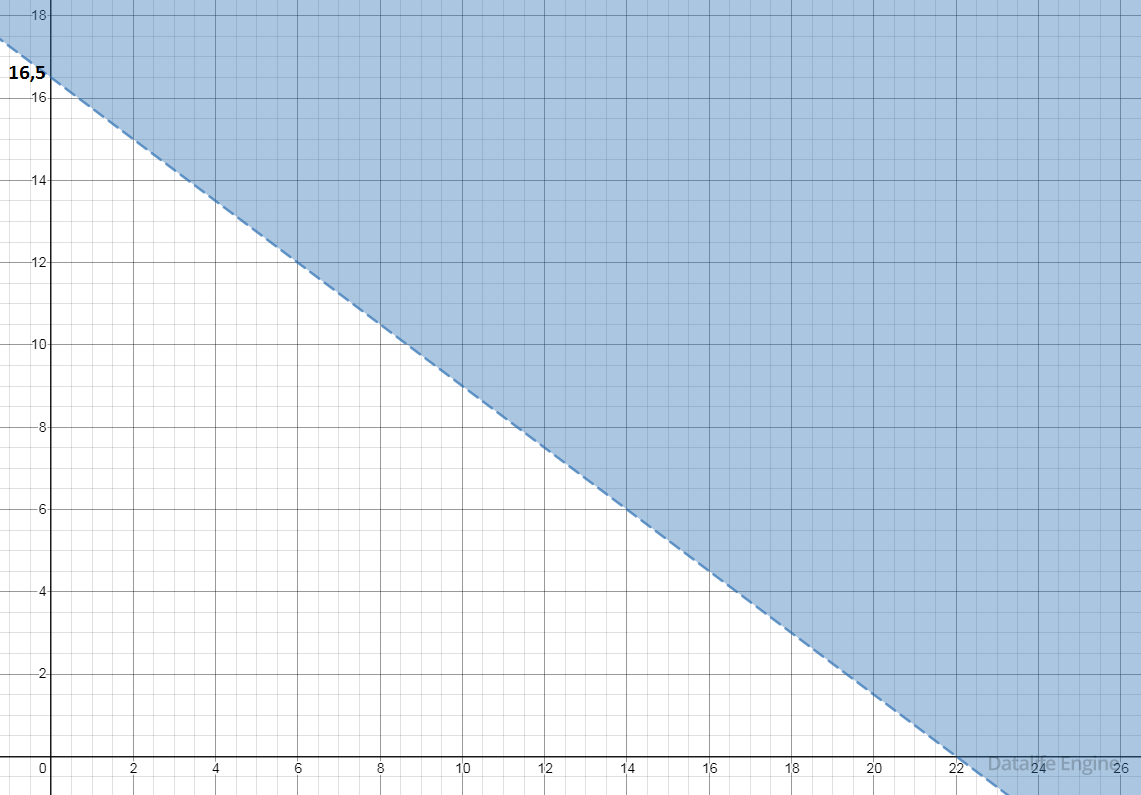
|
Второму слагаемому
соответствует область:
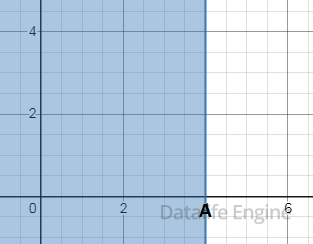
|
Третьему слагаемому
соответствует область:
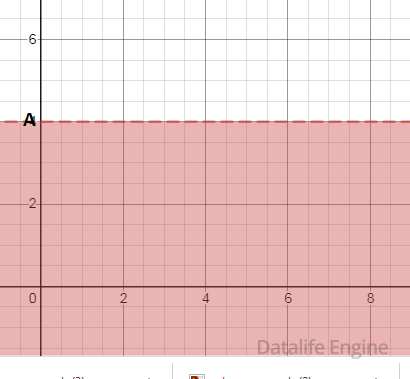
|
Совместим области на одной координатной плоскости:
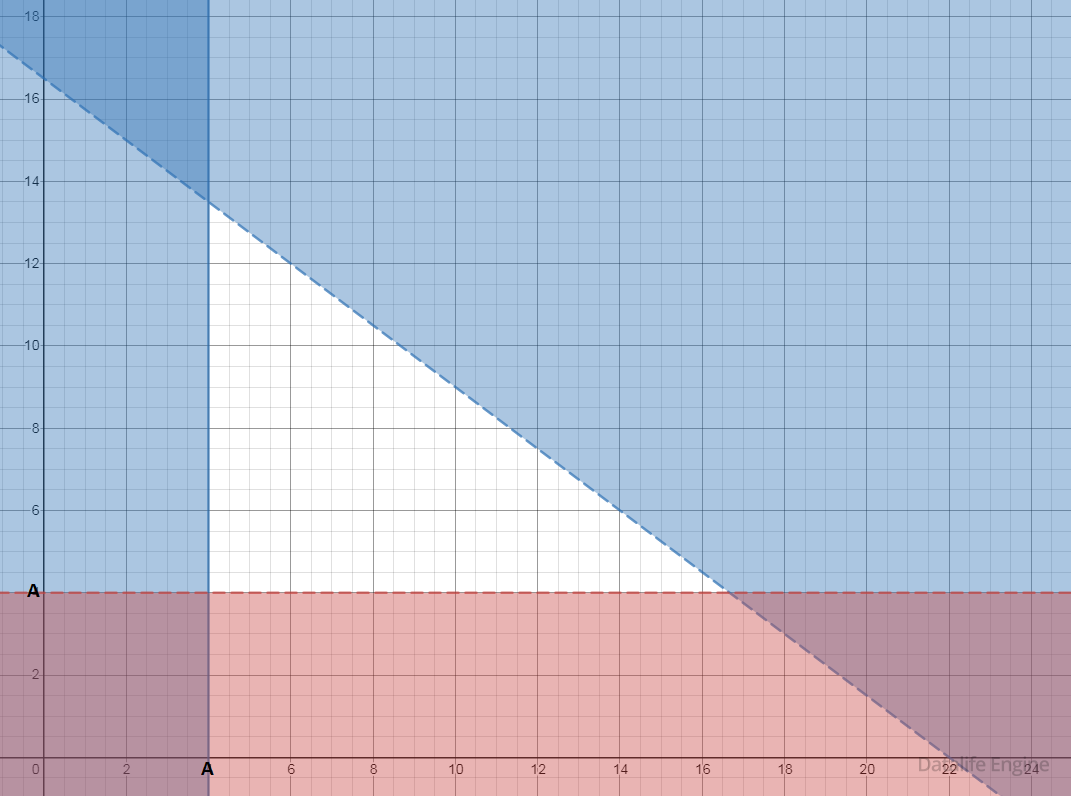
Поскольку «слагаемые» в выражении соединены с помощью логического «или», нам нужно, чтобы выполнялось хотя бы одно неравенство. Следовательно, мы должны выбрать такое А, чтобы на координатной плоскости не было незакрашенных областей:
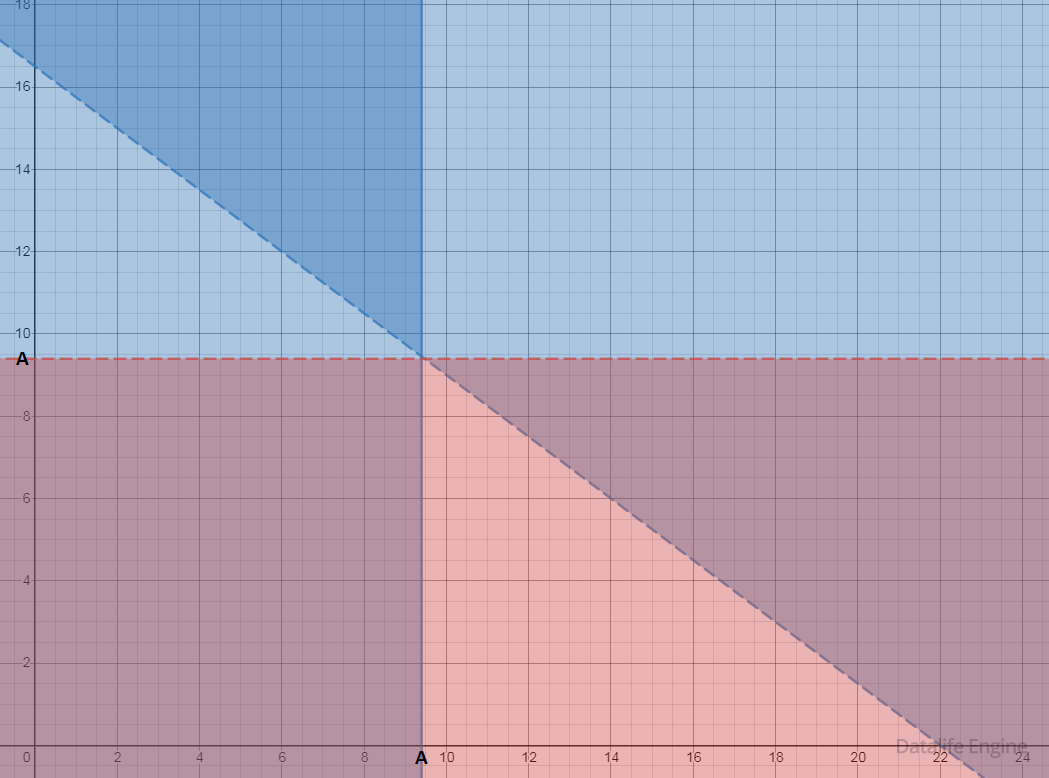
То есть точка с координатами (А, А) должна находиться на наклонной прямой. Найдем такое А, подставив его в 3x + 4y > 66.
3А + 4А > 66
7A > 66
A > 66/7 = 9 3/7
Поскольку мы ищем целое минимальное А, то А = 10.
Ответ: 10
Задача 4.2.0С. На числовой прямой задан отрезок A. Известно, что формула
((x ∈ A) → (x2 ≤ 81)) ∧ ((y2 ≤ 36) → (y ∈ A))
тождественно истинна при любых вещественных x и y. Какую наибольшую длину может иметь отрезок A?
Замените следование на дизъюнкцию и решайте графически, как предыдущую задачу.
Заменим следование на дизъюнкцию:
(⌐(x ∈ A) V (x2 ≤ 81)) ∧ ((y2 > 36) V (y ∈ A))
Рассмотрим первый «множитель» выражения:
⌐(x ∈ A) V (x2 ≤ 81)
Оно всегда истинно при –9 ≤ х ≤ 9:
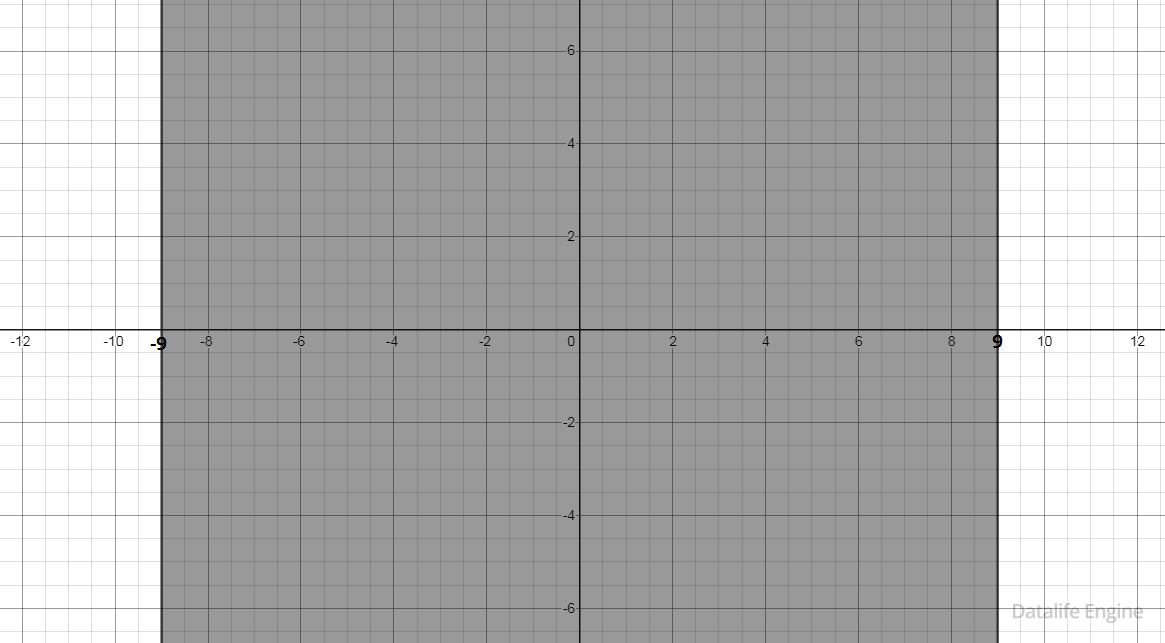
Чтобы оно было истинным на всей плоскости, нужно, чтобы в незакрашенных левой и правой областях было истинным выражение ⌐(x ∈ A). То есть точек А нет слева и справа. Значит, точки А могут быть только сосредоточенными внутри закрашенной области:
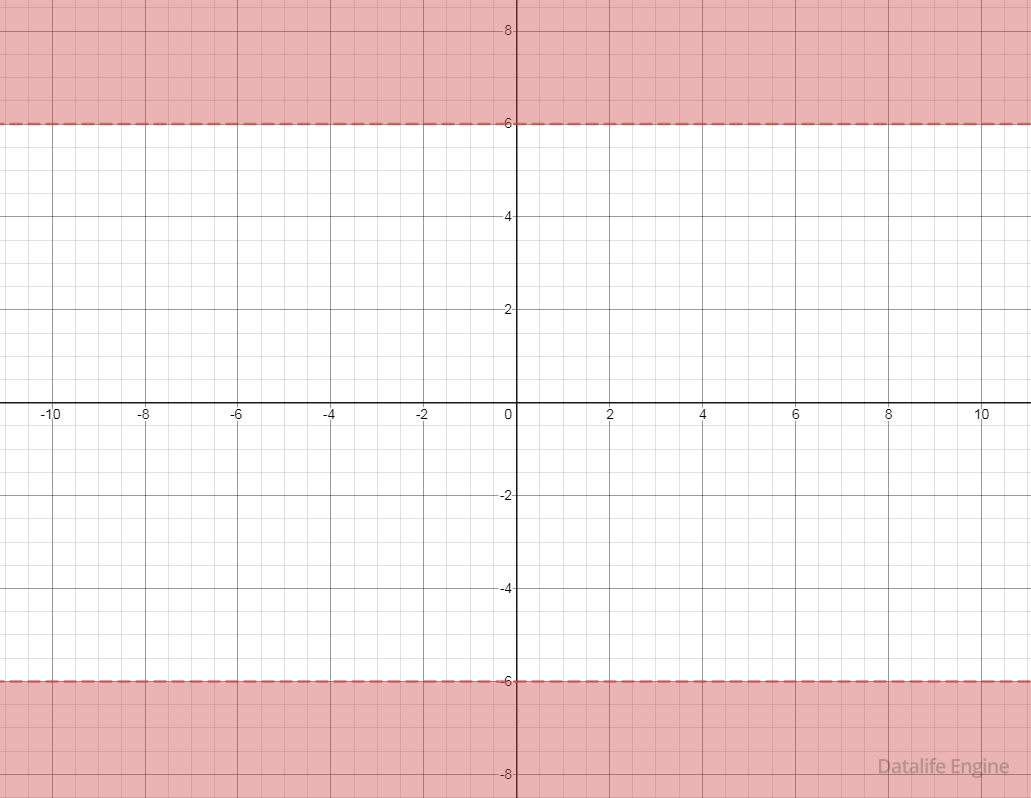
Рассмотрим второй множитель (y2 > 36) V (y ∈ A).
Он истинен в закрашенных областях:

Чтобы выражение было истинно на всей плоскости, нужно, чтобы точки незакрашенной области обязательно принадлежали А, то есть y ∈ A истинно. Значит:
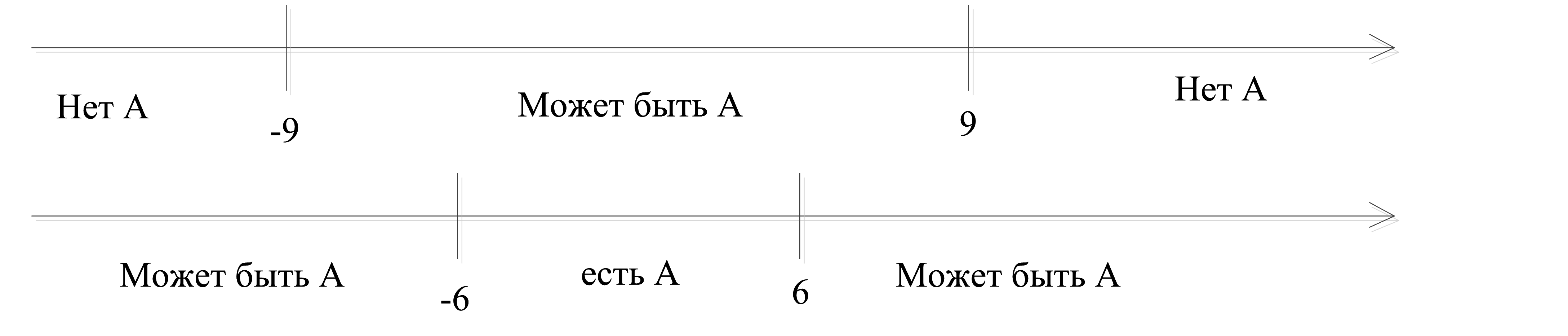
Теперь нам нужно совместить оба решения:

Так как у нас связка между логическими выражениями – «и», то оба условия должны выполняться одновременно. То есть нам нужно выбрать более жесткое решение. В частности:
Нет ∧ Может быть = Нет
Есть ∧ Может быть = Есть
После совмещения мы получаем:

То есть левая граница отрезка А «гуляет» между –9 и –6, а правая – между 6 и 9:
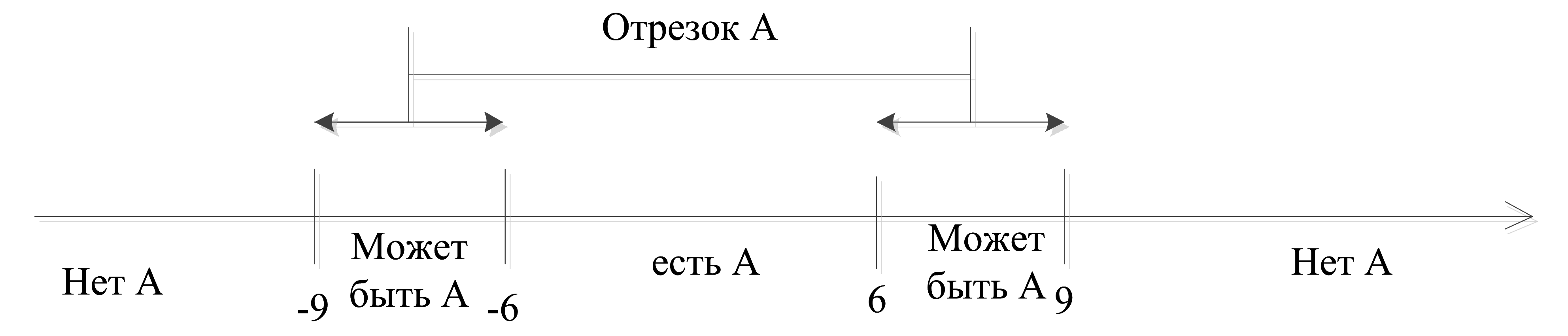
Значит, наибольшего размера достигает А тогда, когда он от -9 до 9. Его длина равна 18.
Ответ: 18
Задача 4.2.1. На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула
( (x ∈ А) → (x ∈ P) ) ∨ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
1) [0, 3]
2) [3, 11]
3) [11, 15]
4) [15, 17]
Замените следование на дизъюнкцию. На числовой области отметьте участки, которые не зависят от А. Затем для каждого участка напишите требование для расположения А – должен он там быть или нет. Затем выбирайте подходящий ответ.
Ошибка. Можно поступить формально: отметить на оси P, Q, отрезок из первого ответа. Затем проверять каждый получившийся на оси отрезок на соответствие уравнению. Но это слишком долго.
Заменим выражение:
( (x∈А) → (x∈P) ) ∨ (x∈Q) =
(x∈А) ∨ (x ∈ P) ∨ (x∈Q)
Отметим на оси отрезки P и Q:
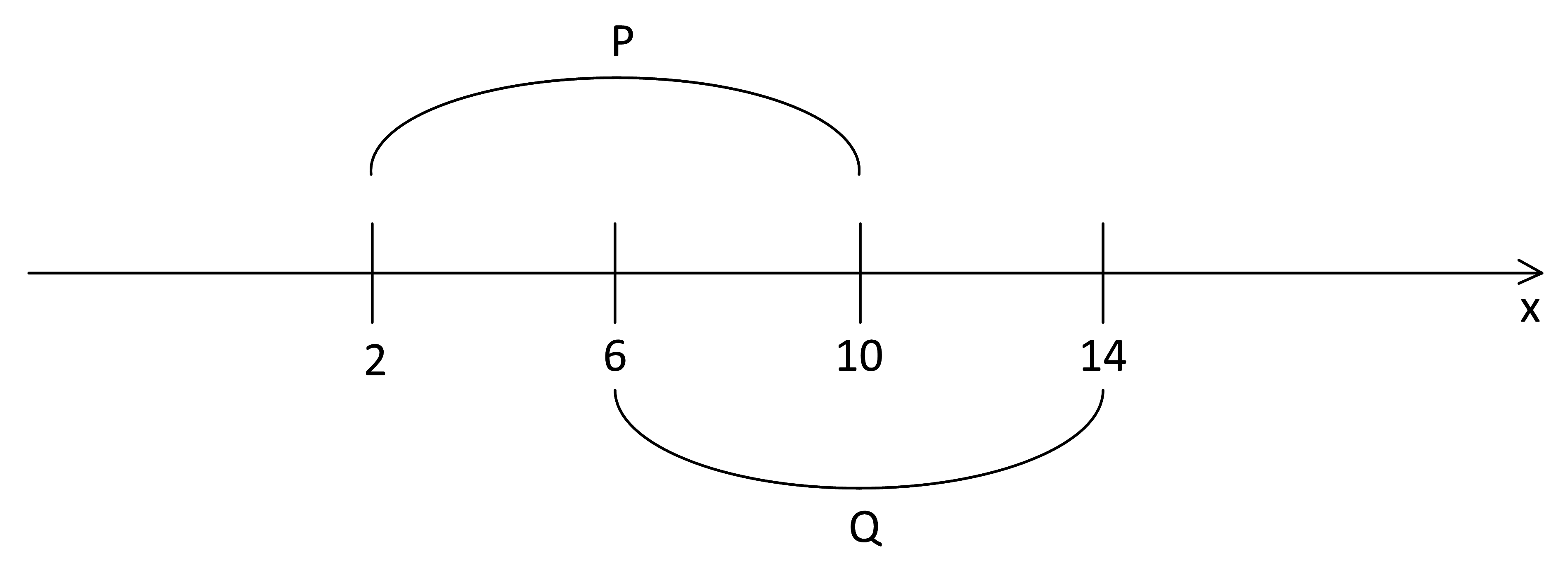
Наше выражение представляет собой логическое «или». Оно истинно, если хотя бы 1 из «слагаемых» истинен. Поэтому на участках P и Q выражение истинно вне зависимости от того, находится там отрезок А или нет. Заштрихуем истинную область на числовой оси:
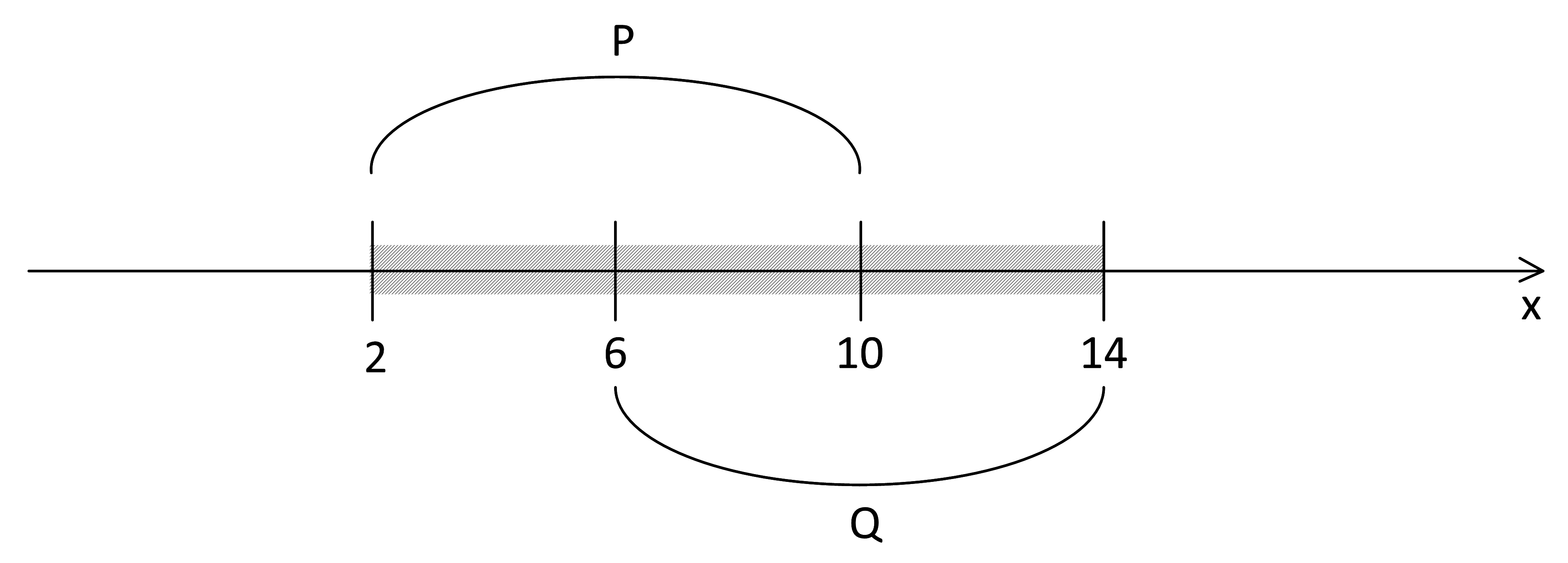
Сделаем выводы относительно А. В заштрихованной области от А ничего не зависит, вне заштрихованной области выражение с А должно быть истинным:
⌐(x ∈ А) = 1
x ∈ А = 0
Следовательно, А там нет.
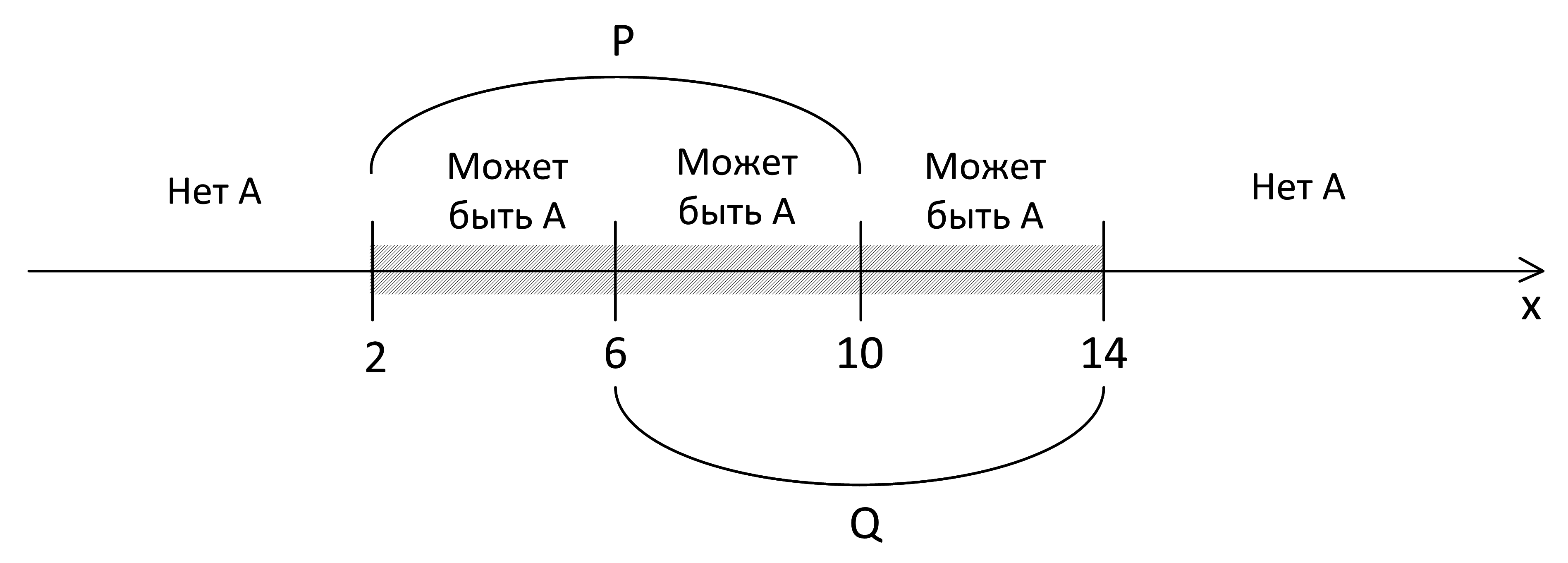
Подходящий под условия для А отрезок - [3, 11]:
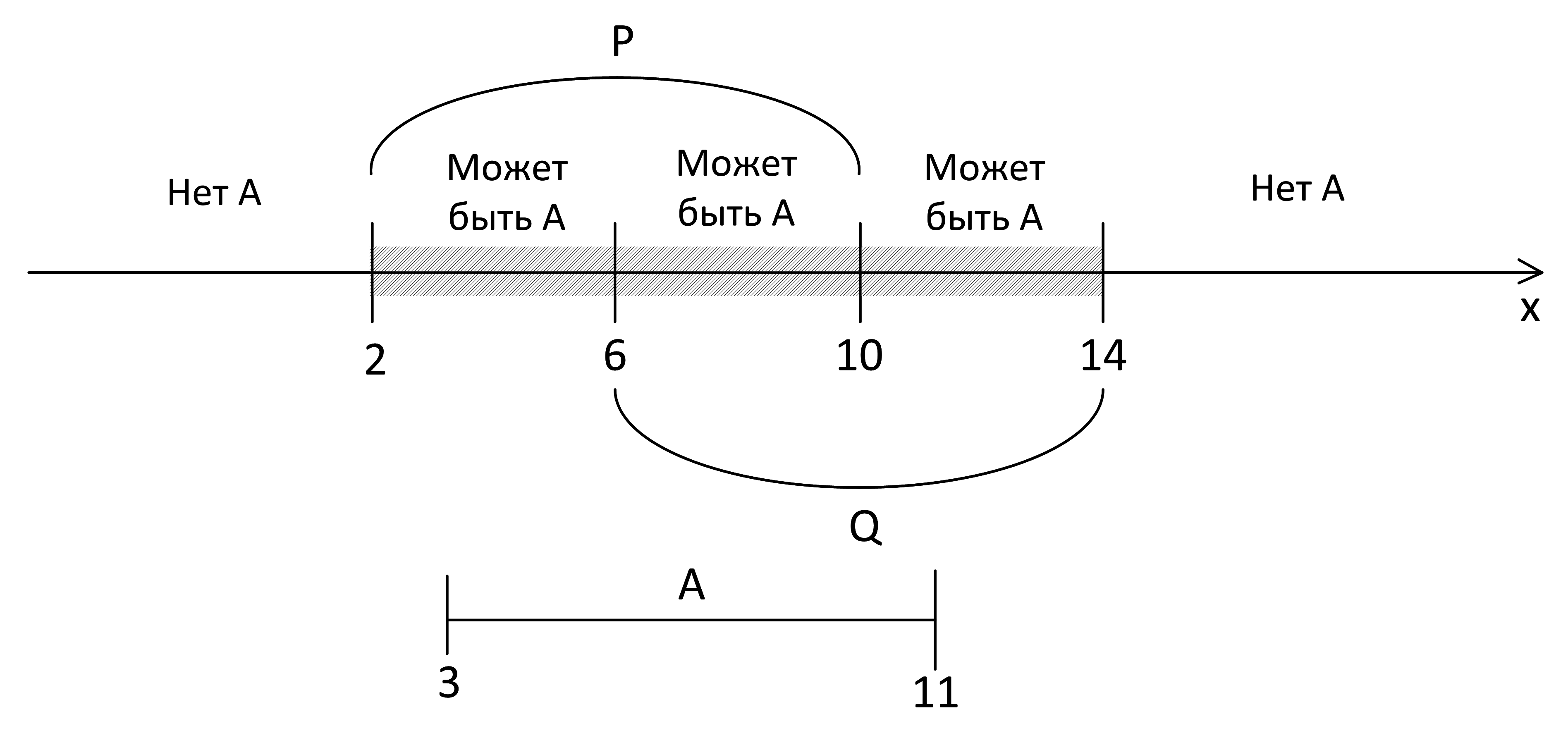
Ответ: 2
Задача 4.2.2. На числовой прямой даны два отрезка: P = [37, 60] и Q = [40, 77]. Укажите наименьшую длину такого отрезка A, что формула
(x∈P) → (((x∈Q) ∧ ⌐(x∈А))→⌐(x∈P))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Решайте, как в предыдущей задаче.
Упростим выражение, заменив следование на логическое «или»:
⌐(x∈P) ∨ (⌐((x∈Q) ∧ ⌐(x∈А)) ∨ ⌐(x∈P))
По закону де Моргана раскроем скобку в середине выражения:
⌐(x∈P) ∨ ((⌐(x∈Q) ∨ (x∈А)) ∨ ⌐(x∈P))
«Слагаемое» ⌐(x∈P) встречается два раза, оставим его только 1 раз и уберем лишние скобки:
⌐(x∈P) ∨ ⌐(x∈Q) ∨ (x∈А)
Отметим отрезки на числовой оси:
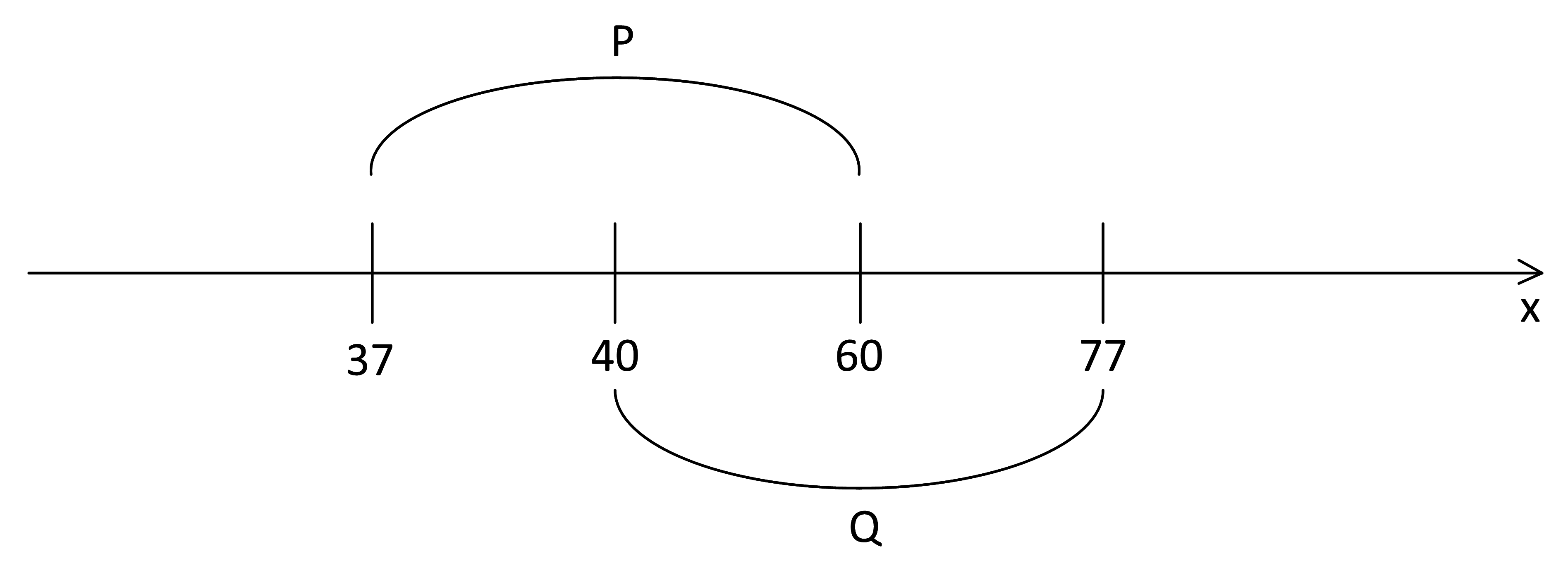
Логическое «или» истинно, когда истинно хотя бы одно из его слагаемых.
Заштрихуем область, в которой истинно ⌐(x∈P) (точки вне отрезка P):

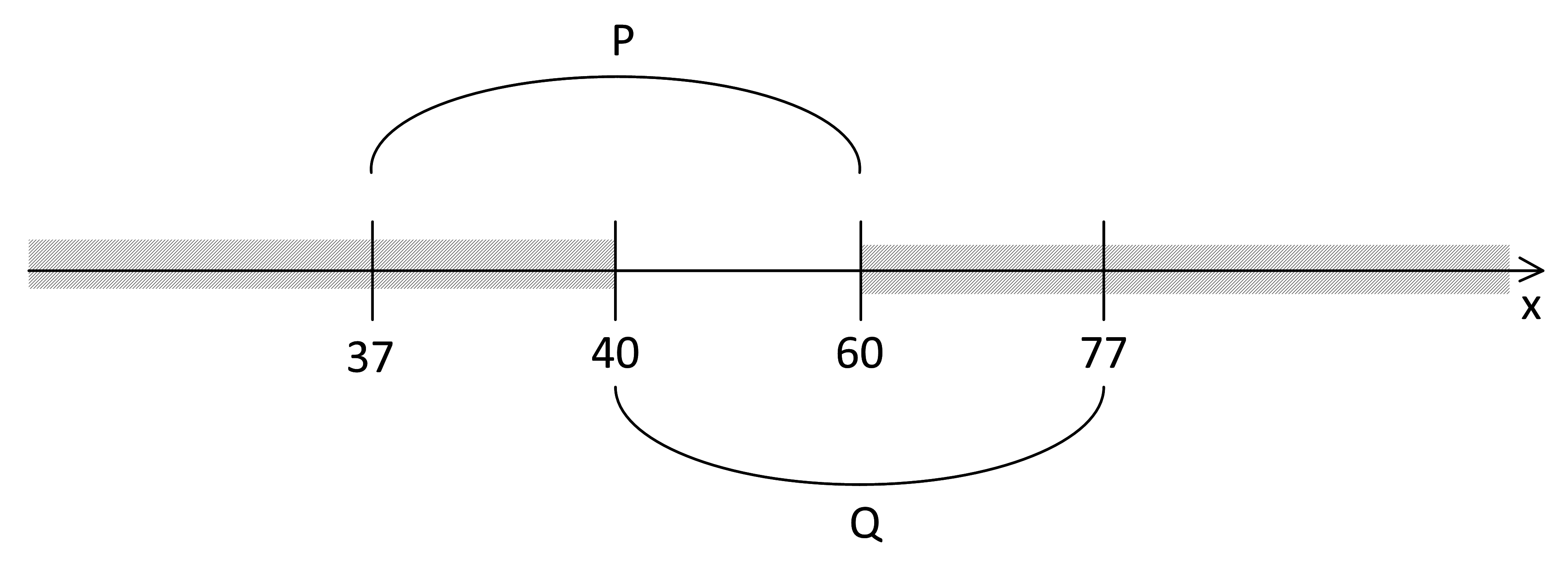
Сделаем выводы относительно А. В заштрихованной области от А ничего не зависит, вне заштрихованной области выражение с А должно быть истинным:
x∈А = 1
То есть вне заштрихованной области должно быть А:
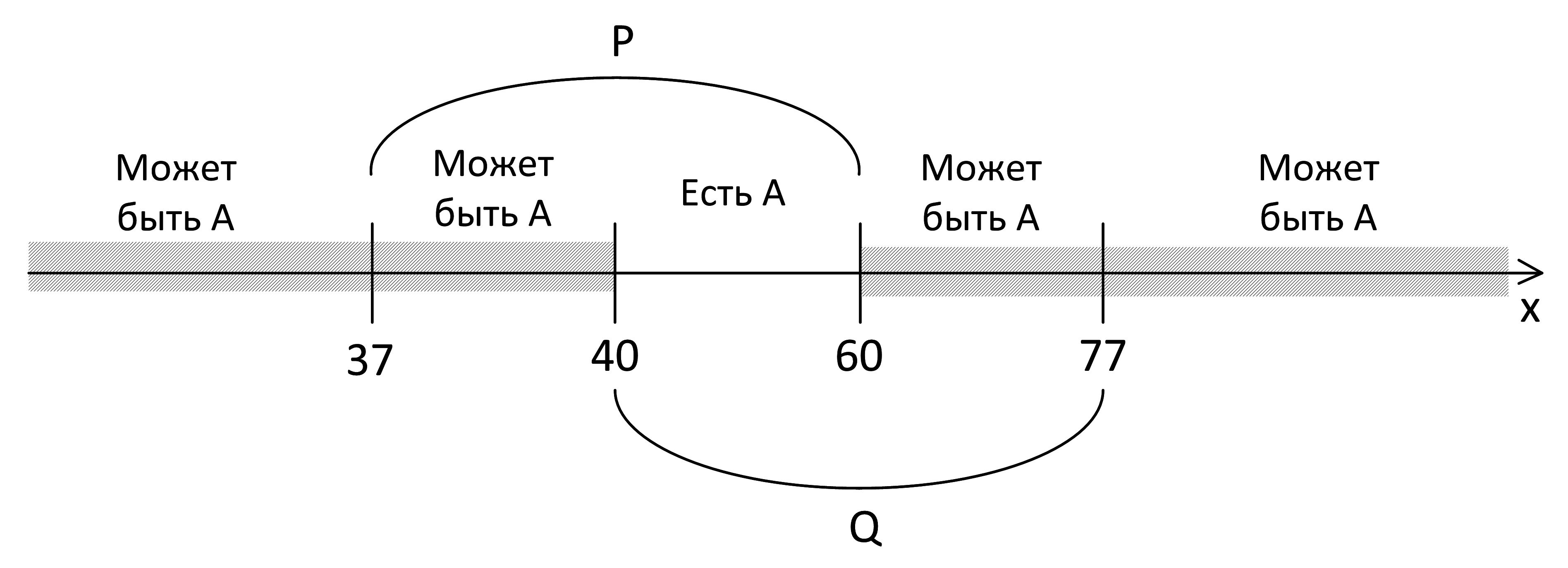
То есть А обязательно должно включать отрезок от 40 до 60, следовательно, минимальная длина А равна 60 – 40 = 20.
Ответ: 20
Задача 4.2.3. На числовой прямой даны два отрезка: P = [10, 35] и Q = [17, 48].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x∈A) → ¬(x∈P)) → ((x∈A) → (x∈Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Решайте, как в предыдущей задаче.
Упростим выражение, заменив следование на логическое «или»:
¬(¬(x∈A) ∨ ¬(x∈P)) ∨ (¬(x∈A) ∨ (x∈Q))
Правую скобку раскроем по закону де Моргана:
((x∈A) ∧ (x∈P)) ∨ ¬(x∈A) ∨ (x∈Q)
Отметим отрезки на числовой оси:
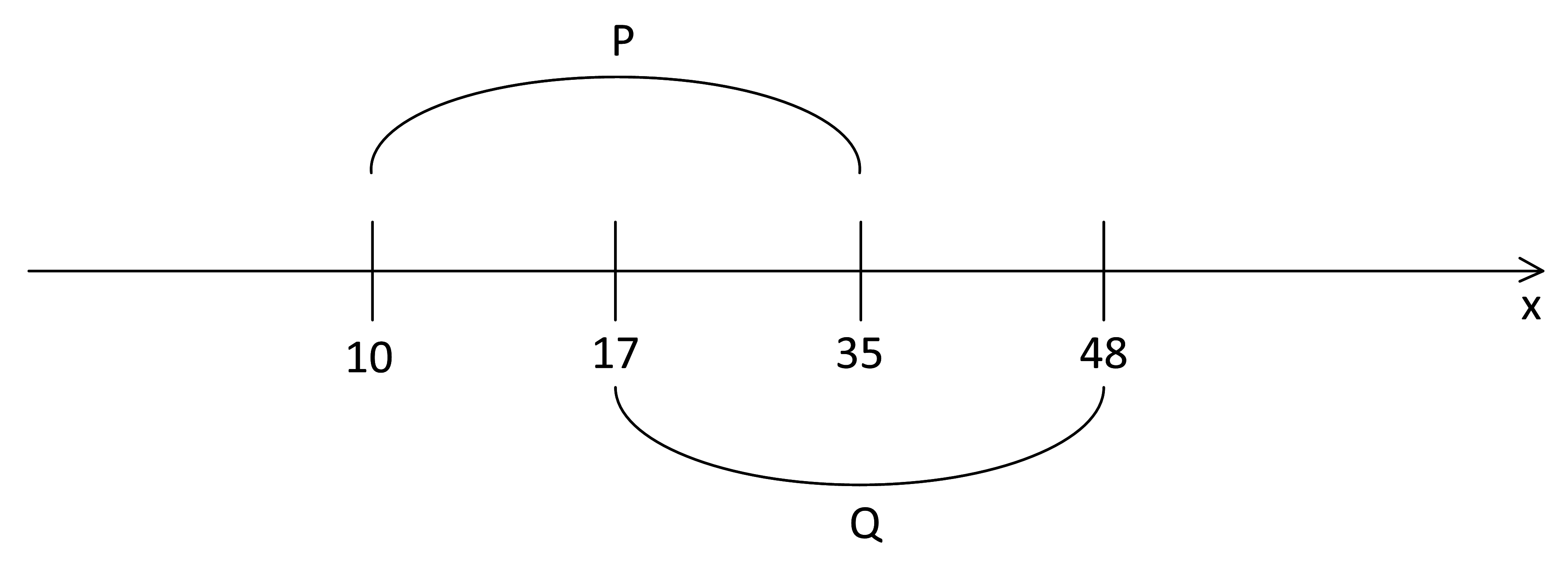
Логическое «или» истинно, когда истинно хотя бы одно из его слагаемых. В нашем случае в выражении три слагаемых и первое имеет сложную структуру.
Заштрихуем область, в которой истинно x∈Q (точки отрезка Q):
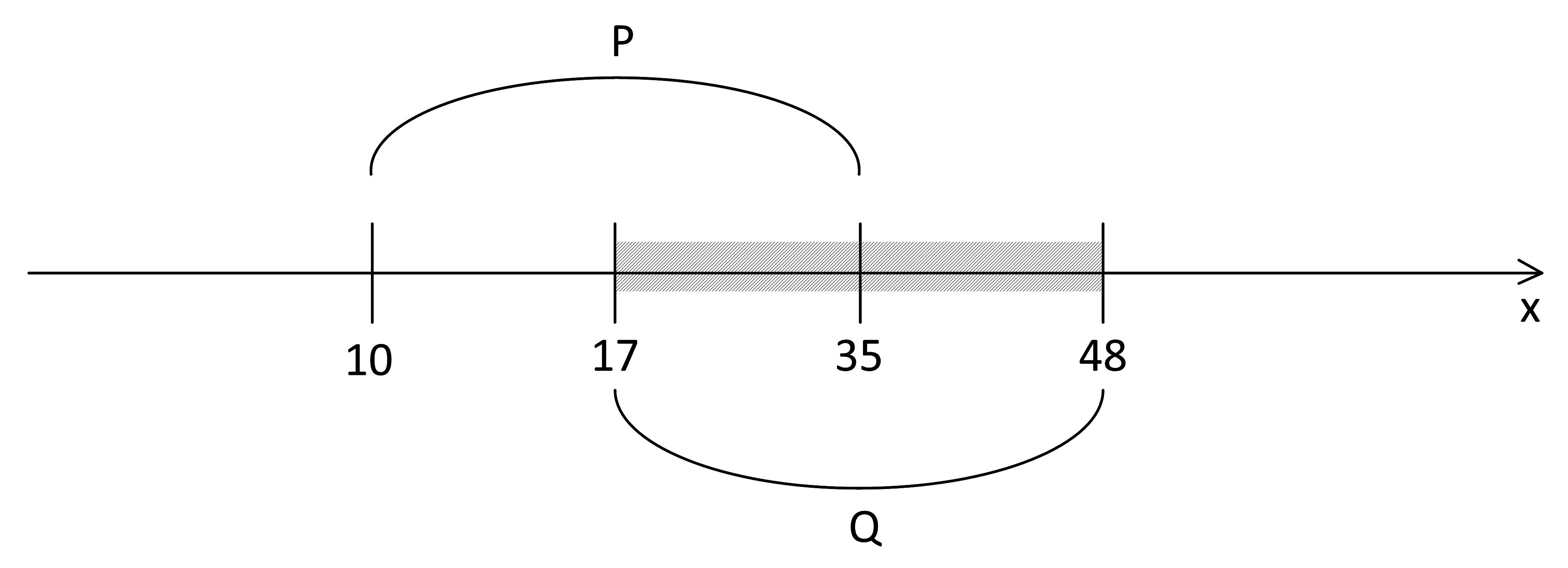
Значит, на отрезке Q от А ничего не зависит. А там может быть, а может и не быть:
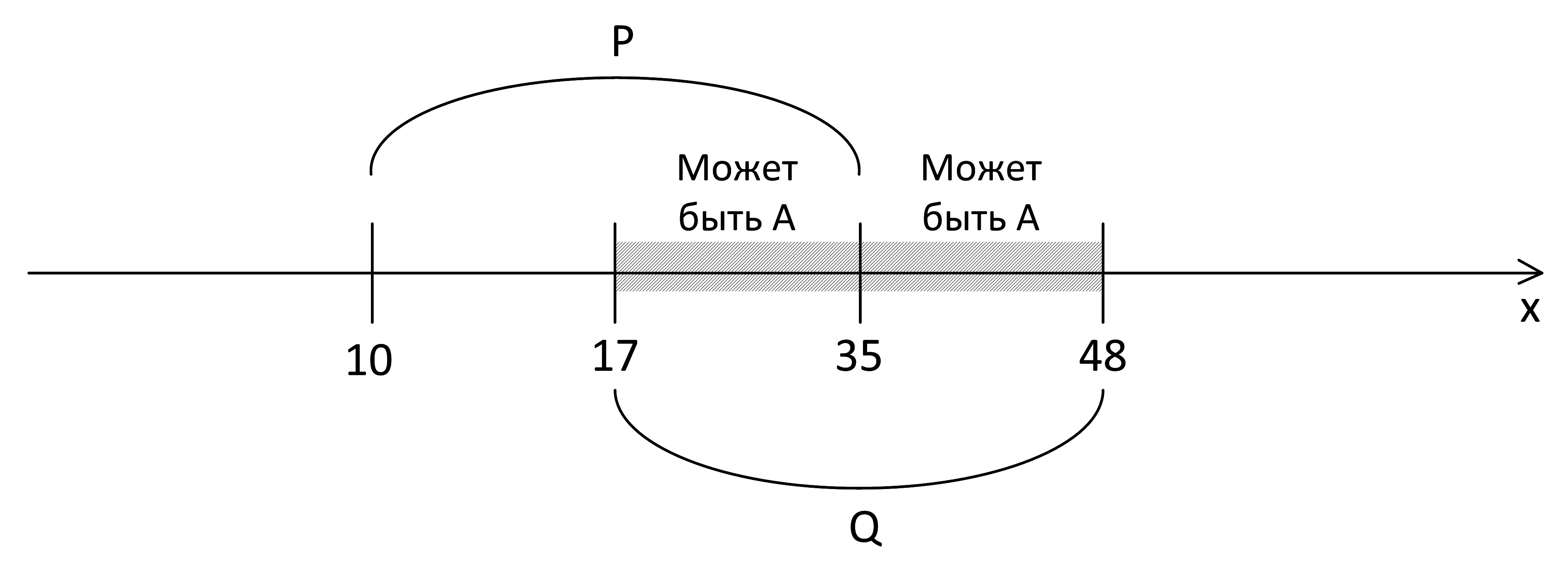
Рассмотрим точки вне всех отрезков, то есть x < 10 или x > 48.
x∈Q ложно
Так как (x∈P) ложно, то (x∈A) ∧ (x∈P) тоже ложно.
Следовательно, всё выражение будет истинным, если
¬(x∈A) – истинно,
То есть А там нет:
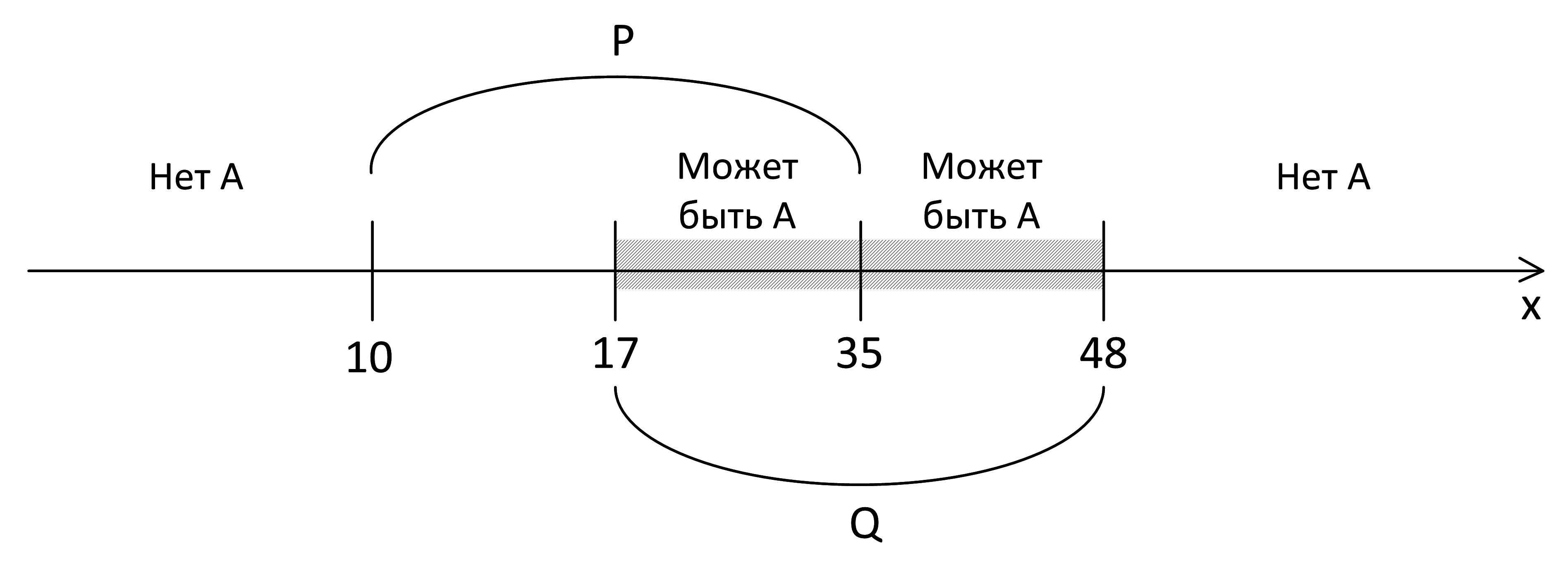
Осталось рассмотреть отрезок [10, 17].
Последнее «слагаемое» x∈Q ложно, поэтому истинным должно быть хотя бы одно из первых двух слагаемых:
- Пусть истинно второе слагаемое: ¬(x∈A) истинно, значит, А там нет:
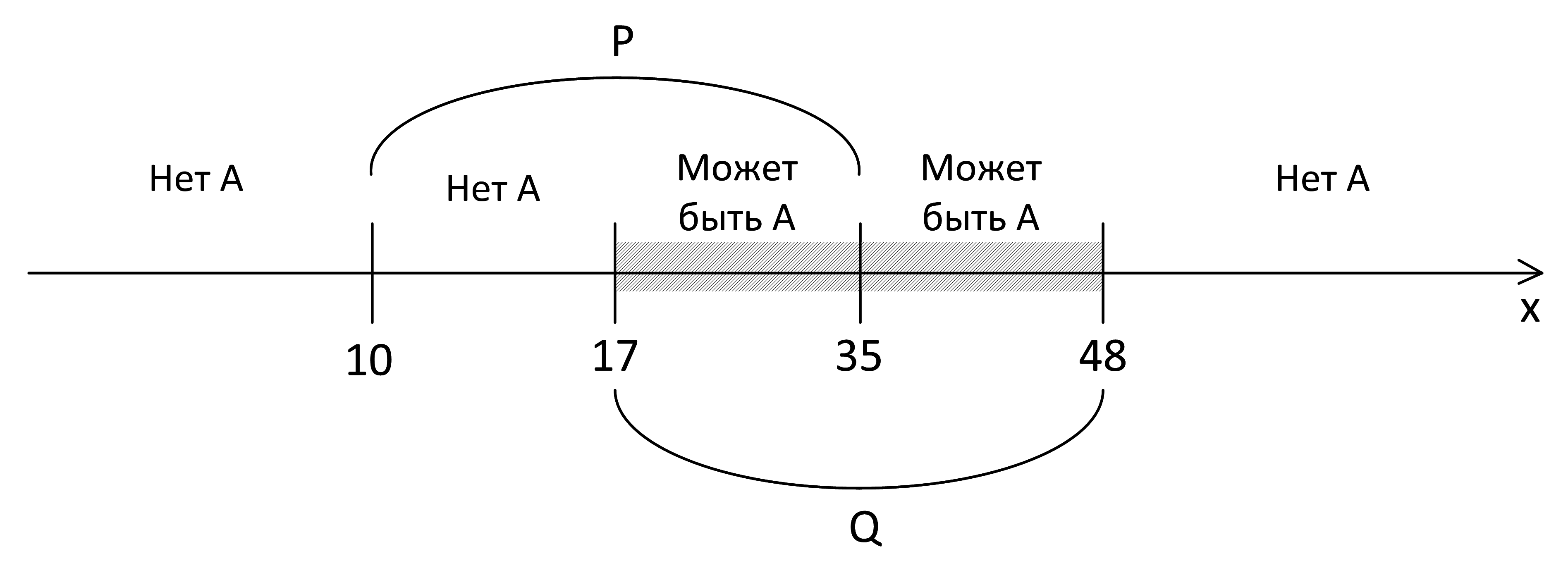
- Пусть истинно первое слагаемое: (x∈A) ∧ (x∈P). Так как это логическое умножение, то истинными должны быть оба «множителя». x∈P истинно, значит, x∈A тоже должно быть истинно:
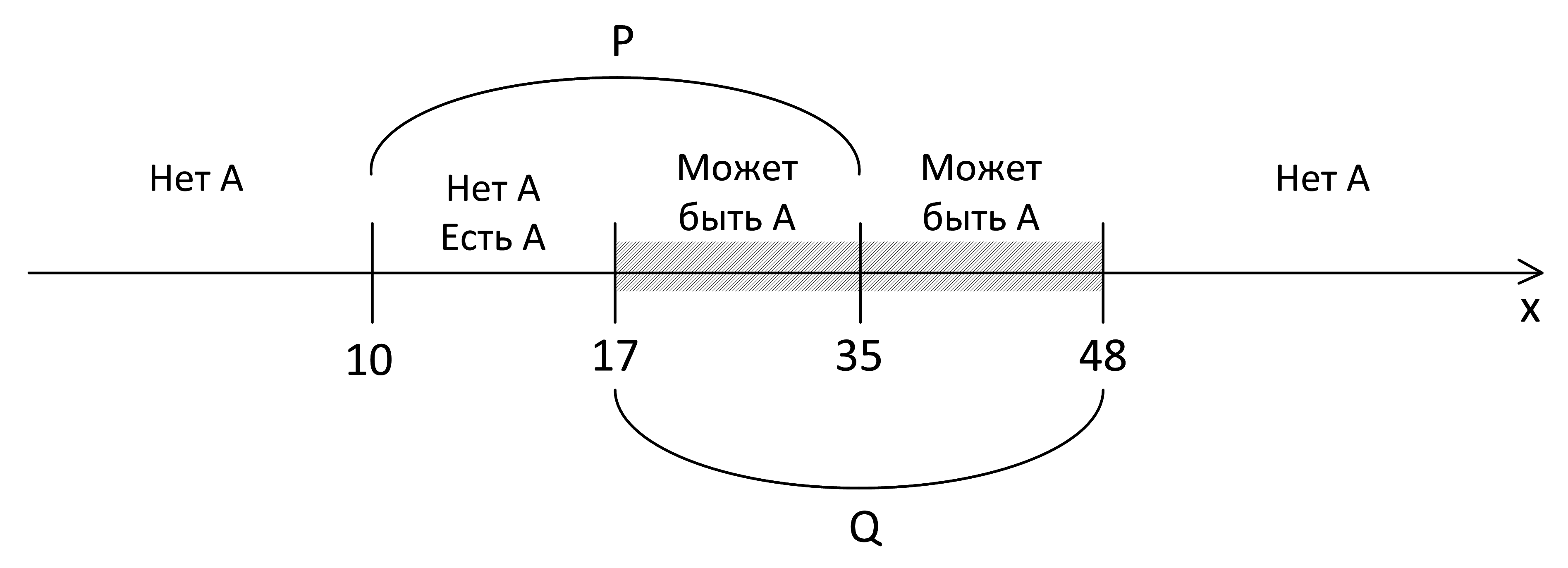
Мы получили противоречие, это означает, что на отрезке [10, 17] может быть А, а может и не быть:
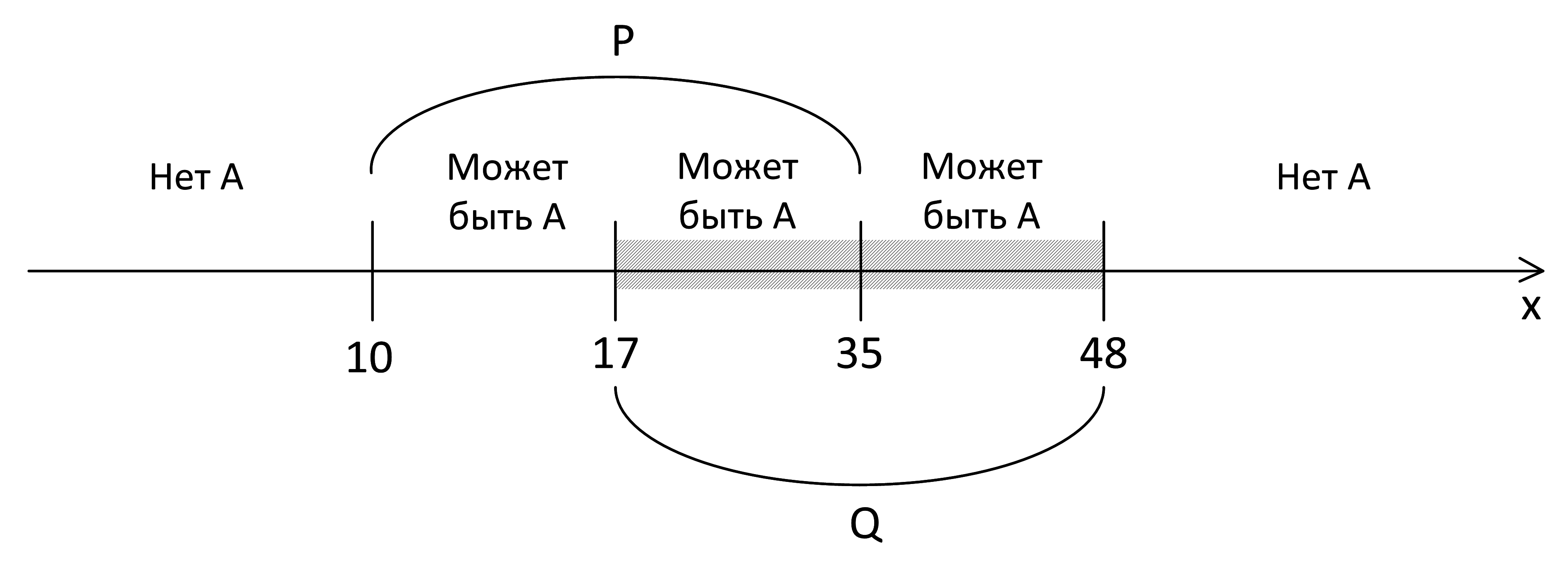
Отрезок А наибольшей длины [10, 48], его длина 48 – 10 = 38
Ответ: 38
Задача 4.2.4. На числовой прямой даны три отрезка: P = [10, 15], Q = [10, 20] и R=[5, 15]. Выберите такой интервал A, что формулы
(x∈A) → (x∈P) и (x∈Q) → (x∈R)
тождественно равны, то есть принимают равные значения при любом значении переменной х (за исключением, возможно, конечного числа точек).
1) [5, 12]
2) [10, 17]
3) [12, 20]
4) [15, 25]
Решайте, как в предыдущей задаче.
Преобразуем формулы, заменив «следование» на «или»:
¬(x∈A) V (x∈P) и ¬(x∈Q) V (x∈R)
Отметим известные отрезки на числовой оси:
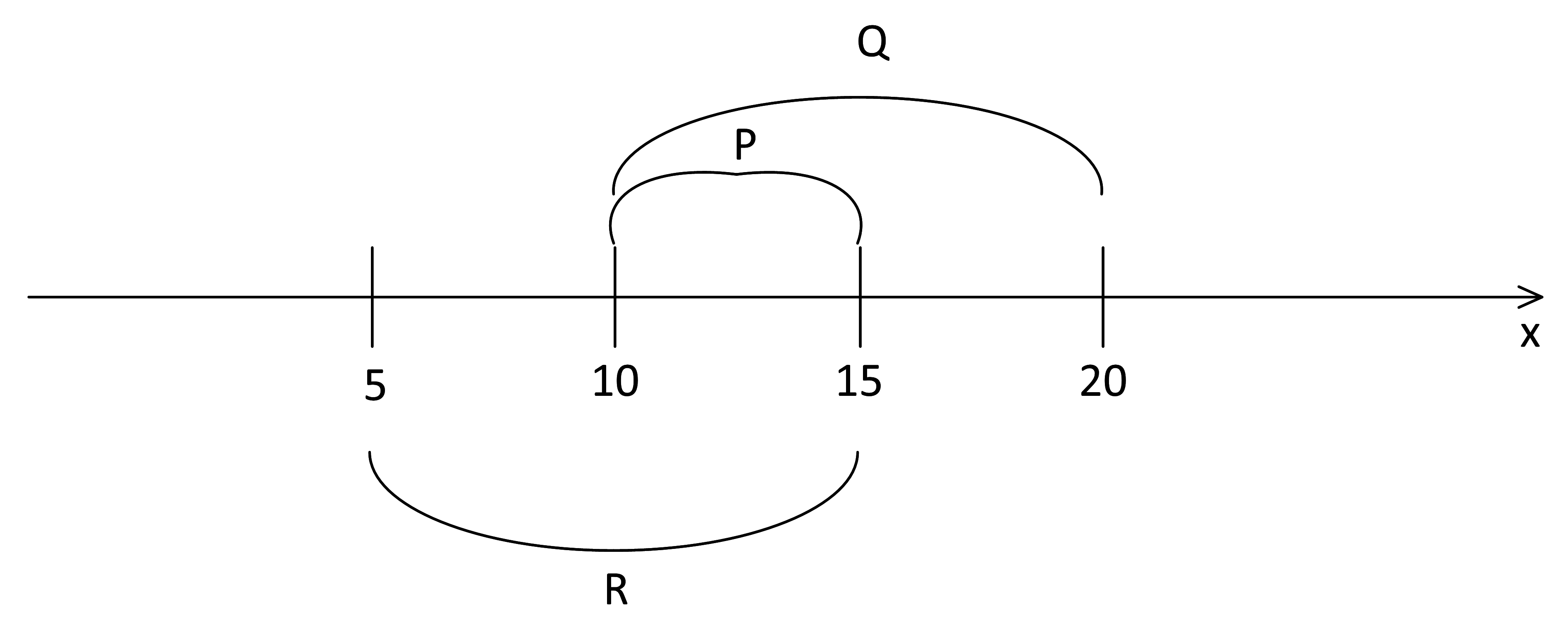
Исследуем вторую формулу. Логическое «или» истинно, когда истинно хотя бы одно из слагаемых. Следовательно, вторая формула всегда истинна вне отрезка Q:

И внутри отрезка P:
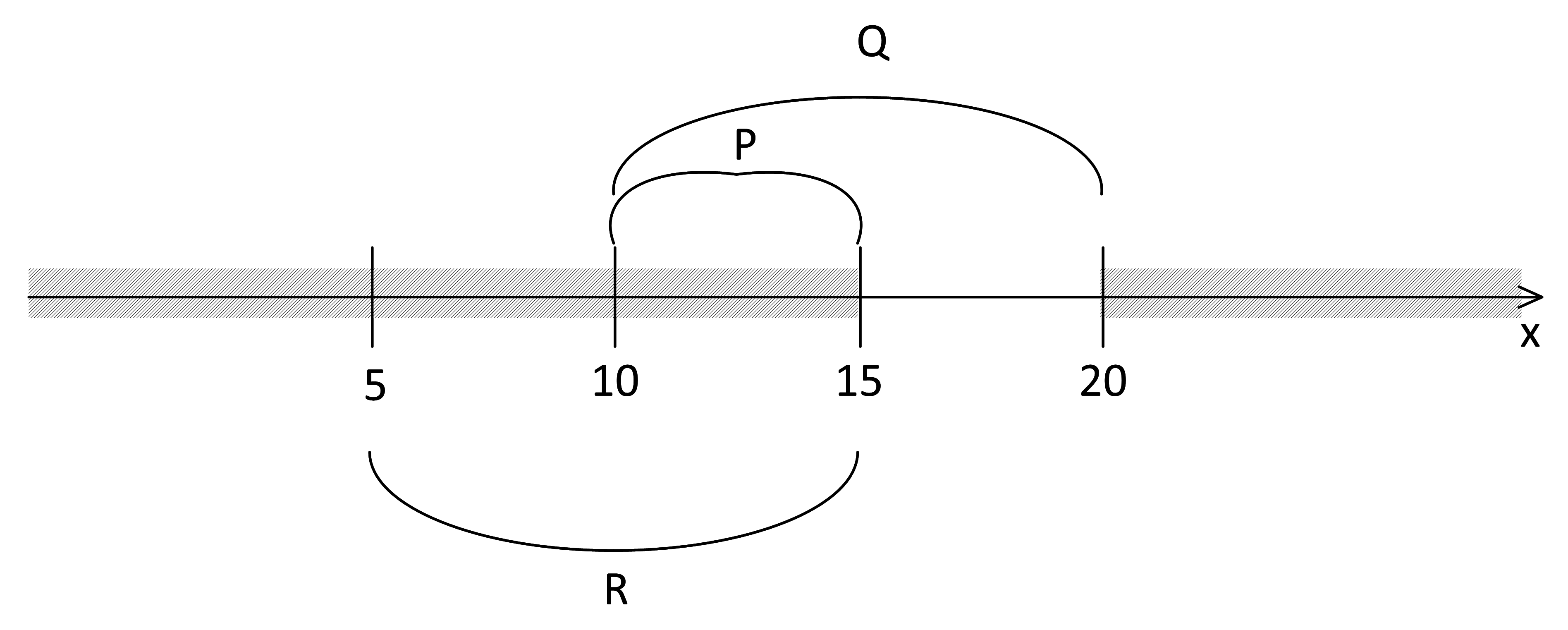
Аналогично изучим первую формулу ¬(x∈A) V (x∈P) и рассмотрим два рисунка одновременно:
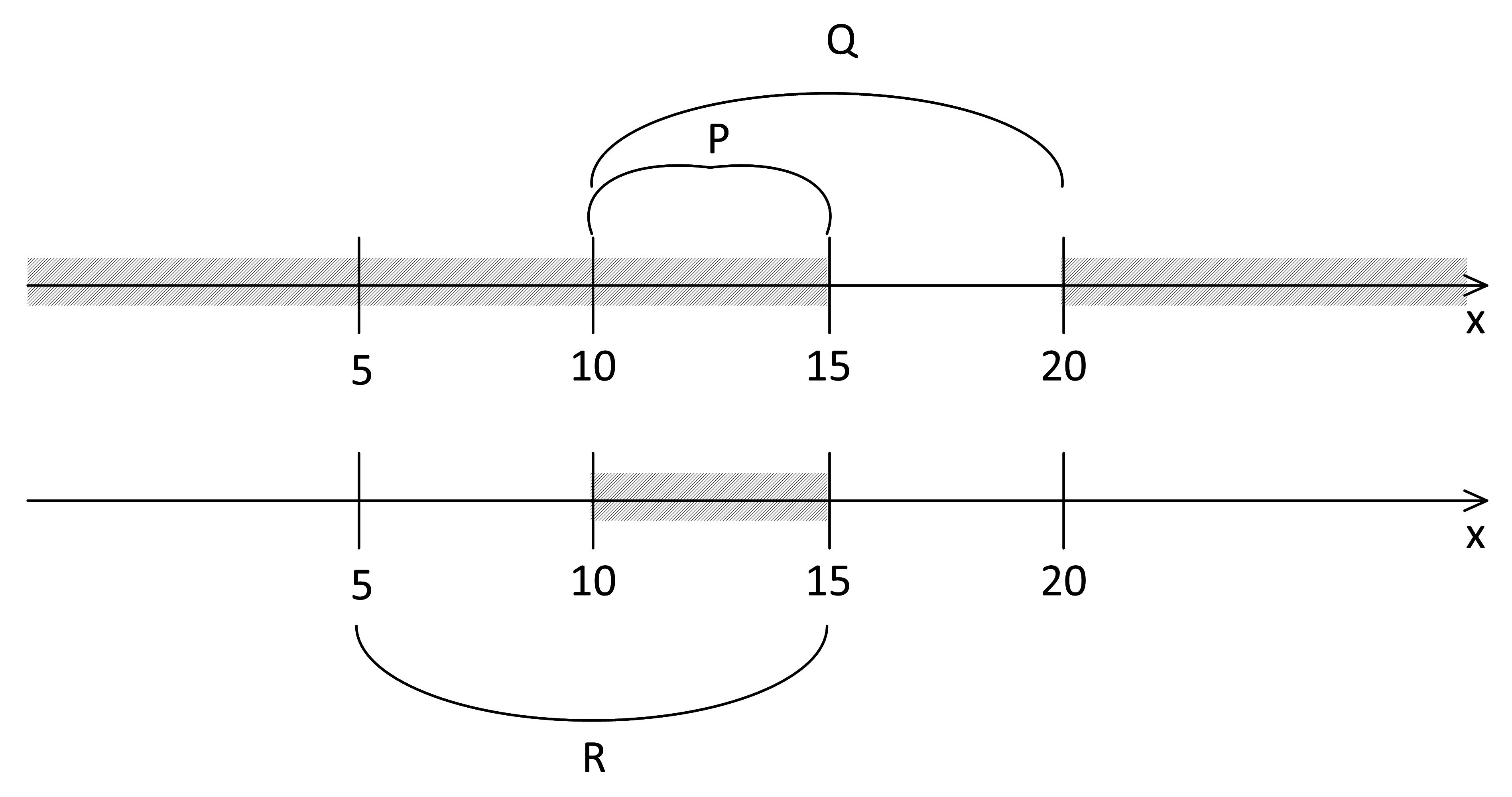
Остается расположить на оси отрезок А. На отрезке [10, 15] обе формулы истинны, поэтому от А на этом участке ничего не зависит (там может быть А). Чтобы первая формула была ложна на отрезке [15, 20], там должен быть отрезок А. При x < 10 или x > 20, чтобы первая формула была истинной, там не должно быть А:
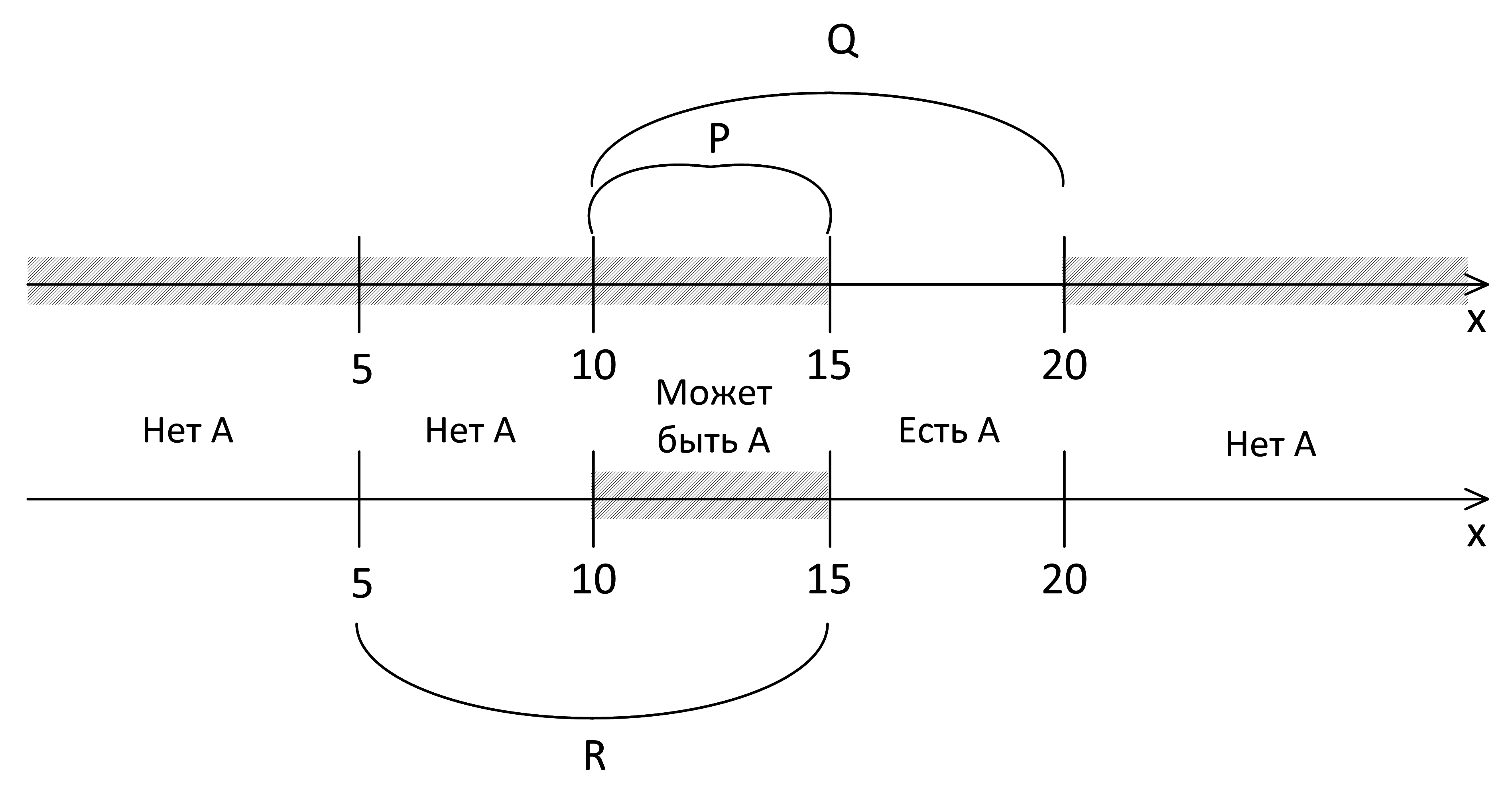
Из предложенных вариантов подходит отрезок А [12, 20].
Ответ: 3.
Задача 4.2.5. Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) → ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х. Определите наименьшее возможное значение суммы элементов множества A.
Решайте, как в предыдущей задаче, изобразив множества кругами Эйлера.
Обозначим множества буквами:
P = {2, 4, 6, 8, 10, 12},
Q = {2, 4, 6, 8, 10, 12},
Тогда выражение примет вид:
(x∈P) → (((x∈Q) ∧ ¬(x∈A)) → ¬(x∈P))
Упростим выражение, заменив следование на логическое «или»:
¬(x∈P) ∨ (¬((x∈Q) ∧ ¬(x∈A)) ∨ ¬(x∈P))
Раскроем среднюю часть по закону де Моргана:
¬(x∈P) ∨ ( (¬(x∈Q) ∨ (x∈A)) ∨ ¬(x∈P))
Слагаемое ¬(x∈P) встречается два раза, оставим только один раз и уберем лишние скобки:
¬(x∈P) ∨ ¬(x∈Q) ∨ (x∈A)
Изобразим множества кругами Эйлера. Видно, что множества имеют общие элементы:
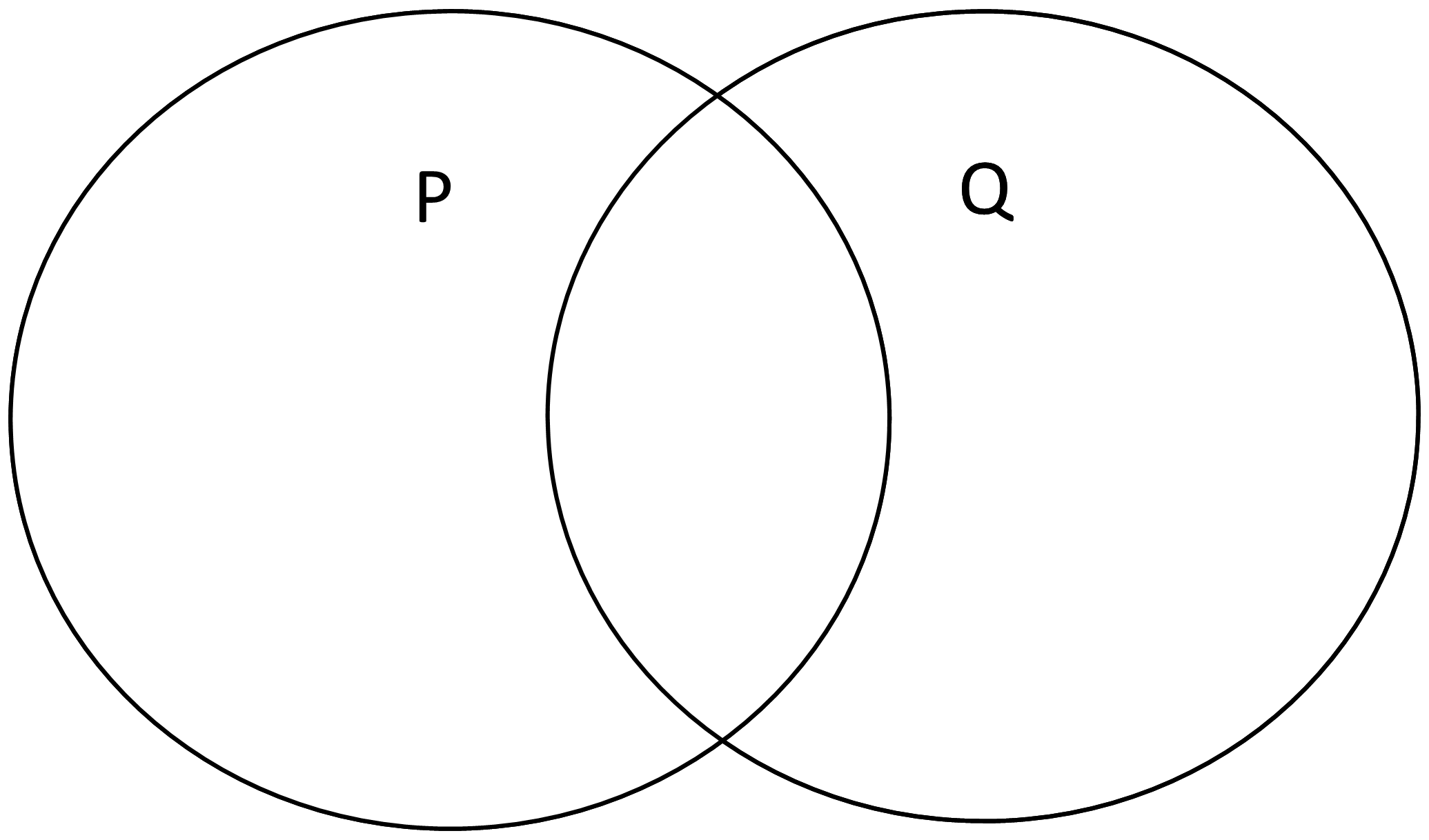
Логическое «или» истинно, когда истинно хотя бы одно из его слагаемых. «Слагаемое» ¬(x∈P) истинно вне круга P:
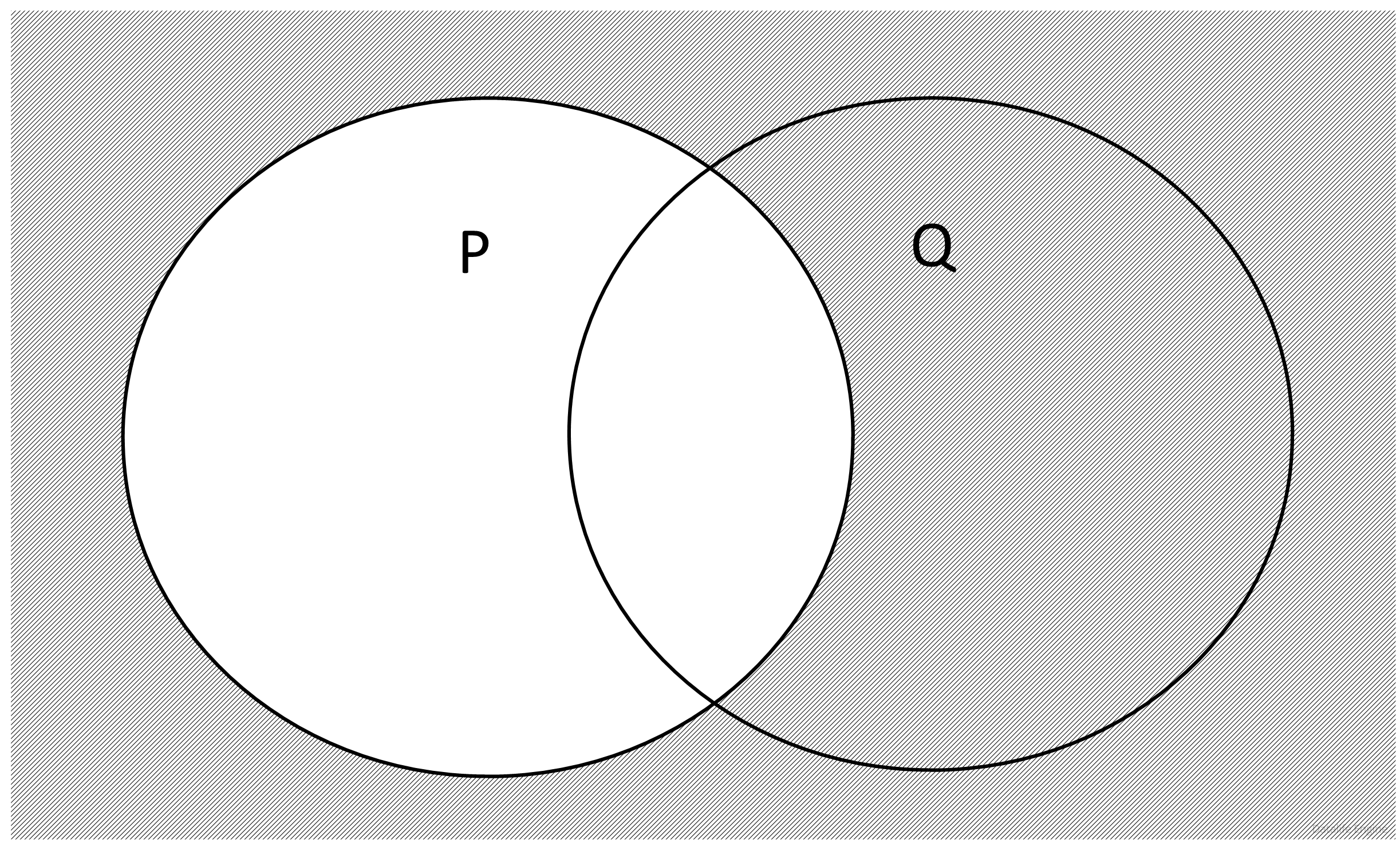
Аналогично «слагаемое» ¬(x∈Q) истинно вне круга Q:
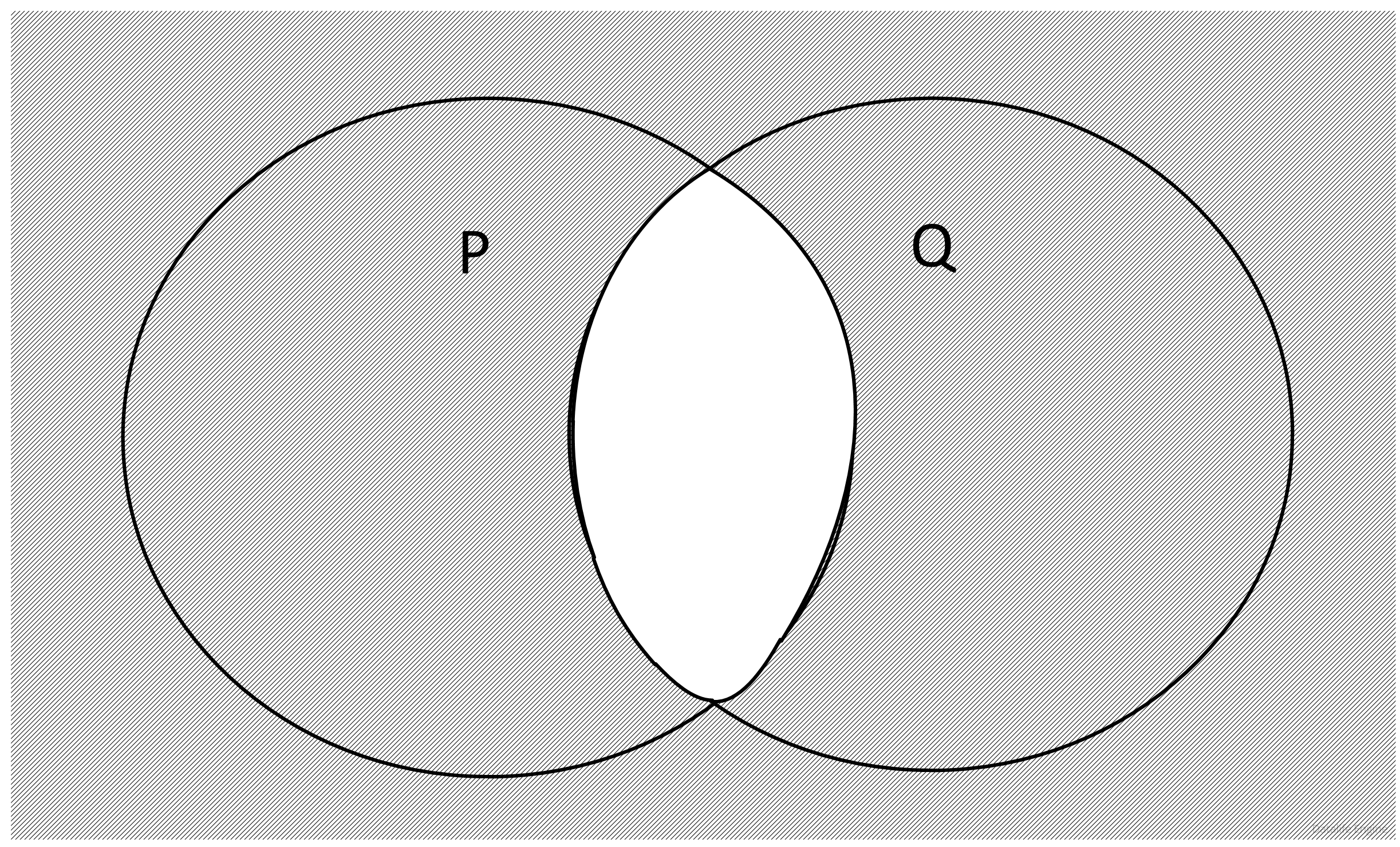
В заштрихованной области от А ничего не зависит. Следовательно, там может быть А, а может и не быть. В незаштрихованной области истинным должно быть «слагаемое» x∈A, то есть А там должно находиться:
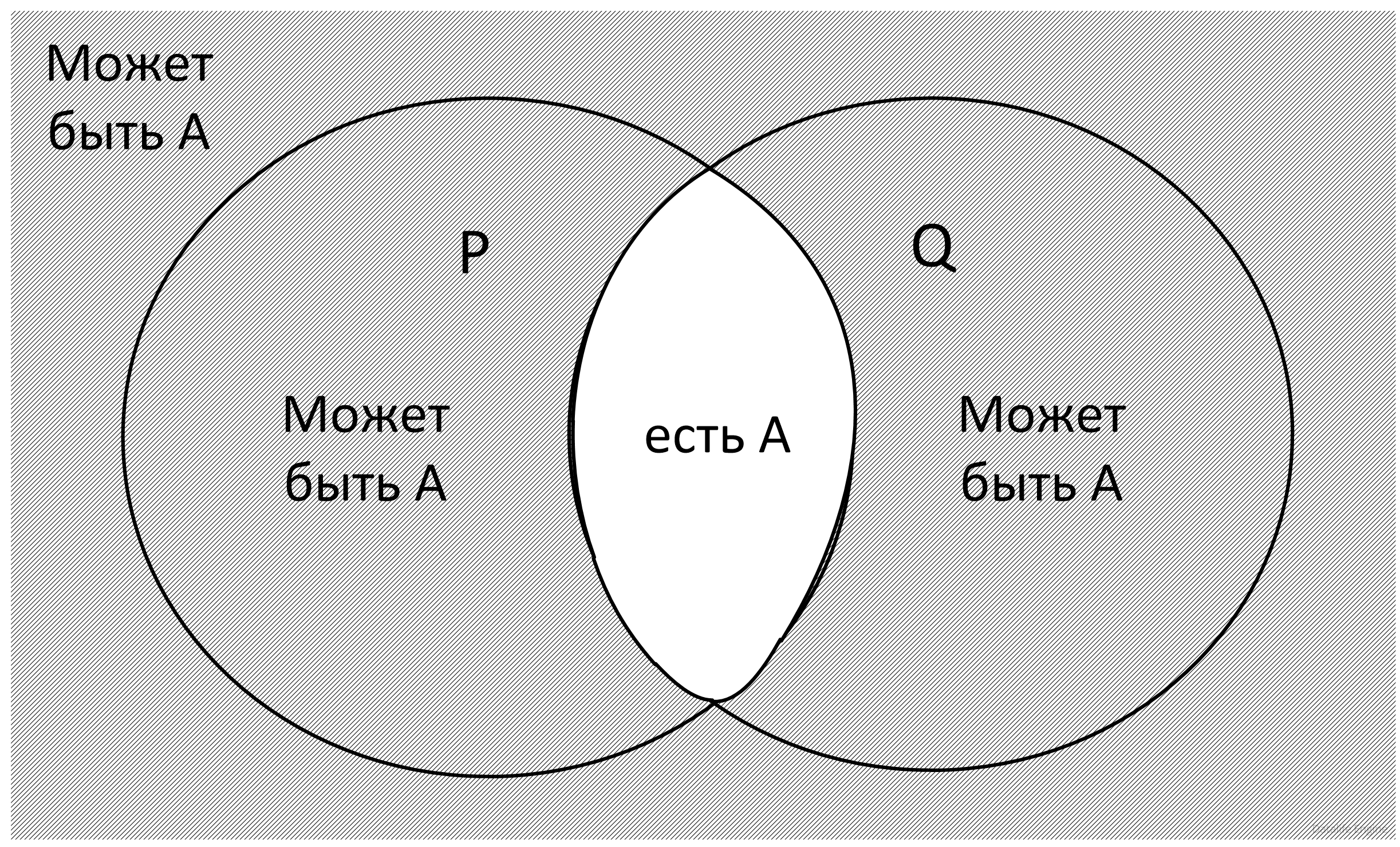
Следовательно, минимально возможное А состоит из общих элементов множеств Р и Q:
A = {6, 12}
Сумма элементов 6 + 12 = 18
Ответ: 18
Примечание. В этой задаче мы впервые воспользовались удобным инструментом для задач о множествах – кругами Эйлера. Мы еще встретимся с ними в следующем параграфе – в задачах на поисковые запросы в интернете и электронные таблицы.
Задача 4.2.6. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа числа А формула
¬ДЕЛ (x, A) → (ДЕЛ (x, 6) → ¬ДЕЛ (x, 4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Начинайте упрощать, как в предыдущих задачах, но на этом не останавливайтесь и преобразуйте выражение до тех пор, пока не сможете осмысленно прочитать его на естественном языке.
В выражении
¬ДЕЛ (x, A) → (ДЕЛ (x, 6) → ¬ДЕЛ (x, 4))
заменим следование на логическое «или»:
ДЕЛ (x, A) ∨ (¬ДЕЛ (x, 6) ∨ ¬ДЕЛ (x, 4))
По закону де Моргана вынесем отрицание за общую скобку в последних двух «слагаемых»:
ДЕЛ (x, A) ∨ ¬ ((ДЕЛ (x, 6) ∧ ДЕЛ (x, 4))
Переставим «слагаемые» местами:
¬ ((ДЕЛ (x, 6) ∧ ДЕЛ (x, 4)) ∨ ДЕЛ (x, A)
Заменим логическое «или» на следование:
((ДЕЛ (x, 6) ∧ ДЕЛ (x, 4)) → ДЕЛ (x, A)
А теперь прочитаем это выражение на естественном языке:
Если x делится на 6 и x делится на 4, то x делится на …
Что вы поставите вместо многоточия?
Ошибка. Вы будете не правы, если ответите 6 * 4 = 24. Потому что есть число 12, которое тоже делится и на 6, и на 4.
Продолжение хода решения.
Ответом будет наименьшее общее кратное НОК(6, 4) = 12. Если вы забыли, как оно вычисляется, посмотрите задачу на системы счисления 1.2.11, в которой мы уже встречались с НОК.
Из прошлой задачи мы получили новый инструмент для вычисления НОК – круги Эйлера:
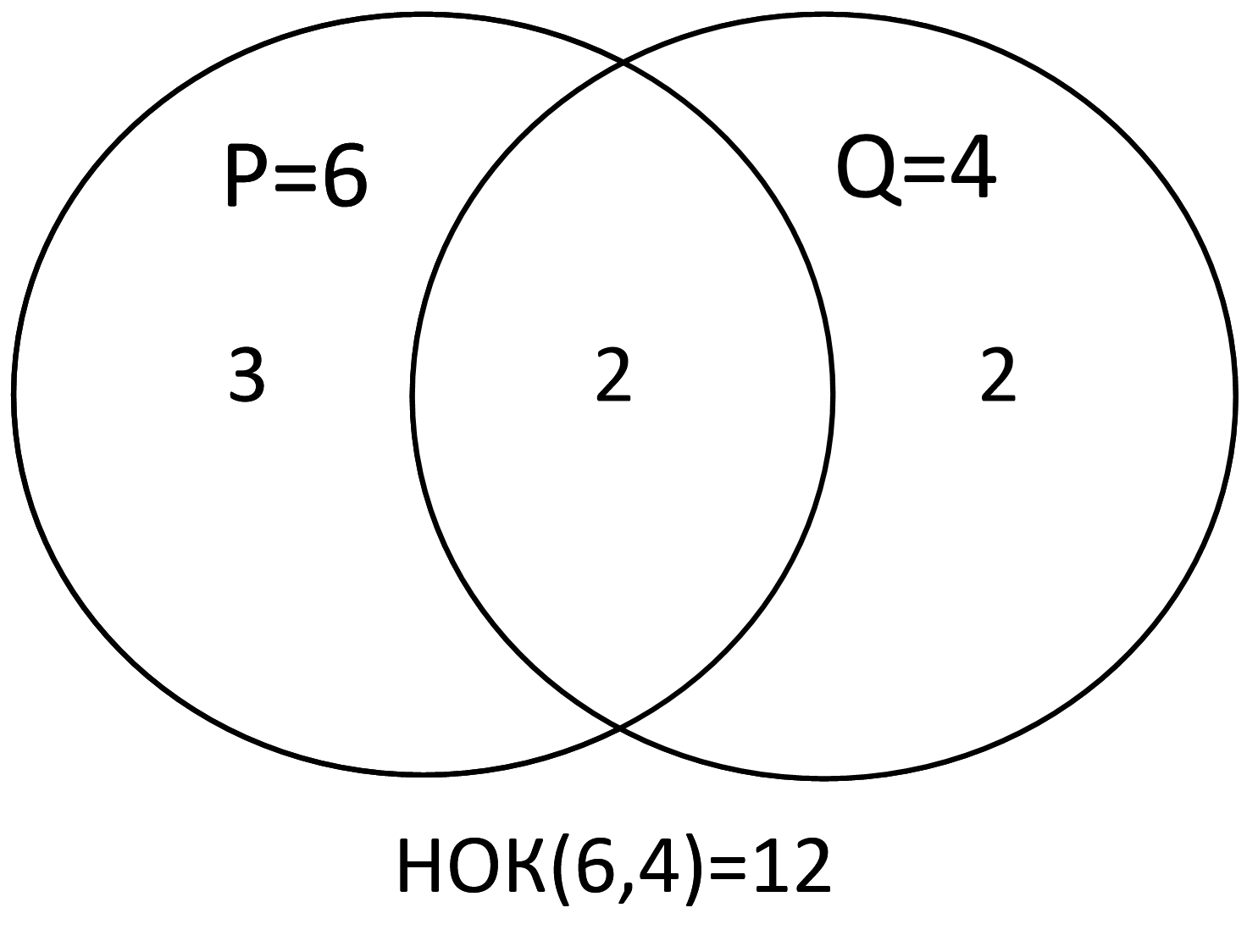
Ответ: 12
Модификация задачи.
Предположим, после упрощения у нас получилось выражение:
((ДЕЛ (x, 6) ∨ ДЕЛ (x, 4)) → ДЕЛ (x, A)
Для какого наибольшего натурального числа А формула тождественно истинна?
В модифицированной задаче логическое «и» заменили на логическое «или».
Прочитаем выражение на естественном языке:
Если x делится на 6 или x делится на 4, то x делится на …
Что вы поставите вместо многоточия?
Ответом будет наибольший общий делитель НОД(6, 4) = 2.
В задаче 1.5.4 мы уже сталкивались с НОД, поэтому, если вы забыли, что это такое, повторите эту задачу. НОД также можно вычислить с помощью кругов Эйлера:
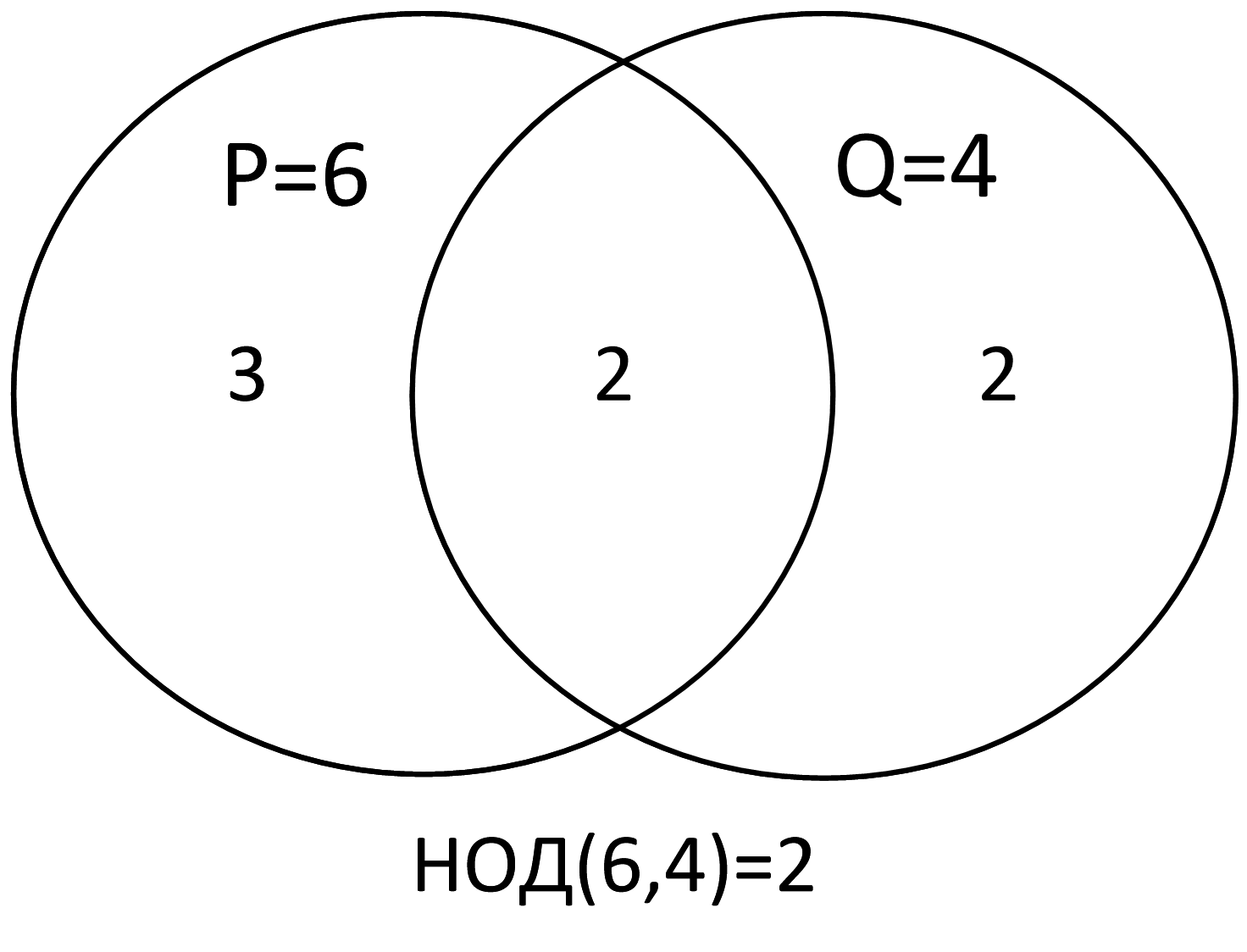
Задача 4.2.7. Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4
Для какого наименьшего неотрицательного целого числа А формула
x & 25 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Это задача на стыке двух тем – логики и систем счисления. Переведите числа в двоичную систему, замените следование на логическое «или». Подберите примеры таких x, при которых каждое «слагаемое» ложно. Затем сделайте неизвестные биты в x наиболее неудобными для А. Далее подберите А.
Переведем числа в двоичную систему:
|
25
|
2
|
|
|
|
17
|
2
|
|
|
|
|
1
|
12
|
2
|
|
|
1
|
8
|
2
|
|
|
|
|
0
|
6
|
2
|
|
|
0
|
4
|
2
|
|
|
|
|
0
|
3
|
2
|
|
|
0
|
2
|
2
|
|
|
|
|
1
|
1
|
|
|
|
0
|
1
|
Выражение в двоичном виде примет вид:
x & 11001 ≠ 0 → (x & 10001 = 0 → x & А ≠ 0)
Заменим следование на логическое «или»:
X & 11001 = 0 ∨ x & 10001 ≠ 0 ∨ x & А ≠ 0
Построим наиболее «неудобный» пример х, при котором «слагаемые» будут ложными. Рассмотрим первое «слагаемое»:
x & 11001 = 0
Чтобы оно было ложным, в вводимом x достаточно, чтобы один из битов на тех местах, где в 11001 находятся «1», также была «1»:
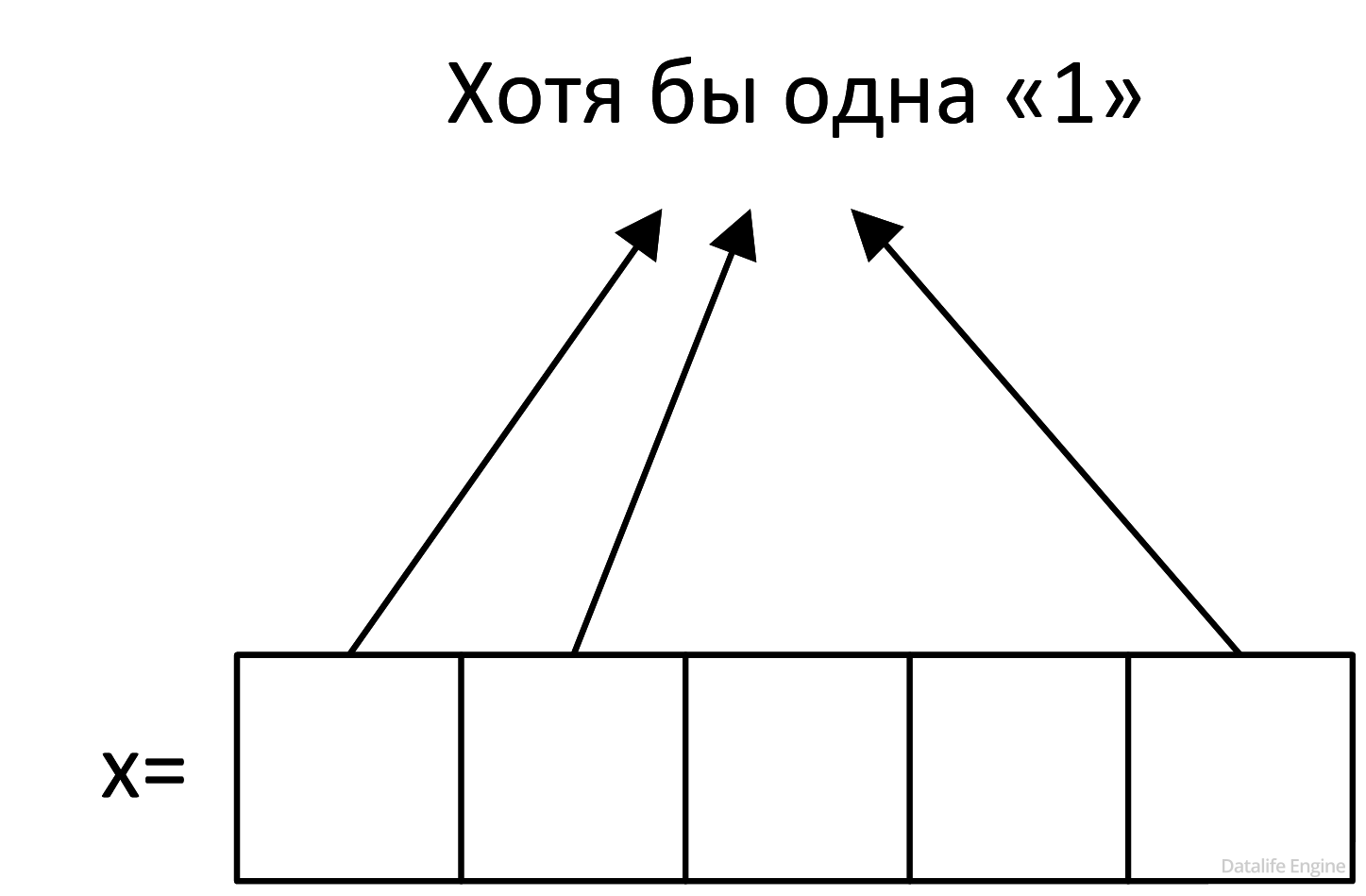
Рассмотрим второе «слагаемое»: x & 10001.
Чтобы оно было ложным, надо, чтобы в х на тех местах, где в 10001 стоят «1», были нули. Продолжим заполнять наш рисунок:
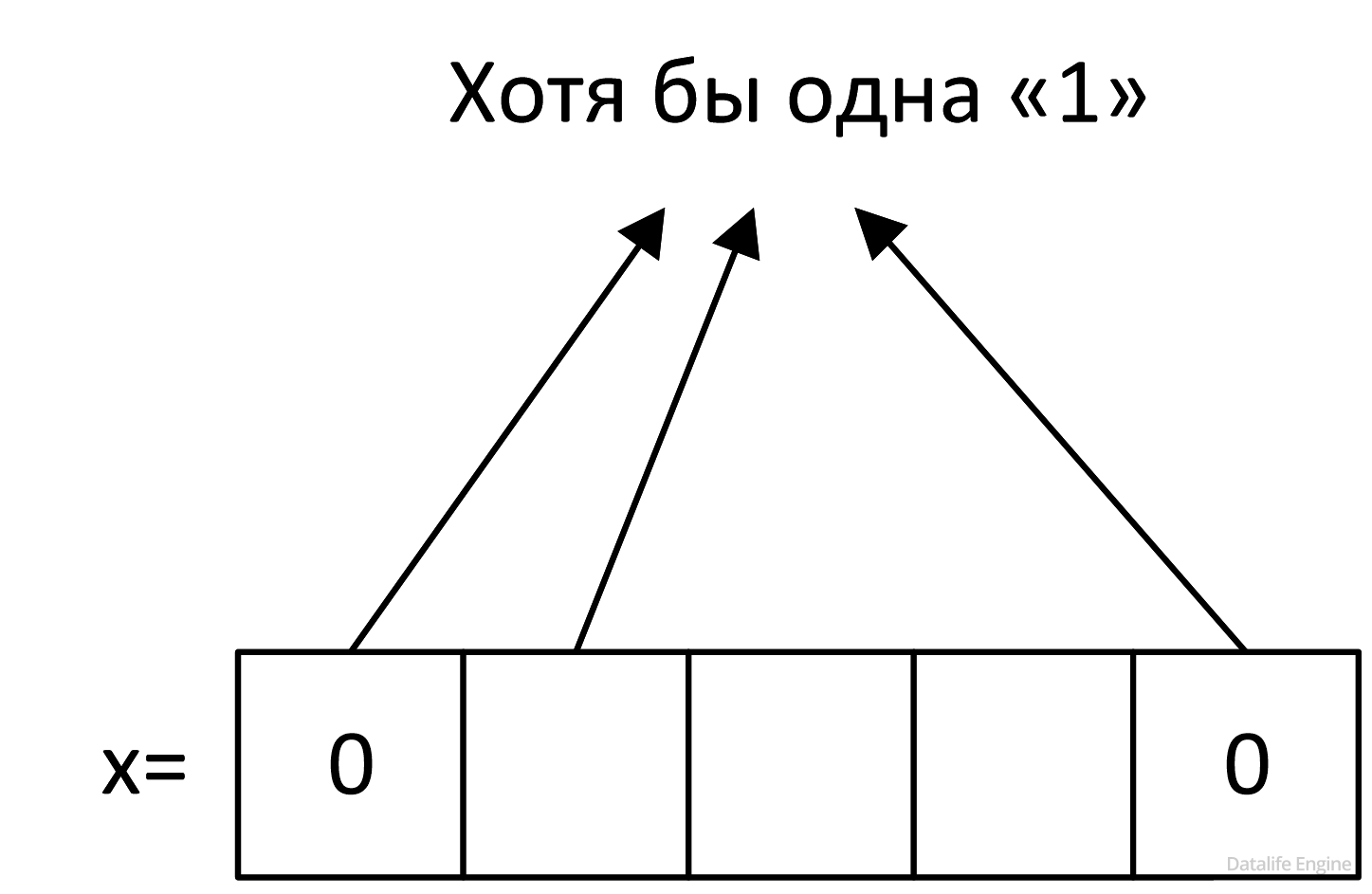
Убираем лишние стрелочки:
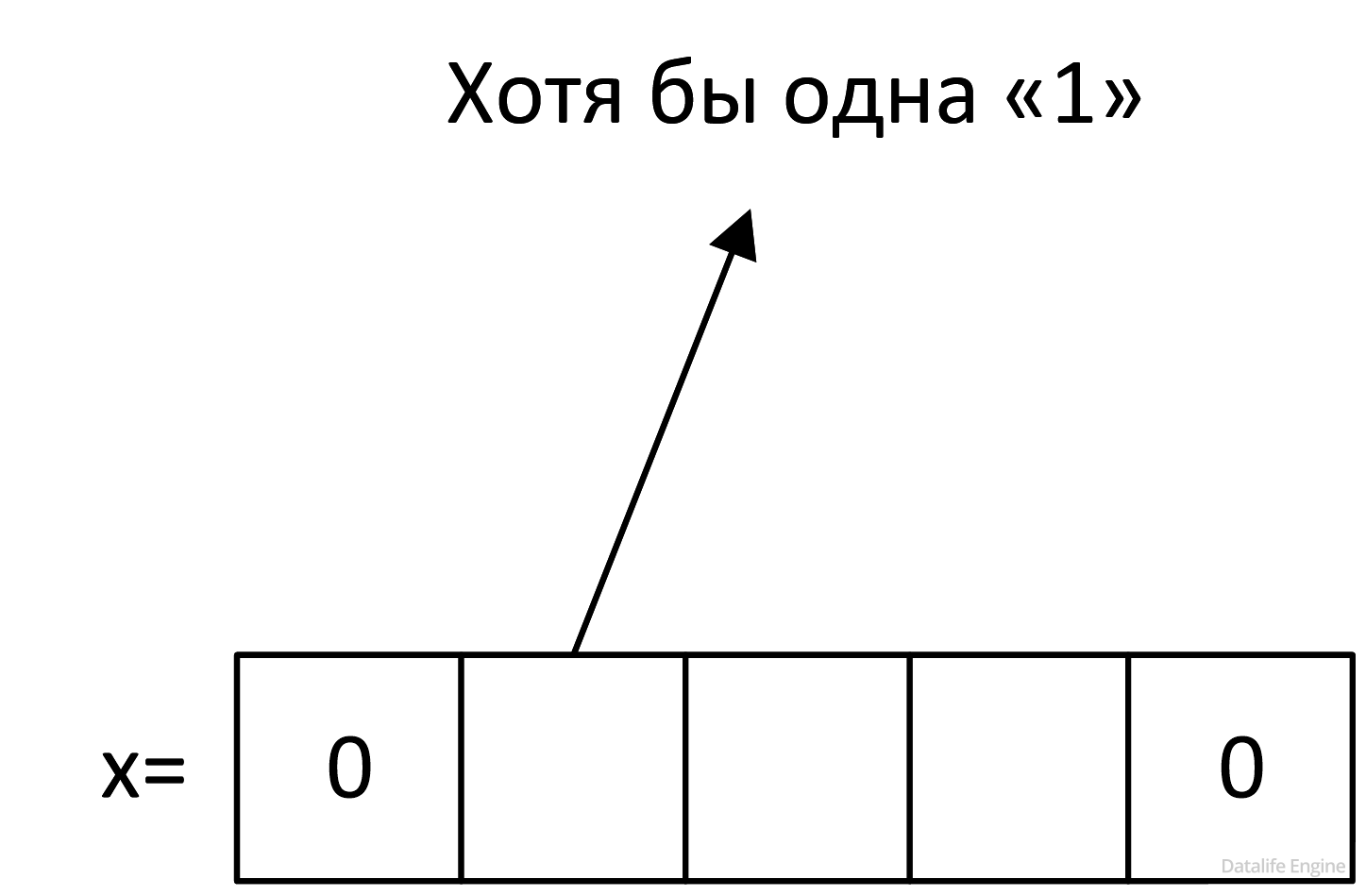
И тогда мы можем заполнить x уже более определенно:

Рассмотрим третье «слагаемое» x & А ≠ 0.
Напомню, мы ищем наиболее «вредный» пример x, превращающий слагаемые в ложь. Чтобы увеличить шансы обращения третьего слагаемого в 0, заполним оставшиеся биты нулями:

Мы нашли проблемный x, при котором первые два слагаемых ложны. Значит, при нем должно быть истинно третье слагаемое. Нужно, чтобы в результате действия третьего слагаемого мы получили ненулевой ответ:
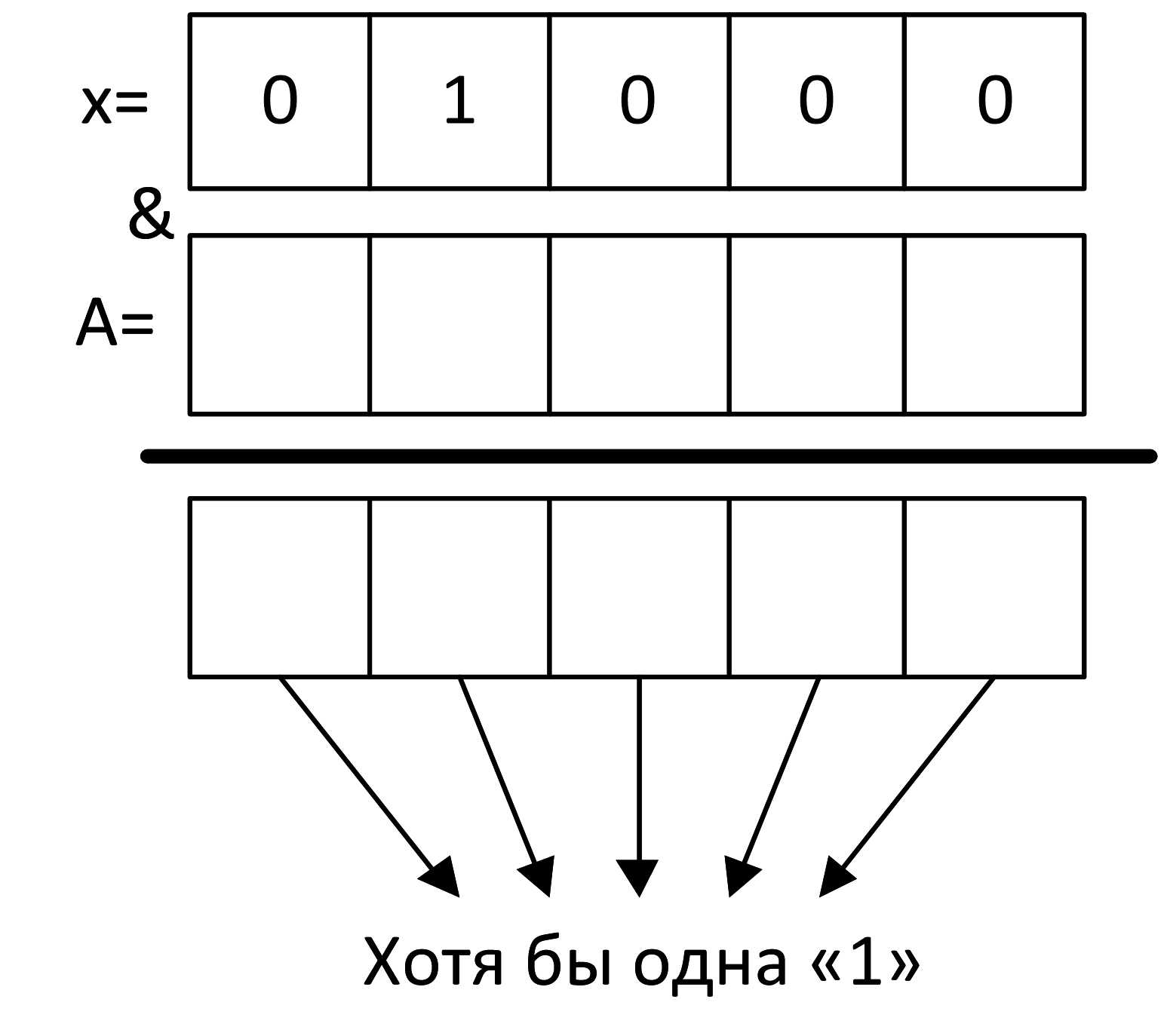
Под нулями может идти что угодно, это не повлияет на результат:
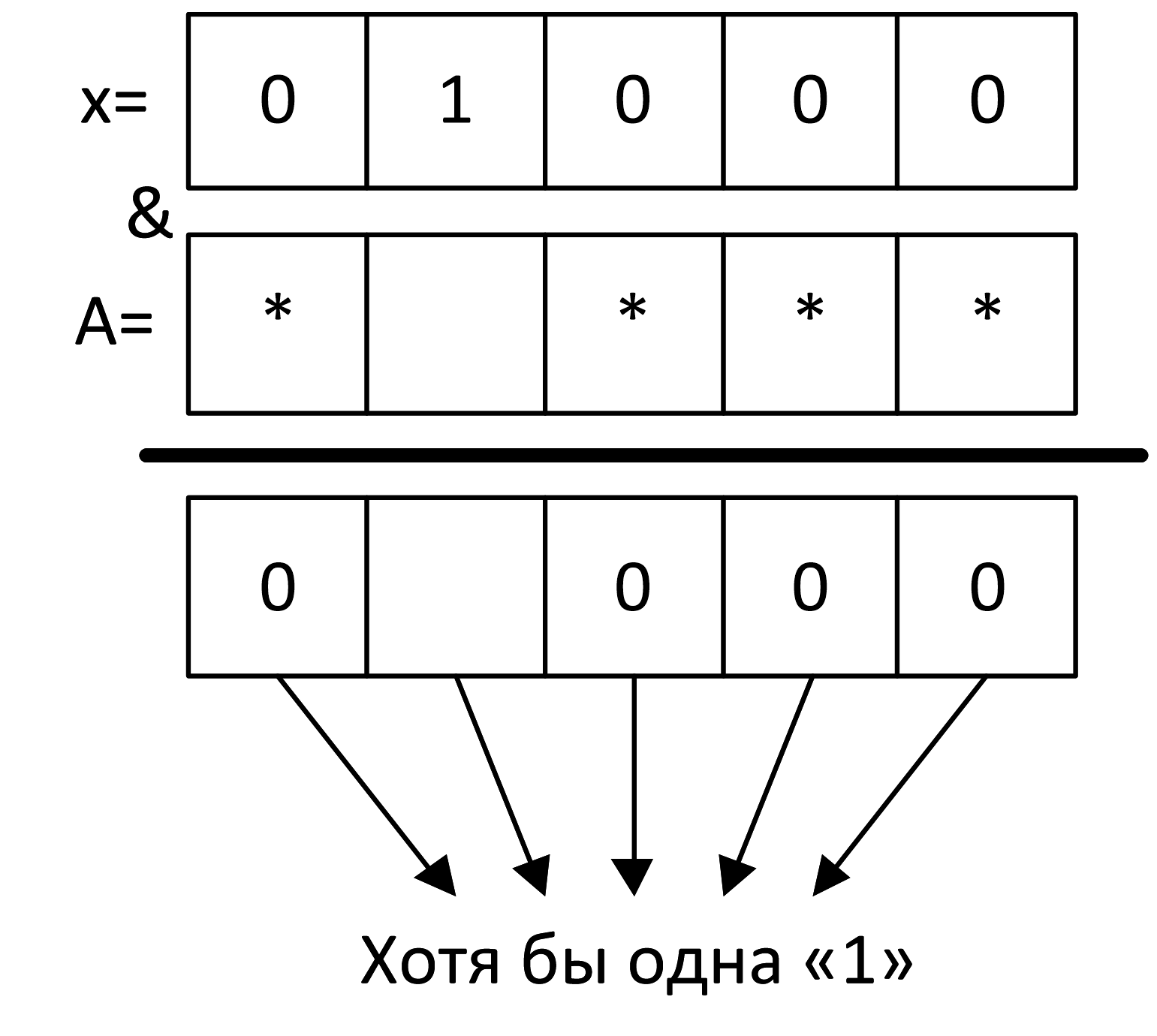
Убираем лишние стрелочки:
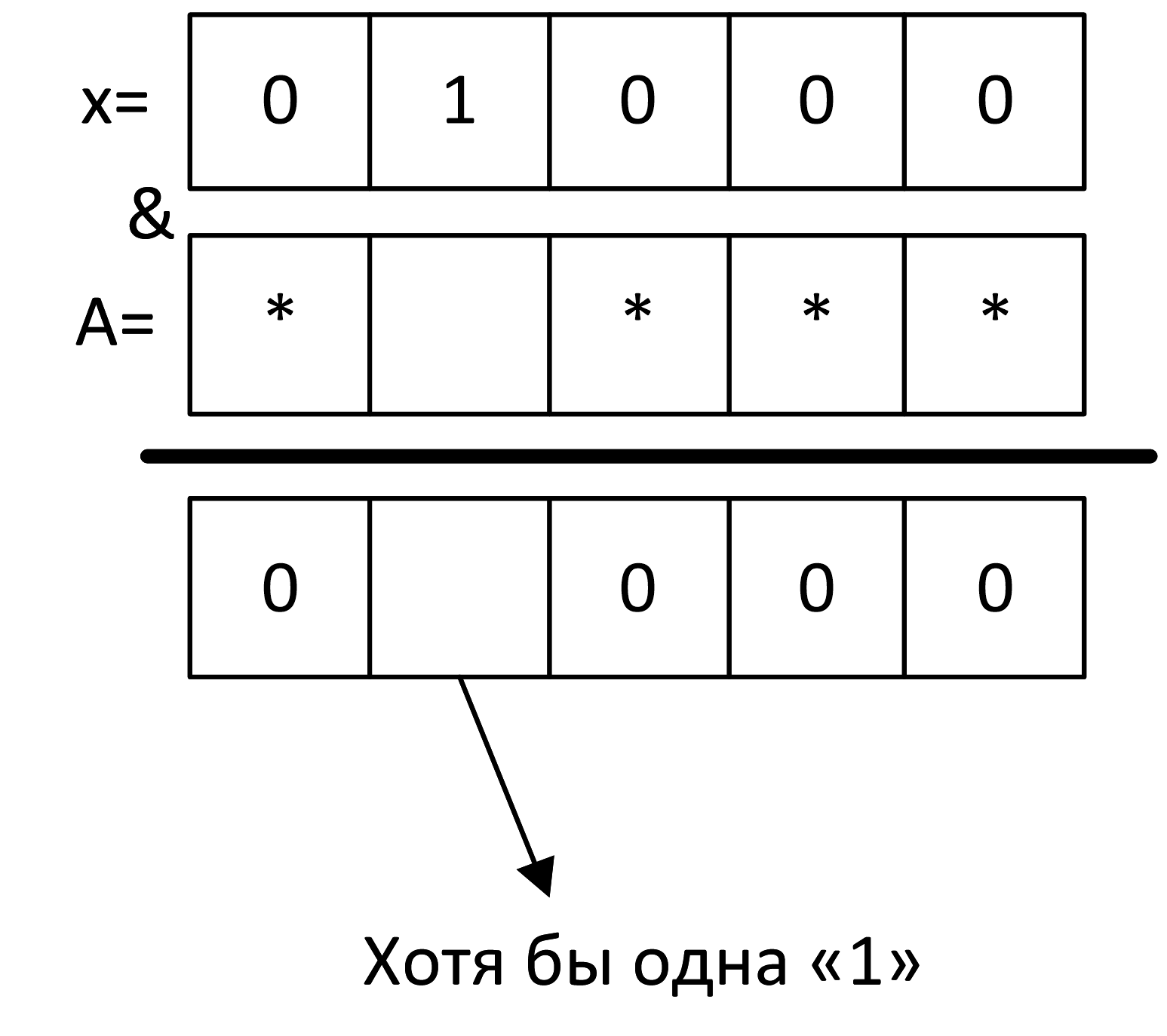
Следовательно:
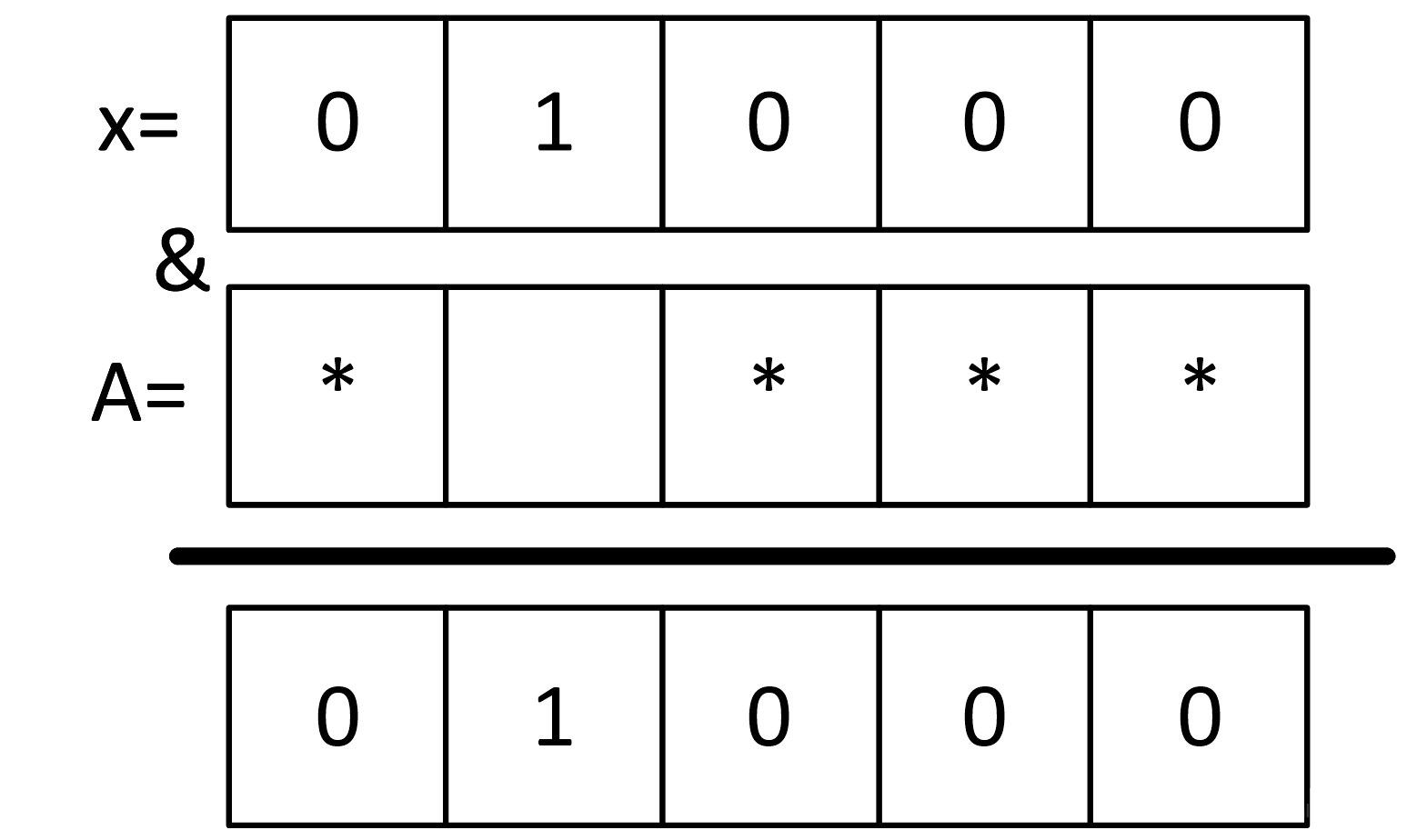
Заполняем последний бит шаблона А:
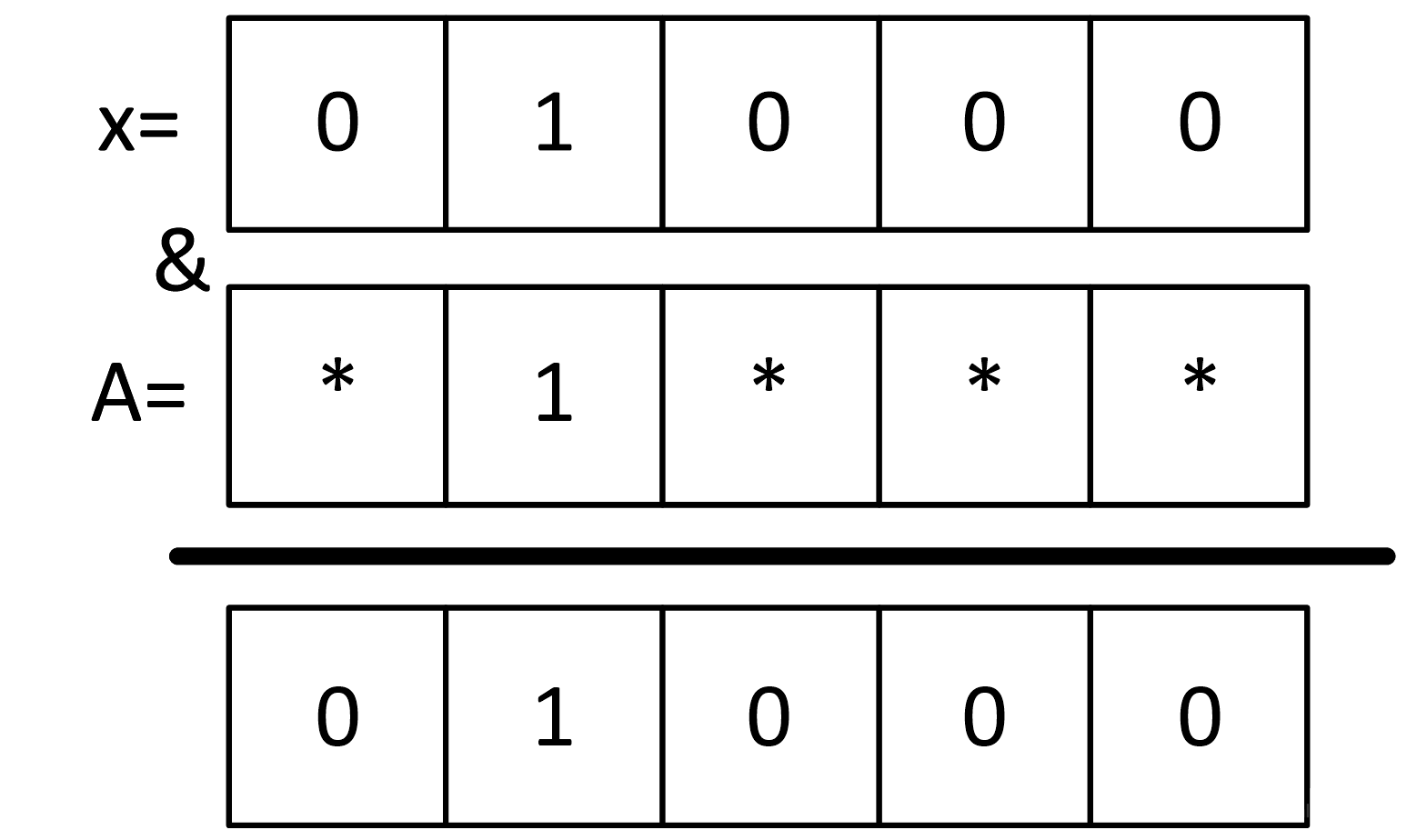
Мы получили тот же самый шаблон, что и при вспомогательных действиях.
Поскольку мы ищем минимальное А, то
А = *1*** = 01000 = 8
Ответ: 8
Задача 4.2.8. Для какого наибольшего целого числа А формула
x & 51 = 0 ∨ (x & 41 = 0 → x & А = 0)
тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
Переведем десятичные числа в двоичную систему:
x & 110011 = 0 ∨ (x & 101001 = 0 → x & ????? = 0)
Заменим «следование» на логическое «или»:
x & 110011 = 0 ∨ x & 101001 ≠ 0 ∨ x & ????? = 0
Так же, как и в предыдущей задаче, будем искать наиболее проблемное x, при котором все «слагаемые» ложны.
Рассмотрим первое «слагаемое»:
x & 110011 = 0
Чтобы оно было ложно, мы должны получить ответ, отличный от нуля. Это возможно, когда на месте единичек в 110011 будет стоять хотя бы одна единичка в х:
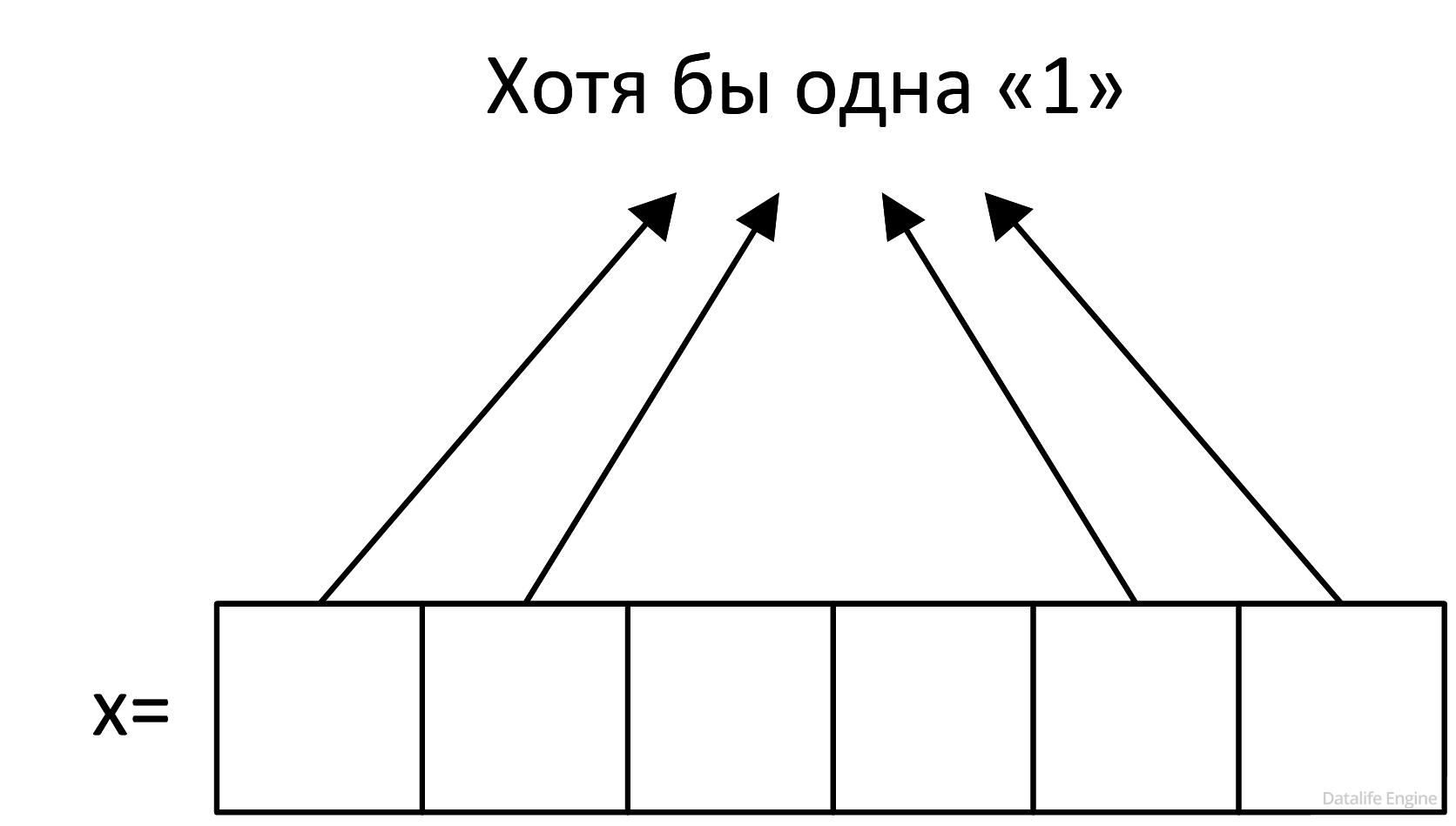
Рассмотрим второе «слагаемое»:
x & 101001 ≠ 0
Чтобы оно было ложным, на месте единичек в 101001 в переменной х должны идти одни нули:
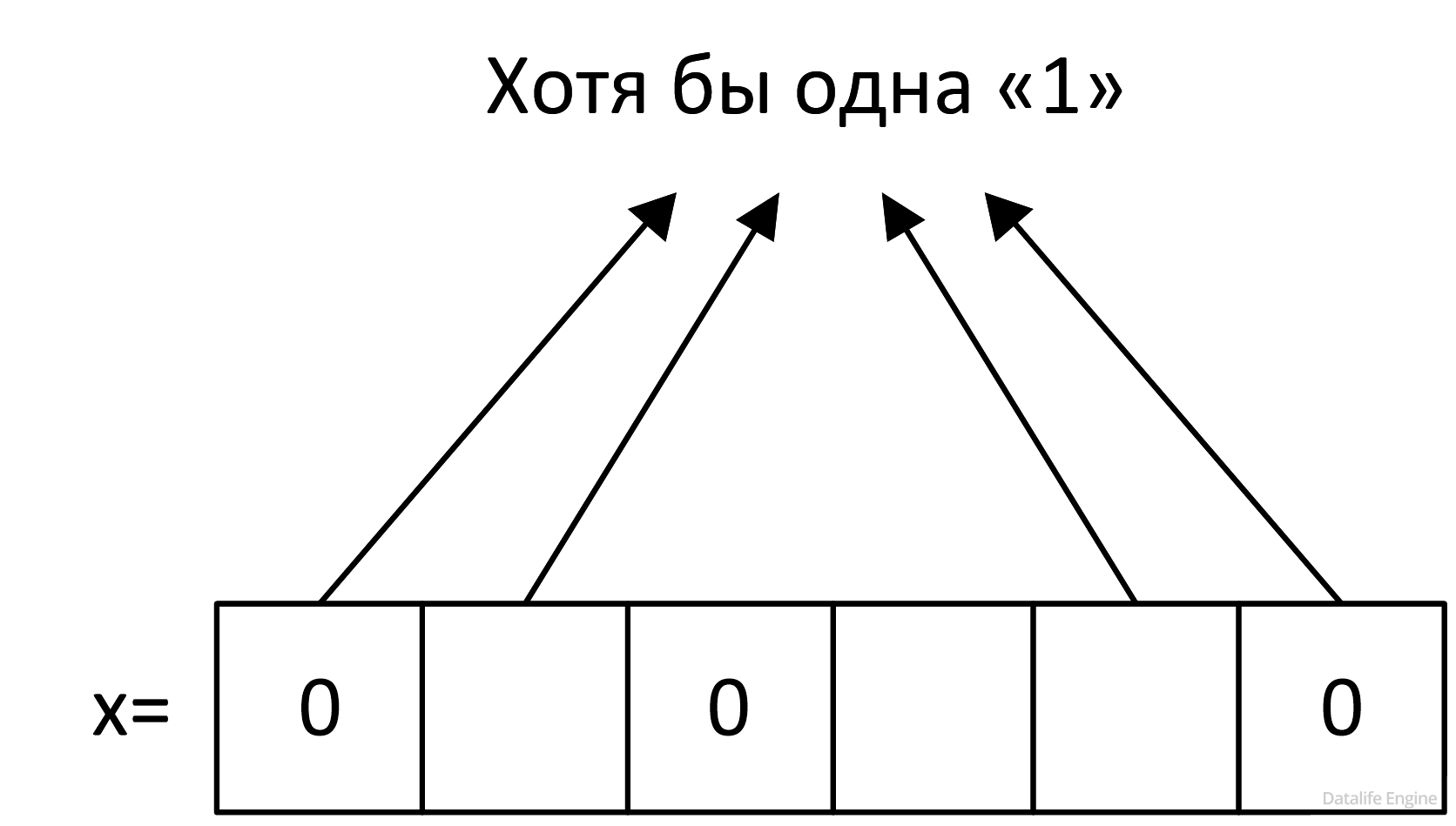
Ликвидируем лишние стрелочки:
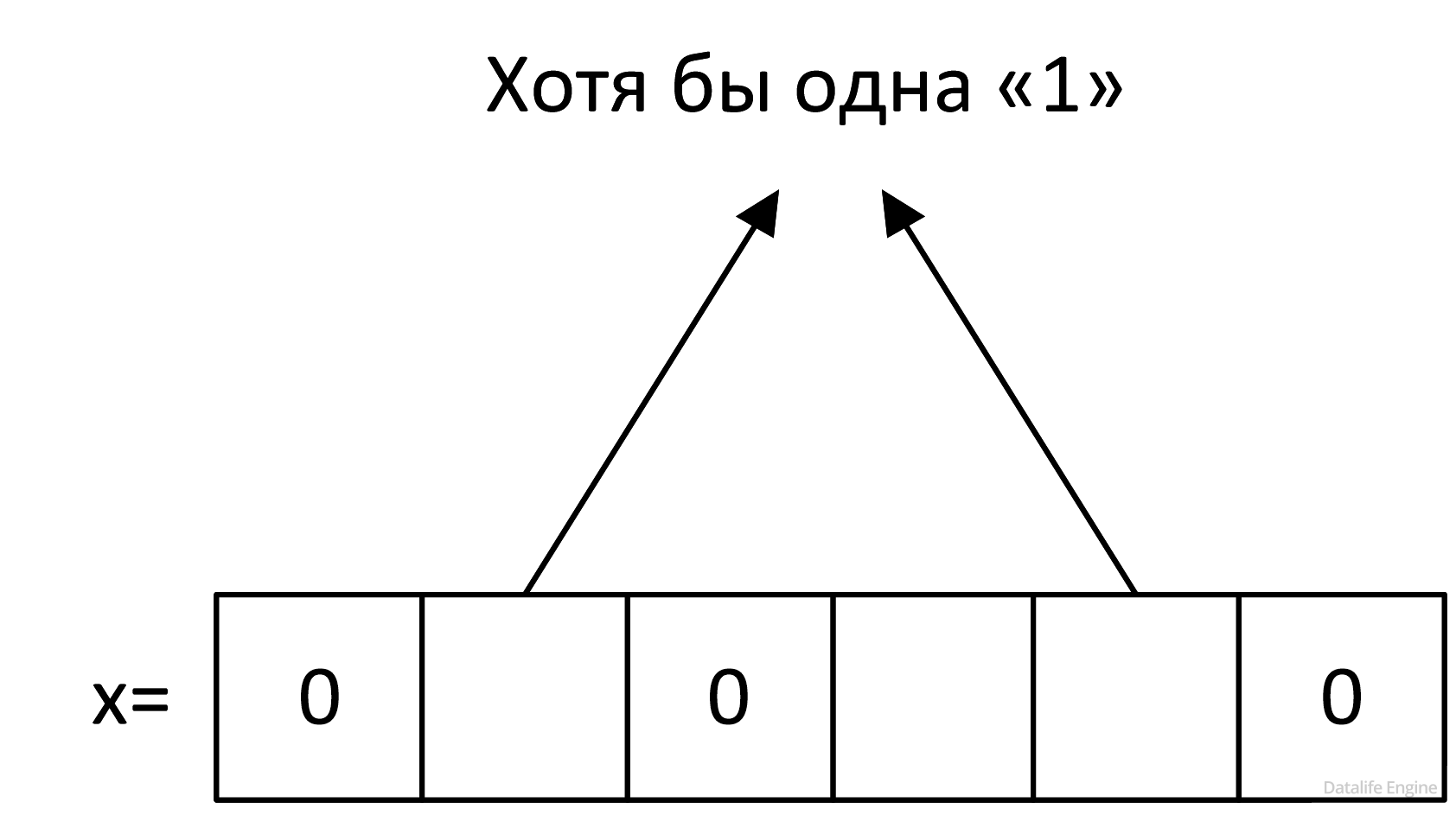
Рассмотрим третье «слагаемое»:
x & ????? = 0
Чтобы оно было ложным в большинстве случаев, мы должны заполнить его, по возможности, единичками. У нас есть один бит – четвертый, если считать слева направо, о котором мы еще ничего не можем сказать по результатам проведенного исследования. Заполним его единичкой:
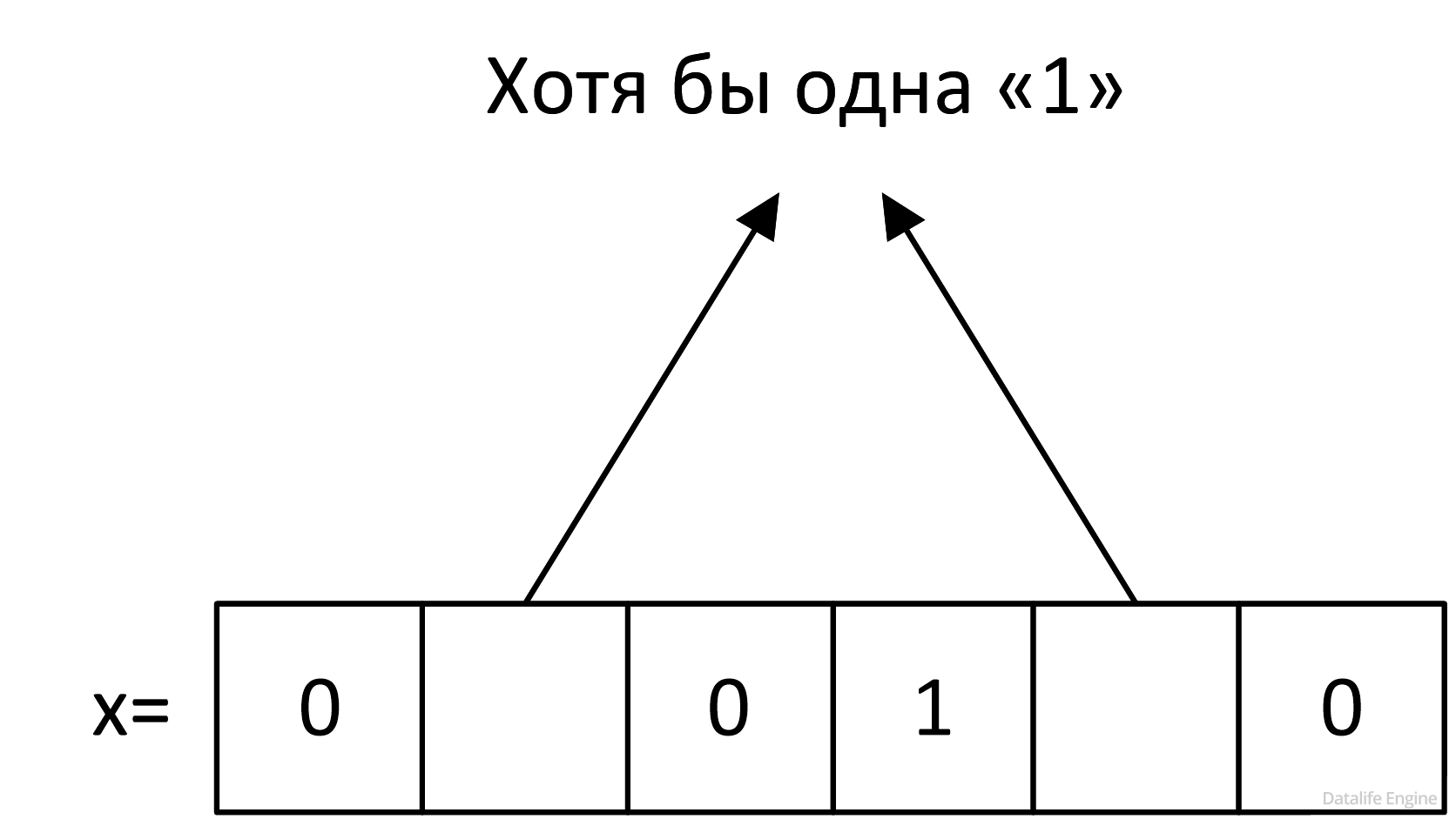
Сформируем теперь шаблон для А. Так как мы ищем x & ????? = 0, мы должны обнулить все единички во «вредном» х. На местах нулей «вредного» х мы можем поставить что угодно:
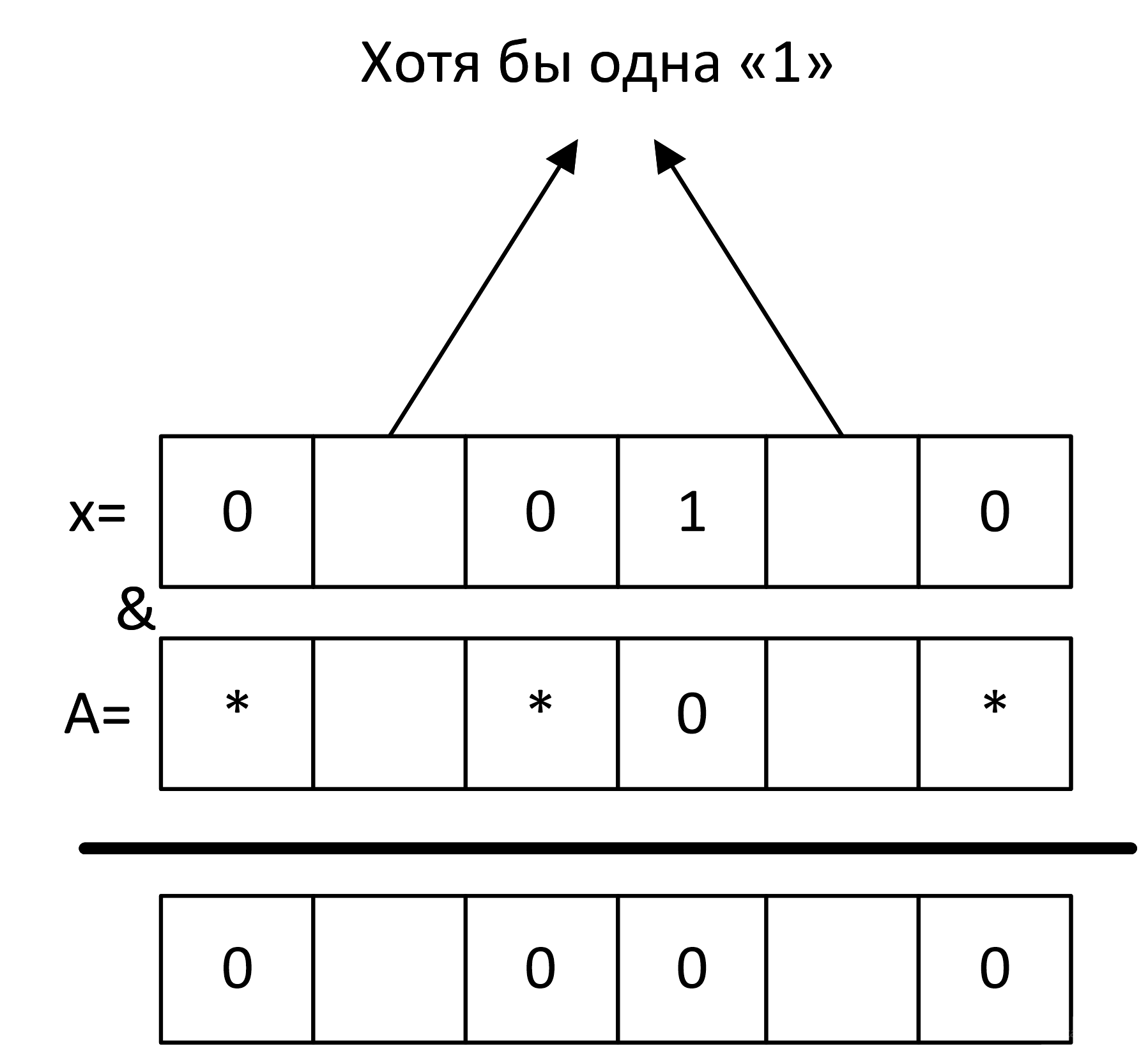
Итак, мы сделали часть шаблона для А:
А = *?*0?*
Осталось заполнить два бита. В соответствии с картинкой, таких «вредных» х три:
000110, 010100, 010110. Так как при поразрядной конъюнкции мы должны получить одни нули, берем самый трудный вариант: 010110
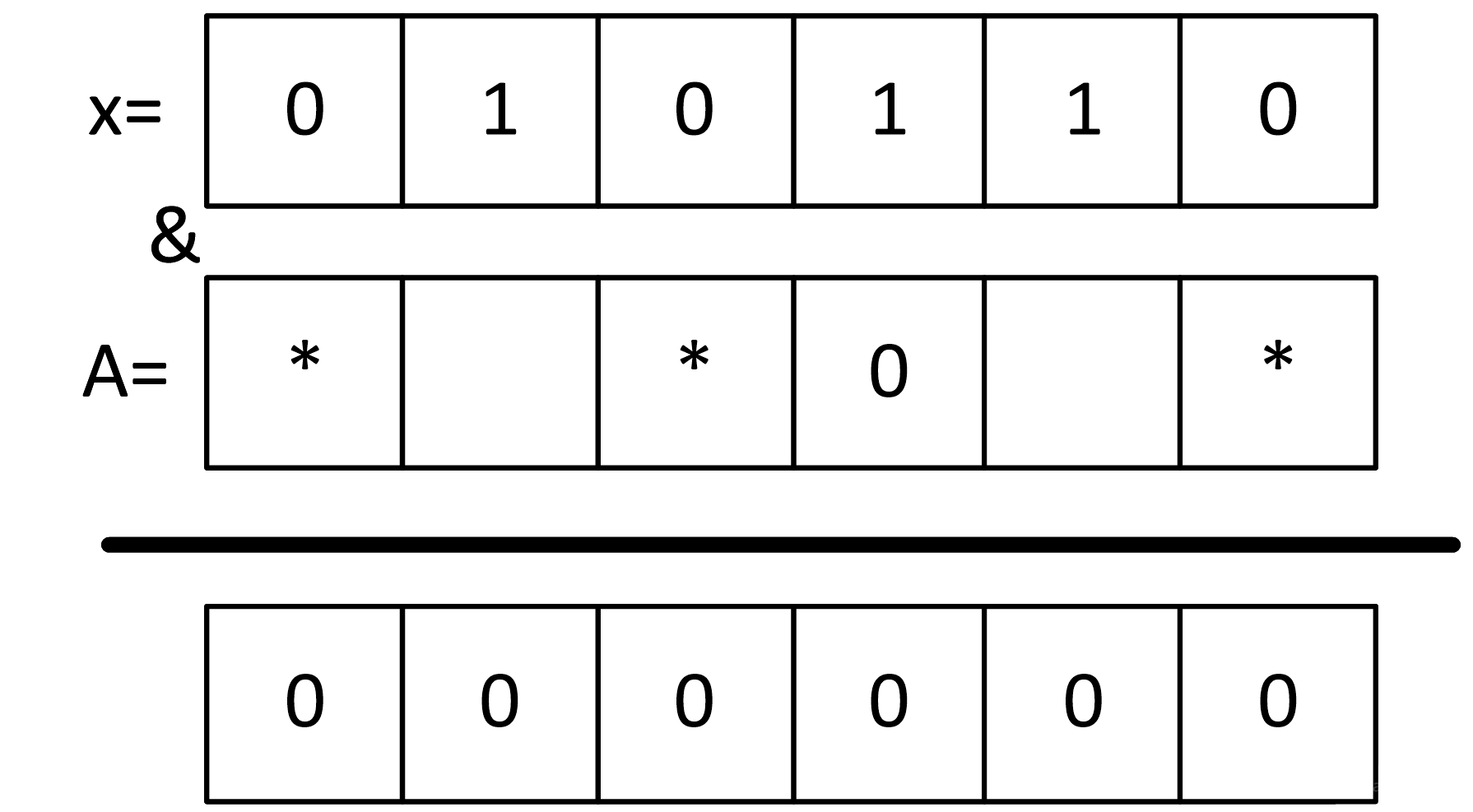
Заполняем недостающие биты в А нулями:
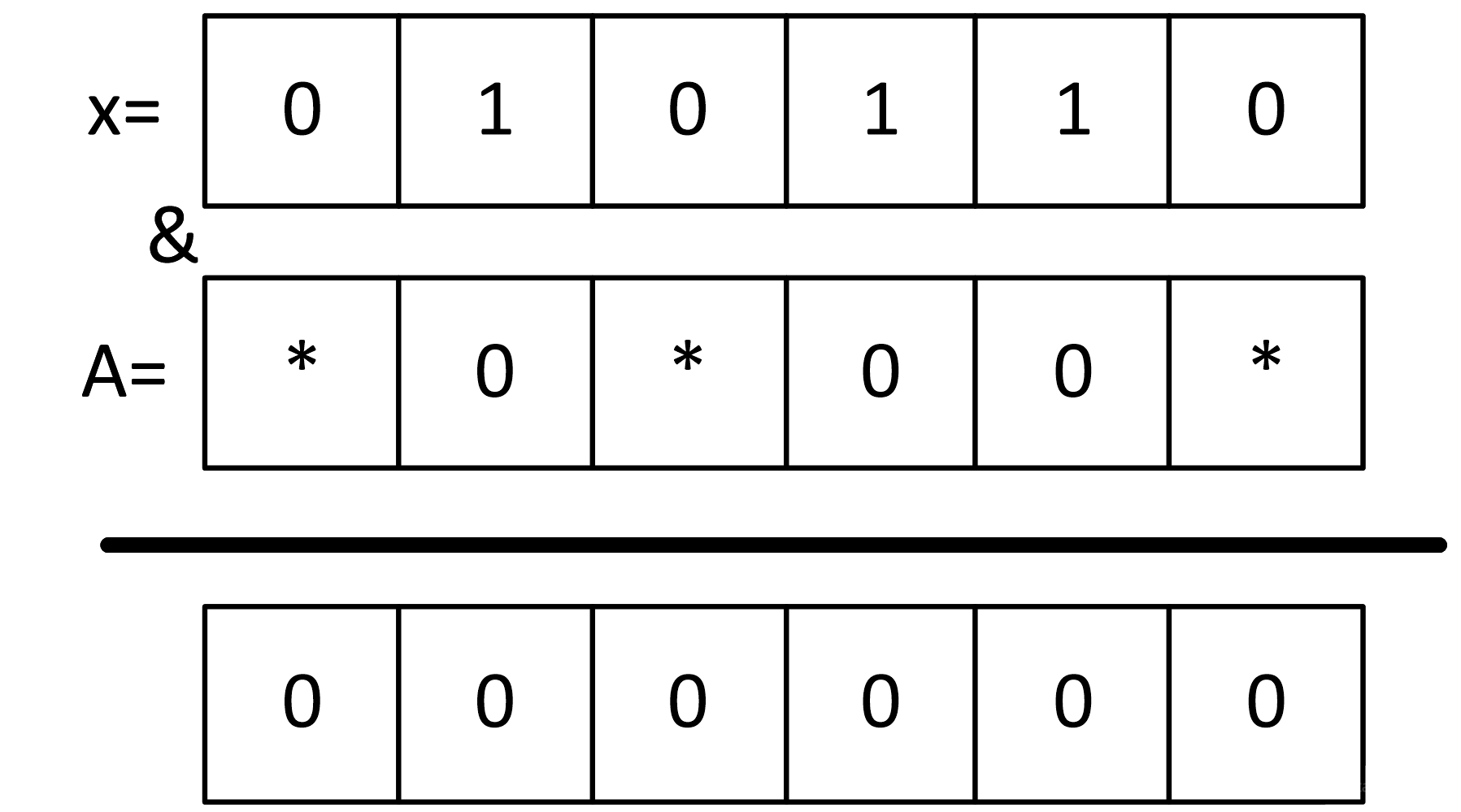
Итак, мы получили шаблон для А:
А = *0*00*
Если мы сравним его с шаблоном, полученным в дополнительных действиях (А = *0**0*), то мы увидим, что вновь полученный шаблон более точен.
Так как мы ищем максимальное А, заполним звездочки единичками:
А = *0*00* = 101001 = 41.
Ответ: 21.
Решим еще одну задачу, чтобы обратить внимание на ряд нюансов.
Задача 4.2.9.
Для какого наименьшего неотрицательного целого числа А формула
((x & 28 ≠ 0) ∨ (x & 41 ≠ 0)) → ((x & 17 = 0) → (x & А ≠ 0))
тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?
Преобразуем выражение в более удобное для анализа.
Заменим «следования» на логические «или»:
⌐((x & 28 ≠ 0) ∨ (x & 41 ≠ 0)) ∨ ((x & 17 ≠ 0) ∨ (x & А ≠ 0))
По закону де Моргана раскроем скобки у общего отрицания в первом «слагаемом»:
((x & 28 = 0) ∧ (x & 41 = 0)) ∨ (x & 17 ≠ 0) ∨ (x & А ≠ 0)
Переведем числа из десятичной в двоичную систему:
((x & 11100 = 0) ∧ (x & 101101 = 0)) ∨ ((x & 10001 ≠ 0) ∨ (x & А ≠ 0))
Максимальное количество битов – шесть, дополним незначащими нулями:
((x & 011100 = 0) ∧ (x & 101101 = 0)) ∨ ((x & 010001 ≠ 0) ∨ (x & ?????? ≠ 0))
Как и в предыдущих задачах, начнем подбирать наиболее проблемный x, при котором большинство частей выражения будет ложно.
Рассмотрим первое выражение:
x & 011100 = 0
Чтобы оно было ложным, достаточно, чтобы на месте 1 выражения 011100 в соответствующих позициях х стояла хотя бы одна 1:
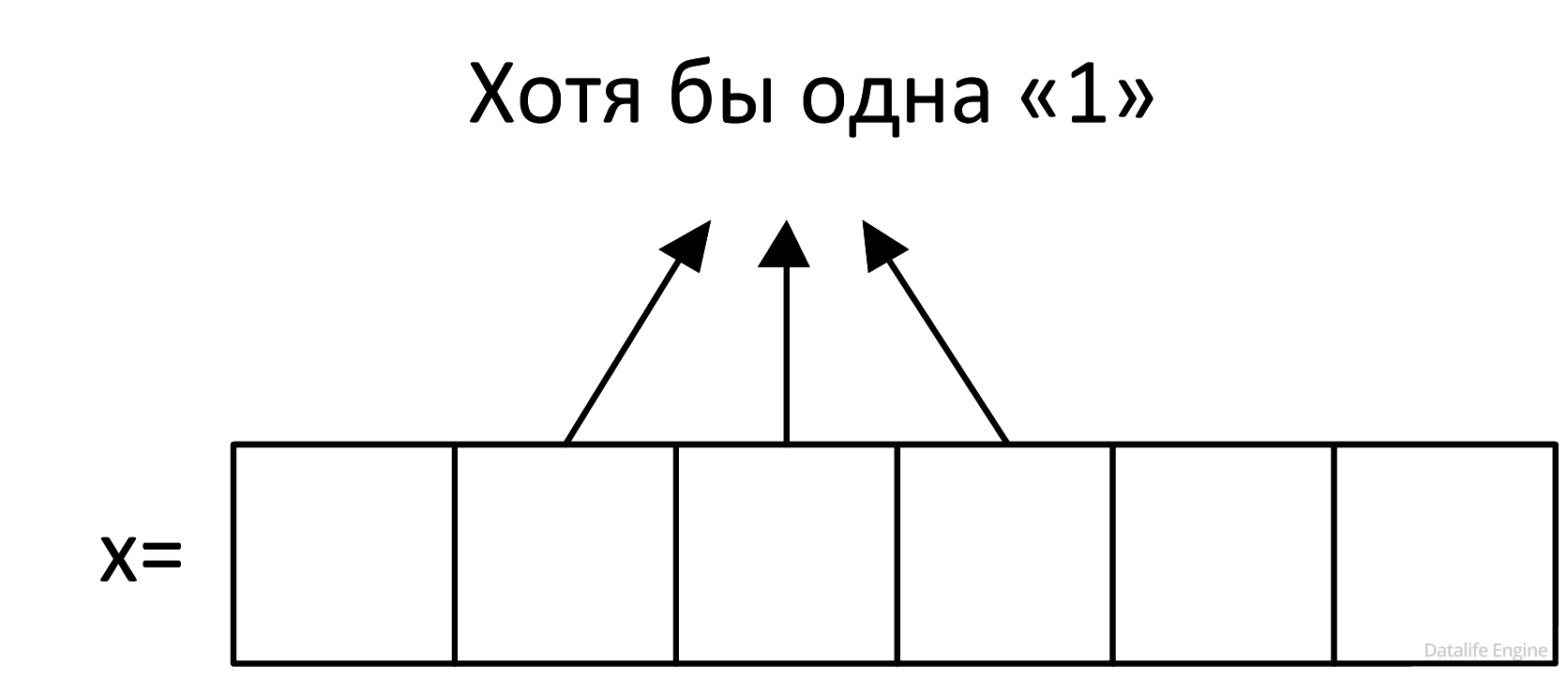
Рассмотрим второе выражение:
x & 101101 = 0
Аналогично первому выражению, для второго получаем:

Можем ли мы объединить эти два условия наличия единиц?
Или при выполнении только верхнего условия:

нам потребуется обязательно заполнить единицами первый и/или последний бит?
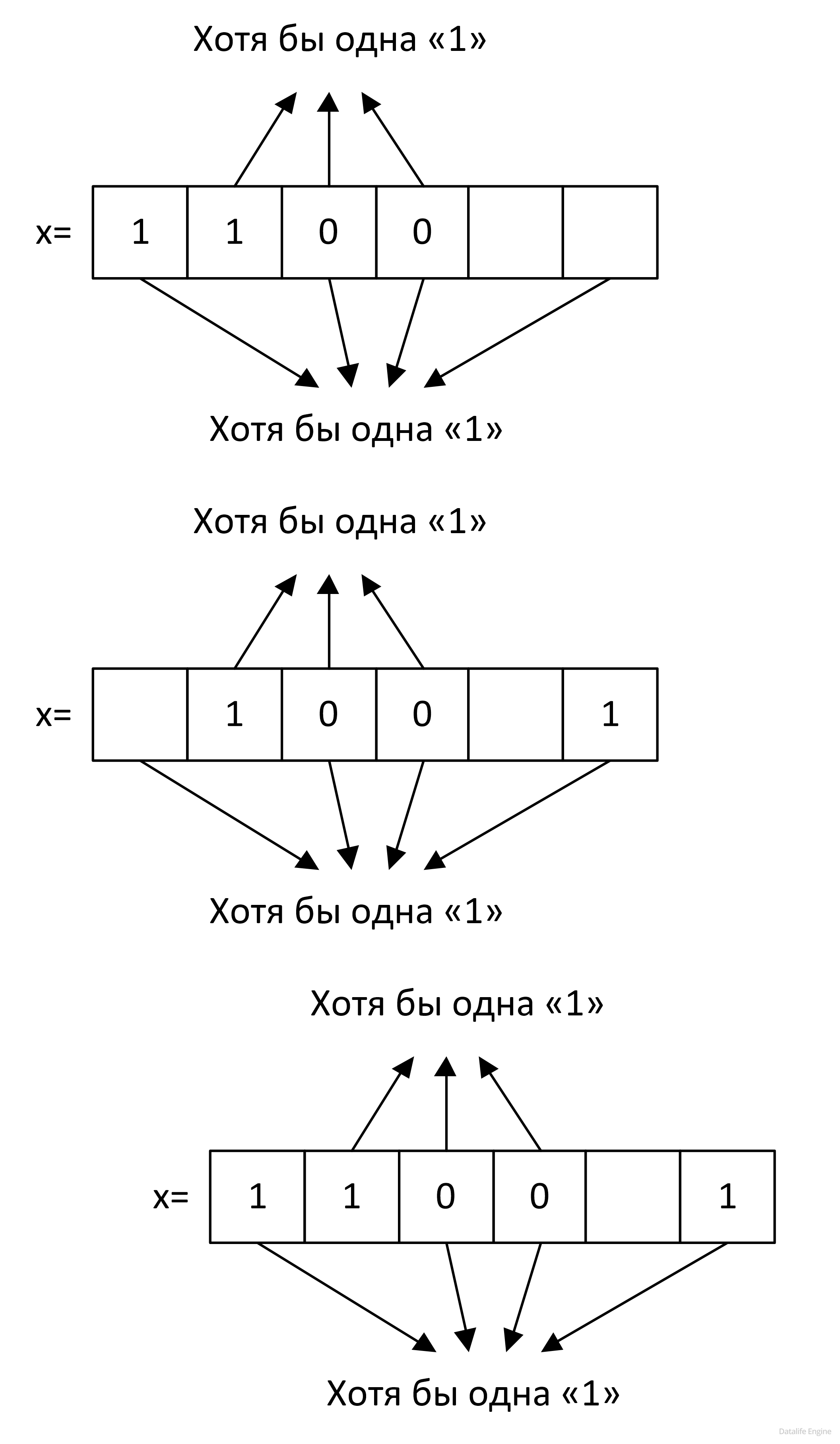
Обратим внимание на связку между первым и вторым выражением:
((x & 28 = 0) ∧ (x & 41 = 0))
Они связаны логическим «и», следовательно, чтобы итоговое выражение было ложным, нам достаточно нарушения хотя бы одного из входящих выражений. Следовательно, мы вполне можем сделать такую трансформацию:
|

|
=>
|

|
Заметим, что, если бы была связка с помощью логического «или», такая трансформация была бы невозможной.
Рассмотрим третье выражение:
x & 010001 ≠ 0
Чтобы оно было ложным, надо, чтобы на тех местах, где в 10001 идут единицы, в x были нули:
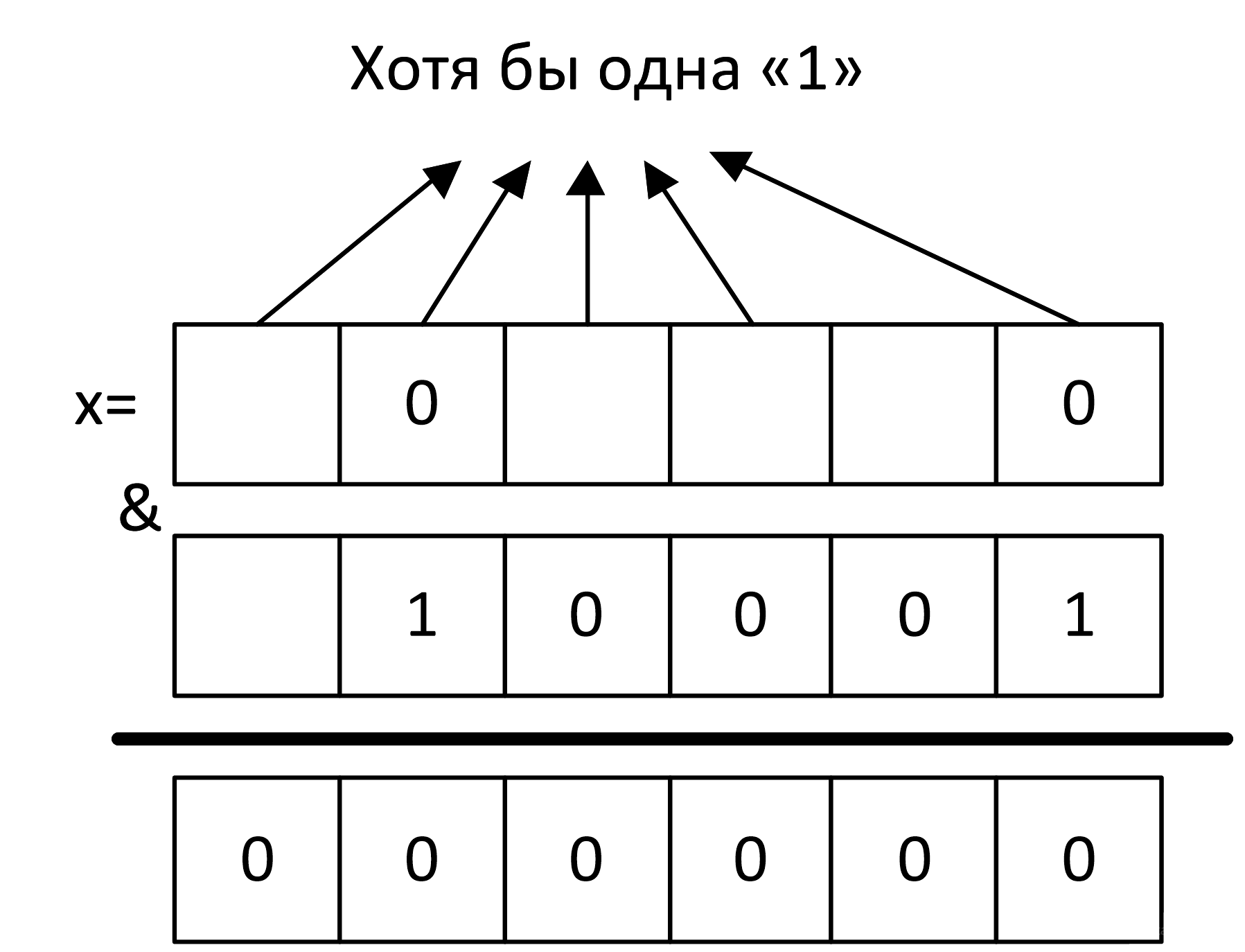
Избавляемся от лишних стрелочек:
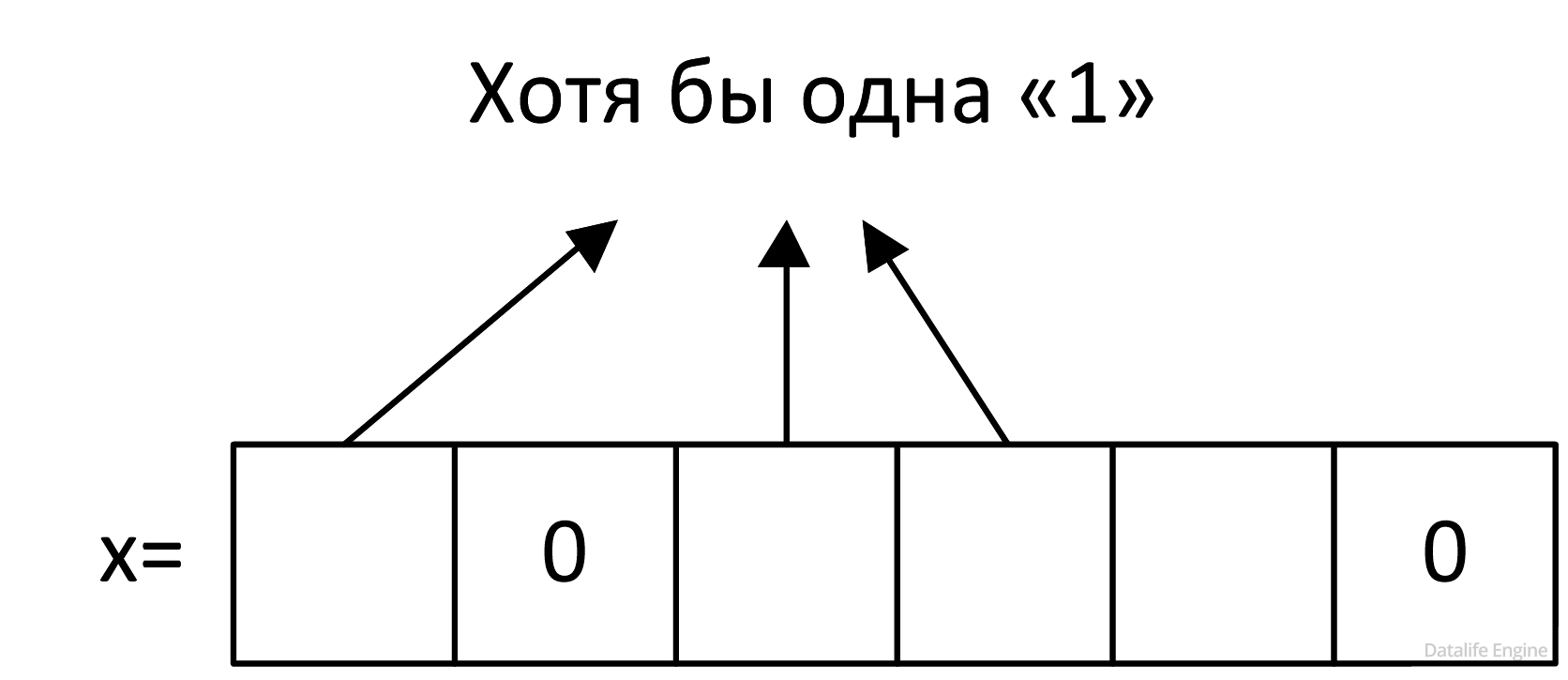
Рассмотрим четвертое выражение:
x & ?????? ≠ 0
Чтобы оно было ложным, нужно, чтобы было как можно больше нулей в «проблемном» х. Заполним оставшийся неизвестным бит в х нулем:
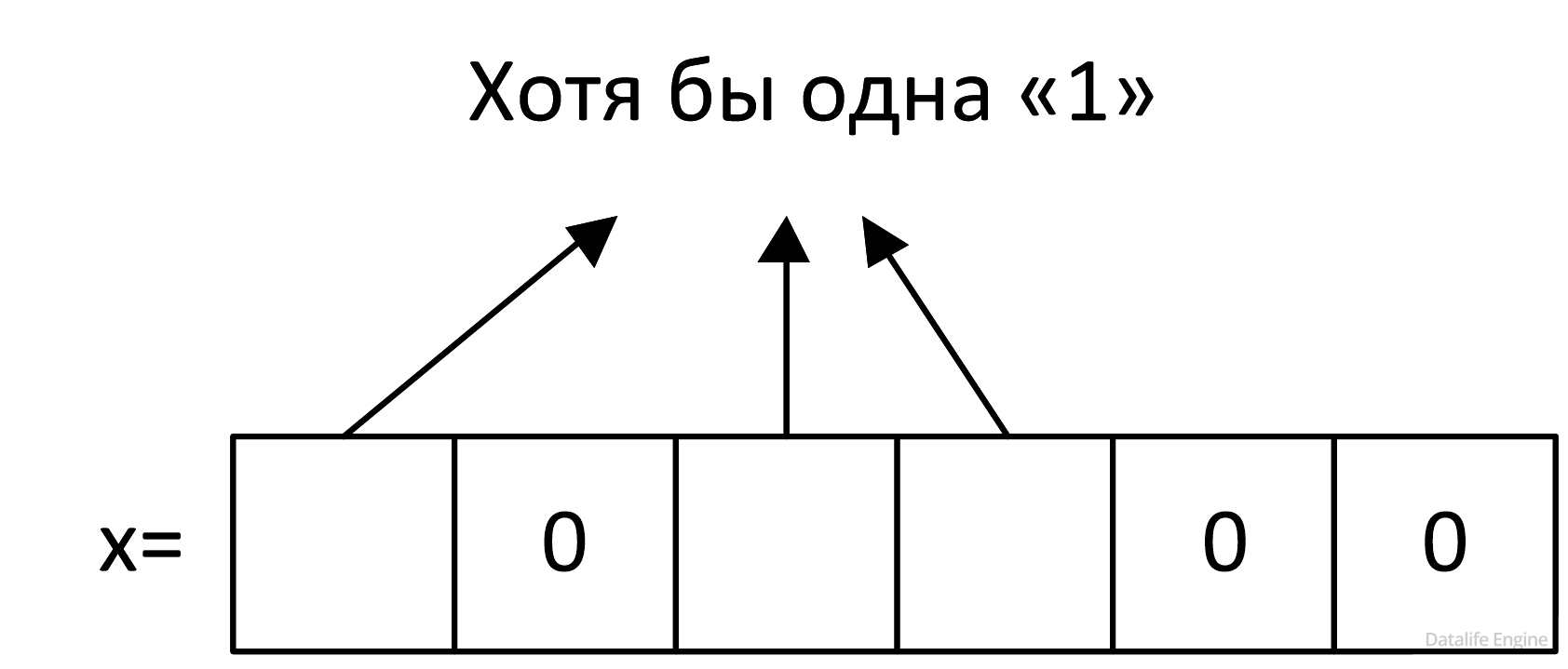
При найденном шаблоне x (на рисунке выше) все выражения, в которых числа известны, ложны, следовательно,
x & ?????? ≠ 0
должно быть истинным.
Начнем формировать шаблон для А:
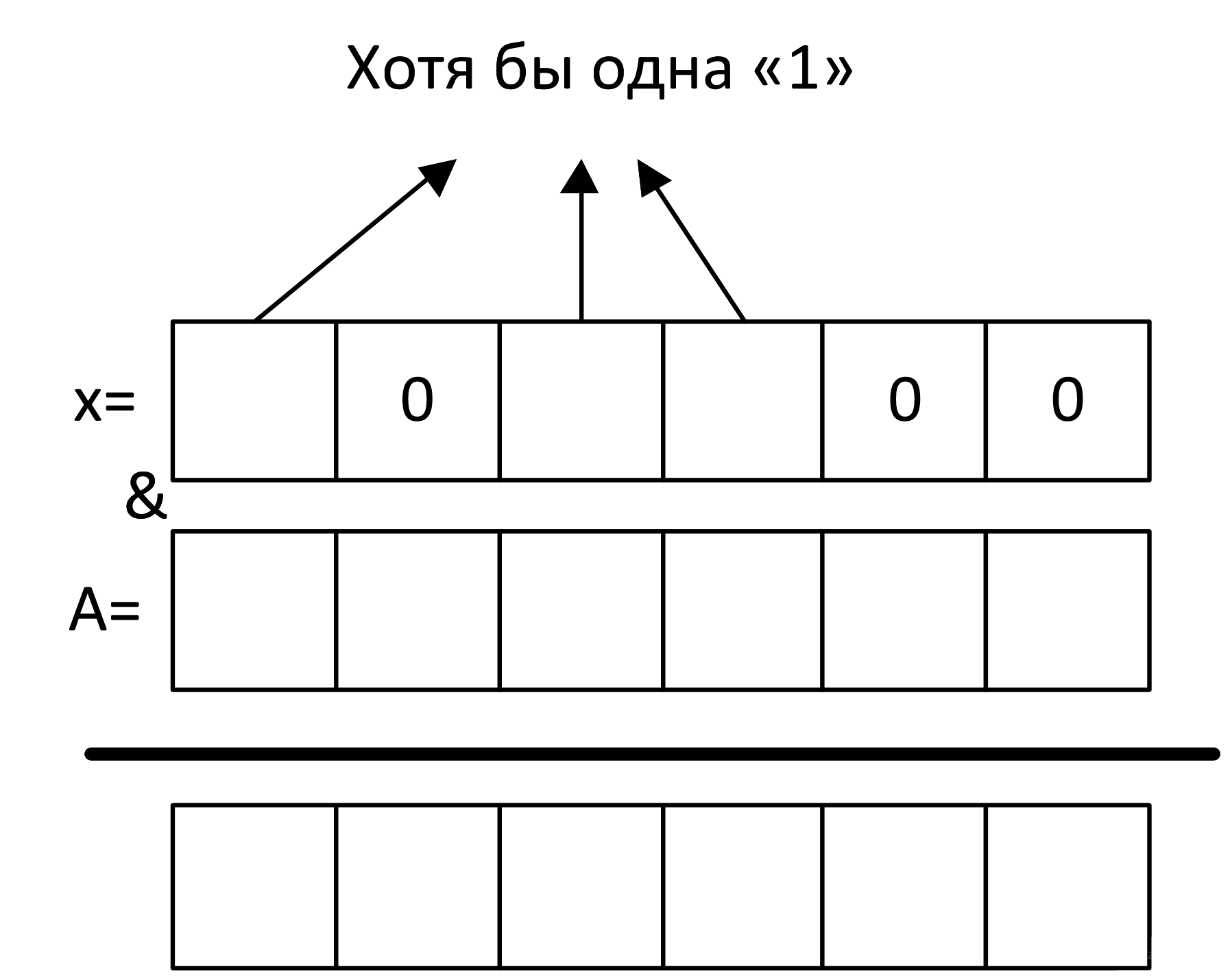
Чтобы выражение не было равным нулю, надо, чтобы хотя бы 1 бит в результате был неравным нулю:

Там, где идут нули в проблемном x, в результате получится 0 независимо от того, что идет в А:

Избавляемся от лишних стрелочек:
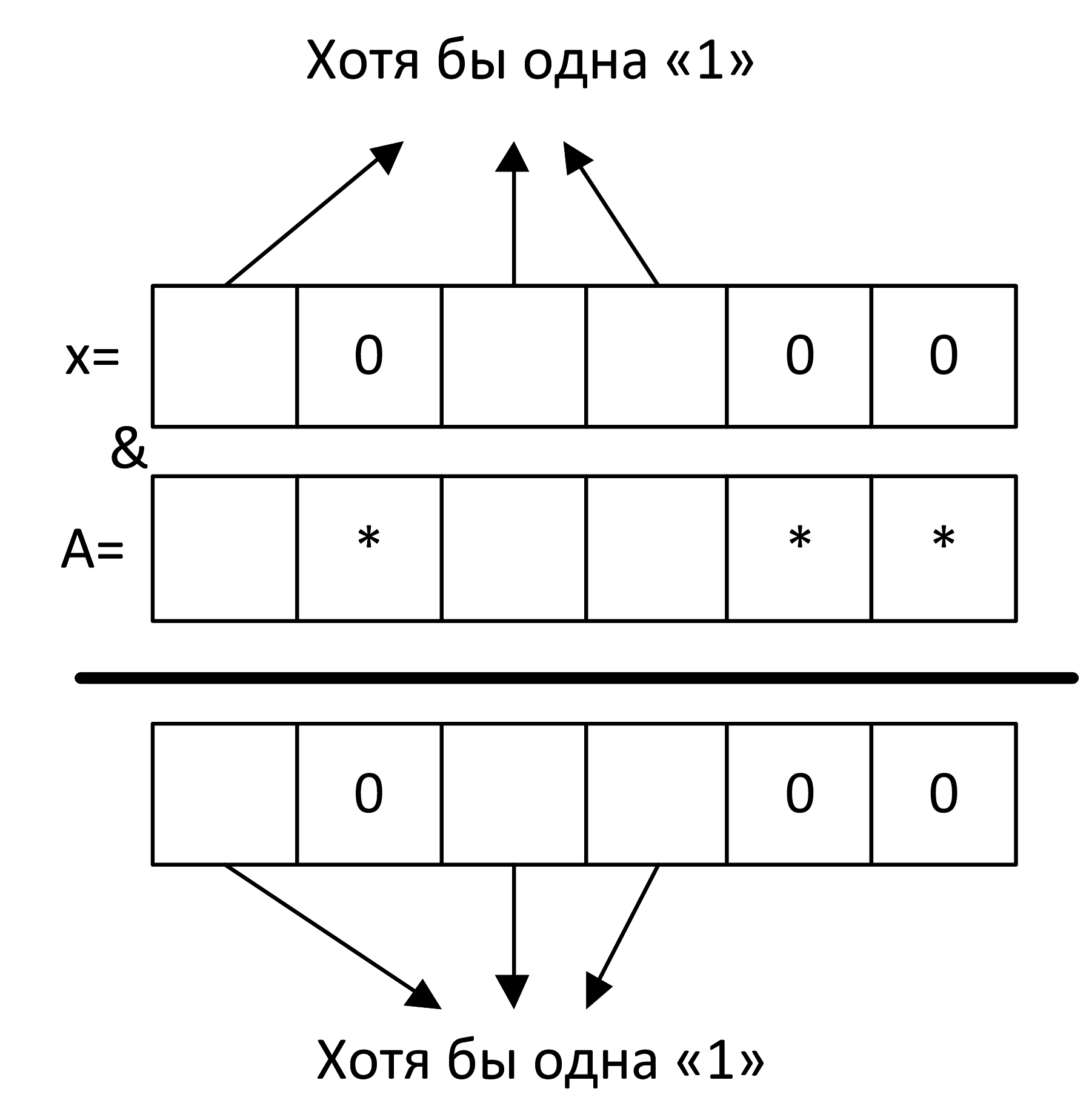
Поскольку мы не знаем, в каком из битов проблемного x идут единицы, а в каком – нули, если мы хотим, чтобы в результате была хотя бы одна единица, нам нужно, чтобы в А на месте пропусков были все единицы:
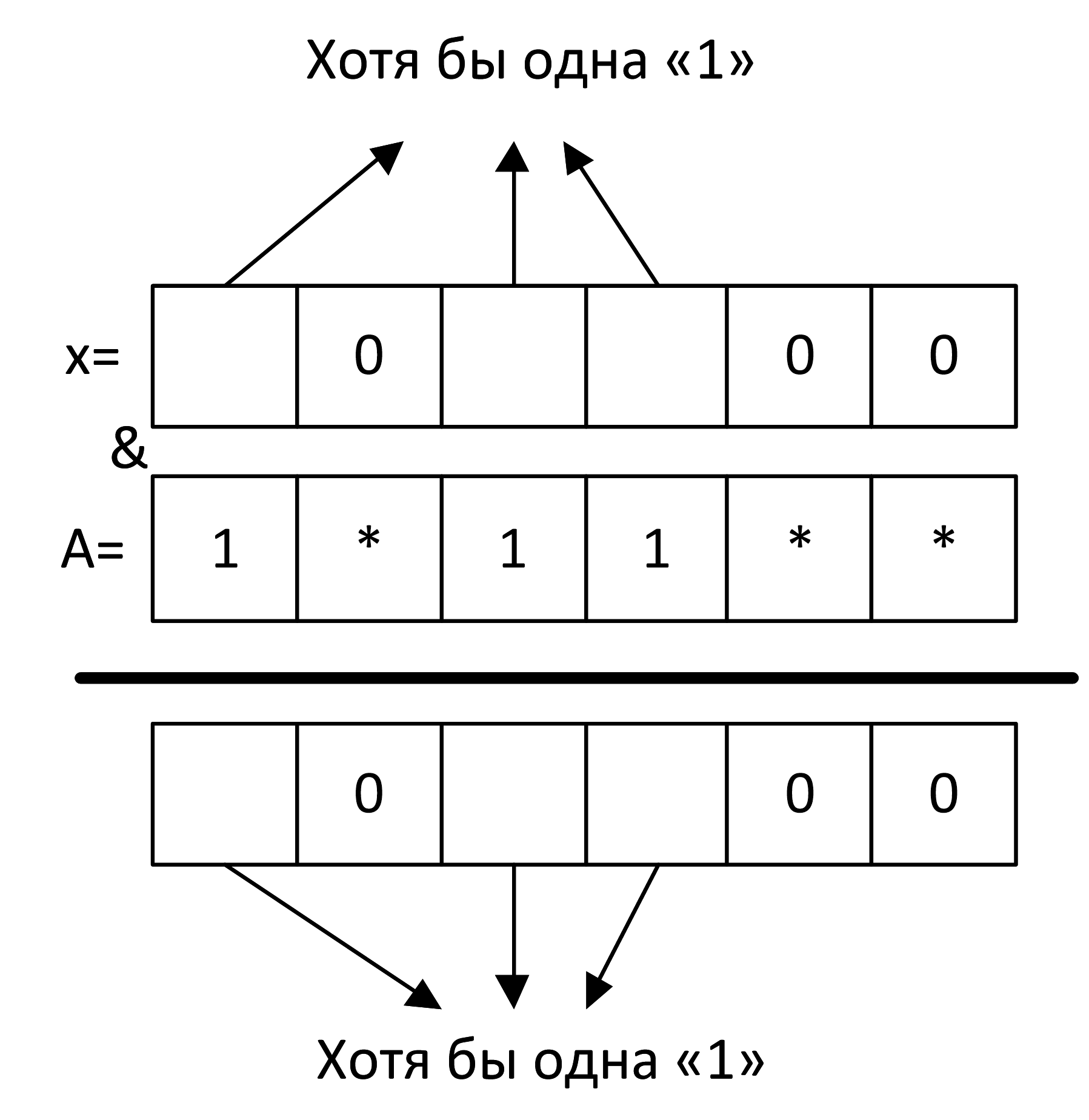
Таким образом, мы имеем шаблон для А = *111**. Так как мы ищем наименьшее А, то:
А = 1*11** = 101100 = 44
Ответ: 44
Примечание: С поразрядной конъюнкцией мы еще встретимся в параграфе об IP-адресации. Эта тема объединяет системы счисления, логику и комбинаторику.