Продолжим решать задачи на круги Эйлера.
Задача 4.3.1. Ниже приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
Воспользуйтесь кругами Эйлера.
Для каждого высказывания построим круги Эйлера (размер кругов сделаем условно одинаковым, так как мы не знаем количество найденных страниц):
- принтеры & сканеры & продажа – те страницы, которые одновременно содержат все три слова
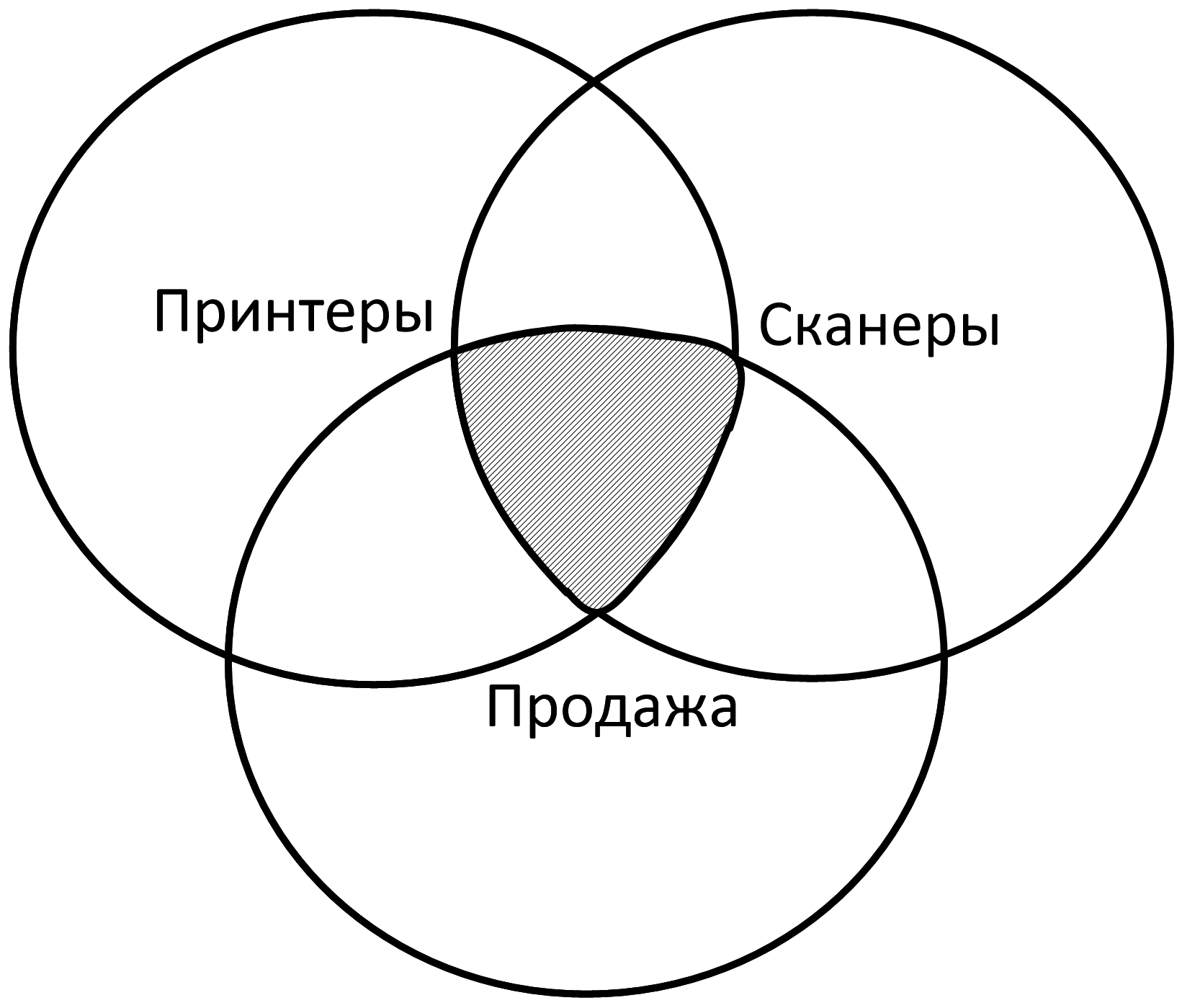
|
2) принтеры & продажа – страницы, которые одновременно содержат оба слова

|
|
3) принтеры | продажа – страницы, которые содержат хотя бы одно из двух слов
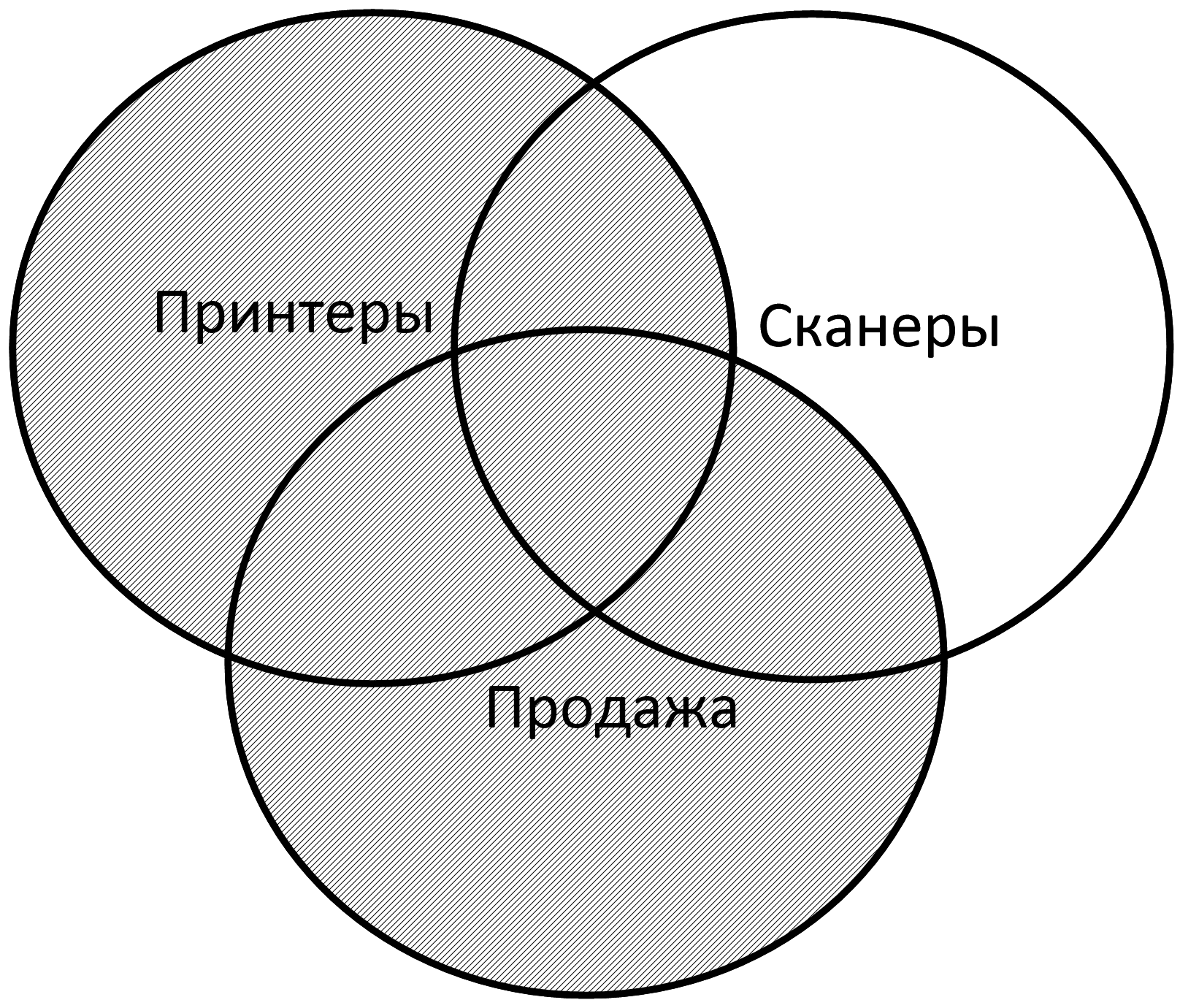
|
4) принтеры | сканеры | продажа– страницы, которые содержат хотя бы одно из трех слов
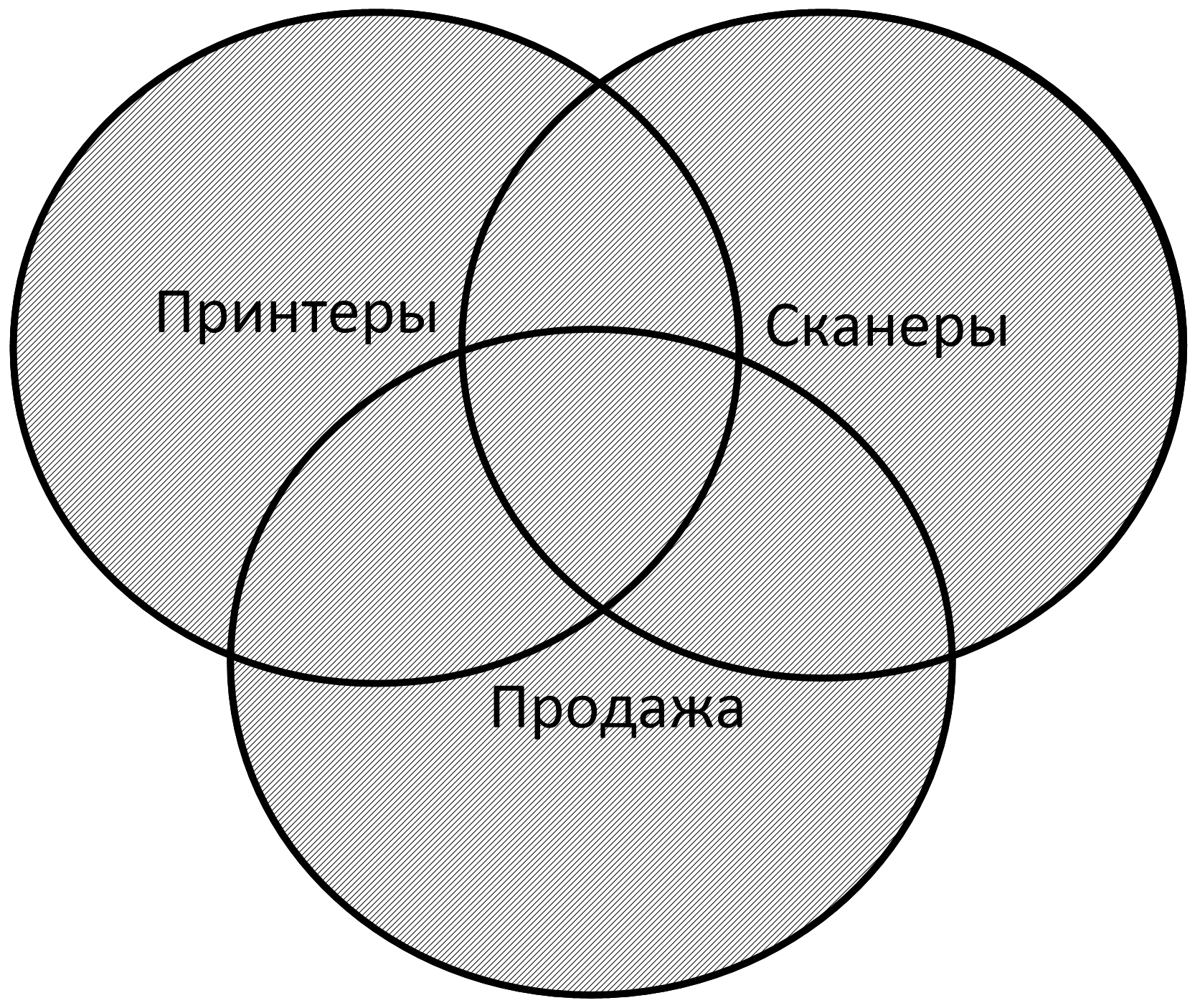
|
Ответ: 1234
Задача 4.3.2. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос
|
Найдено страниц
(в тысячах)
|
|
Спартак
|
45000
|
|
Красс
|
2000
|
|
Динамо
|
49000
|
|
Спартак & Красс
|
1700
|
|
Спартак & Динамо
|
36000
|
По запросу Динамо & Красс ни одной страницы найдено не было.
Какое количество страниц (в тысячах) будет найдено по запросу Спартак | Динамо | Красс?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нарисуйте круги Эйлера и начинайте заполнять их сегменты количеством страниц, начиная с запросов с наименьшим количеством страниц.
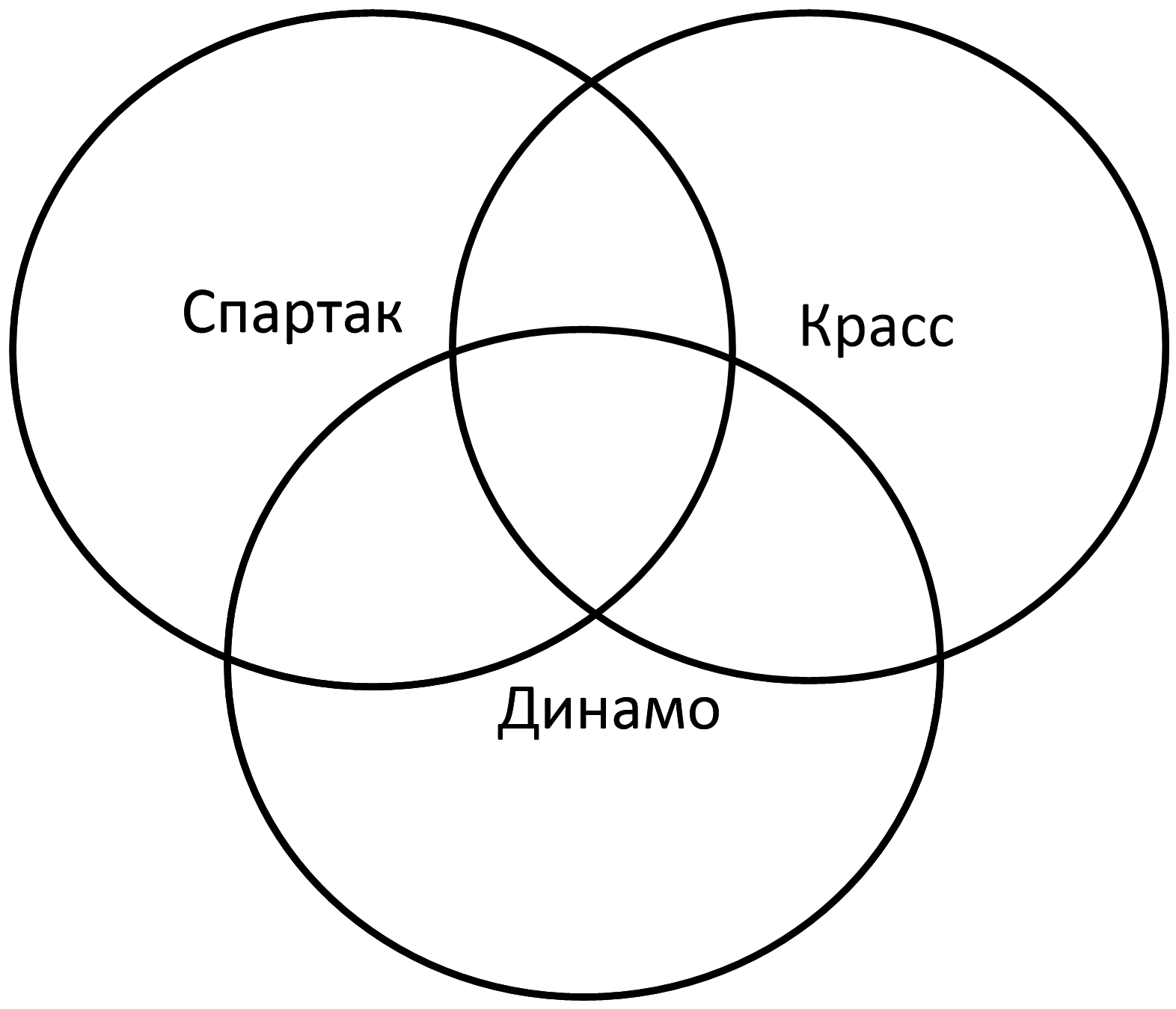
По запросу Динамо & Красс ни одной страницы найдено не было. Ставим нули в два сегмента пересечения кругов Динамо и Красса:

Спартак & Красс = 1700:
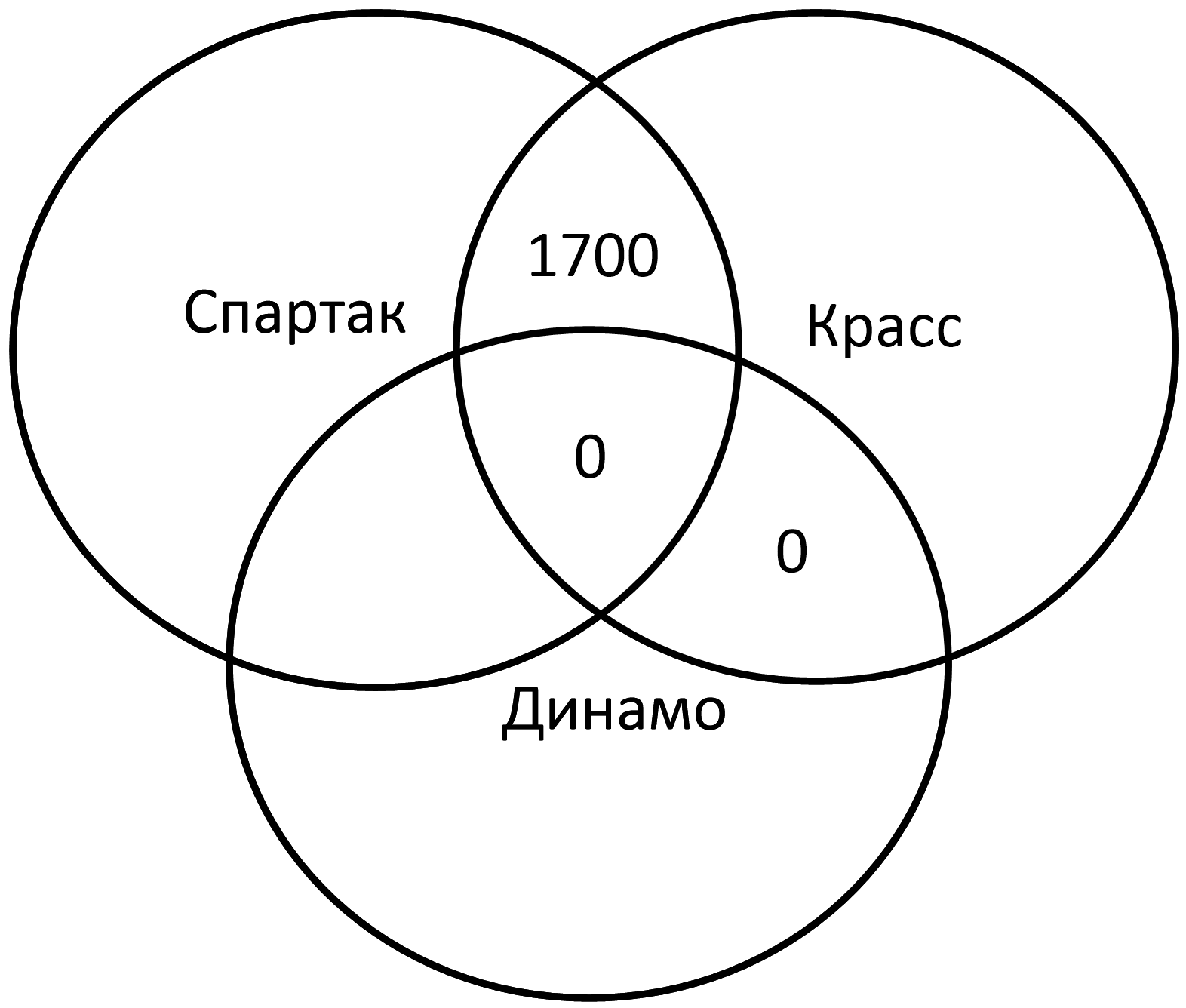
Спартак & Динамо = 36000
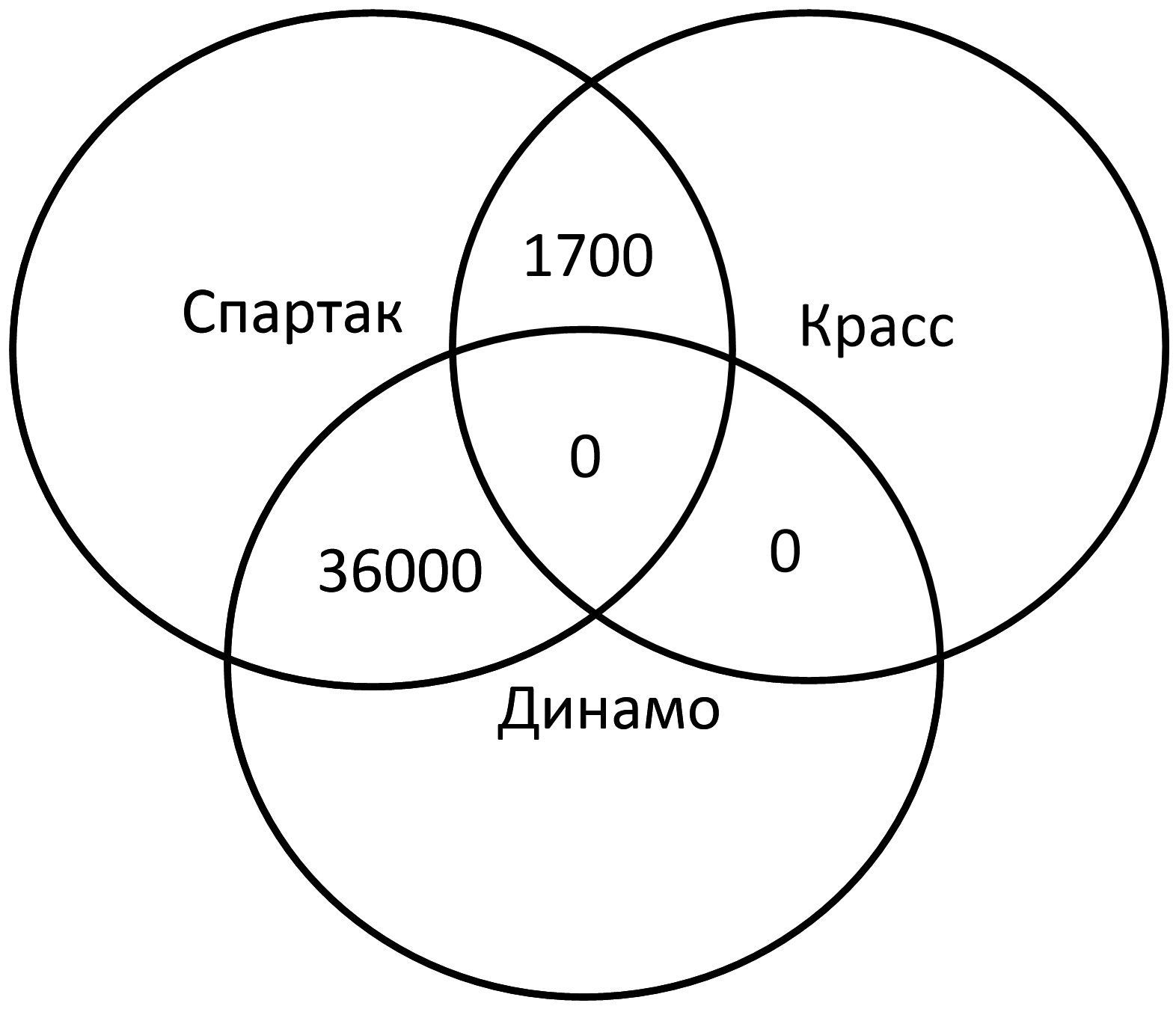
Только Спартак = 45000 – 36000 – 1700 = 7300
Только Красс = 2000 – 1700 = 300
Только Динамо = 49000 – 36000 = 13000
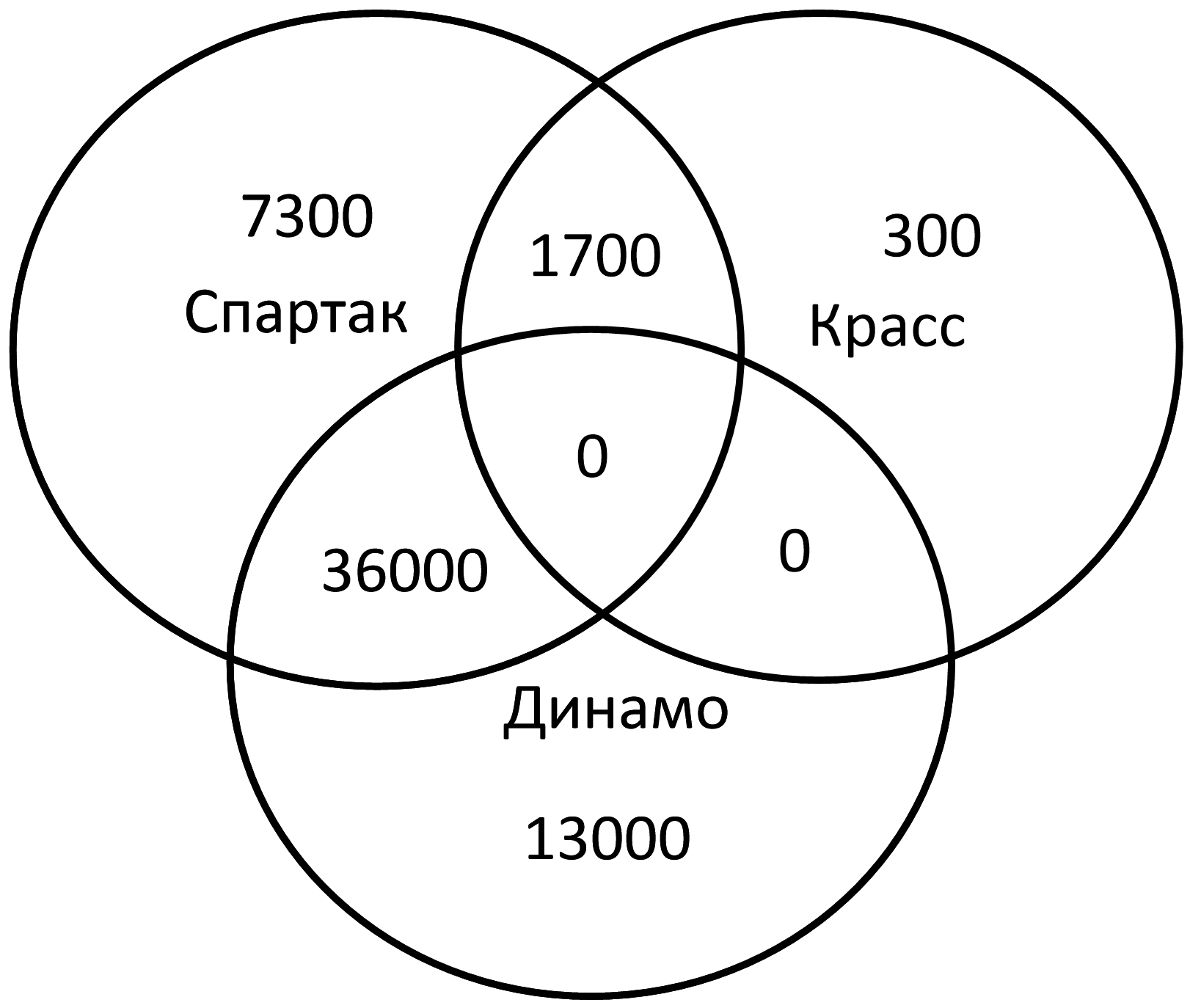
Мы посчитали количество страниц во всех сегментах.
Спартак | Динамо | Красс – это все сегменты одновременно:
7300 + 1700 + 300 + 36000 + 13000 = 58300
Ответ: 58300
Задача 4.3.3. В таблице приведены запросы и количество найденных по ним страниц в Интернете:
|
Запрос
|
Найдено страниц (в сотнях тысяч)
|
|
Ухо
|
35
|
|
Подкова
|
25
|
|
Наковальня
|
40
|
|
Ухо | Подкова | Наковальня
|
70
|
|
Ухо & Наковальня
|
10
|
|
Ухо & Подкова
|
0
|
Какое количество страниц (в сотнях тысяч) будет найдено по запросу Подкова & Наковальня?
Нарисуйте круги Эйлера и начните их заполнять. Не всегда получается заполнить все сегменты числами «с ходу». В этой задаче некоторые сегменты придется обозначить буквами и решить систему уравнений.
Построим круги Эйлера:
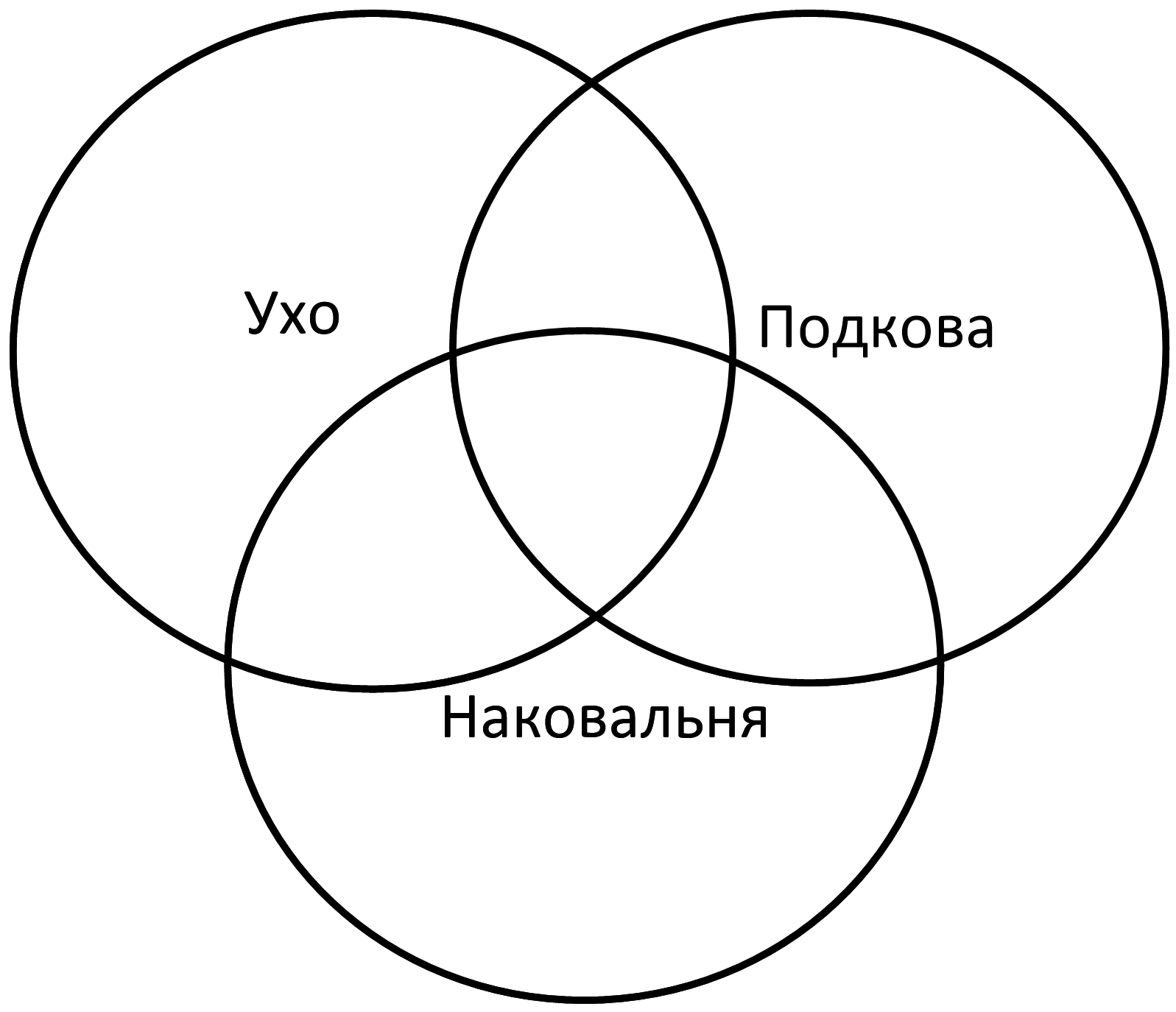
Так как Ухо & Подкова = 0:

Ухо & Наковальня = 10, Только Ухо = 35 – 10 = 25

Дальше проставить числа в секторы без системы уравнений не получится. Обозначим секторы буквами:
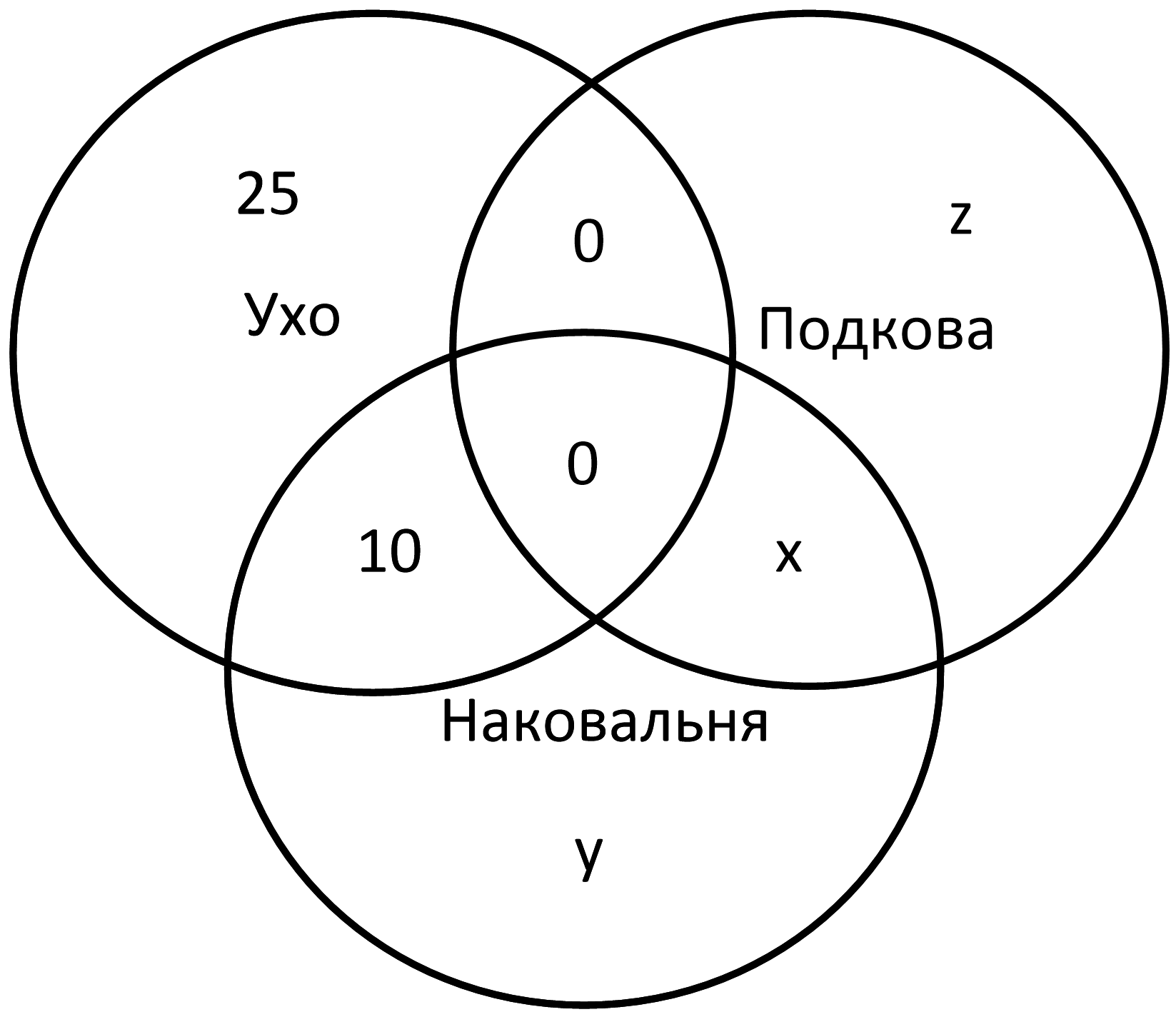
Используем еще не применявшиеся данные из задания:
x + y = 40 – 10
x + z = 25
Сумма всех секторов:
x + y + z + 25 + 10 = 70
Получаем систему уравнений:
- x + y = 30
- x + z = 25
- x + y + z = 35
Сложим первое и второе уравнения:
2x + y + z = 30 + 25
2x + y + z = 55
Из получившегося уравнения вычтем третье:
2x + y + z – x – y – z = 55 – 35
x = 20
Ответ: 20
Задача 4.3.4. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
|
Запрос
|
Найдено страниц
(в тысячах)
|
|
Леннон & Маккартни & Старр
|
1100
|
|
Леннон & Маккартни & Харрисон
|
1300
|
|
Леннон & Маккартни & Старр & Харрисон
|
1000
|
Какое количество страниц (в тыс.) будет найдено по запросу
(Леннон & Маккартни & Старр) | (Леннон & Маккартни & Харрисон)?
Нарисуйте круги Эйлера и начните их заполнять. В этой задаче четыре круга Эйлера. Не у всех учеников получается красиво нарисовать их пересечения. Потренируйтесь
Построим круги Эйлера:
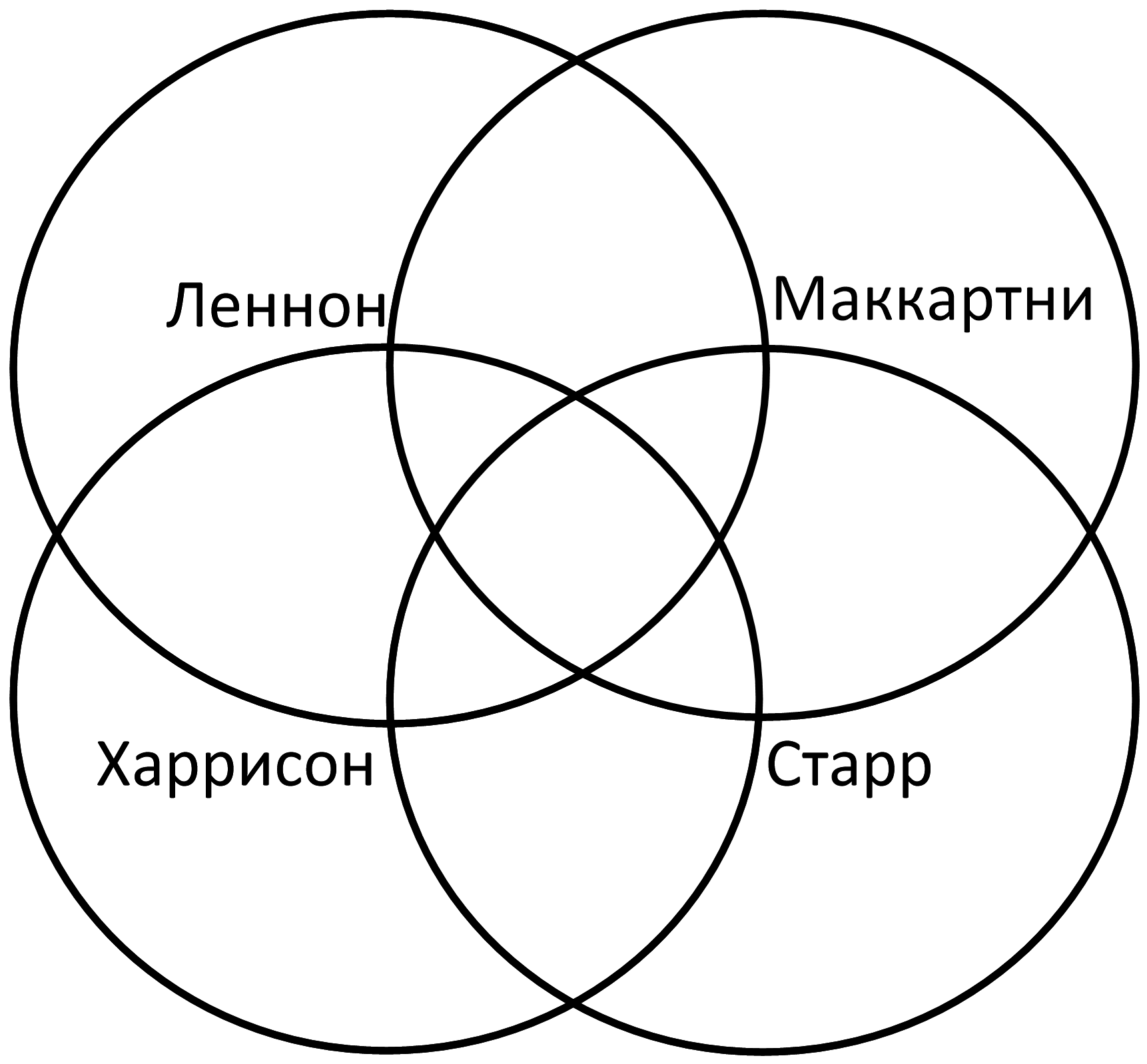
Леннон & Маккартни & Старр & Харрисон = 1000 – Это самая «сердцевина» диаграммы – область пересечения всех кругов
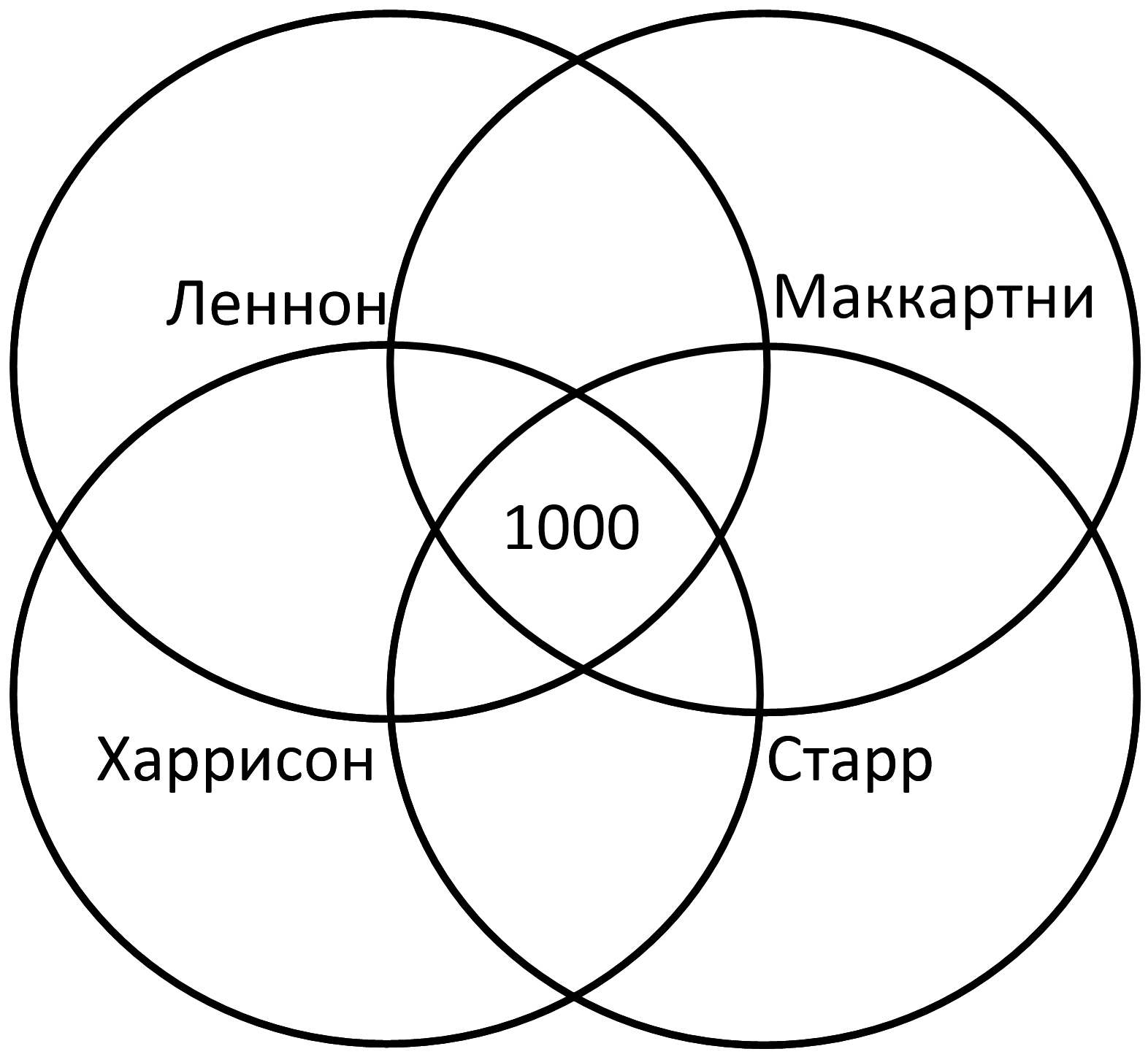
Леннон & Маккартни & Старр – 1100 – Это сегменты, общие для трех кругов, отмечены штрихом на диаграмме:
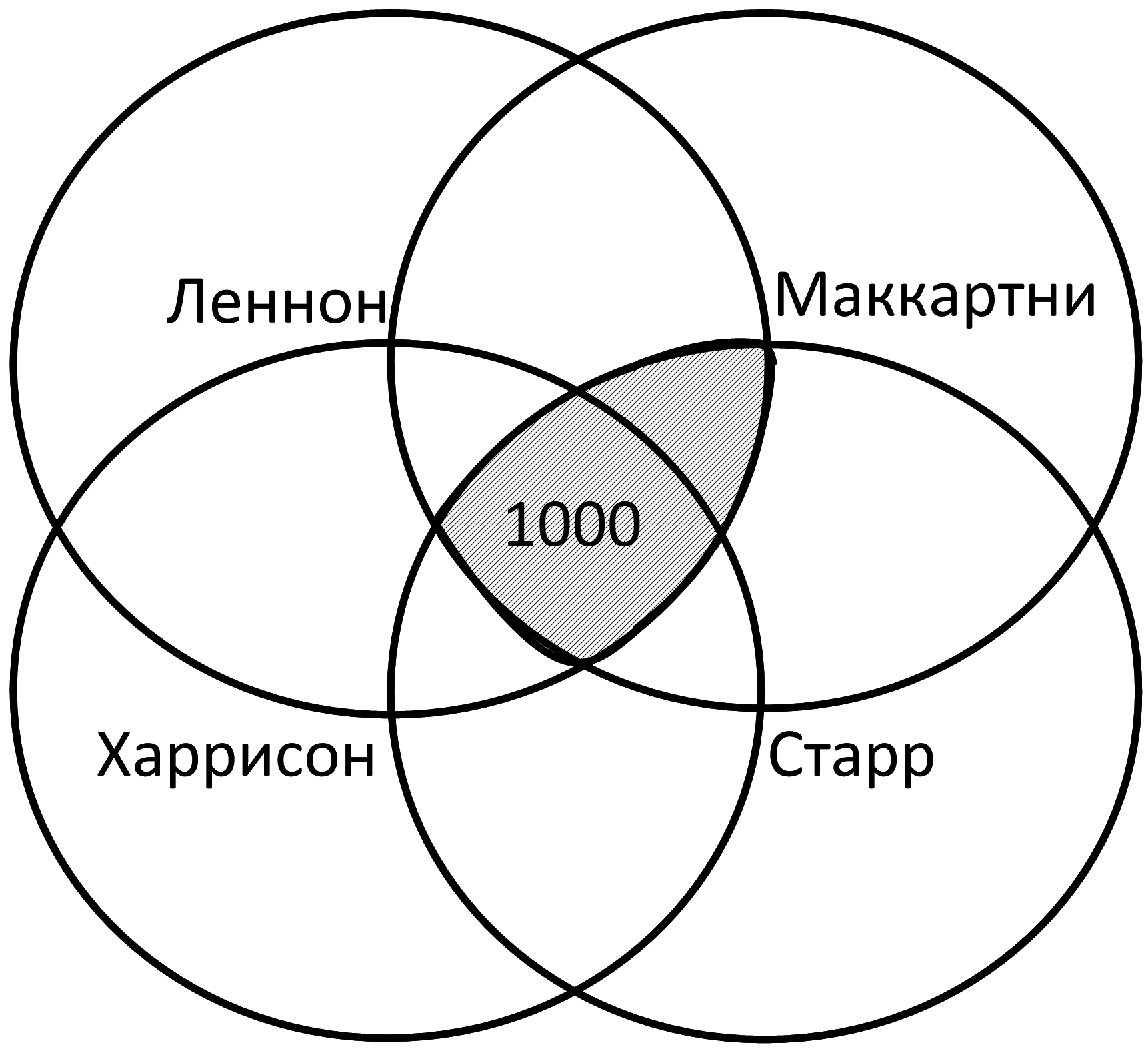
Значит, мы можем посчитать еще один сегмент: 1100-1000=100:
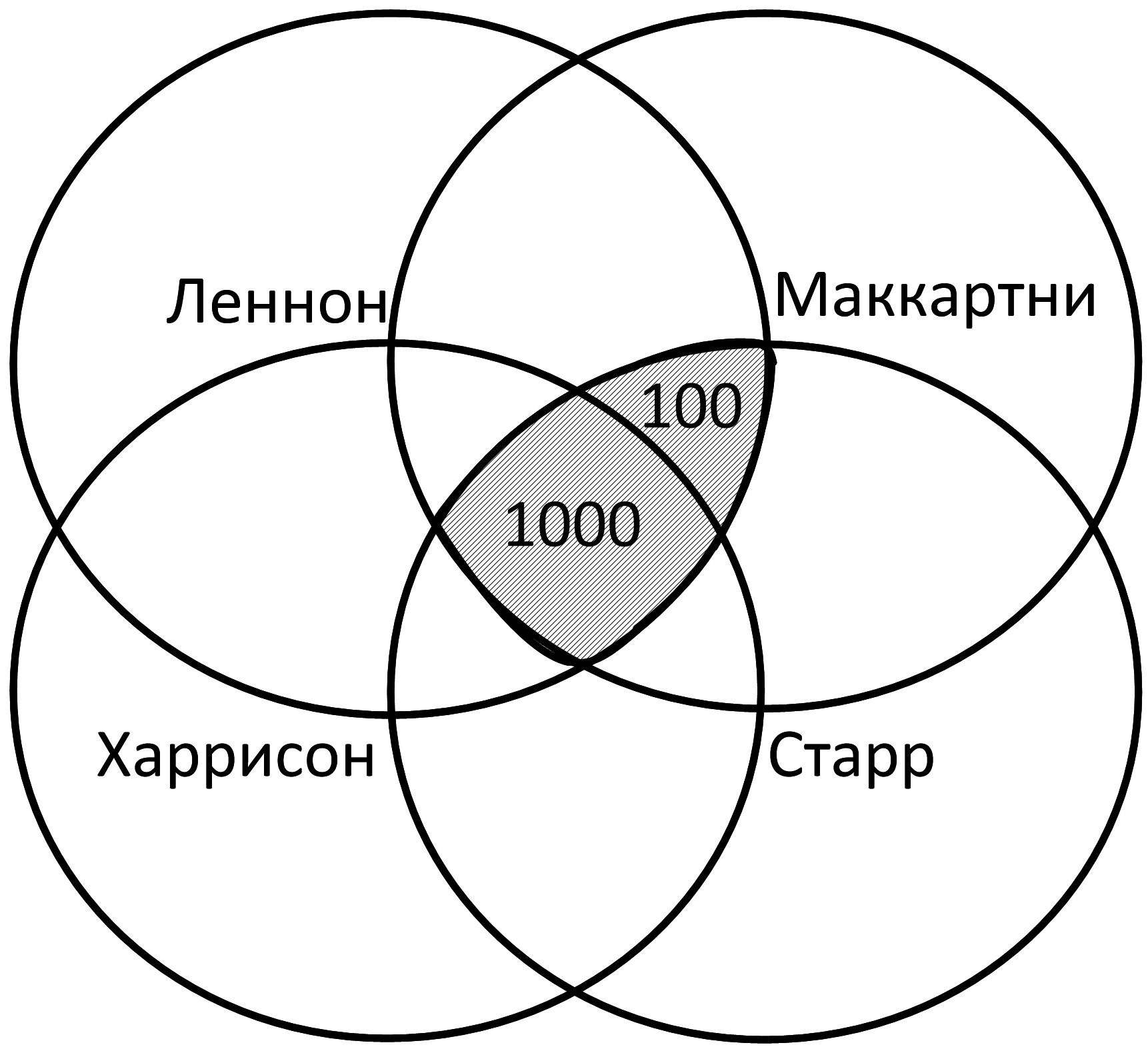
Аналогично так как Леннон & Маккартни & Харрисон = 1300, Заполним соответствующий сегмент: 1300 – 1000 = 300

(Леннон & Маккартни & Старр) | (Леннон & Маккартни & Харрисон) – это объединение заштрихованных сегментов из двух предыдущих диаграмм, следовательно, результат равен 1000 + 300 + 100 = 1400
Ответ: 1400
Задача 4.3.5. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос
|
Найдено страниц
(в тысячах)
|
|
лук | арбалет
|
426
|
|
лук | чеснок
|
414
|
|
арбалет & чеснок
|
0
|
|
лук | арбалет | чеснок
|
480
|
Какое количество страниц (в тысячах) будет найдено по запросу «лук»?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решайте с помощью кругов Эйлера и составления системы уравнений.
Нарисуем круги Эйлера. Заполним нулями сегменты «арбалет & чеснок = 0». Остальные сегменты обозначим буквами:

По исходным данным составим систему уравнений:
b + c + d + e = 426
a + b + c + d = 414
a + b + c + d + e = 480
Получилась система из трех уравнений с пятью неизвестными. Это означает, что не все сегменты можно найти. Поскольку мы ищем «Лук», то
b + c + d = ?
Обозначим b + c + d = x. Тогда система примет вид:
x + e = 426
a + x = 414
a + x + e = 480
Сложим второе и первое уравнения:
a + x + x + e = 414 + 426
Вычтем из полученного уравнения третье и получим x:
x = 414 + 426 – 480 = 360
Ответ: 360
Задача 4.3.6. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
|
Запрос
|
Найдено страниц
(в тысячах)
|
|
Козерог
|
522
|
|
Щука
|
700
|
|
Козерог | Лебедь
|
1446
|
|
Щука | Лебедь
|
1125
|
|
Козерог | Щука
|
1222
|
|
Лебедь | Щука | Козерог
|
1543
|
Какое количество страниц (в тысячах) будет найдено по запросу «Козерог & Лебедь»?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Рассмотрим сперва строчки условия:
|
Запрос
|
Найдено страниц
(в тысячах)
|
|
Козерог
|
522
|
|
Щука
|
700
|
|
Козерог | Щука
|
1222
|
Построим для них круги Эйлера и составим систему уравнений:

x + y = 522
y + z = 700
x + y + z = 1222
Сложим первое и второе уравнения:
x + y + y + z = 522 + 700
x + y + y + z = 1222
Вычтем из полученной суммы третье уравнение:
y = 0
Построим полную диаграмму Эйлера и обозначим неизвестные сегменты буквами:

Составим систему уравнений:
- a + b = 522
- e + d = 700
- a + b + c + d = 1446
- b + c + d + e = 1125
- a + b + d + e = 1222
- a + b + c + d + e 1543
Эта система уравнений избыточна для поиска b, соответствующего Козерог & Лебедь
Вычтем из шестого уравнения четвертое:
a = 1543 – 1125 = 418
Подставим а в первое уравнение и получим b:
b = 522 – a = 522 – 418 = 104
Ответ: 104
Круги Эйлера и логика применяются и в задачах на электронные таблицы.
Задача 4.3.7. На предприятии работают 100 человек. Каждый из них владеет как минимум одним иностранным языком (английским, немецким или французским). На следующей диаграмме отражено количество человек, владеющих каждым из языков.
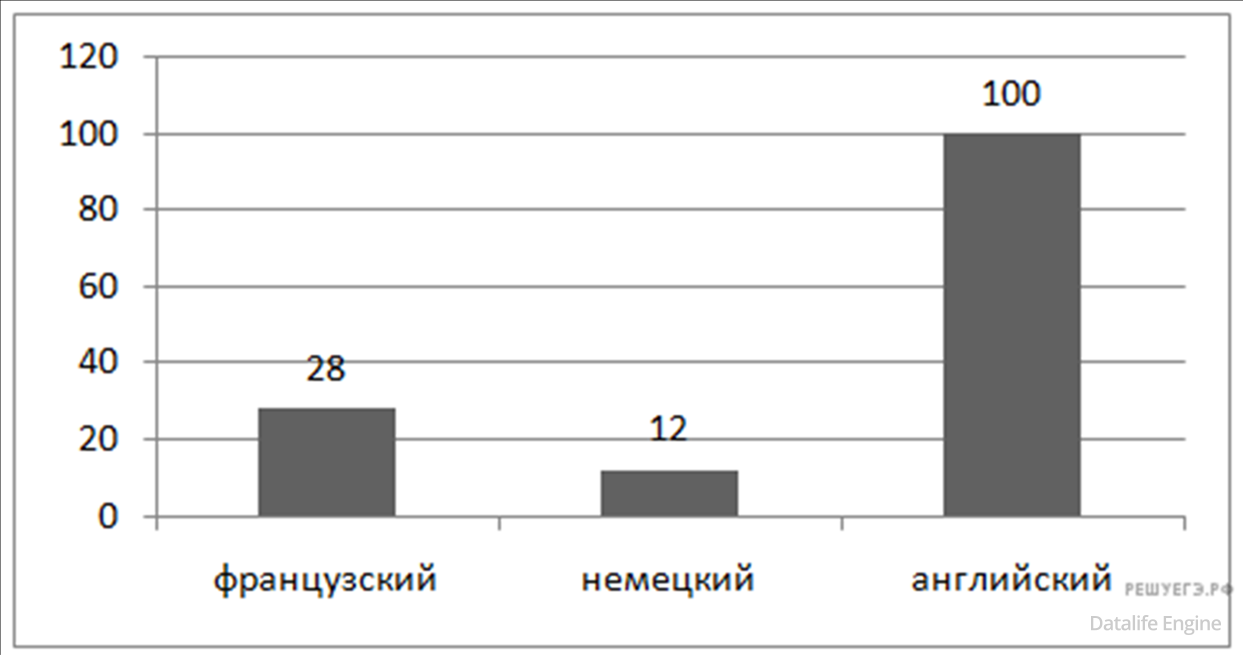
Вторая диаграмма отражает количество человек, знающих только один язык, только два языка или все три иностранных языка.
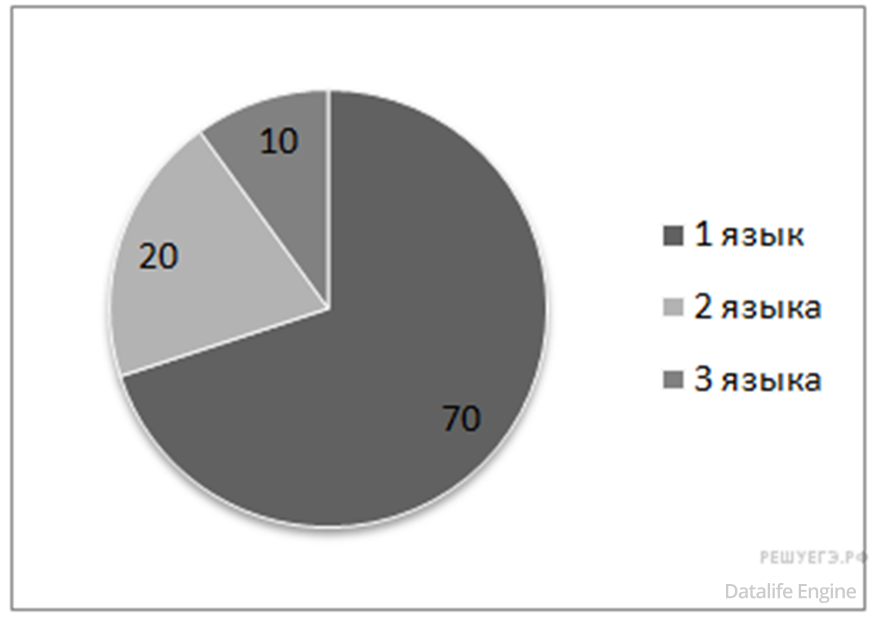
Определите количество человек, владеющих только английским языком, если говорят на английском и немецком, но не знают французского 2 человека.
Нарисуйте круги Эйлера для английского, французского и немецкого и начните их заполнять.
Построим круги Эйлера:
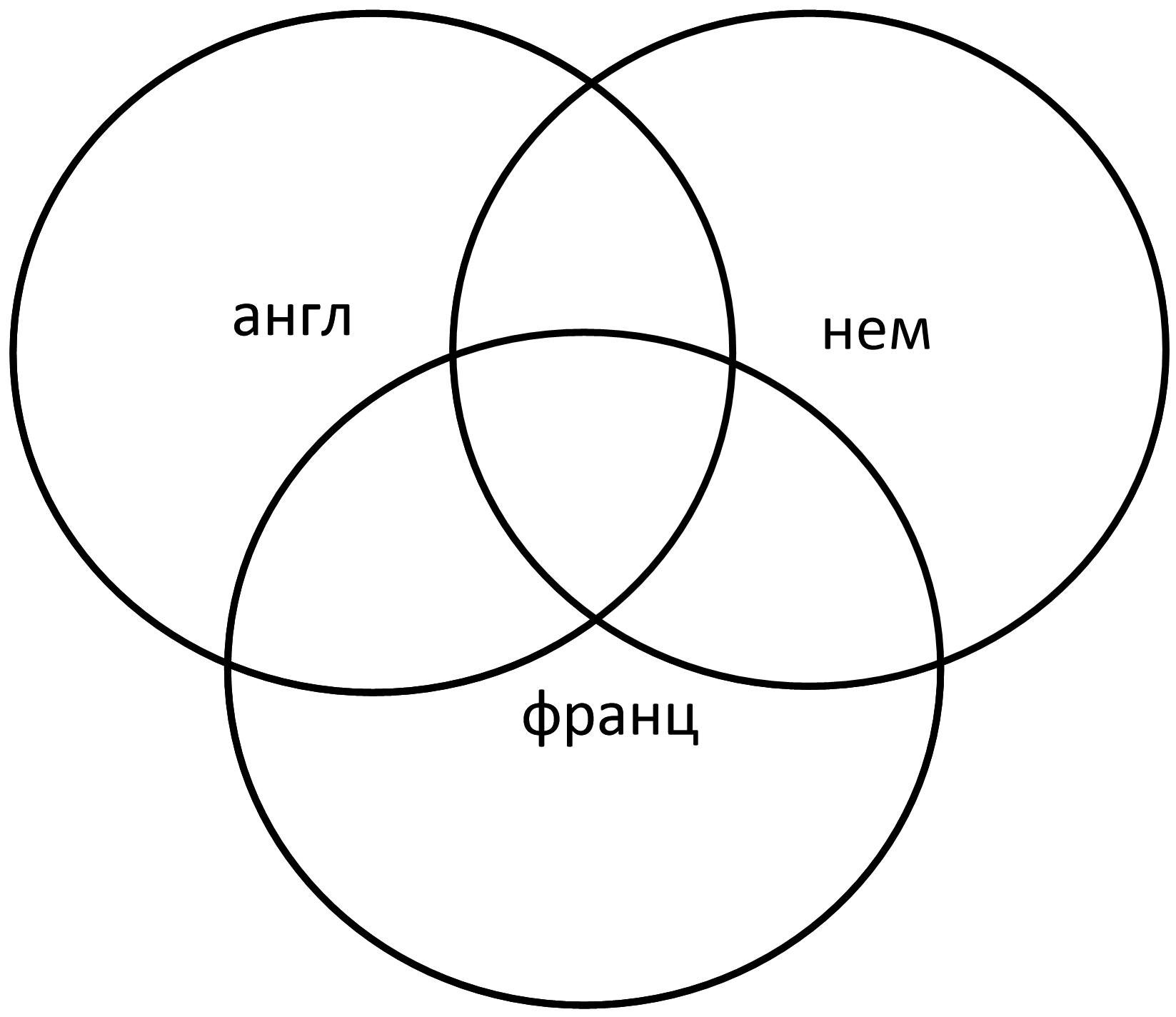
Из второй диаграммы видно, что на трех языках говорят 10 человек:
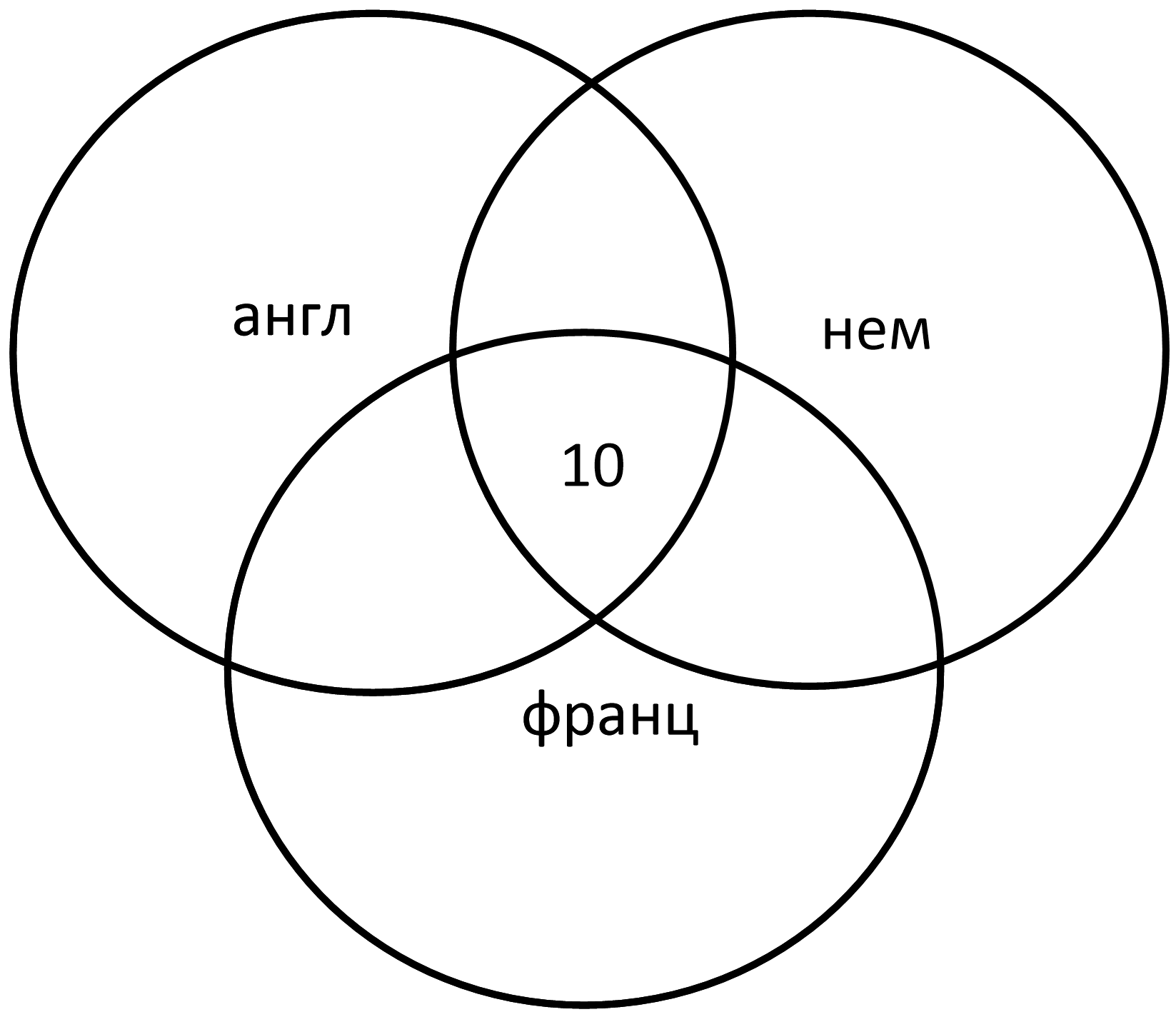
Говорят на английском и немецком, но не знают французского 2 человека:
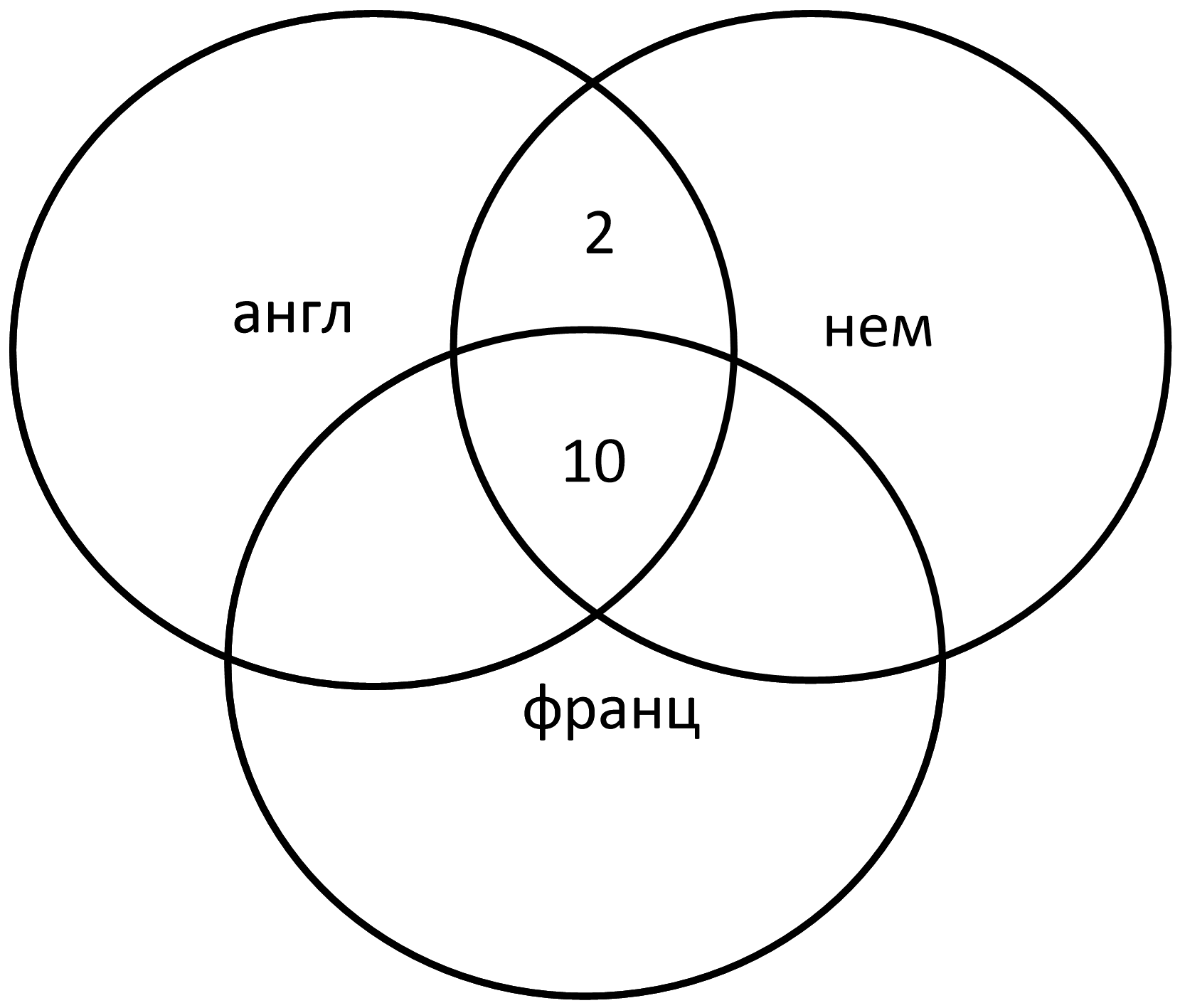
Из первой диаграммы говорят на немецком 12 человек. Но эти 12 человек мы уже записали на кругах Эйлера: 12 = 10 + 2. Значит, в оставшихся «немецких» сегментах 0:
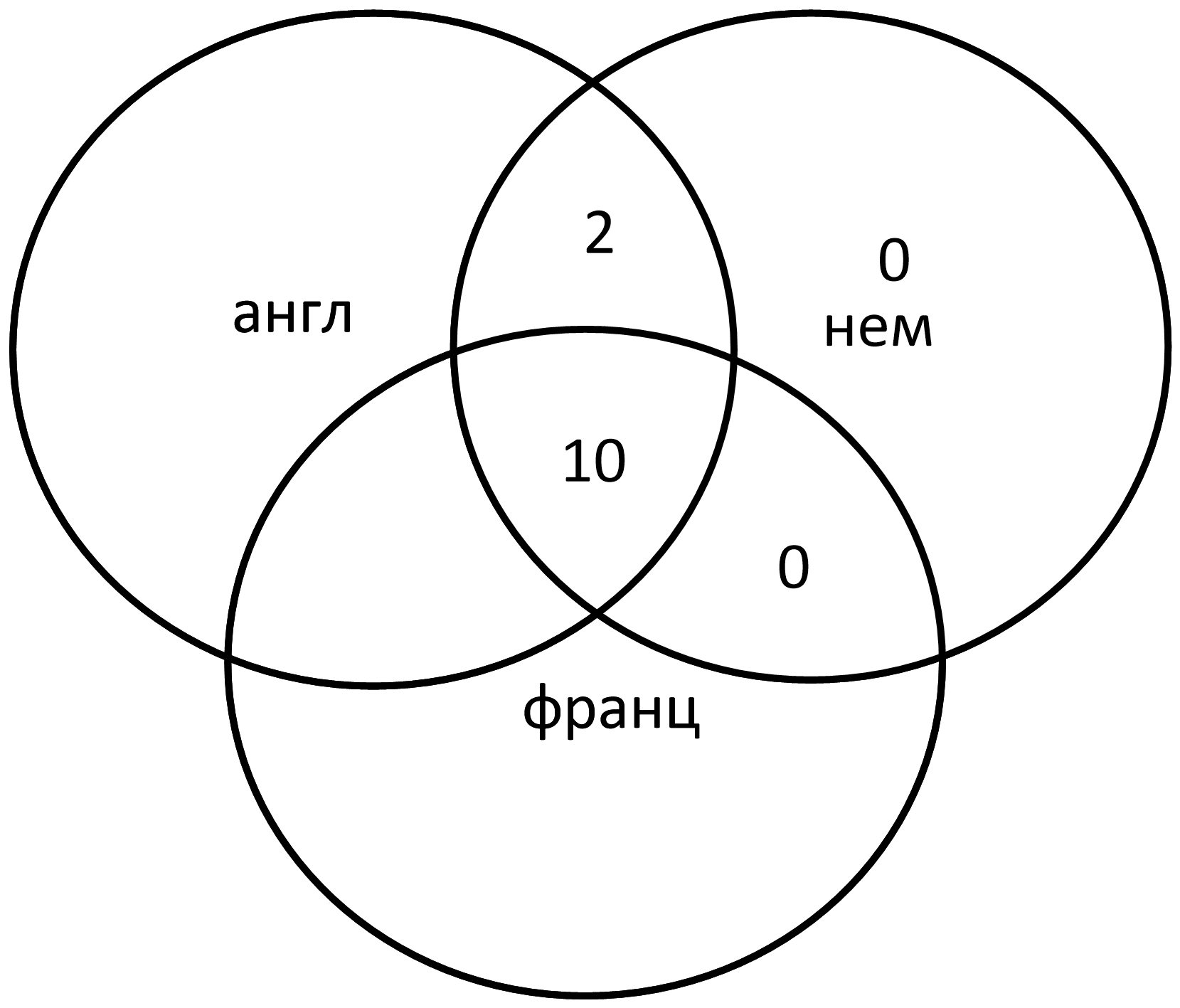
Из второй диаграммы на двух языках говорят 20 человек. Двоих из них мы уже отметили на диаграмме. Остается 20 – 2 = 18:

Из первой диаграммы по-французски говорят 28 человек, но мы их уже отметили: 28 = 18 + 10. Следовательно, в оставшемся французском секторе 0:
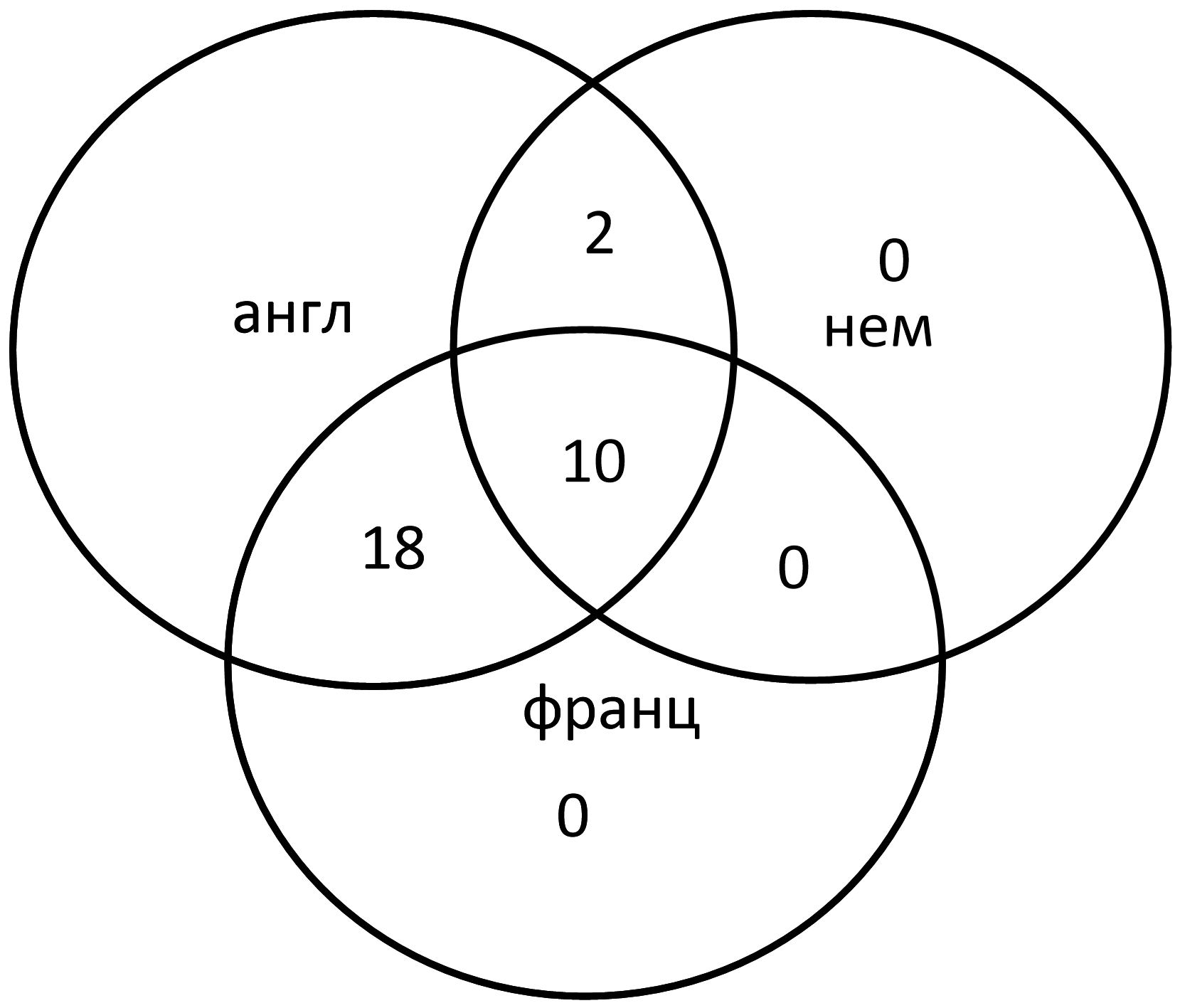
Из первой диаграммы на английском говорят 100 человек. С учетом уже заполненных «английских» сегментов только по-английски говорят: 100 – 18 – 10 – 2 = 70 человек.

Теперь мы имеем полную языковую картину на фирме.
Ответ: 70
Задача 4.3.8. Все ученики старших классов (с 9-го по 11-й) участвовали в школьной спартакиаде. По результатам соревнований каждый из них получил от 0 до 3-х баллов. На диаграмме I отражено распределение учеников по классам, а на диаграмме II — количество учеников, набравших баллы от 0 до 3-х. На обеих диаграммах каждый ученик учтён только один раз.
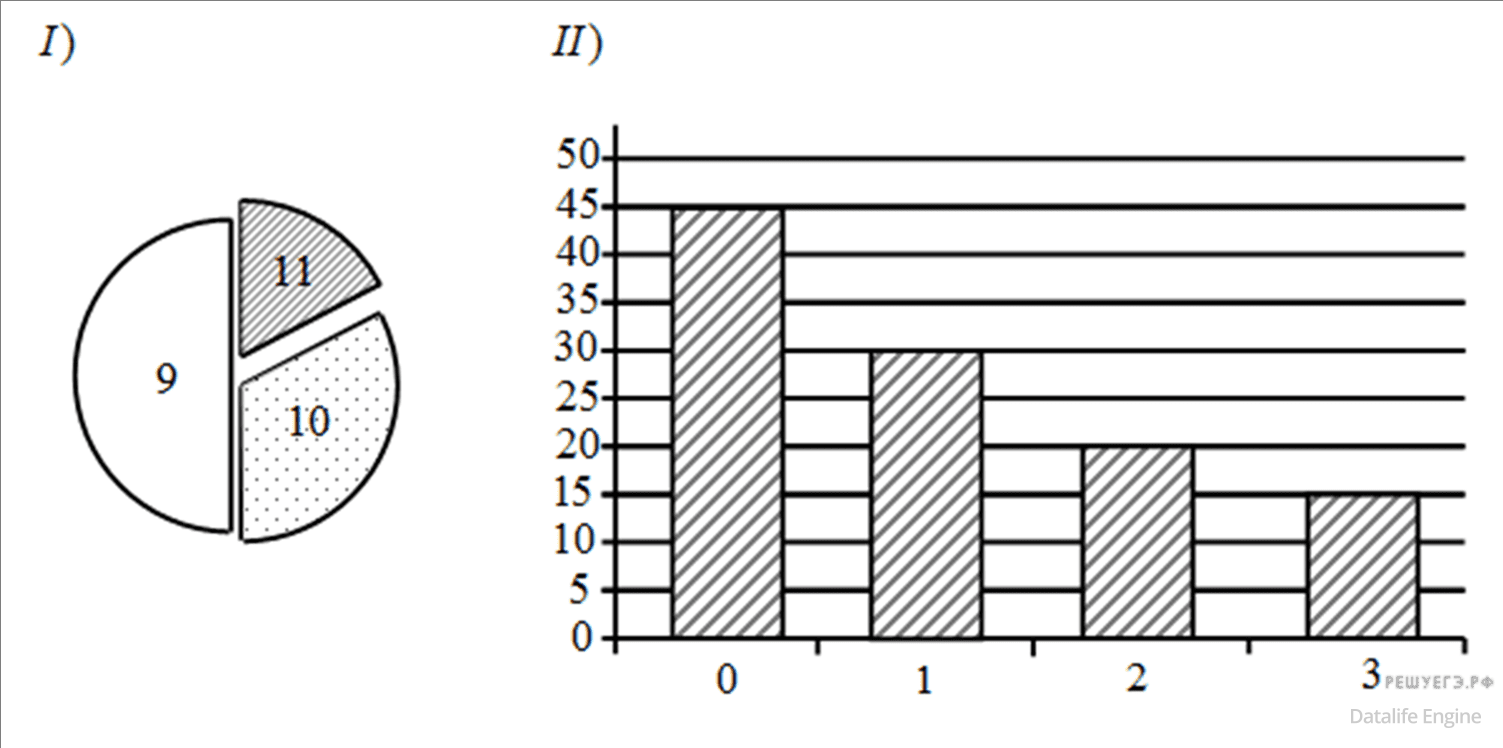
Имеются четыре утверждения:
1) Среди учеников 9-го класса есть хотя бы один, набравший 2 или 3 балла.
2) Все ученики, набравшие 0 баллов, могут быть 9-классниками.
3) Все 10-классники могли набрать ровно по 2 балла.
4) Среди набравших 3 балла нет ни одного 10-классника.
Какое из этих утверждений следует из анализа обеих диаграмм?
Сперва по диаграммам определите, сколько учеников учится в каждом классе. Потом анализируйте высказывания.
По второй диаграмме определим, сколько всего учеников:
45 + 30 + 20 + 15 = 110
Из первой диаграммы следует, что девятиклассников – половина: 110/2 = 55
Десятиклассников примерно ¾ от оставшейся половины: 41,
Одиннадцатиклассников: 14
Проанализируем первое утверждение: «Среди учеников 9-го класса есть хотя бы один, набравший 2 или 3 балла».
Учеников, набравших 0 и 1 балл 45 + 30 = 75 > 55.
То есть все девятиклассники могли набрать 0 или 1 балл и, возможно, нет ни одного девятиклассника, набравшего 2 или 3 балла.
style="font-size: 19px; font-family: 'Times New Roman', serif; text-indent: 0cm; text-align: justify; margin: 0cm 0cm 4pt 0cm;">
Проанализируем второе утверждение: «Все ученики, набравшие 0 баллов, могут быть 9-классниками».
Девятиклассников 55, учеников с 0 баллов только 45 < 55. Такое вполне возможно.
Проанализируем третье утверждение: «Все 10-классники могли набрать ровно по 2 балла».
Десятиклассников примерно 41, двухбалльников – 20<41. Следовательно, около 41-20=21 десятиклассников набрали отличные от 2 баллы.
style="font-size: 19px; font-family: 'Times New Roman', serif; text-indent: 0cm; text-align: justify; margin: 0cm 0cm 4pt 0cm;">
Проанализируем четвертое утверждение: «Среди набравших 3 балла нет ни одного 10-классника».
Из диаграмм не видно, что это так. 10-классники вполне могли набирать любые баллы.
Ответ: 2
style="font-size: 19px; font-family: 'Times New Roman', serif; text-indent: 0cm; text-align: justify; margin: 0cm 0cm 4pt 0cm;">
Диаграммы, как правило, строятся на основе электронных таблиц. Мы пока не будем отвлекаться от логики и перейдем к текстовым задачам и логическим уравнениям. Электронные таблицы изучим в другой главе.































