Образовательный портал Павла Добряка

Вспомним комбинаторику. У нас имеются 4 переменных, которые могут принимать значения 0 и 1. Сколько различных наборов переменных (то есть строчек в таблице истинности) существует? Если забыли, решайте задачу 2.2.1.

Количество наборов равно 2⁴ = 16, то есть не так много. Можно и составить таблицу истинности. Но это неинтересно. Начнем рассуждать, исходя из свойств логического «или». Чтобы получить истинное значение, нам подходят следующие значения выражений в скобках:

Скобка 1	Скобка 2
0	1
1	0
1	1

Выражения в скобках представляют собой «логическое и», которое равно 0 в трех случаях, а 1 – в одном:

A	B	A ∧ B
0	0	0
0	1	0
1	0	0
1	1	1

 

Напишем количество решений для каждой скобки:

Скобка 1		Скобка 2
значение	Кол-во решений	значение	Кол-во решений
0	3	1	1
1	1	0	3
1	1	1	1

 

Что нужно сделать, чтобы посчитать общее количество решений?

Ошибка. Если вы начали считать 3 + 1 = 4, то вы ошиблись. 

Продолжение хода решения.

Допустим, значение первой скобки – 0, то есть три решения:

К	L	K ∧ L
0	0	0
0	1	0
1	0	0

Возьмем соответствующую строчку из второй скобки:

M	N	M ∧ N
1	1	1

Решением уравнения называется полный набор переменных:

К	L	M	N
0	0	1	1
0	1	1	1
1	0	1	1

 

То есть количества решений в разных скобках не складываются, а умножаются:

Скобка 1		Скобка 2		Общее Кол-во решений
значение	Кол-во решений	значение	Кол-во решений
0	3	1	1	3
1	1	0	3	3
1	1	1	1	1
Всего				7

 

Проверим наши подсчеты, составив таблицу истинности:

К	L	M	N	(K ∧ L) ∨ (M ∧ N)
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	1
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

 

Ответ: 7

Попробуйте сначала упростить выражение, потом посчитайте количество вариантов в первой скобке.

Выражение вида (N ∨ ⌐N) – верный признак, что нужно упрощать. Составим для него таблицу истинности:

N	⌐N	N ∨ ⌐N
0	1	1
1	0	1

 

Выражение N ∨ ⌐N тождественно равно единице, поэтому:

(J ∨ ⌐K ∨ L ∨ ⌐M) ∧ (N ∨ ⌐N) = (J  ∨ ⌐K ∨ L ∨ ⌐M) ∧ 1 =  (J  ∨ ⌐K ∨ L ∨ ⌐M)

Уравнение после упрощения приобретает вид:

J ∨ ⌐K ∨ L ∨ ⌐M = 1.

Посчитайте количество строк в таблице истинности. Если у вас возникли затруднения, смотрите предыдущую задачу. Количество строк равно 16. По свойству «логического или» только одна строчка дает ответ 0:

J	К	L	M	J     ∨ ⌐K ∨ L ∨ ⌐M
0	1	0	1	0

Остальные 15 дают 1.

Ошибка. Если вы считаете 15 ответом, то вы ошибаетесь. Ведь существует только 15 наборов переменных J, K, L, M. Но ответом уравнения является набор всех переменных. У нас есть еще N, и не важно, что N исчезло при упрощении выражения. Это означает лишь то, что N может принимать любое значение: 0 и 1. Если вы считаете ответом 15 + 2 = 17, то вы опять ошиблись (см. предыдущую задачу).

Продолжение хода решения.

Итак, у нас есть 15 наборов J, K, L, M и 2 набора N. При соединении наборов у нас каждый набор из J, K, L, M в ответе будет два раза – с N = 0 и N = 1. Вот фрагмент таблицы истинности:

J	К	L	M	N
0	1	0	0	0
0	1	0	0	1
0	1	1	0	0
0	1	1	0	1
0	1	1	1	0
0	1	1	1	1

Такое соединение наборов называется в математике декартовым произведением.

Всего решений уравнения – 15 * 2 = 30.

Ответ: 30

Cначала упростите выражение, потом стройте дерево решений, например, как в задаче 2.5.4. на условие Фано в неравномерном коде.

(⌐J ∨ K) = J → K

По закону де Моргана вынесем отрицание перед крупными скобками:

⌐(((J → K) → (L ∧ M ∧ N)) ∧ ((L ∧ M ∧ N) → (⌐J ∨ K))) ∨ (M ∧ J) = 0

Обратите внимание, что переменные образуют группы. Можно воспользоваться формулой

(A → B) ∧ (B → A) = (A ≡ B)

Получим выражение:

⌐((J → K) ≡ (L ∧ M ∧ N)) ∨ (M ∧ J) = 0

Логическое «или» равно 0, когда все «слагаемые» равны 0:

⌐((J → K) ≡ (L ∧ M ∧ N)) = 0

M ∧ J = 0

 

Запишем по-другому:

(J → K) ≡ (L ∧ M ∧ N) = 1

M ∧ J = 0

Теоретически дерево решений можно начинать строить с любой переменной, но в этой задаче удобнее начать с J, так как с J начинается первое уравнение и J фигурирует во втором:

Далее выберем переменную К. О её значениях в каждой ветке мы пока ничего сказать не можем, поэтому:

Нарушим алфавитный порядок и выберем M, так как M фигурирует в обоих уравнениях. В правой стороне дерева J = 0, значит, второе уравнение равно 0 и не накладывает ограничения на M.

В крайней левой ветке J = 0, К = 0, значит J → K = 1, потому:

L ∧ M ∧ N = 1, это возможно, только если все переменные равны 1:

Во второй слева ветке J = 0, К = 1, значит J → K = 1. Вторая ветка аналогична первой ветке:

В правой части дерева J = 0, следовательно, по второму уравнению М = 0:

В третьей ветке J = 1, К = 0, следовательно, J → K = 0, значит и L ∧ M ∧ N = 0. Поскольку в этой же ветке мы уже определили, что М = 0, то на L и N не налагается никаких ограничений. То есть по этой ветке 4 решения:

Осталось рассмотреть последнюю ветку. J = 1, К = 1, значит, J → K = 1, следовательно, 

L ∧ M ∧ N = 1. Но это невозможно, так как мы уже определили, что здесь М = 0. Это противоречие, поэтому ветка не имеет решений:

Веток, которые дошли до конца, то есть которые представляют собой полные наборы переменных, 6. Это и является ответом.

Ответ: 6

Прежде чем строить дерево, введите новые обозначения.

Обратите внимание, что переменные образуют устойчивые группы выражений. Например, (x3 ≡ x4) присутствует в первом и втором уравнении, переменные x3 и x4 больше в других скобках не встречаются. Так же, как и в алгебре, можно ввести новые обозначения для таких групп переменных:

y1 = (x1 ≡ x2)

y2 = (x3 ≡ x4)

y3 = (x5 ≡ x6)

y4 = (x7 ≡ x8)

y5 = (x9 ≡ x10)

Система уравнений примет вид:

у1 ≡ y2 = 0

у2 ≡ y3 = 0

у3 ≡ y4 = 0

у4 ≡ y5 = 0

Ложь психологически искать тяжело, так как люди привыкли искать истину, поэтому преобразуем уравнения:

у1 ≠ y2 = 1

у2 ≠ y3 = 1

у3 ≠ y4 = 1

у4 ≠ y5 = 1

 

Строим дерево. Так как следующий номер y должен отличаться от предыдущего, мы получим две ветки с чередующимися значениями:

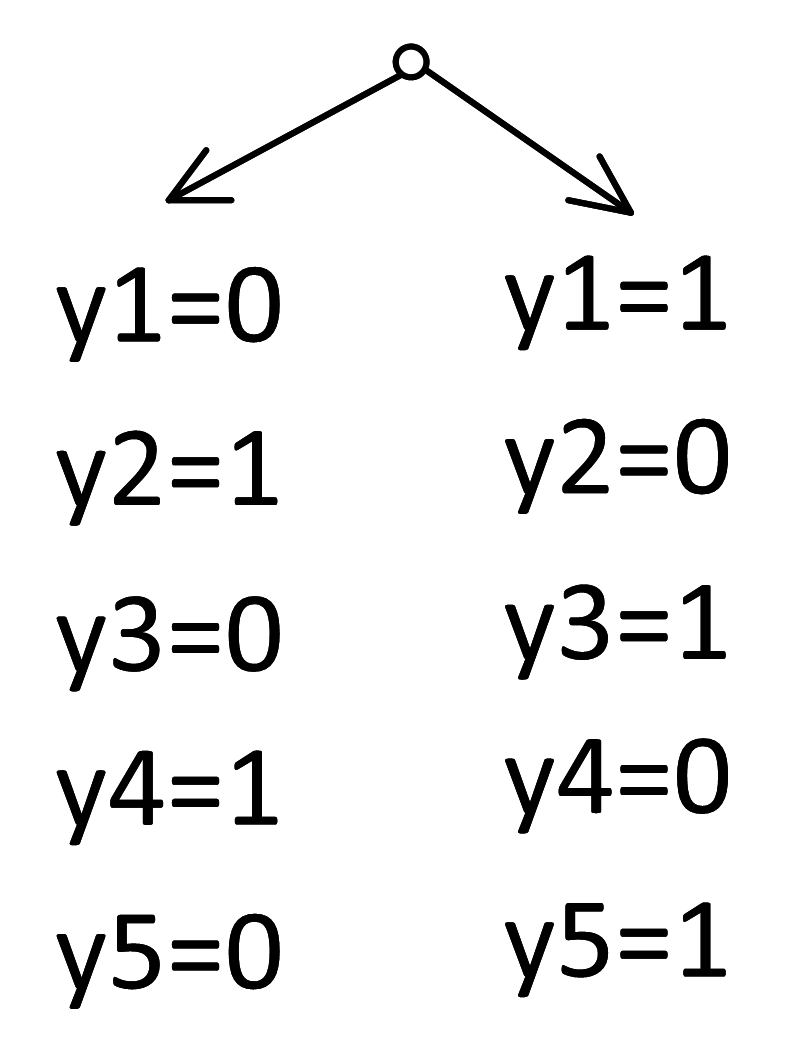
Теперь нужно вернуться обратно к переменным x.

Посчитаем, сколько переменных x соответствует каждому узлу y.

Рассмотрим y1 = 0

x1 ≡ x2 = 0

 

x1	x2	x1 ≡ x2
0	1	0
1	0	0

Два решения.

 

Аналогично два решения для узла y1 = 1

x1 ≡ x2 = 1

x1	x2	x1 ≡ x2
0	0	1
1	1	1

 

Припишем количество решений в каждый узел дерева y

Сколько же всего решений?

Ошибка. Если вы посчитали по каждой ветке количество решений как 2 + 2 + 2 + 2 + 2 = 10, то вы ошиблись (см. ошибку в прошлой задаче).

Продолжение хода решения.

Из прошлой задачи мы знаем, что, когда к множеству одних переменных добавляется другая переменная, то наборы соединяются как декартово произведение – все наборы из одного множества переменных соединяются со всеми наборами других переменных. А количество решений вычисляется как произведение.

То есть по одной ветке 2 * 2 * 2 * 2 * 2 = 32. Поскольку веток две, 32 + 32 = 64:

Ответ: 64.

Упростить уравнение нельзя, ввести новые обозначения тоже. Начните строить дерево и найдите в нем закономерность.

Начнем строить дерево по первому уравнению:

Из уравнения видно, что когда у нас подряд идут одинаковые x,

00

11

то x1 ≡ x2 истинно, значит, истиной должно быть и следующее тождество, поэтому эти ветки перестают ветвиться и продолжаются так до конца:

000…0

111…1

Возьмем еще одно уравнение:

Похоже, что на каждом уровне ветвятся только две ветки – одна с правой стороны, другая – с левой. Поэтому на каждом уровне добавляется по два решения. Проверим это предположение, нарисовав еще один уровень:

Предположение подтвердилось.  Дальше строить дерево необязательно. Рассмотрим левую часть дерева. По уровням решения образуют ряд: 1, 2, 3, 4, 5… . Таким образом, с левой стороны на 8 уровне будет 8 решений. Аналогично на правом уровне. Всего 8 + 8 = 16 решений.

Ответ: 16

Постройте дерево для первых двух уравнений и определите, как каждое следующее уравнение влияет на количество решений.

Построим дерево для первого уравнения:

Добавим второе уравнение. Обратите внимание, что порядок появления новых переменных отличен от предыдущей задачи. Там индексы переменных шли плотно:

1. 123
2. 234
3. 345
4. 456

В этом же уравнении:

1. 123
2. 345
3. 567
4. 789

 

Поэтому уровни надо добавлять сразу по 2, поскольку каждое следующее уравнение зависит только от нижнего уровня построенного дерева и добавляет две новых переменных:

Ошибка. Ошибкой было бы смотреть на каждом уровне количество решений и пытаться вывести закономерность: 2, 4, 6, 12, 18. Так закономерность не увидеть. Надо смотреть через ряд – по уравнениям: 6, 18, 54

Продолжение хода решения.

Каждый узел x3 порождает веточки, такие же, как и на уровне x1. Есть два вида веточек – идущие из 0 и идущие из 1. Дальше всё будет повторяться точно так же (рассмотрим фрагмент):

Таким образом, каждое дополнительное уравнение утраивает количество решений:

2 * 3 * 3 * 3 * 3 = 162.

Ответ: 162.

Решение этой системы уравнений повторяет все изученные приемы: упрощение выражения, введение новых обозначений, поиск закономерности в дереве.

Выражения вида (x1 ∧ x2) ∨ (⌐x1 ∧ ⌐x2) – это признак того, что надо упрощать. Воспользуемся формулами, которые мы знаем:

По де Моргану:

(x1 ∧ x2) ∨ ⌐(x1 ∨ x2)

(x1 ∨ x2) → (x1 ∧ x2)

Дальше формул нам не хватает. В это случае составим таблицу истинности:

x1	x2	x1 ∨ x2	x1 ∧ x2	(x1∨ x2) → (x1∧ x2)
0	0	0	0	1
0	1	1	0	0
1	0	1	0	0
1	1	1	1	1

Это тождество!

x1 ≡ x2

Для второго уравнения сразу построим таблицу истинности:

(⌐x3 ∧ x4) ∨ (x3 ∧ ⌐x4)

x3	x4	⌐x3 ∧ x4	x3 ∧ ⌐x4	(⌐x3∧ x4) ∨ (x3∧ ⌐x4)
0	0	0	0	0
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Это «исключающее или» или отрицание тождества:

⌐(x3 ≡ x4)

Система примет вид:

(x1 ≡ x2) ∨ ⌐(x3 ≡ x4) = 1

(x3 ≡ x4) ∨ ⌐(x5 ≡ x6) = 1

(x5 ≡ x6) ∨ ⌐(x7 ≡ x8) = 1

…

(x13 ≡ x14) ∨ ⌐(x15 ≡ x16) = 1

Введем новые обозначения:

y1 = (x1 ≡ x2)

y2 = (x3 ≡ x4)

y3 = (x5 ≡ x6)

…

y8 = (x15 ≡ x16)

Система примет вид:

y1 ∨ ⌐y2 = 1

y2 ∨ ⌐y3 = 1

y3 ∨ ⌐y4 = 1

…

y7 ∨ ⌐y8 = 1

Построим дерево:

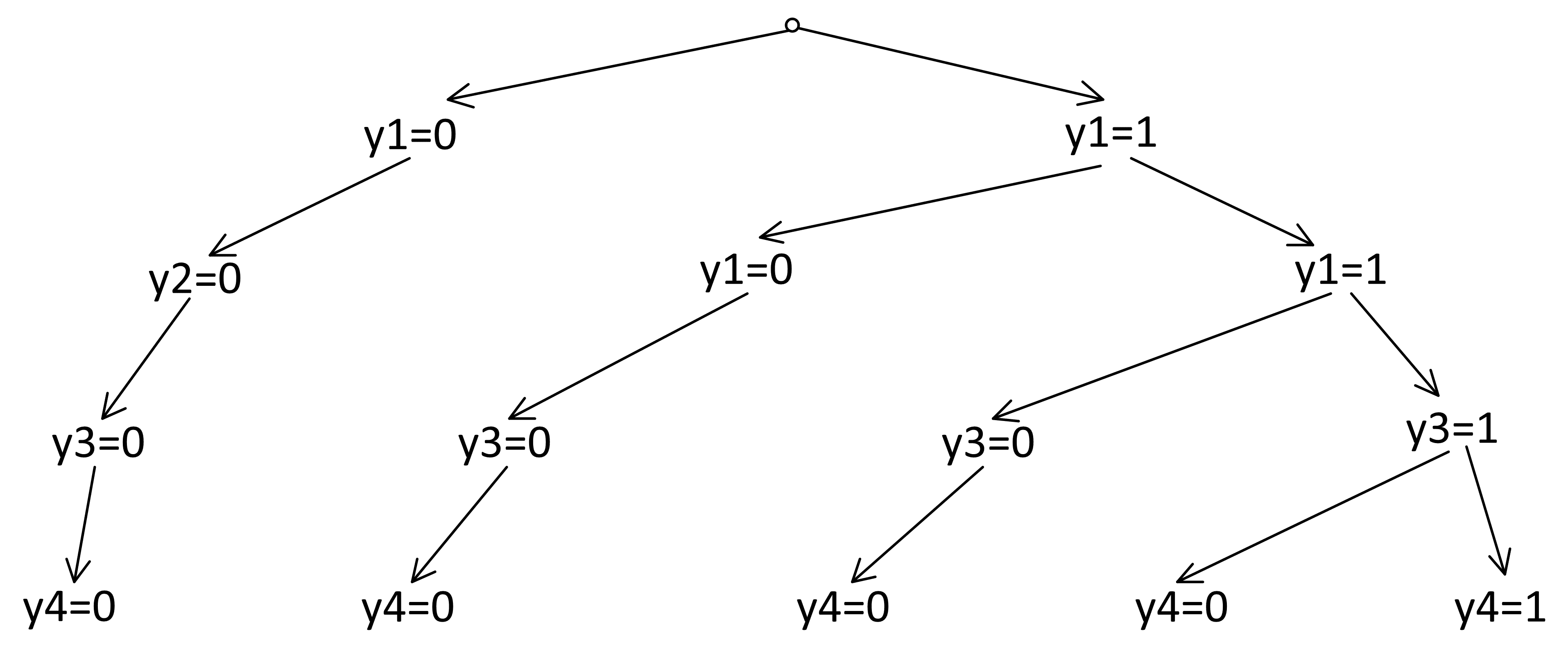
Закономерность видна: каждый уровень увеличивает количество решений на 1. На последнем, 8-м, уровне будет 9 решений. Но это только по y. А нам нужно вернуться к исходным обозначениям.

В задаче 4.4.4 мы уже рассматривали количество решений x в каждом узле y:

x1 ≡ x2 = 0

x1	x2	x1 ≡ x2
0	1	0
1	0	0

Два решения.

x1 ≡ x2 = 1

x1	x2	x1 ≡ x2
0	0	1
1	1	1

Два решения.

 

Дерево приобретает вид:

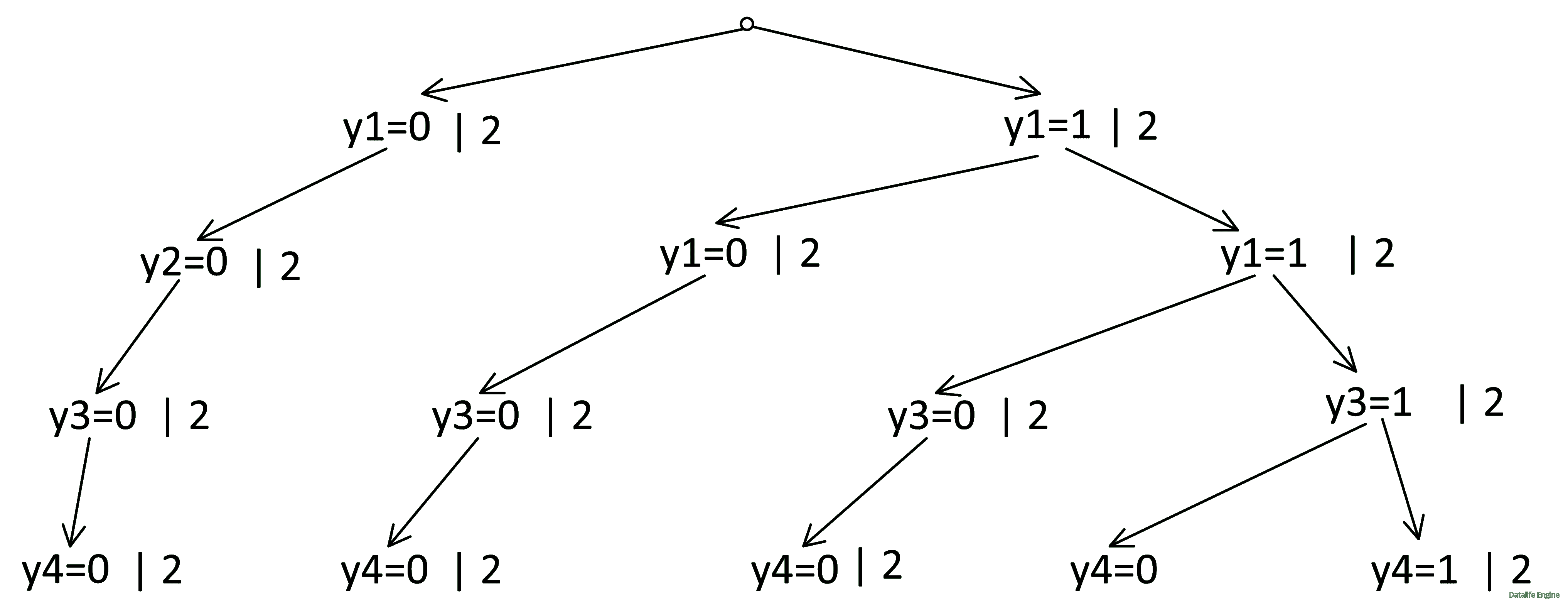
В каждой ветке y в каждом узле по 2 решения. Возвращаясь к x, каждая ветка y превращается в 2⁸ = 256 веточек x.

Всего решений x: 2⁸ = 9 * 256 = 2304 

Ответ: 2304

Несмотря на кажущуюся простоту, решить эту систему непросто. Начните строить дерево и обнаружьте закономерность. Далее придумайте способ обсчета дерева (несмотря на то, что закономерность прослеживается, формулы для вычисления нет).

Если начать строить дерево, как мы уже строили, то у нас будет много «мертвых ветвей» (см. задачу 4.4.3).

Рассмотрим два уравнения:

x1 ∨ x2 ∧ x3 = 1

x2 ∨ x3 ∧ x4 = 1

 

Чтобы первое уравнение было истинным, подходит набор 100:

1 ∨ 0 ∧ 0 = 1

 Но он уже не удовлетворяет второму уравнению:

0 ∨ 0 ∧ x4 = 0

Поэтому два нуля подряд в дереве идти не могут.

 

Сформулируем еще правило:

010 также невозможен:

0 ∨ 1 ∧ 0 = 0

Таким образом, допустимые цепочки:

011

110

111

Или в словесной форме:

1. После нуля идут две единицы
2. Две единицы на третьем уровне ветвятся.

Теперь можно строить дерево, вообще не обращая внимания на уравнения!

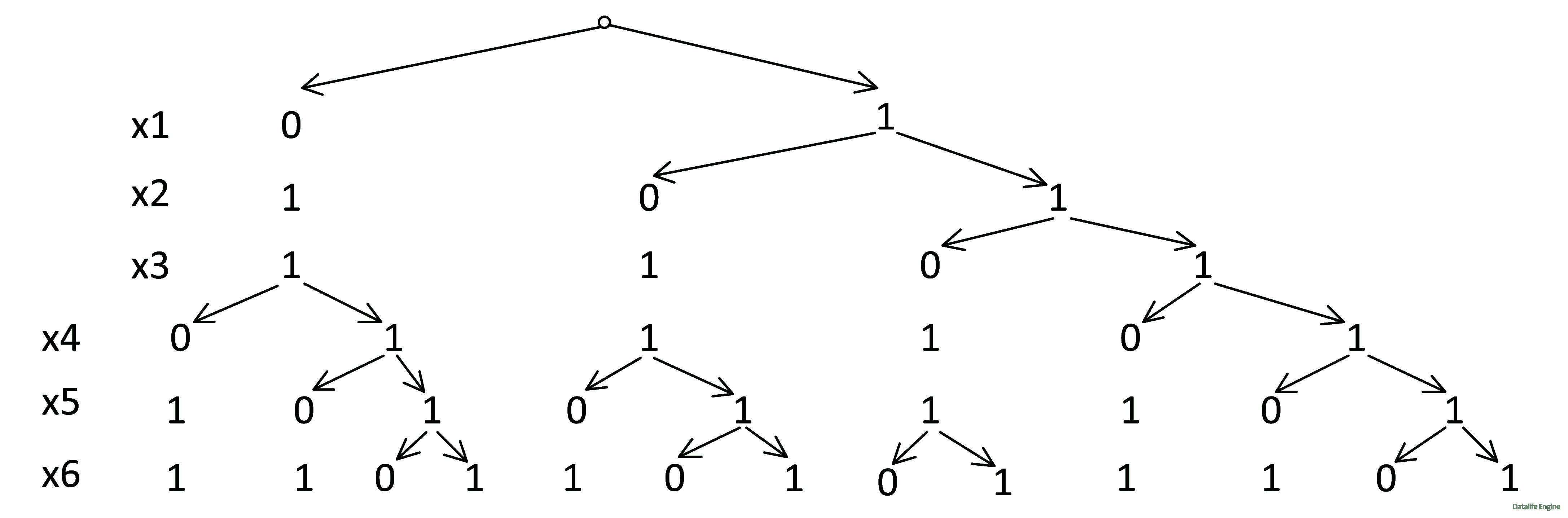
Дойдя до x6, мы видим, что левая ветка является «недоразвитой» копией правой. Кроме того, внутри веток рождаются новые ветки, которые подобны большим веткам. Такая структура в математике называется фракталом. Но если мы попробуем посчитать количество решений на каждом уровне, то мы увидим: 2, 3, 4, 6, 9, 13. Непонятно, как написать формулу.

Придумаем другой способ обсчета. Зная принцип построения дерева, на каждом уровне будем рисовать не дерево, а подсчитывать количество узлов разного вида. В дереве три вида узлов:

“0” неветвящийся

“1” неветвящийся

“1” ветвящийся

 

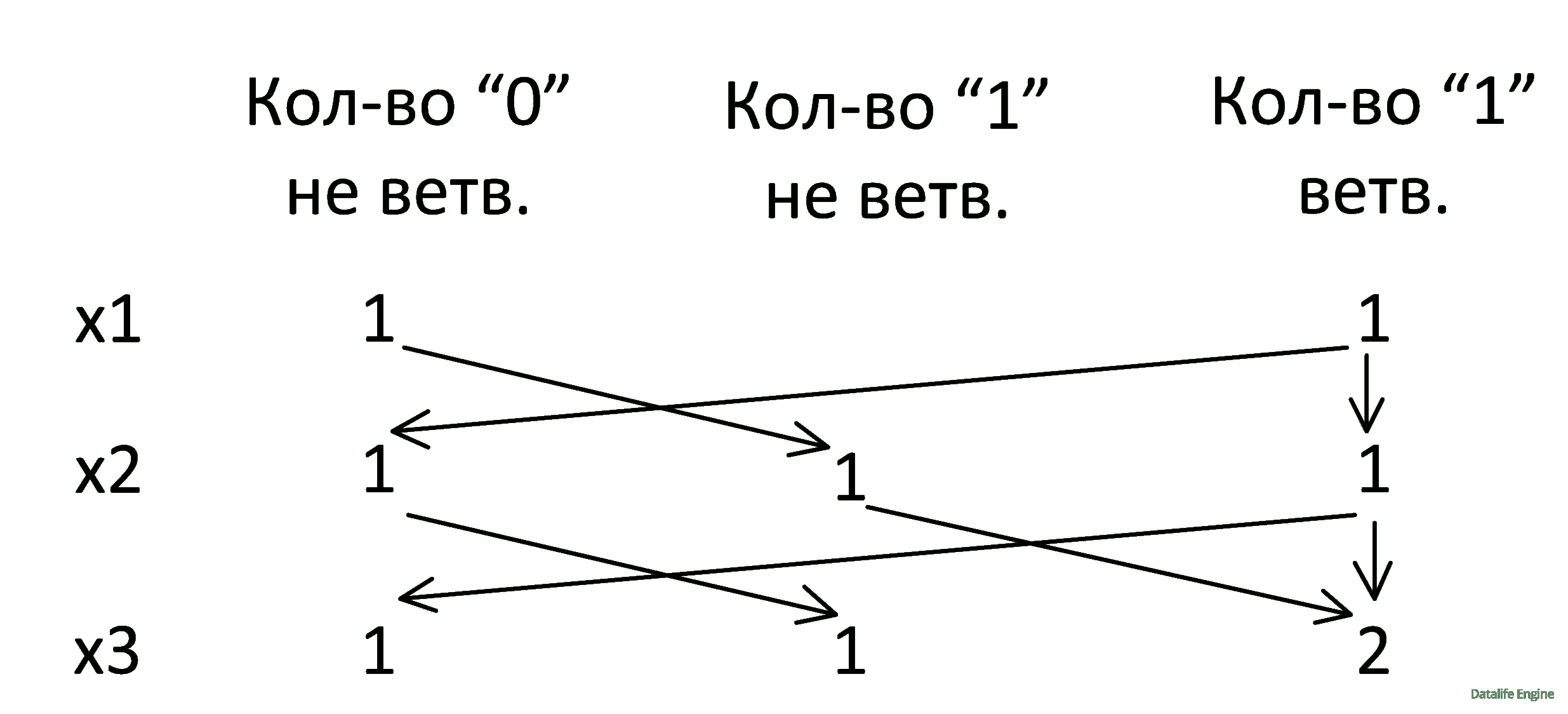
Рисунок подсчета будет повторяться:

1. Количество ветвящихся единиц на текущем уровне будет равно сумме количества неветвящихся единиц и количества ветвящихся единиц на предыдущем уровне.
2. Количество нулей на текущем уровне равно количеству ветвящихся единиц на предыдущем уровне.
3. Количество не ветвящихся единиц на текущем уровне равно количеству нулей на предыдущем уровне.

Продолжим делать подсчеты дальше:

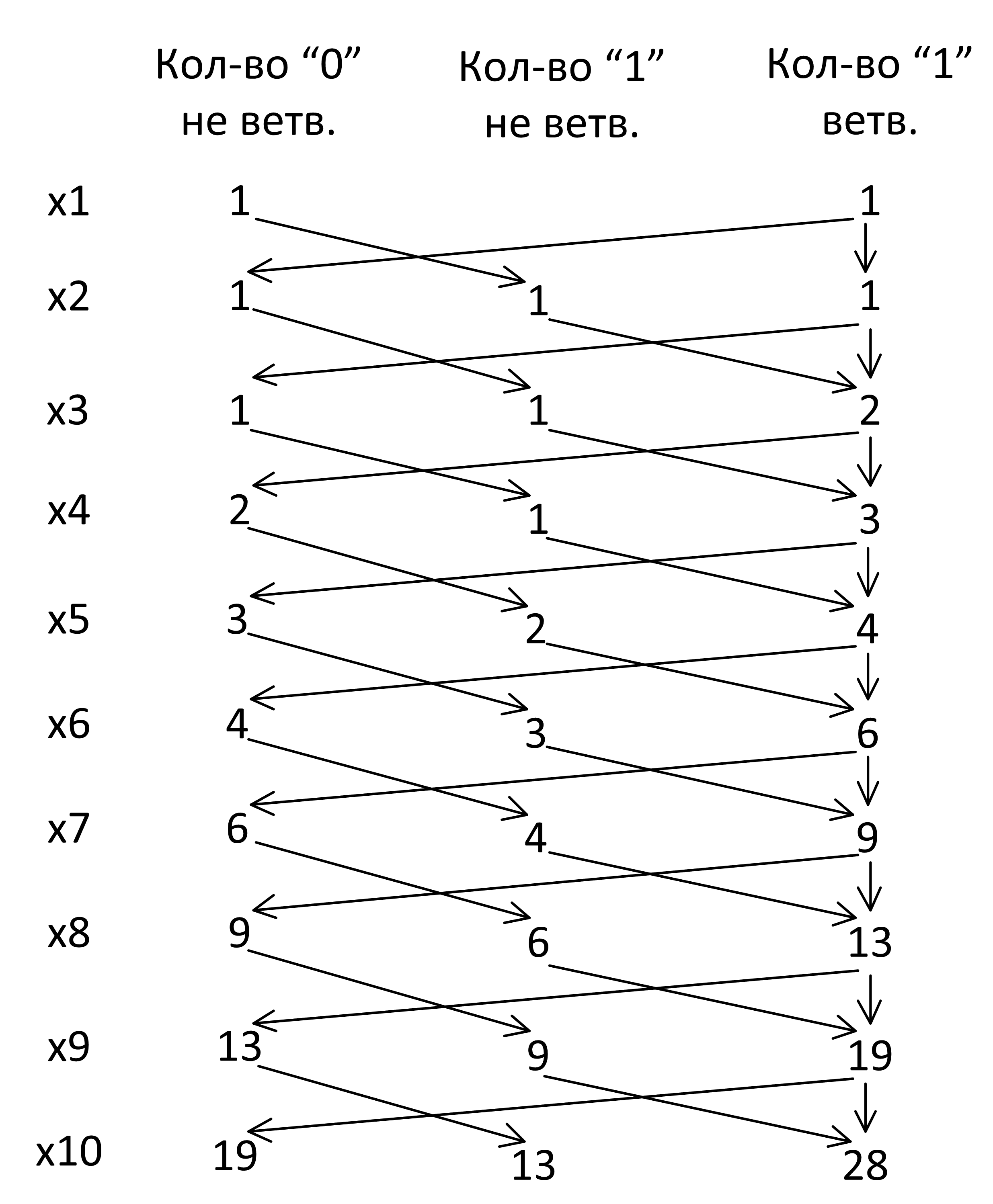
Ошибка. Если мы на этом остановимся и произведем подсчеты 19 + 13 + 28, то мы ошибемся, так как на нижнем уровне дерево «растет» по-другому

 

Продолжение хода решения.

Посмотрим на последнем уровне значения 100:

x8 ∧ x10 = 1 ∨ 0 ∧ 0 = 1.

То есть нули на предпоследнем уровне ветвятся!

Такое бывает, когда у нас есть «умирающие ветви». Мы записали правила построения дерева без подсчета умирающих ветвей. Но на последнем уровне они вовсе не умирают. Правильно было бы дерево рисовать так:

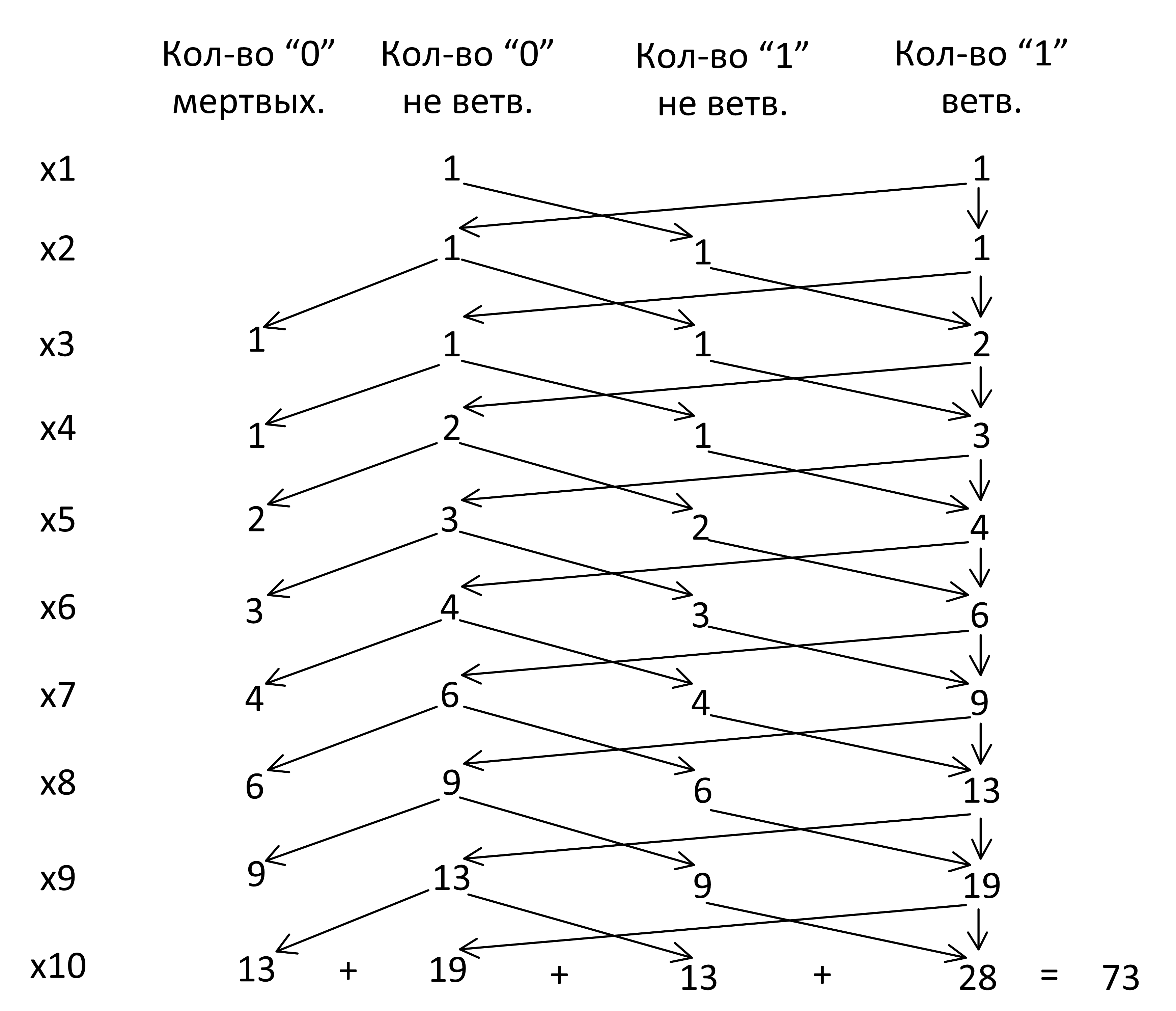
Ответ: 73

Постройте дерево для первого уравнения. Обратите внимание, что y и z за счет следующих уравнений привязаны только к x соответствующего номера. Поэтому можно обсчитать для каждого узла дерева x, сколько y и z там находится. А дальше действовать, как в задачах на новые обозначения.

Построим дерево для x. Введем правила для построения дерева. 

Поскольку следования соединены логическим «и», то каждое следование должно быть истинным.

Из 0 может следовать что угодно:

00

01

А вот из 1 только 1:

11

Таким образом, ноль ветвится, а единица – нет:

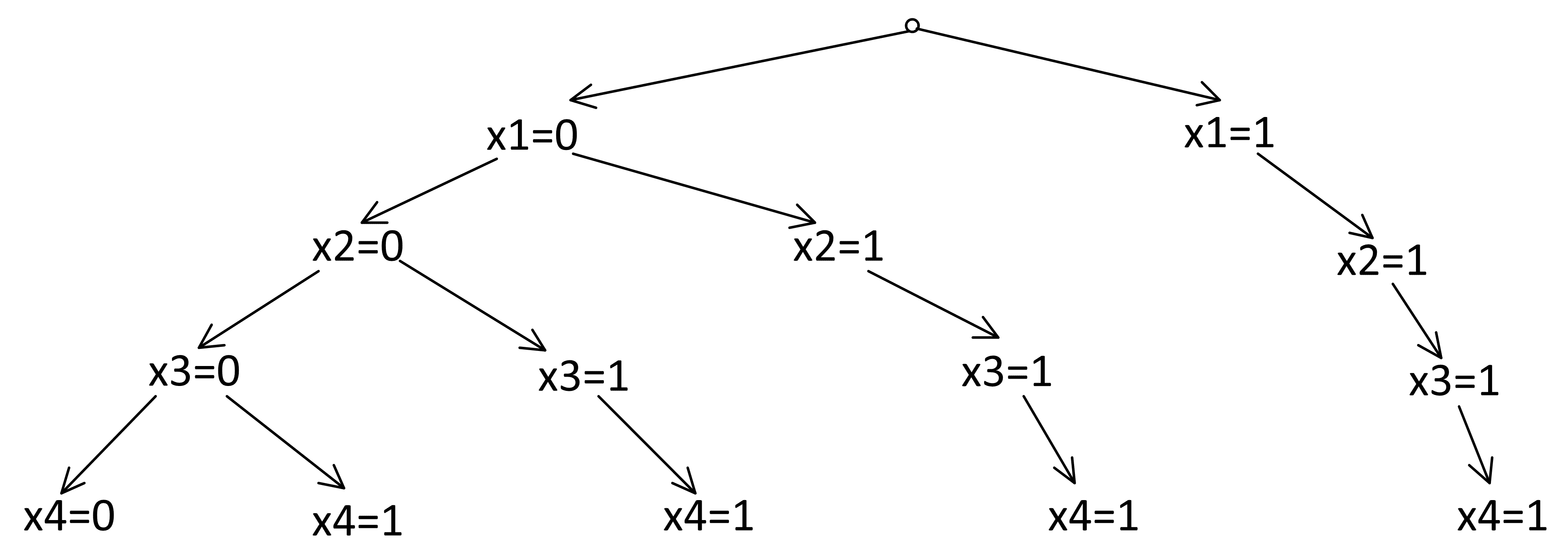
Посчитаем, сколько решений y и z находятся в узле x=0.

(¬x1 ∧ y1 ∧ z1) ∨ (x1 ∧ ¬y1 ∧ z1) ∨ (x1 ∧ y1 ∧ ¬z1) = 1

(1 ∧ y1 ∧ z1) ∨ (0 ∧ ¬y1 ∧ z1) ∨ (0 ∧ y1 ∧ ¬z1) = 1

(y1 ∧ z1) 0 ∨ 0 = 1

y1 ∧ z1 = 1

Уравнению соответствует 1 решение:

y1=1, z1 = 1

 

Посчитаем, сколько решений y и z находятся в узле x=1.

(¬x1 ∧ y1 ∧ z1) ∨ (x1 ∧ ¬y1 ∧ z1) ∨ (x1 ∧ y1 ∧ ¬z1) = 1

(0 ∧ y1 ∧ z1) ∨ (1 ∧ ¬y1 ∧ z1) ∨ (1 ∧ y1 ∧ ¬z1) = 1

0 ∨ (¬y1 ∧ z1) ∨ (y1 ∧ ¬z1) = 1

(¬y1 ∧ z1) ∨ (y1 ∧ ¬z1) = 1

 

Уравнению удовлетворяют два решения:

y1=0, z1 = 1

y1=1, z1 = 0

Припишем к узлам дерева, сколько в каждом узле есть решений, и сделаем обсчет:

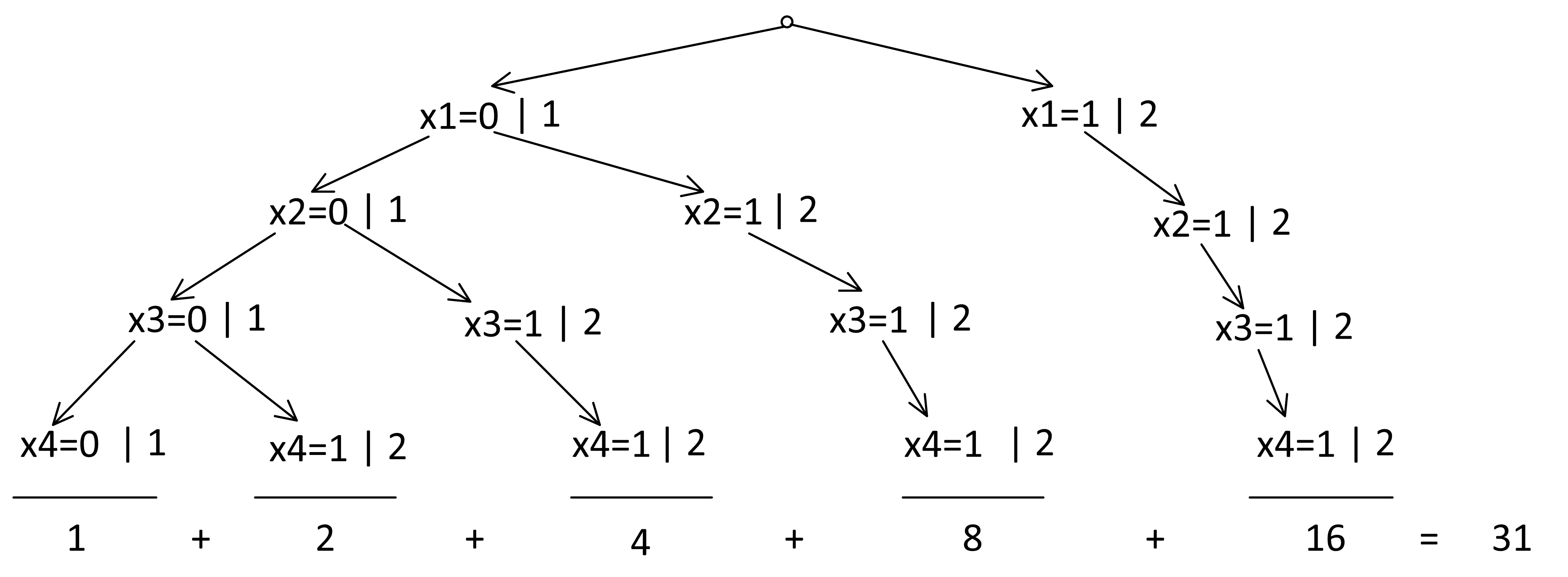
Ответ: 31

Постройте дерево для x. Посчитайте для каждого узла дерева, сколько ему соответствует решений y (см. задачу 4.4.9). 

Упростим уравнения, заменив:

¬x ∨ y на x → y:

(x1 ∨ x2) ∧ ((x1 ∧ x2) → x3) ∧ (x1 → y1) = 1

(x2 ∨ x3) ∧ ((x2 ∧ x3) → x4) ∧ (x2 → y2) = 1

…

(x6 ∨ x7) ∧ ((x6 ∧ x7) → x8) ∧ (x6 → y6) = 1

(x7 ∨ x8) ∧ (x7 → y7) = 1

(x8 → y8) = 1

 

Обратим внимание на то, что уравнения представляют собой «множители», соединенные логическим «и». Каждый множитель должен быть равен 1. Поэтому эти уравнения можно разбить на отдельные уравнения:

(x1 ∨ x2) ∧ ((x1 ∧ x2) → x3) = 1

(x2 ∨ x3) ∧ ((x2 ∧ x3) → x4) = 1

 

… 

(x6 ∨ x7) ∧ ((x6 ∧ x7) → x8) = 1

(x7 ∨ x8) = 1

 

(x1 → y1) = 1 

(x2 → y2) = 1 

…

(x8 → y8) = 1

Построим дерево для x, в начале сформулировав правила для построения дерева:

x1 ∨ x2 = 1, следовательно, два нуля подряд идти не могут.

(x1 ∧ x2) → x3. Следовательно, если из единицы идет единица, то далее идут только единицы.

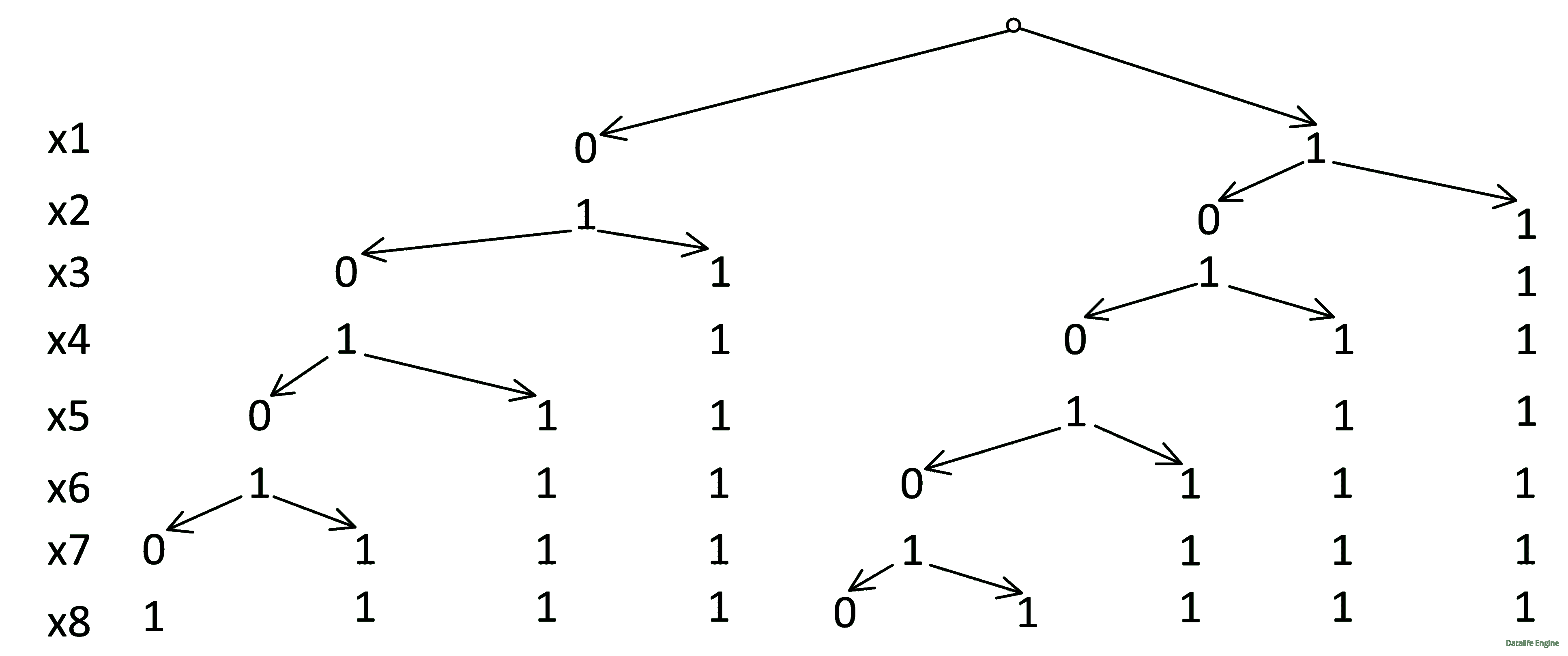
Посмотрим теперь на уравнения вида x → y = 0

В узлах х = 0 y принимает два значения,

в узлах х = 1 y принимает одно значение (y = 1).

Сделаем обсчет дерева (для удобства восприятия метка стоит только у удваивающихся узлов):

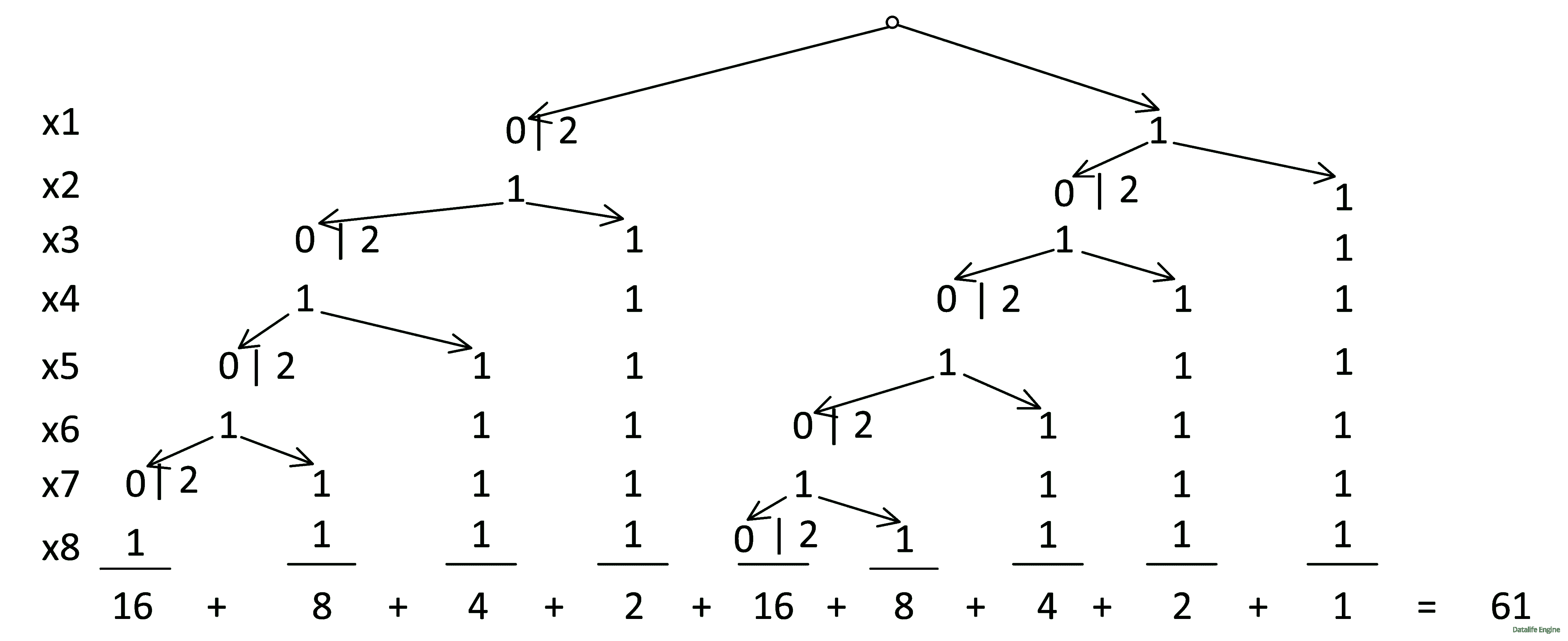
 Ответ: 61

Постройте два дерева – для x и y - и подумайте, как соединить ветки

Заметим, что ⌐y1 ∨ y2 = y1 → y2, поэтому система имеет вид:

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1

(x1 → y1) ∧ (x2 → y2) ∧ (x3 → y2) ∧ (x4 → y4) = 1

Переменные первого уравнения и второго связываются третьим, поэтому построим деревья для первого и второго уравнений и подумаем, как связать их ветви. Деревья одинаковы, и мы такое дерево уже построили в предыдущей задаче. Запишем их в табличном виде:

x1 0 0 0 0 1 x2 0 0 0 1 1 x3 0 0 1 1 1 x4 0 1 1 1 1

y1 0 0 0 0 1 y2 0 0 0 1 1 y3 0 0 1 1 1 y4 0 1 1 1 1

 

Свяжем ветви двух деревьев.

 

Ошибка. Некоторые считают, что ответ 5, и соединяют ветки таким образом:

x1	0	0	0	0	1
x2	0	0	0	1	1
x3	0	0	1	1	1
x4	0	1	1	1	1
y1	0	0	0	0	1
y2	0	0	0	1	1
y3	0	0	1	1	1
y4	0	1	1	1	1

Совсем не обязательно, чтобы первая ветка x соединялась бы только с первой веткой y.

Продолжение хода решения.

Посмотрим на первую ветку x.

x1	0
x2	0
x3	0
x4	0

Поскольку в ней одни нули, а из нуля может следовать что угодно, истина будет всегда. Посмотрим на третье уравнение:

(0 → y1) ∧ (0 → y2) ∧ (0 → y2) ∧ (0 → y4) = 1

Получается, что первая ветка x соединяется со всеми ветками y, что образует 5 решений.

Посмотрим на вторую ветку x:

x1	0
x2	0
x3	0
x4	1

(0 → y1) ∧ (0 → y2) ∧ (0 → y2) ∧ (1 → y4) = 1

Чтобы уравнение было истинным, нужно, чтобы y4 = 1

Вторая ветка x соединяется с 4 ветками y.

Аналогично третья ветка x соединяется с 3 ветками y.

И так далее:

Всего решений: 5 + 4 + 3 + 2 + 1 = 15

Ответ: 15

Разделите уравнения на части, а затем соедините эти части по-другому в три уравнения (иксы с иксами, игреки с игреками и третье уравнение - соединительное).

Поскольку уравнения представляют собой конъюнкцию (логическое умножение), каждый из «множителей» равен 1. Мы можем разделить уравнения:

(x1 → x2) = 1

(y1 → y2) = 1

(y1 → x1) = 1

 

(x2 → x3) = 1

(y2 → y3) = 1

(y2 → x2) = 1

…

(x8 → x9) = 1

(y8 → y9) = 1

(y8 → x8) = 1

(y9 → x9) = 1

Перегруппируем уравнения, разделим их на три группы:

(x1 → x2) = 1 (x2 → x3) = 1 … (x8 → x9) = 1

(y1 → y2) = 1 (y2 → y3) = 1 … (y8 → y9) = 1

(y1 → x1) = 1 (y2 → x2) = 1 … (y9 → x9) = 1

 

Соединим уравнения в три новых:

(x1 → x2) ∧ (x2 → x3) ∧ … ∧ (x8 → x9) = 1

(y1 → y2) ∧ (y2 → y3) ∧ … ∧ (y8 → y9) = 1

(y1 → x1) ∧ (y2 → x2) ∧ … ∧ (y9 → x9) = 1

 

Получилась система уравнений, как в предыдущей задаче, только с бОльшим числом переменных.

Количество решений: 10 + 9 + 8 + … + 1 = (10 + 1) * 10/2 = 55

Ответ: 55.

Аналогично предыдущей задаче, постройте три дерева. Присвойте имена веткам и соединяйте их с помощью дополнительного дерева.

Как и в предыдущей задаче, выпишем решения для уравнений x, y, z. Поскольку три ветки соединять, как мы это делали в предыдущей задаче, весьма затруднительно, присвоим веткам имена:

x1	0	0	0	0	0	0	1
x2	0	0	0	0	0	1	1
x3	0	0	0	0	1	1	1
x4	0	0	0	1	1	1	1
x5	0	0	1	1	1	1	1
x6	0	1	1	1	1	1	1
	A1	A2	A3	A4	A5	A6	A7

 

y1	0	0	0	0	0	0	1
y2	0	0	0	0	0	1	1
y3	0	0	0	0	1	1	1
y4	0	0	0	1	1	1	1
y5	0	0	1	1	1	1	1
y6	0	1	1	1	1	1	1
	B1	B2	B3	B4	B5	B6	B7

 

z1	0	0	0	0	0	0	1
z2	0	0	0	0	0	1	1
z3	0	0	0	0	1	1	1
z4	0	0	0	1	1	1	1
z5	0	0	1	1	1	1	1
z6	0	1	1	1	1	1	1
	C1	C2	C3	C4	C5	C6	C7

 

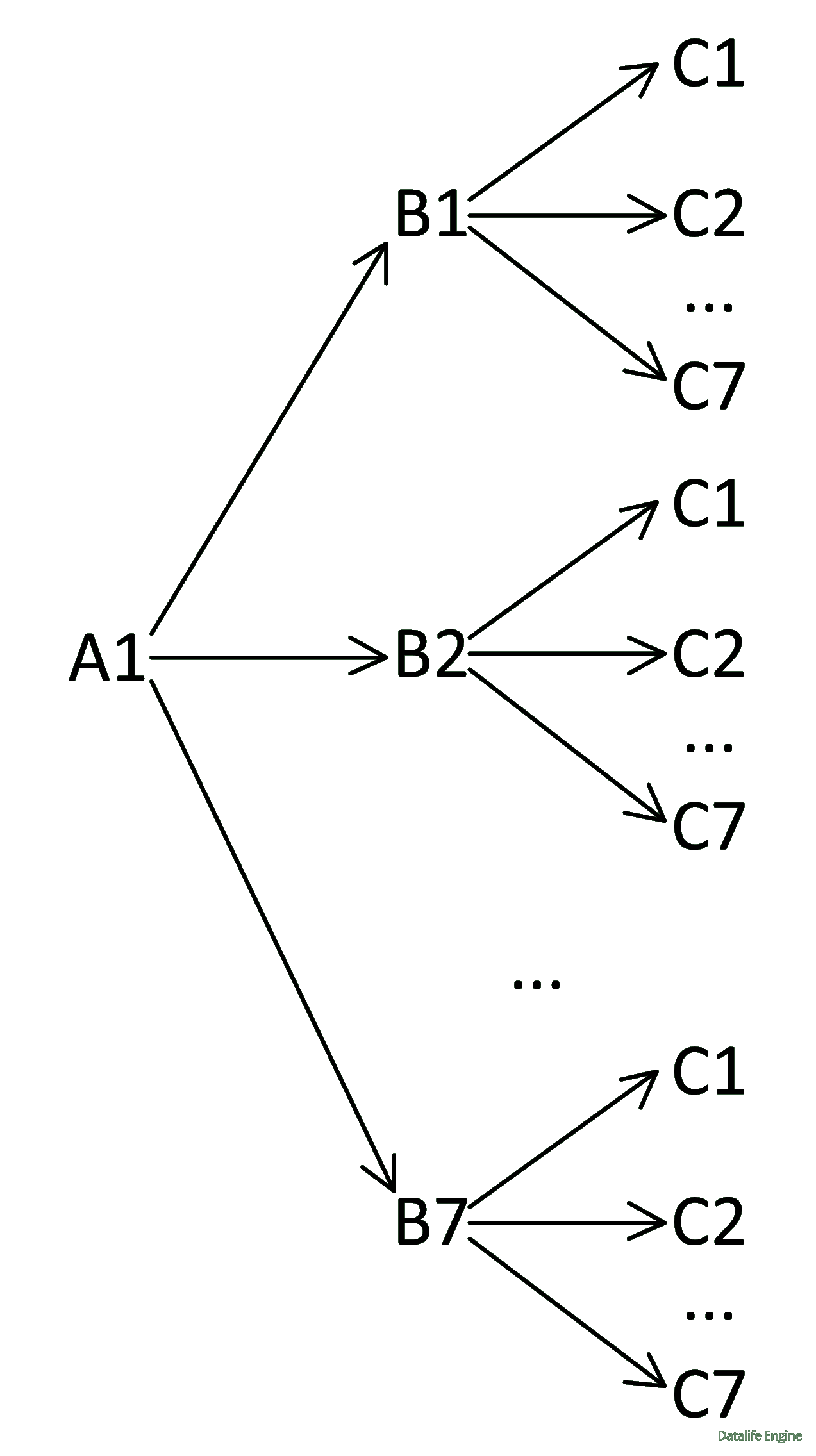
Построим дерево соединения веток по уравнению x6 ∧ y6 ∧ z6 = 0.

Заметим, что ветки соединяются по последней переменной и нам достаточно хотя бы одного нуля в последних переменных соединяемых веток.

 

Поскольку в ветке A1 последняя переменная x6 = 0, то она соединяется со всеми ветками B, а те, в свою очередь, со всеми С. Получаем 7 * 7 = 49 решений:

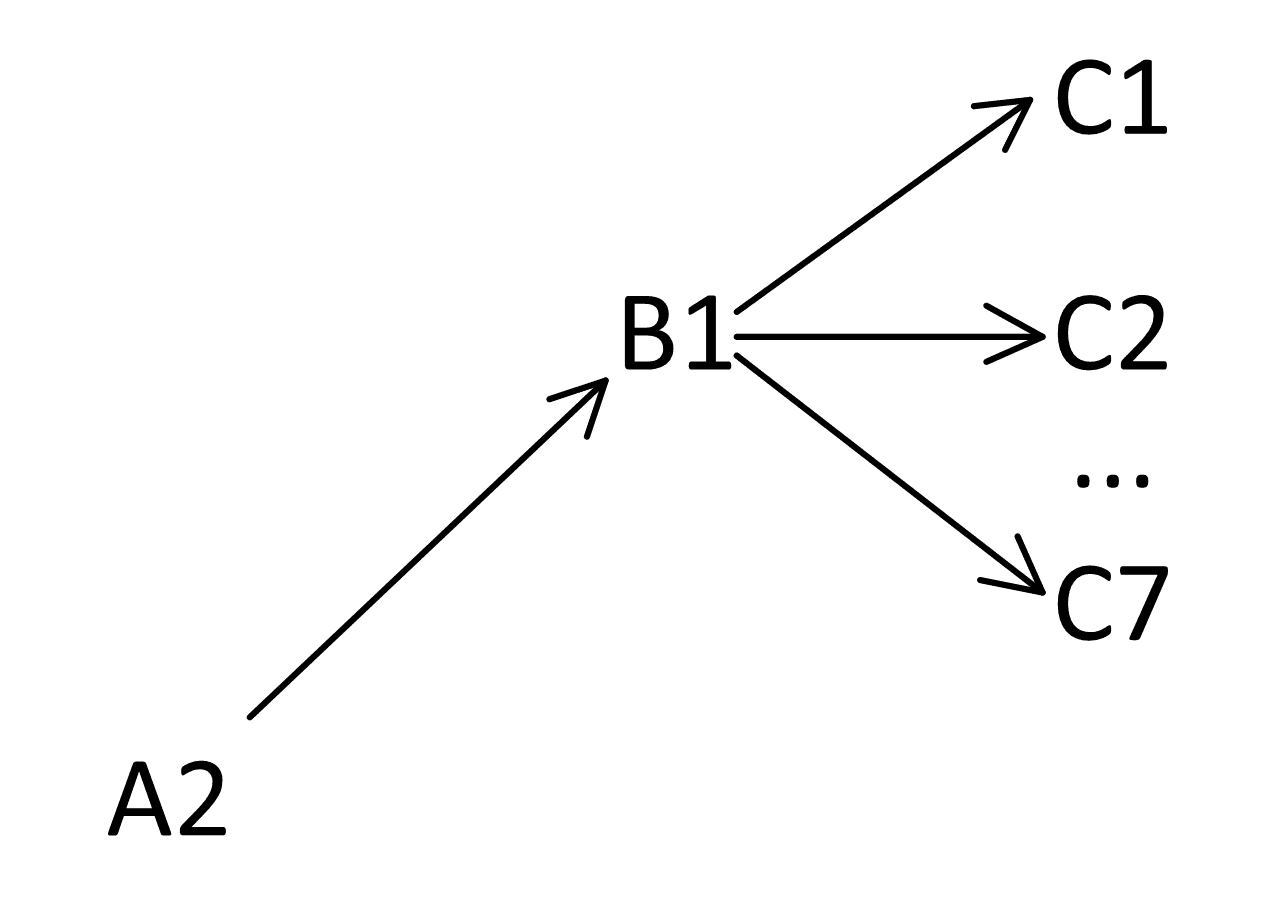
Рассмотрим ветку A2. В ней х6 = 1. Соединим её с B1. В ней y6 = 0, поэтому эта ветка соединяется со всеми С:

Соединим А2 с B2. В них х6 = 1 и y6 = 1. Поэтому z1 = 0. А это только одна ветка С1. И так А2 соединяется с B3 и т.д:

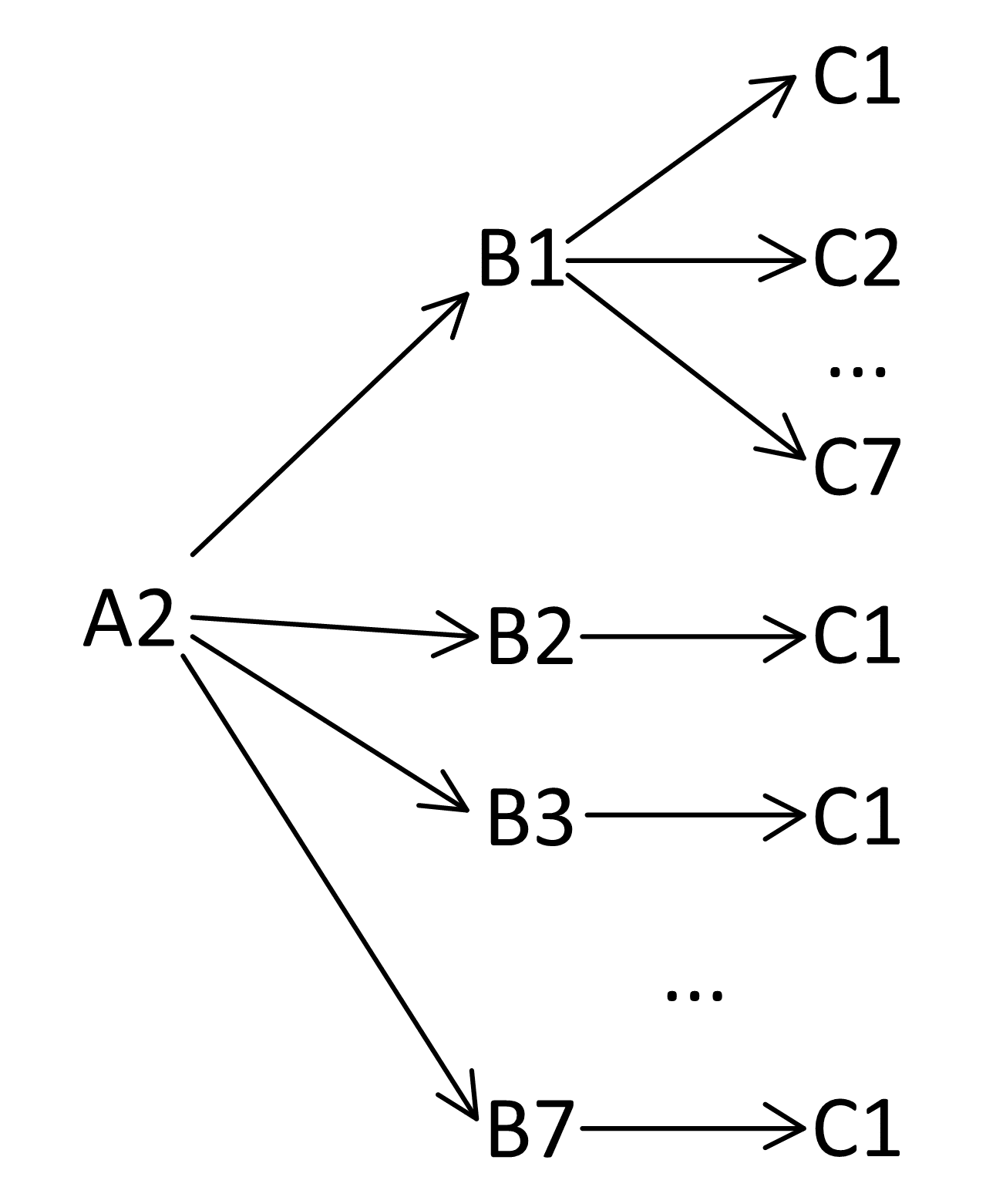
Для А2 всего 7 + 6 = 13 решений.

Столько же решений для А3…А7.

Всего 7 * 7 + (7 + 6) * 6 = 127 решений.

Ответ: 127

Предыдущие приемы: упрощение, введение новых обозначений, построение отдельного дерева - для x не пригодны. Вспомните задачи на теорию игр, когда шла игра сразу двумя кучами камней.

При построении дерева на одном уровне будем располагать x и y. Это означает, что в узле будут находиться две цифры, левая соответствует x, правая – y. Таким образом, ветки будут не двоиться, а учетверяться (если вы этого не понимаете, читайте комбинаторику – задачу 2.2.1):

(xy): (00), (01), (10), (11)

Выведем правила для построения дерева (сперва напишем все варианты, а потом будем вычеркивать лишнее):

Проанализируем (x1 ≡ y1) (x2 ≡ y2) = 1. Когда на первом уровне одинаковы x и y (это левая и правая ветки), то должны совпадать и x и y на втором уровне, иначе получится 1 → 0 = 0. Вычеркнем неправильные решения:

Проанализируем x1 → x2 = 1. Из нуля может следовать что угодно, из 1 – только 1:

Аналогично y1 → y2 = 1. Из нуля может следовать что угодно, из 1 – только 1:

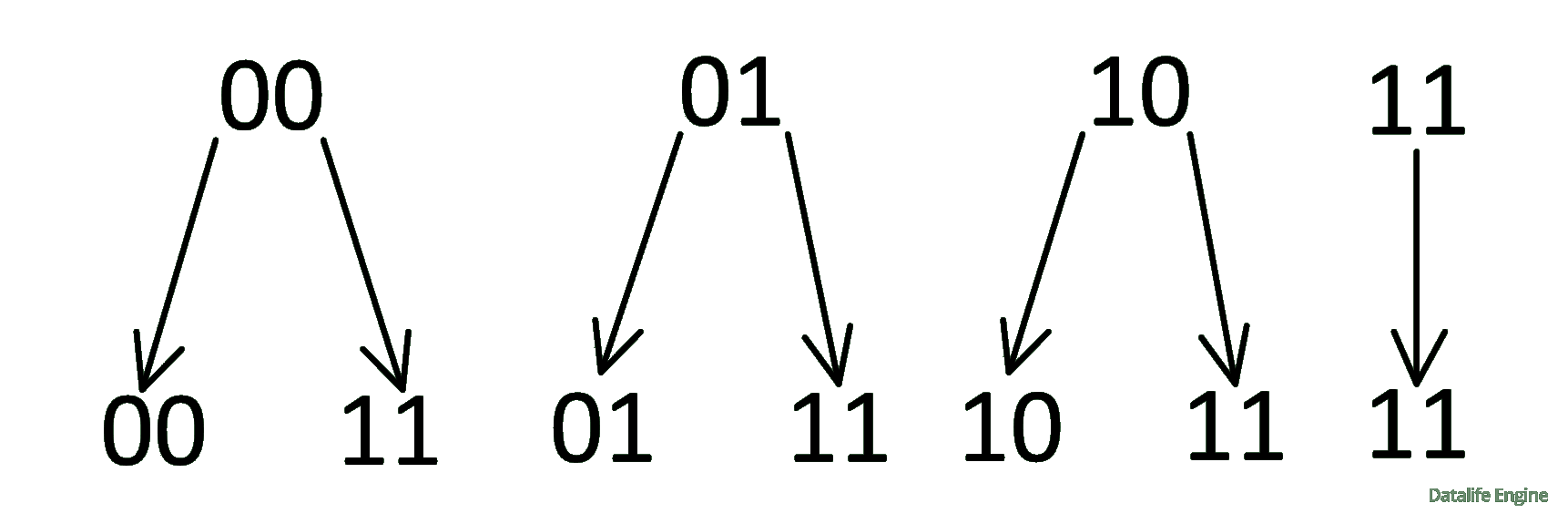
Итак, получаем правила построения дерева:

Построим по этим правилам дерево:

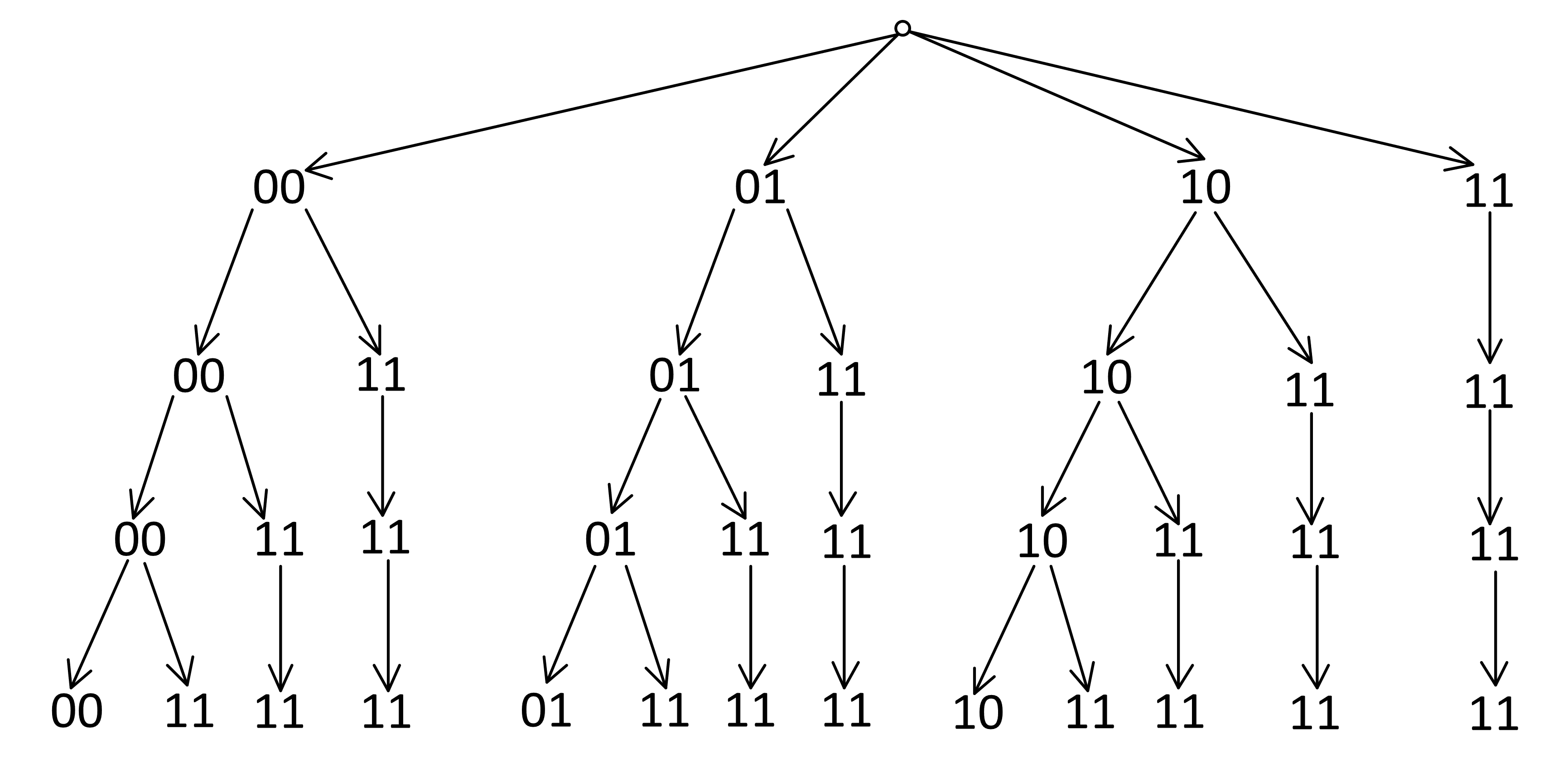
Видно, что крайняя правая ветка не ветвится, а остальные три ветки на каждом уровне увеличиваются на 1. Таким образом, на 9 уровне решений 3 * 9 + 1 = 28

Ответ: 28

Как и в предыдущей задаче, строится одно общее дерево сразу для двух переменных x и y. Подумайте, с какого индекса переменных удобнее начать строить дерево, в прямом порядке (1, 2, 3, 4, 5) или в обратном (5, 4, 3, 2, 1)?

Выберем обратный порядок индексов при построении дерева, так как при прямом порядке у нас сразу 4 варианта значений для x1 y1, а для x5 y5 мы ограничены тремя вариантами (0 ∨ 0 = 0):

В предпоследнем уравнении не должно быть полного совпадения пар переменных x5 y5 и x4 y4. Все остальные варианты возможны:

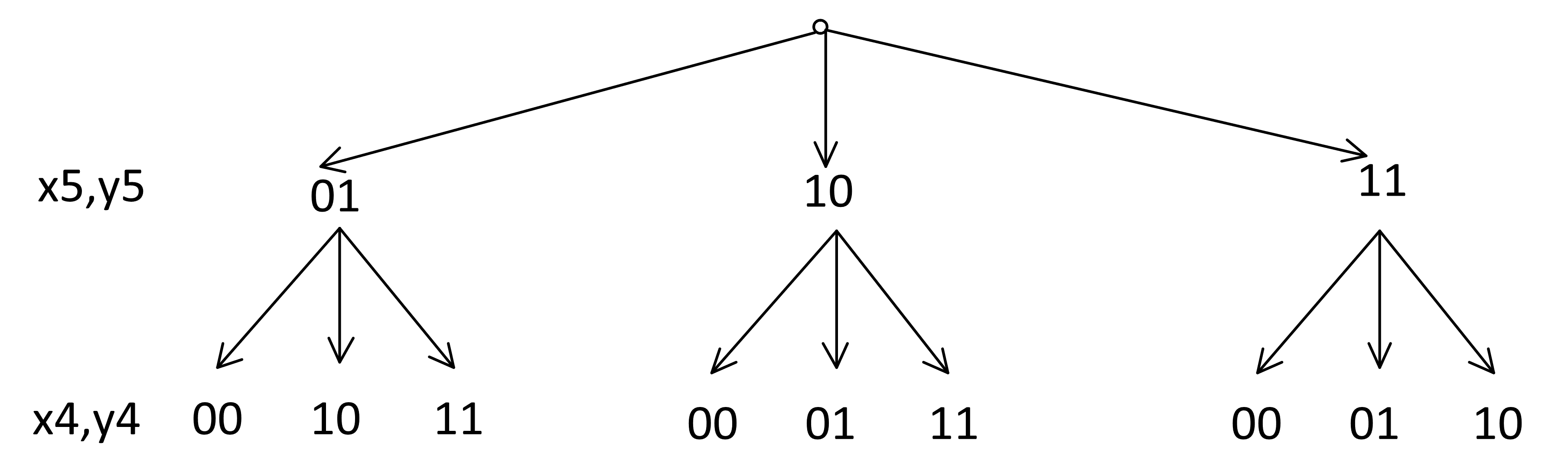
Аналогично дальше каждый узел ветвится на три узла:

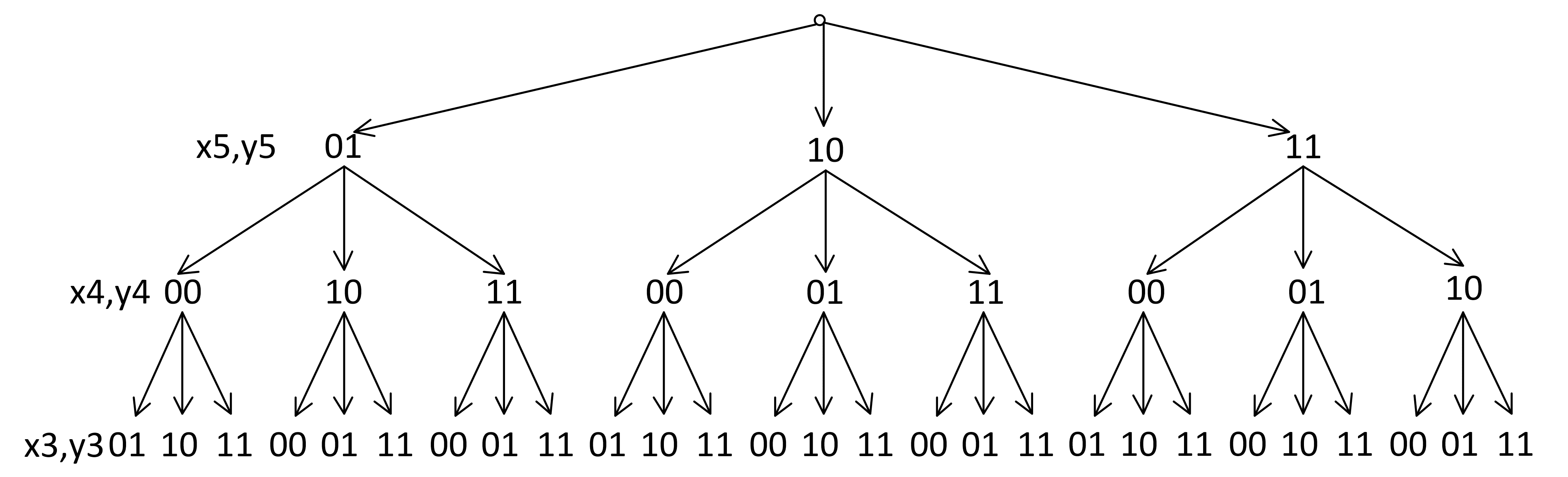
С учетом того, что у нас пять уравнений, общее количество решений равно 3 * 3 * 3 * 3 * 3 = 243.

Примечание. При построении дерева в прямом порядке дерево сперва ветвится на 4 части, затем на три: 4 * 3 * 3 * 3. На последнем уровне нам не подходит вариант 00, но вот в каких именно ветках он встречается – непонятно, так как веток очень много. Поэтому прямой порядок не годится.

Ответ: 243.

 Стройте дерево, на каждом уровне которого будет по две переменных.

Новые обозначения ввести не получится. Хотя переменные образуют устойчивые группы, но в левых скобках – конъюнкция, а в правых – дизъюнкция.

Построим дерево, в котором на каждом из уровней будет по два икса (возможно построение и обычного дерева, но это неудобно и требует внимательности).

Начнем строить дерево. На первом уровне будет четыре варианта всех значений x1 и x2:

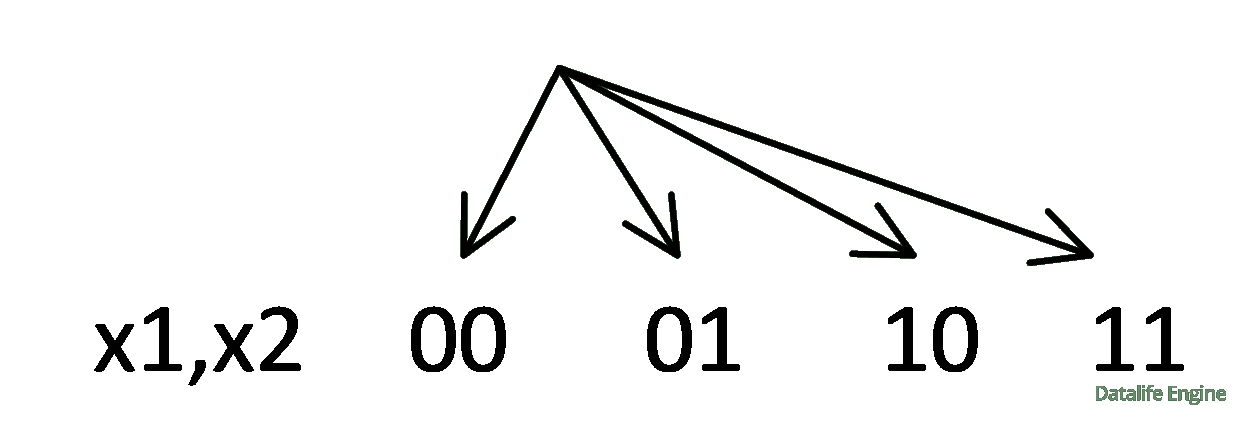
Рассмотрим ветку 00:

(0 ∨ 0) → (x3 ∧ x4) = 1

0 → (x3 ∧ x4) = 1

Импликация 0 → ? = 1 при любых значениях второго аргумента, то есть при любых значениях x3 и x4. Следовательно, ветка 00 порождает четыре ветки:

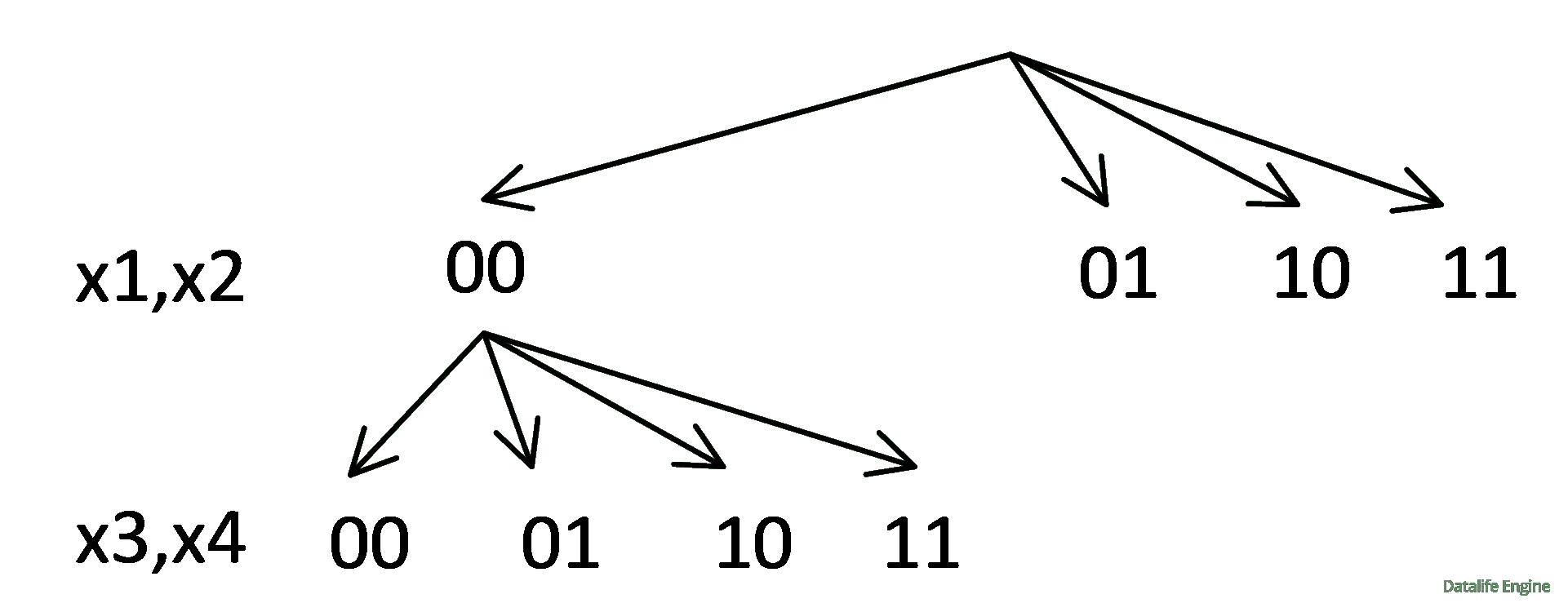
Рассмотрим ветки 01, 10, 11:

(0 ∨ 1) → (x3 ∧ x4) = 1

(1 ∨ 0) → (x3 ∧ x4) = 1

(1 ∨ 1) → (x3 ∧ x4) = 1

Для всех них:

1 → (x3 ∧ x4) = 1

Импликация из 1 равна единице только в одном случае:

1 → 1 = 1

Следовательно,

x3 ∧ x4 = 1

Это возможно только в одном случае: x3 = 1, x4 = 1:

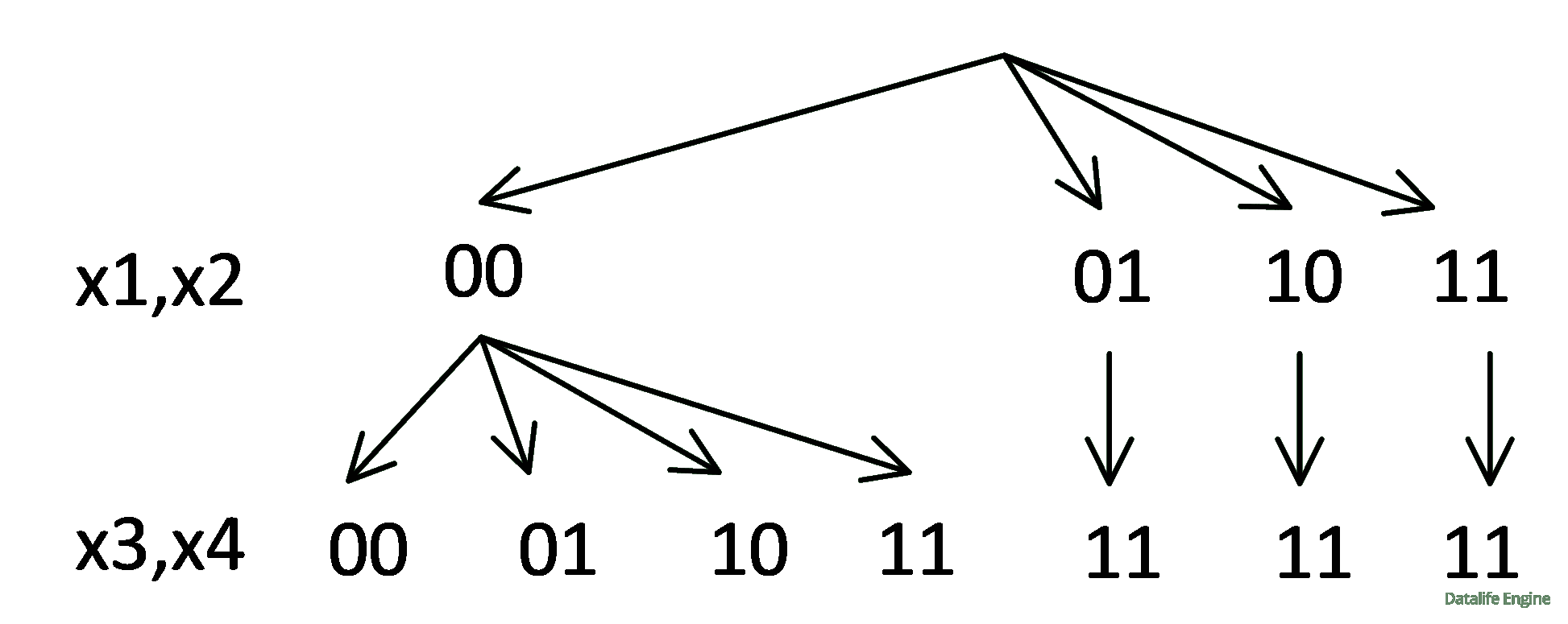
Дальше дерево пойдет точно так же. Ветка 00 будет порождать четыре ветки, а остальные превращаться в 11:

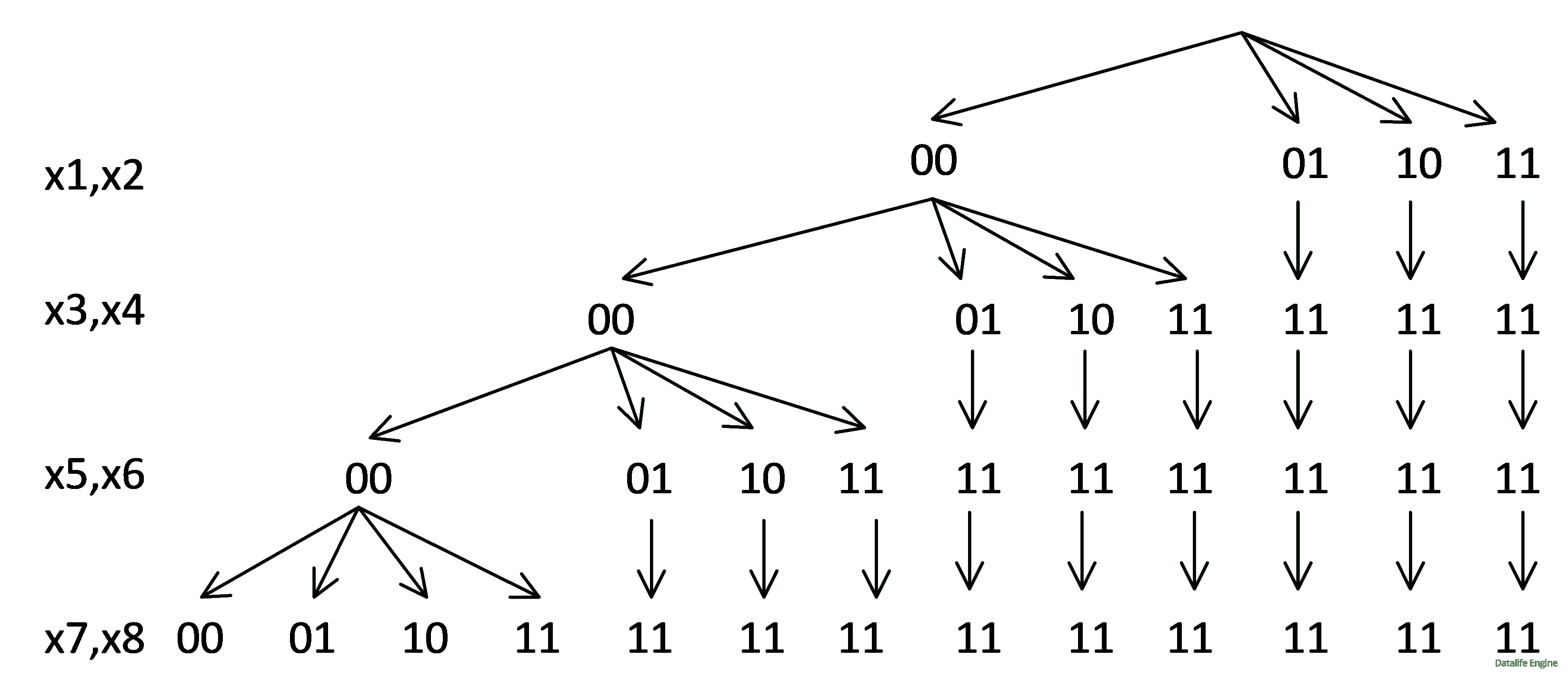
Количество веток соответствует количеству решений.

Ответ: 13

Введите новые обозначения. Постройте дерево  решений для левых множителей. При возврате к исходным обозначениям учтите правые множители, исключив неподходящие решения.

Из предыдущих задач может сложиться впечатление, что эту задачу нужно решать тетрарным деревом (две переменных на одном уровне), но это не так.

Поскольку каждое уравнение представляет собой логическое «и» (логическое умножение), то каждый из множителей равен 1. Мы можем разъединить уравнения:

((x1 ∨ y1) → (x2 ∨ y2)) = 1

((x2 ∨ y2) → (x3 ∨ y3)) = 1

...

((x6 ∨ y6) → (x7 ∨ y7)) = 1

(x1 → y1) = 1

(x2 → y2) = 1

...

(x6 → y6) = 1

Рассмотрим верхние уравнения. Введем новые обозначения t1 = x1 ∨ y1…

Построим дерево решений для переменных t. Это уже знакомое нам дерево:

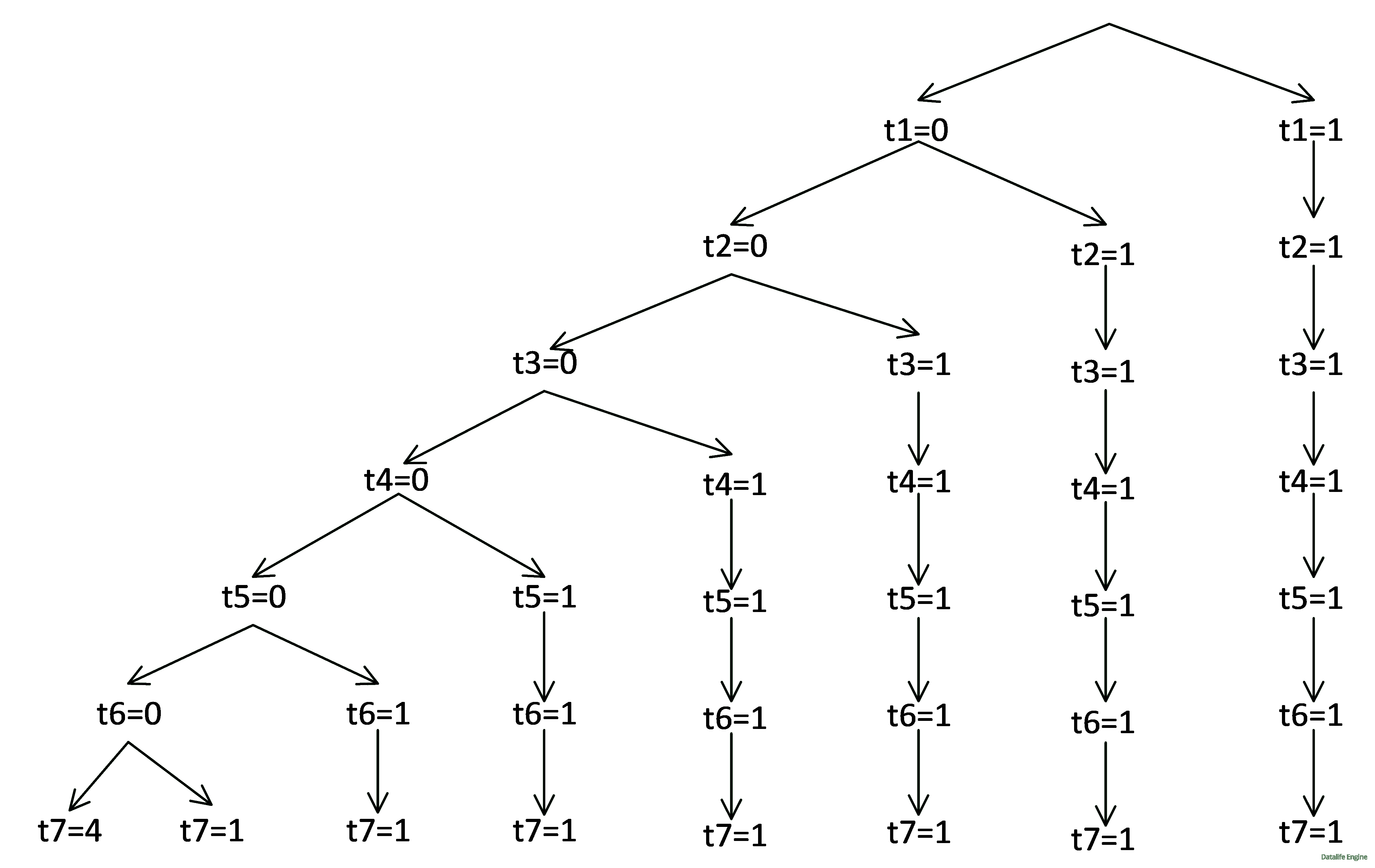
Вернемся к исходным обозначениям. В узлах t = 0

x ∨ y = 0 только в одном случае: при x = 0 и y = 0. Проверим при этих значениях нижнюю часть системы уравнений: (x → y) = 1

(0 → 0) = 1. Равенство выполняется, поэтому в нулевых узлах только одно решение:

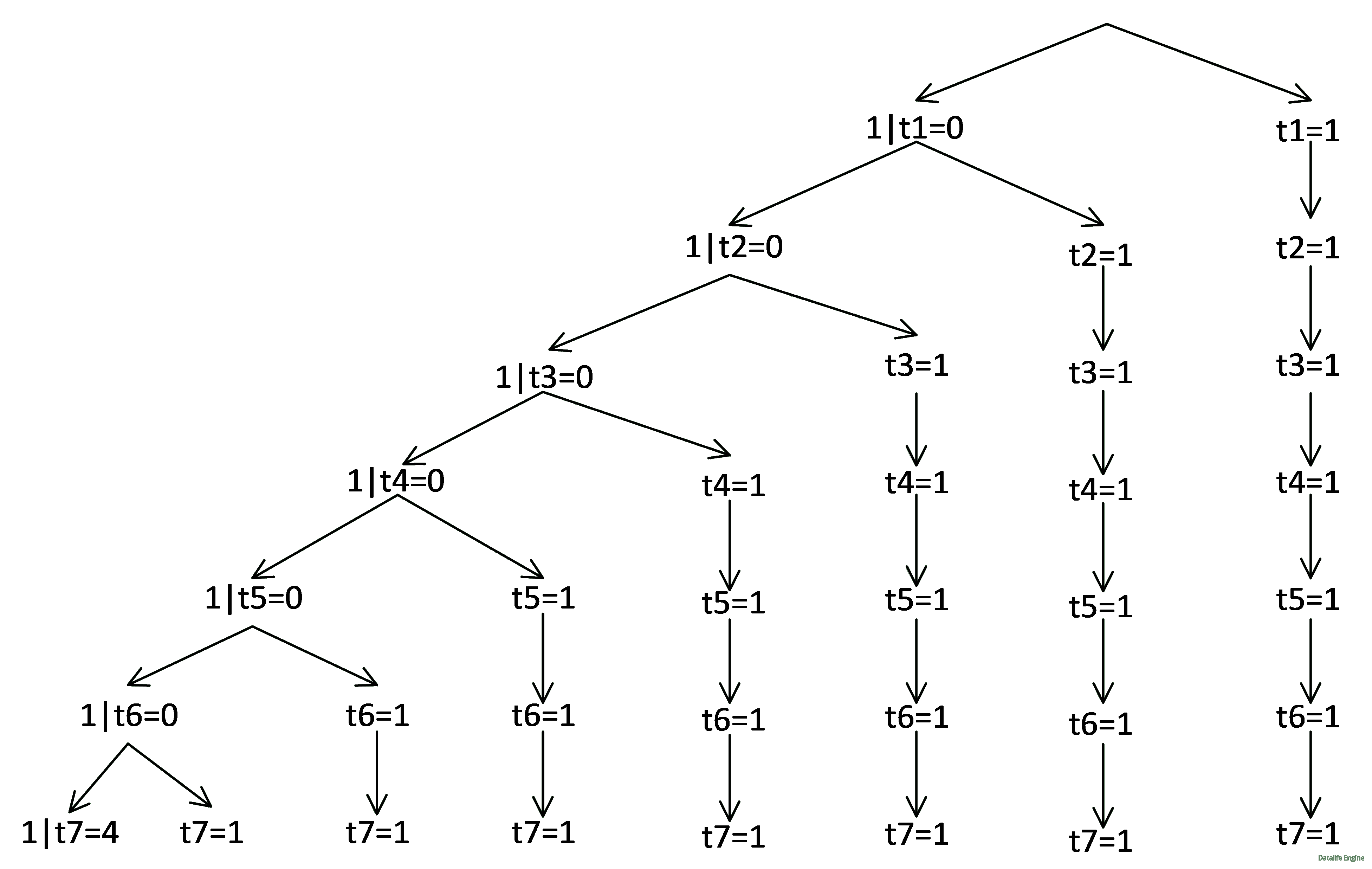
Рассмотрим узлы t = 1:

x ∨ y = 1 в трёх случаях:

1. x = 0, y = 1
2. x = 1, y = 0
3. x = 1, y = 1

Проверим уравнение (x → y) = 1

1. x = 0, y = 1, (0 → 1) = 1
2. x = 1, y = 0, (1 → 0) = 0
3. x = 1, y = 1, (1 → 1) = 1

Случай (1 → 0) = 0 исключается, следовательно, в узлах t = 1 два решения:

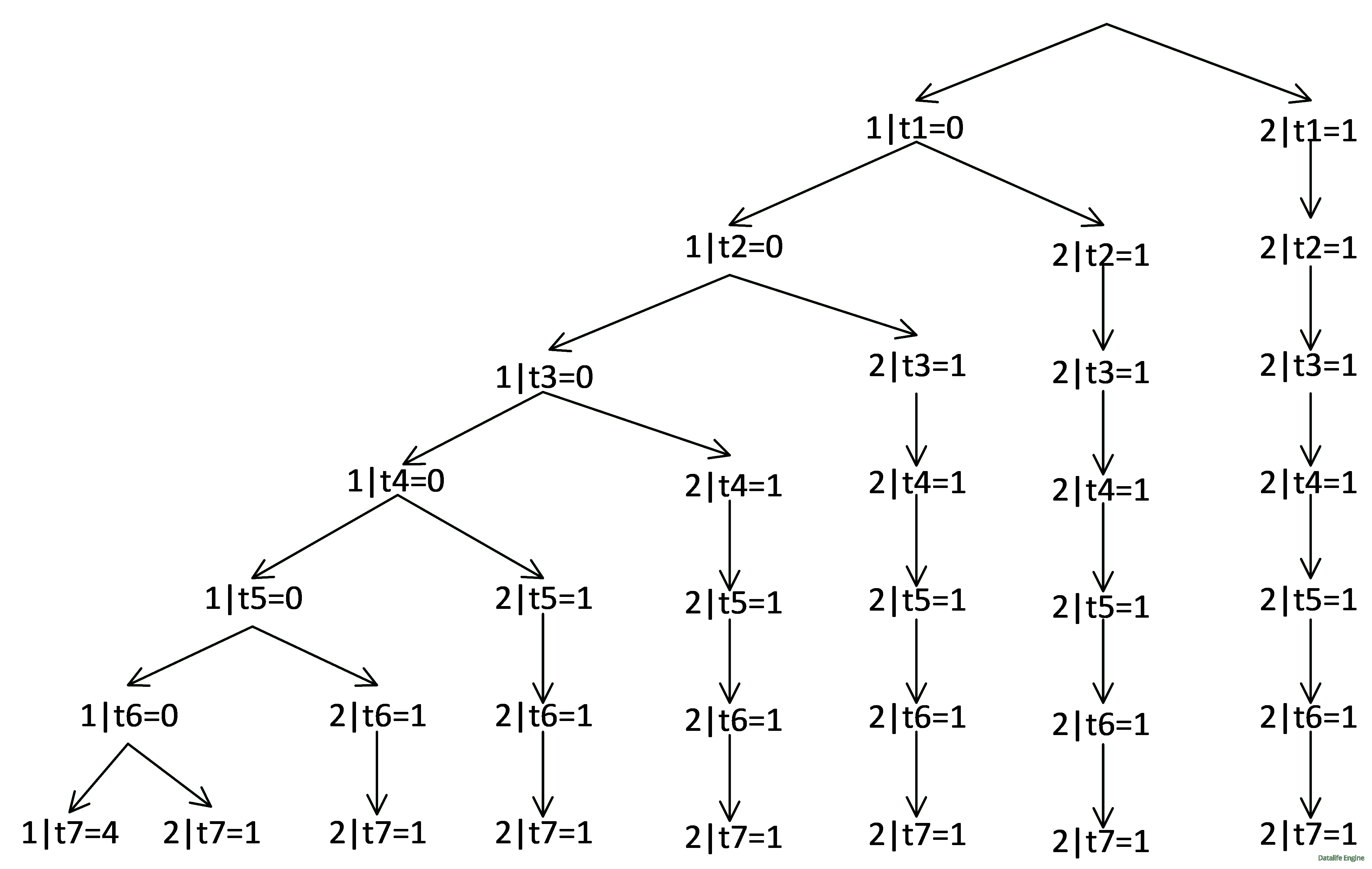
Произведем подсчет путем перемножения количества решений в узлах по каждой ветке и сложения результатов:

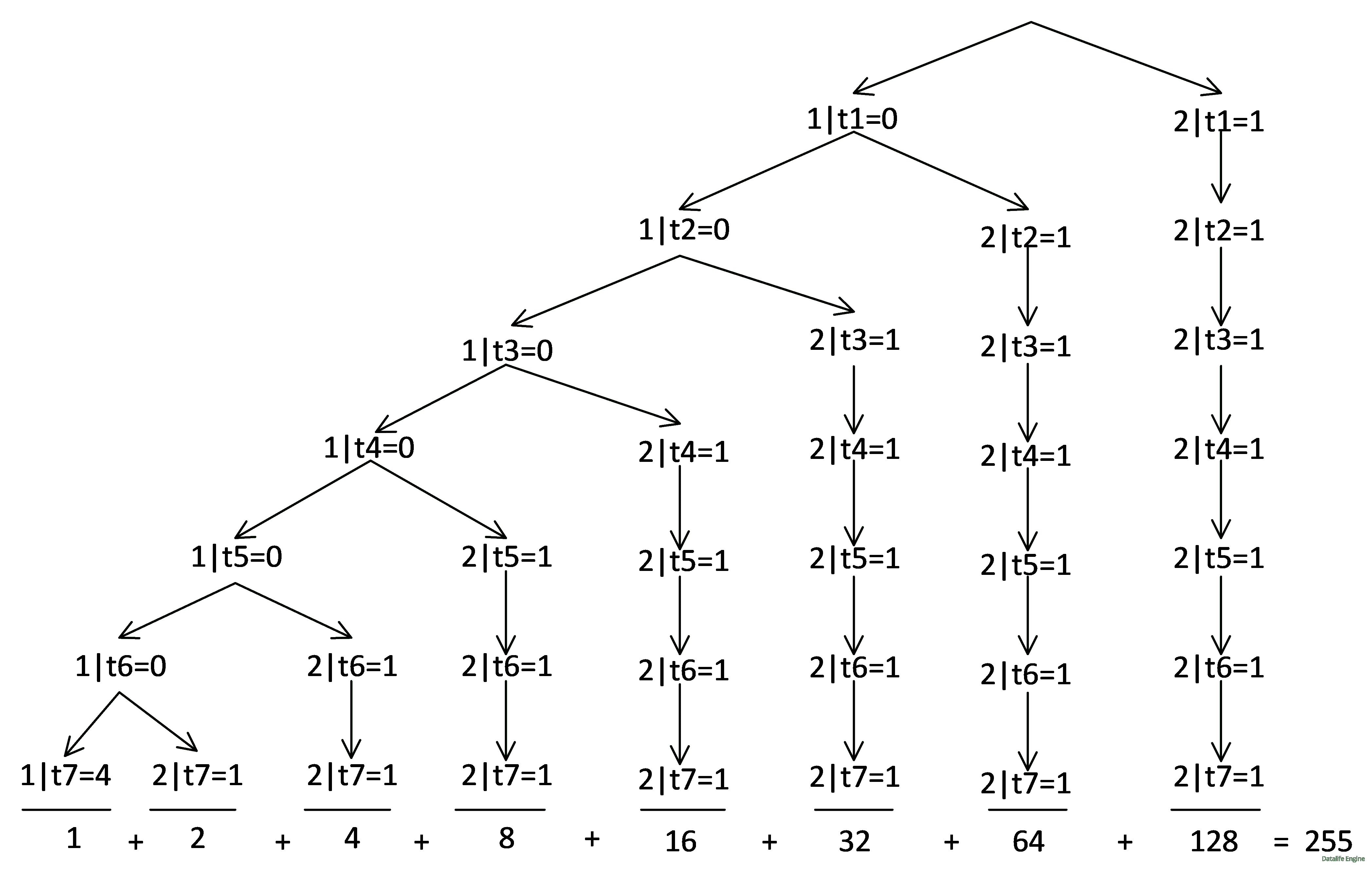
Ответ: 255

Прежде чем строить дерево (для данной системы это очень кропотливое занятие), постройте таблицу истинности для трех переменных.

Преобразуем уравнения:

(¬x1 ∧ x2 ∧ ¬x3) ∨ (¬x1 ∧ x2 ∧ x3) ∨ (x1 ∧ ¬x2 ∧ ¬x3) = 0,

(¬x2 ∧ x3 ∧ ¬x4) ∨ (¬x2 ∧ x3 ∧ x4) ∨ (x2 ∧ ¬x3 ∧ ¬x4) = 0,

...

(¬x8 ∧ x9 ∧ ¬x10) ∨ (¬x8 ∧ x9 ∧ x10) ∨ (x8 ∧ ¬x9 ∧ ¬x10) = 0.

Каждое из «слагаемых» в логическом «или» должно быть равно 0. 

«Слагаемые» представляют собой множители, соединенные логическим «и». Они принимают значение 1 только в одном случае:

¬x1 ∧ x2 ∧ ¬x3 = 1 при 010

¬x1 ∧ x2 ∧ x3 = 1 при 011

x1 ∧ ¬x2 ∧ ¬x3 = 1 при 100

Таким образом можно быстро заполнить таблицу истинности:

x1	x2	x3	уравнение
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	1	0	0
1	0	1	0
1	1	1	0

 

Нас устраивают строчки со значением выражения 0:

x1	x2	x3	уравнение
0	0	0	0
0	0	1	0
1	0	1	0
1	1	0	0
1	1	1	0

По таблице можно составить дерево:

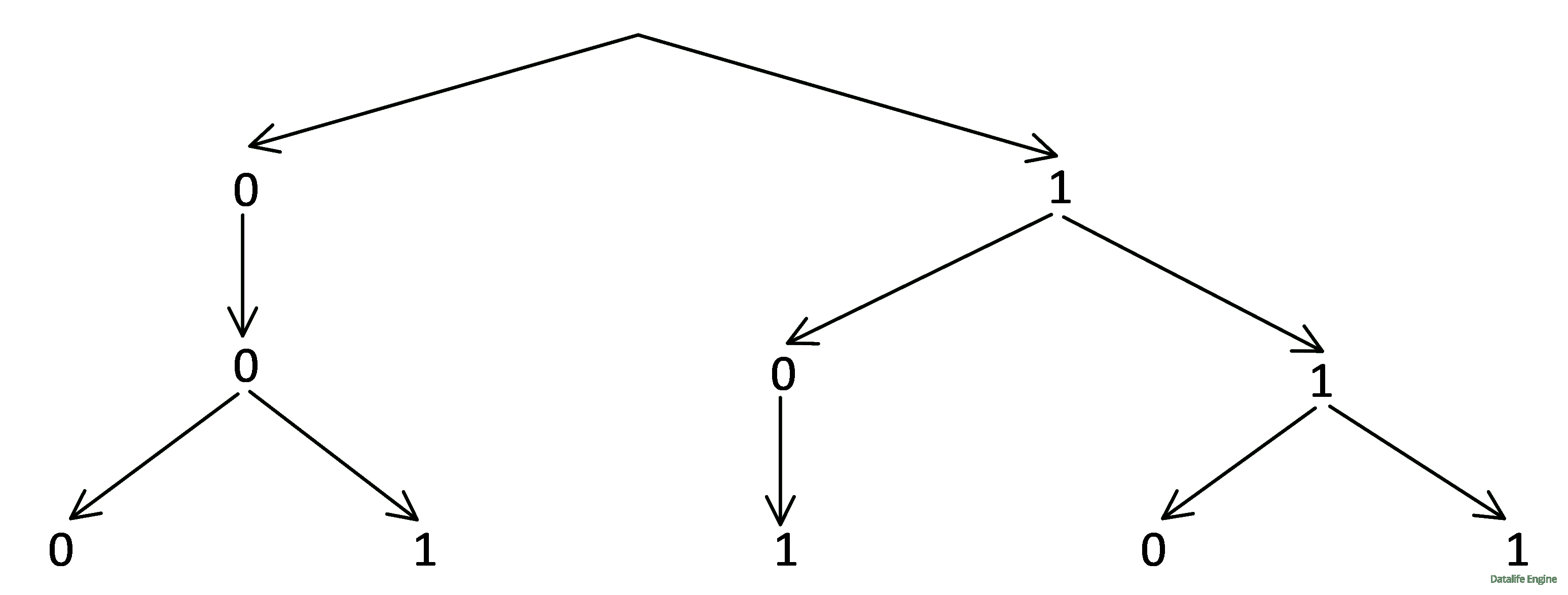
Составим таблицу для x2, x3, x4 (фактически возьмем таблицу для x1, x2, x3 и переименуем индексы):

x2	x3	x4	уравнение
0	0	0	0
0	0	1	0
1	1	0	0
1	0	1	0
1	1	1	0

 

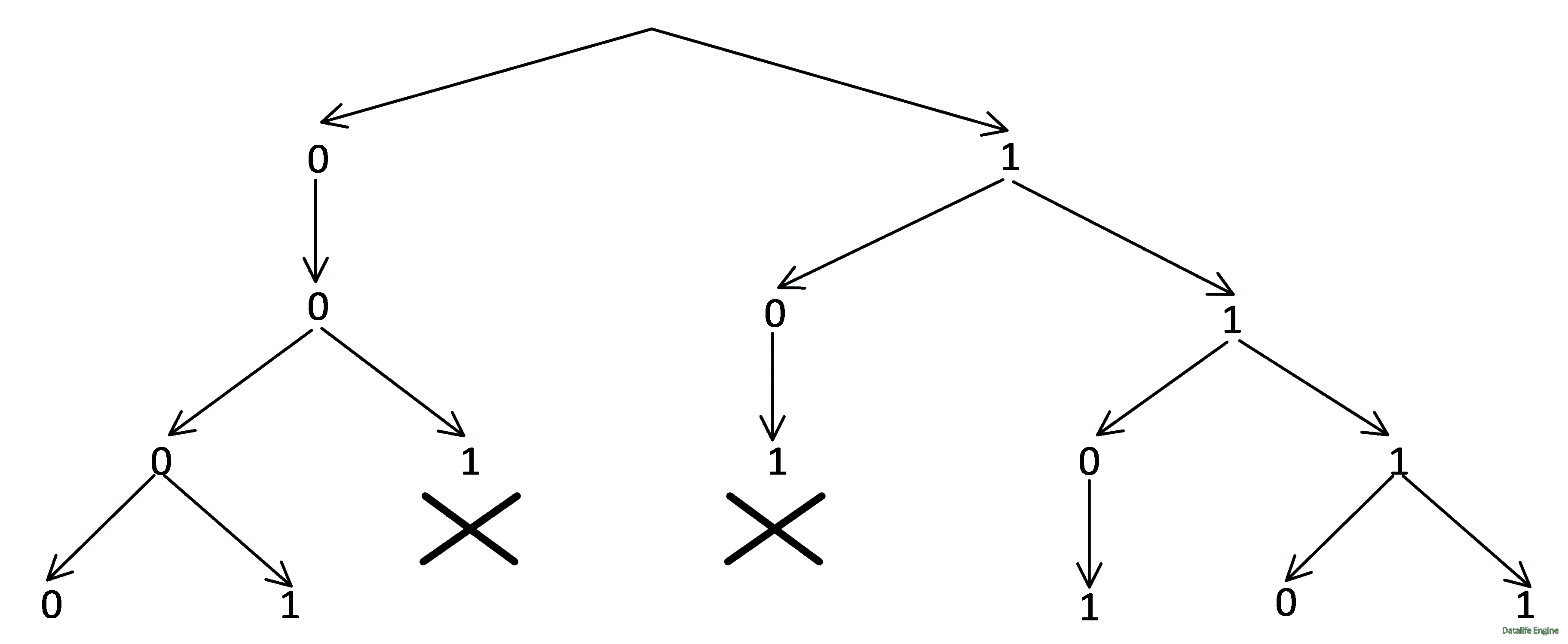
Попытаемся соединить две таблицы вместе, получив одну таблицу для x1, x2, x3, x4:

Мы увидим, что две строчки таблицы x1, x2, x3 не соединяются с таблицей x2, x3, x4:

001 

101

(мертвые ветки)

 

x1	x2	x3	x4
0	0	0	0
0	0	0	1
1	1	0	1
1	1	1	0
1	1	1	1

 

Аналогично соединению таблиц мы могли бы построить дерево:

Продолжаем дальше для таблицы x3, x4, x5

x2	x3	x4
0	0	0
0	0	1
1	1	0
1	0	1
1	1	1

 

При соединении «умирают» ветки x1, x2, x3, x4:

0001

1101

 

Таблица x1, x2, x3, x4, x5:

x1	x2	x3	x4	X5
0	0	0	0	0
0	0	0	0	1
1	1	1	0	1
1	1	1	1	0
1	1	1	1	1

 

Аналогично соединению таблиц мы могли бы продолжить строить дерево:

Сравним последние две колонки таблиц

x1, x2, x3

x1, x2, x3, x4

x1, x2, x3, x4, x5

И увидим, что они в точности одинаковые, несмотря на то, что мы соединяли таблицы и веточки «умирали». Это означает, что дальше соединение так и будет продолжаться. На 9 уровне будем иметь всё те же 5 решений.

Ответ: 5

Первое желание – это построить дерево для x, а затем для каждого узла посчитать количество y. Если не принимать во внимание y, то по таблице истинности для логического «и» получится система уравнений:

(x1 ∨ x2) = 1

(x2 ∨ x3) = 1

…

(x6 ∨ x7) = 1

(x7 ∨ x8) = 1

 

Начнем строить для неё дерево:

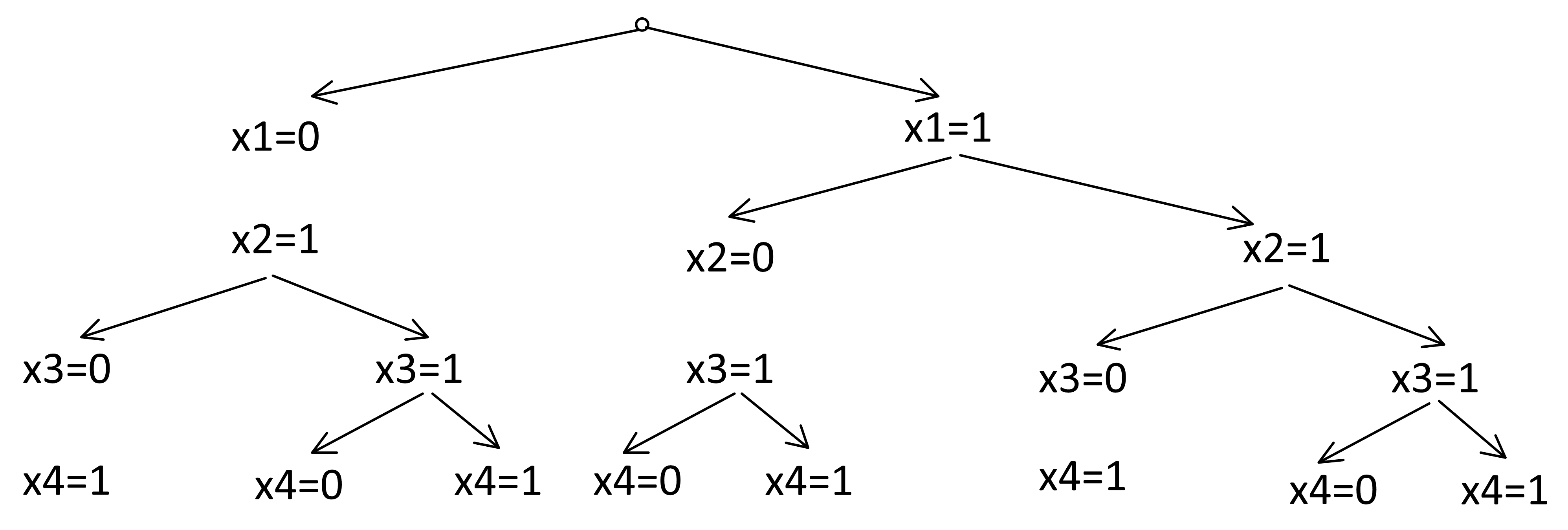
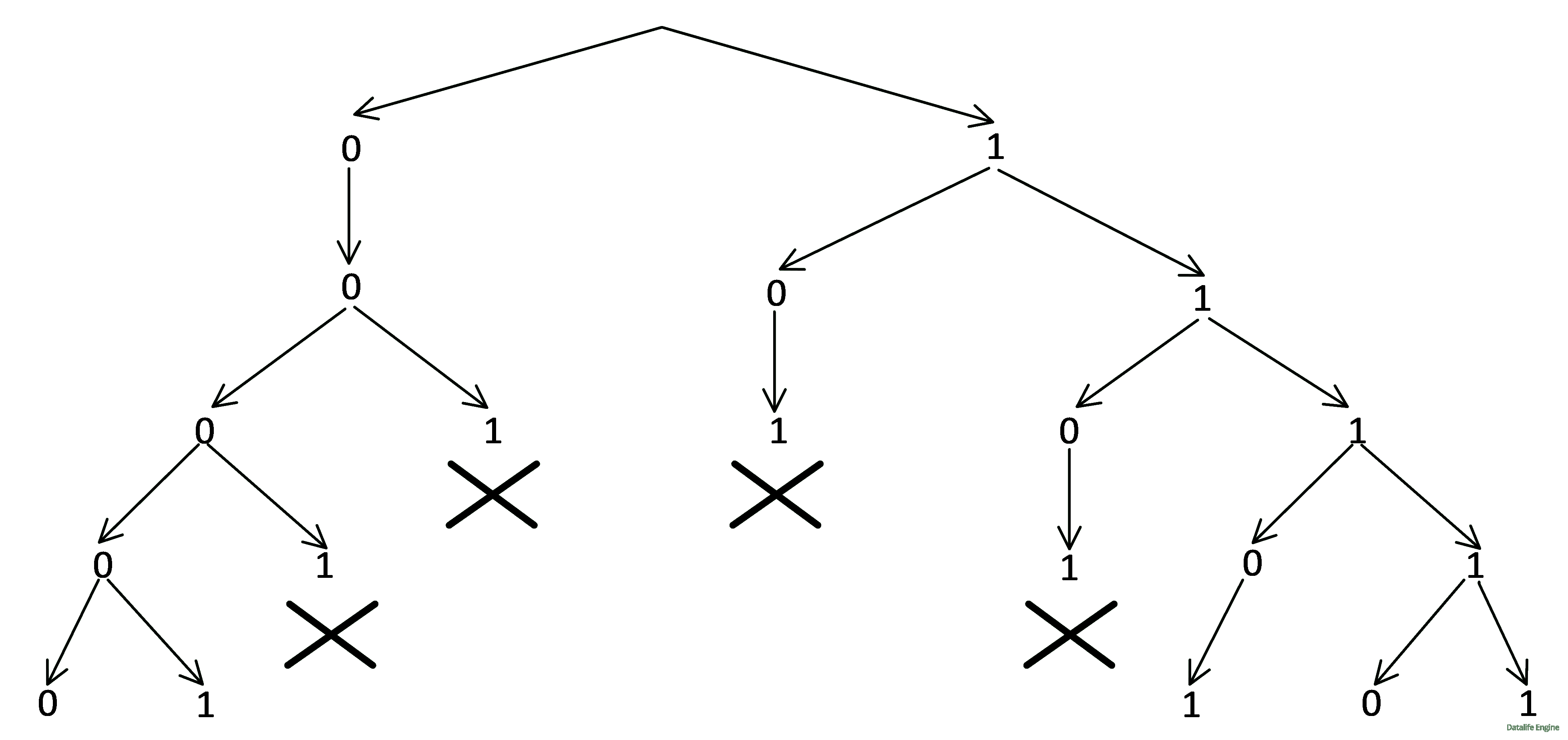
Видно, что дерево быстро ветвится (похоже, что по последовательности чисел Фибоначчи). Но даже если мы можем посчитать количество ветвей (оно равно 55), то непонятно, как посчитать количество y в каждом узле, чтобы посчитать общее количество решений.

Пока лишь оценим узлы, в которых происходит удвоение за счет двух решений y. Удвоение происходит тогда, когда соседние x не принимают одновременно значений 1:

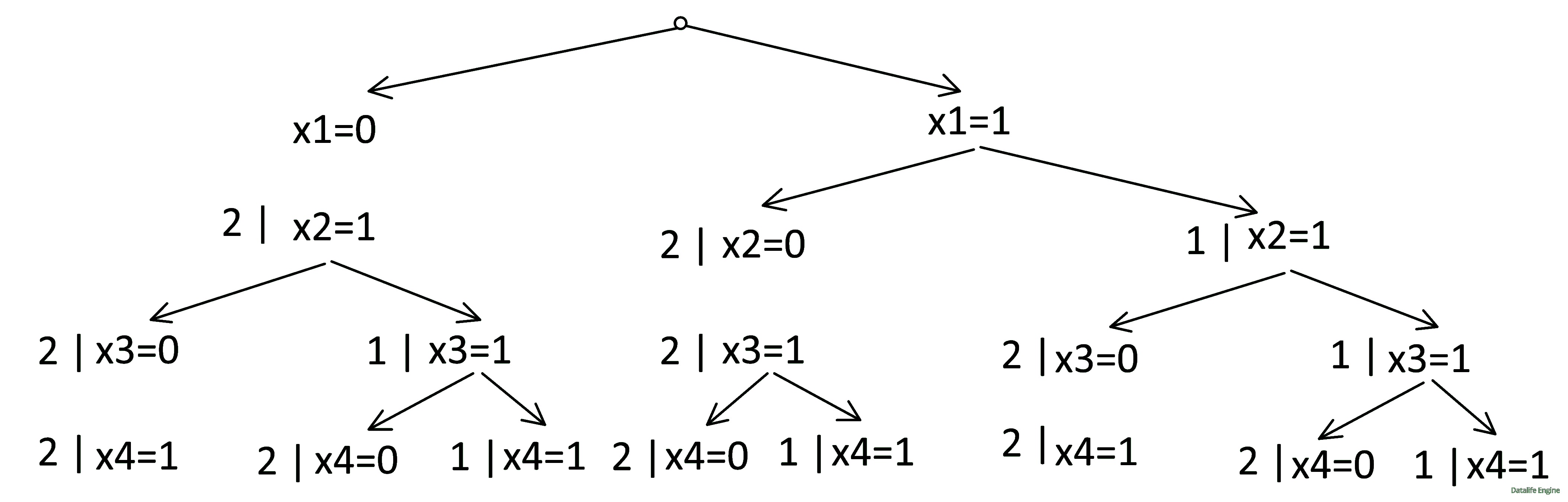
Воспользуемся методом подсчета из задачи 4.5.8. Будем не строить дерево, а на каждом уровне будем подсчитывать количество узлов разного вида. В дереве ошибочного решения есть три вида узлов: «0 удваивающийся неветвящийся», «1 после 0 удваивающаяся ветвящаяся», «1 после 1 неудваивающаяся ветвящаяся», и есть еще один дополнительный узел на первом уровне – «0 неудваивающийся».

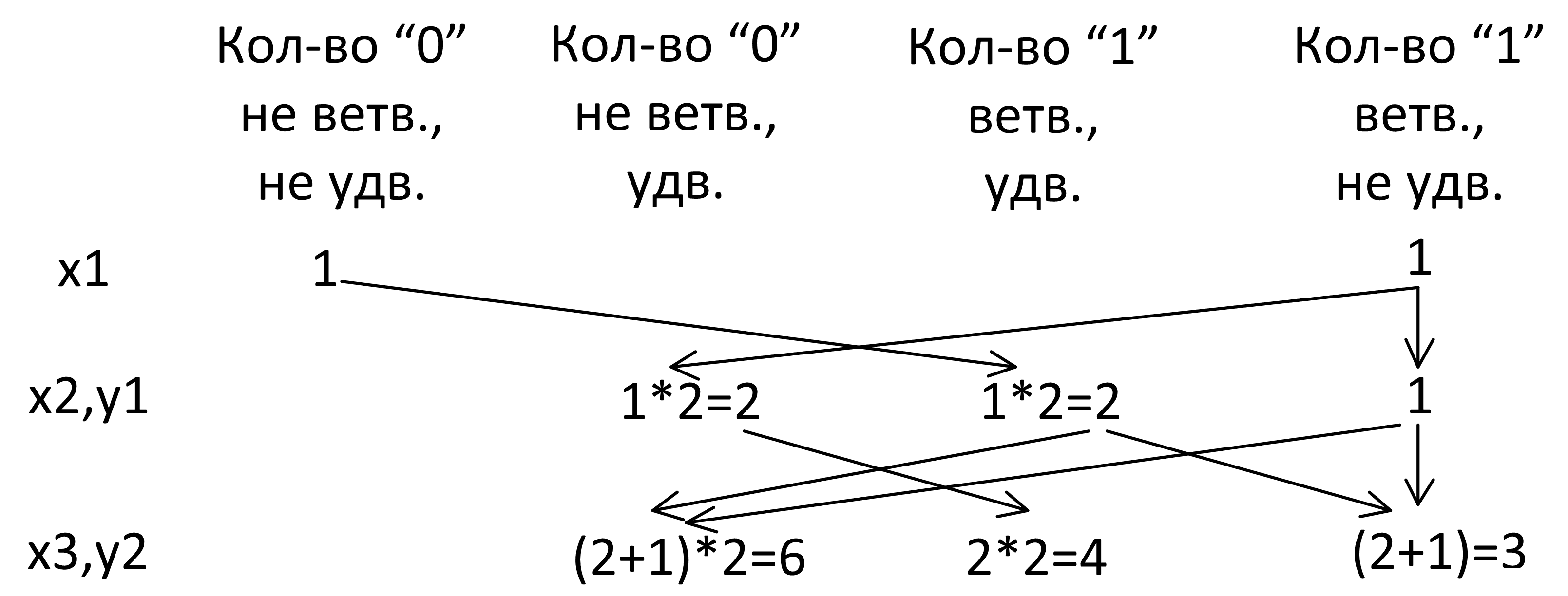
Продолжим вычислять сходным образом до тех пор, пока у нас идут однотипные уравнения, то есть до уровня x7 y6:

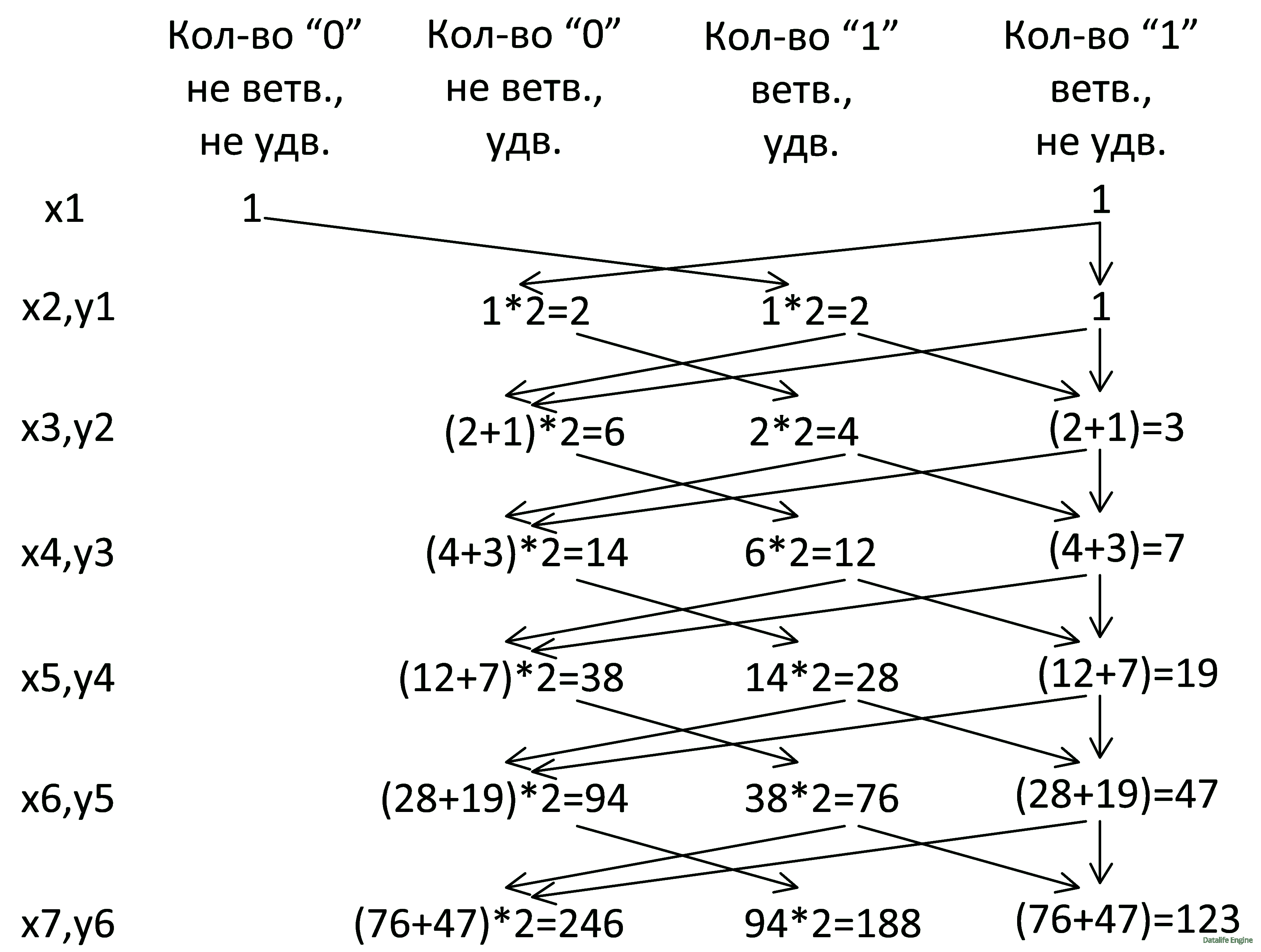
Далее поведение уравнений меняется, поэтому будем добавлять x8 и y7 не одновременно, а постепенно. То есть сперва добавим x8:

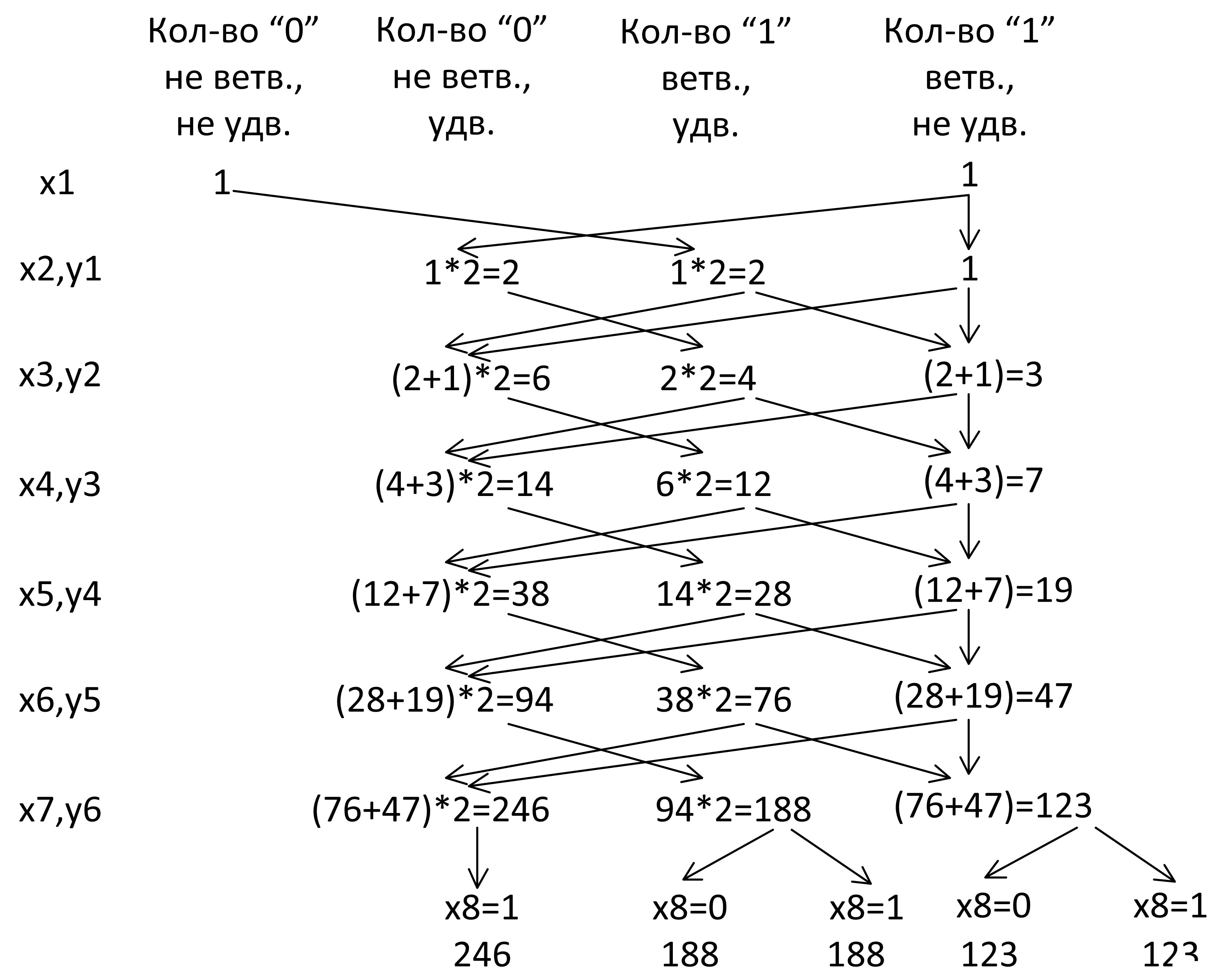
Добавим y7 и продолжим строить схему так, как будто это обычное дерево решений:

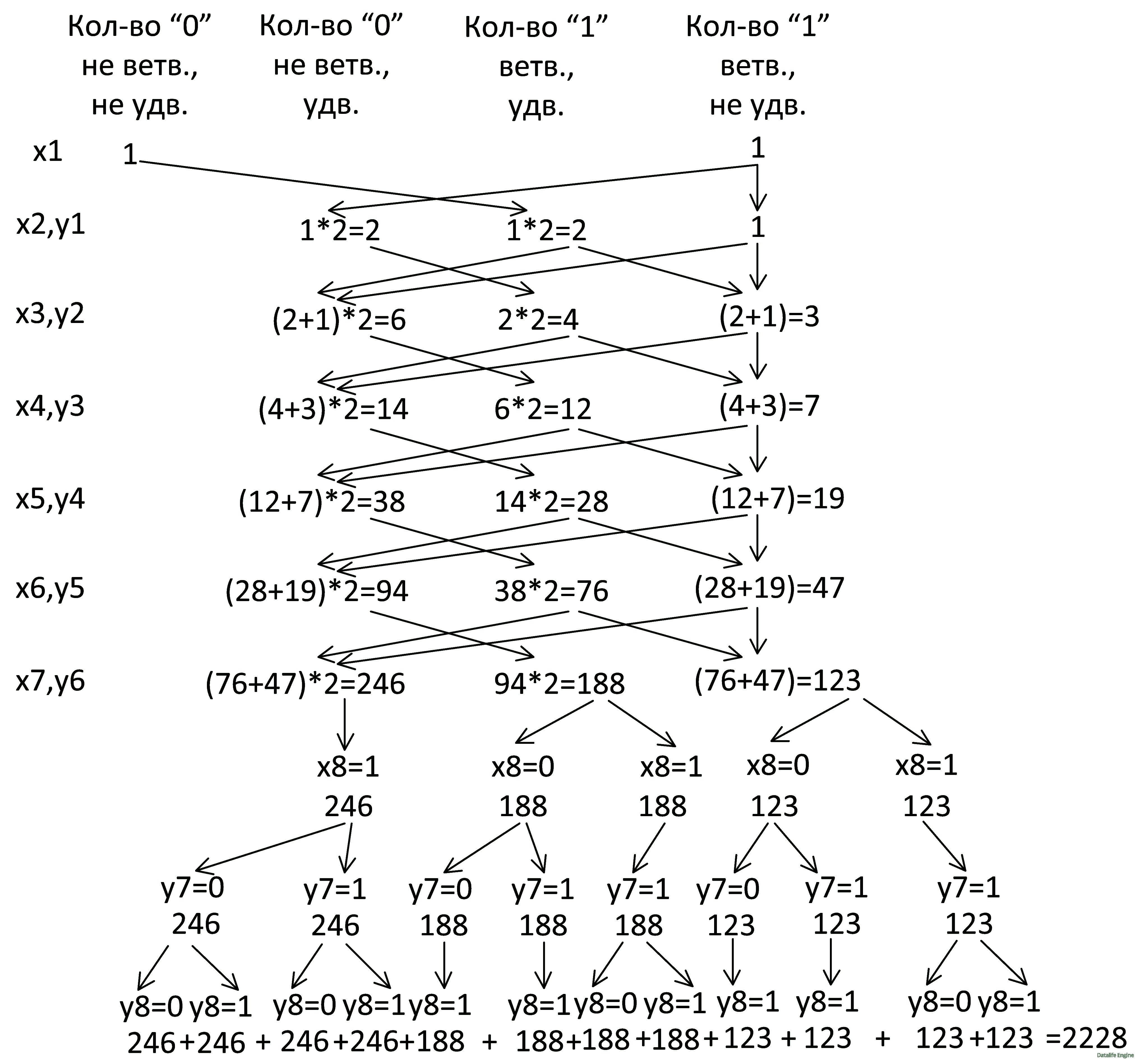
Ответ: 2228