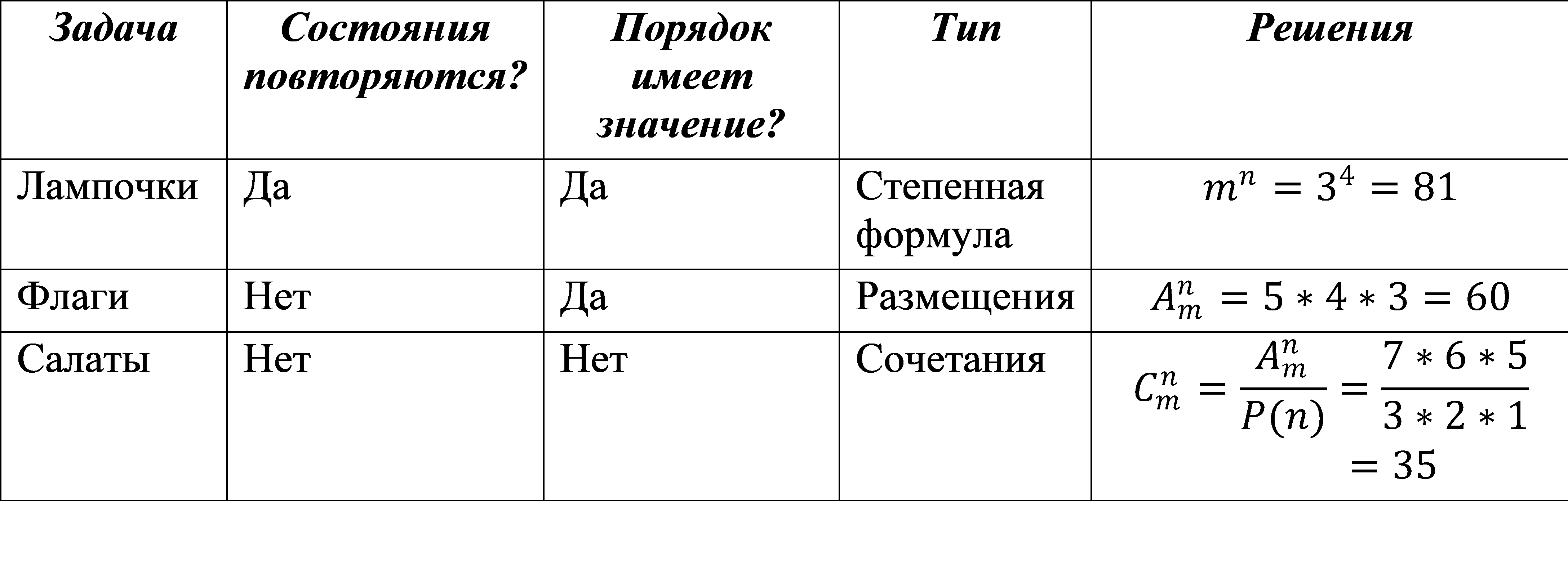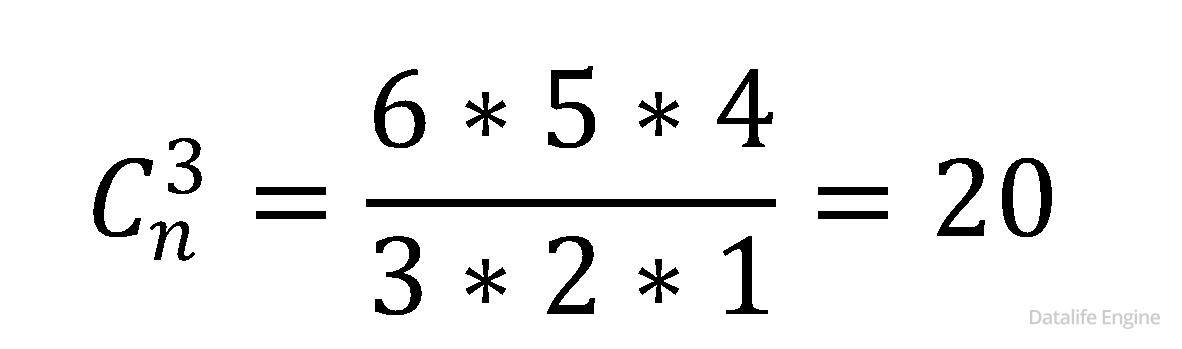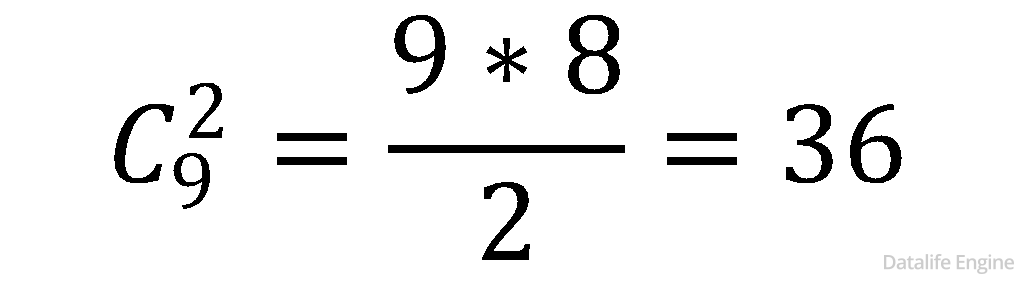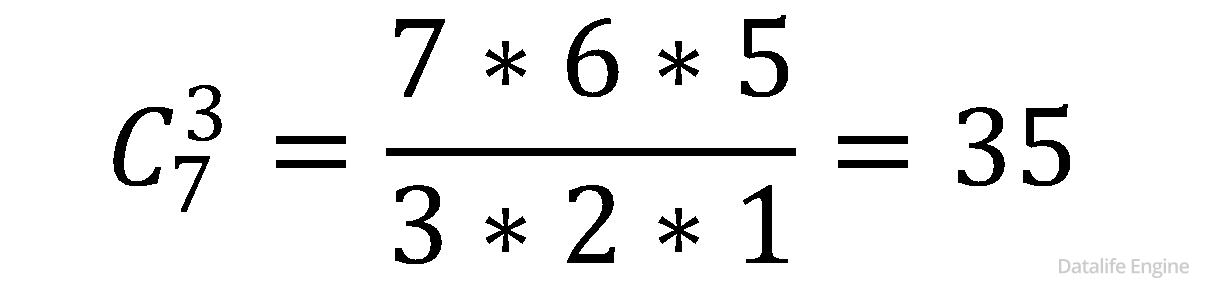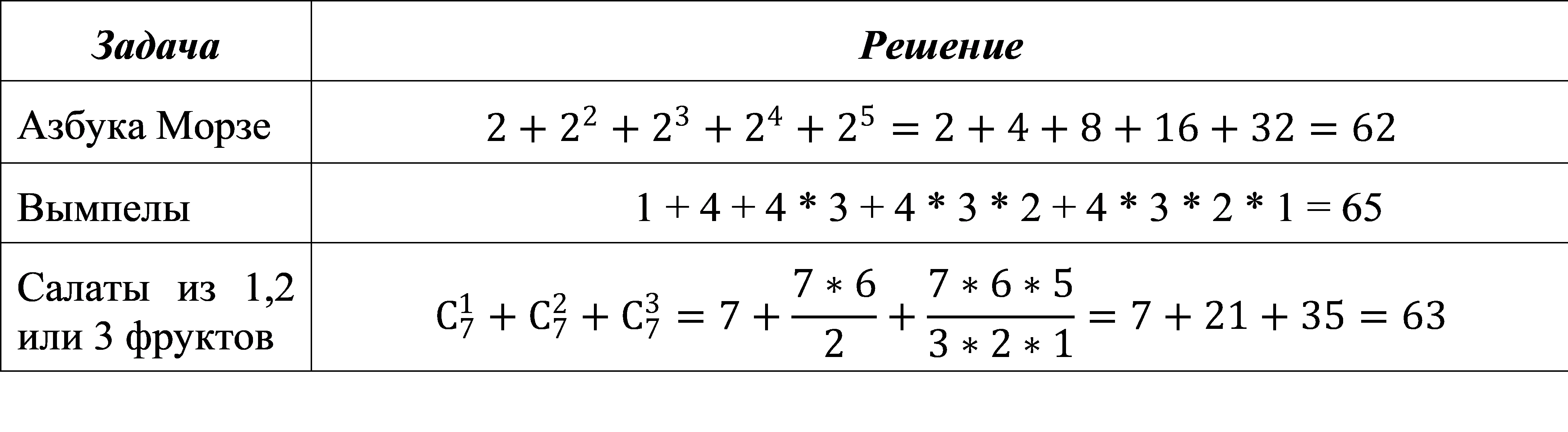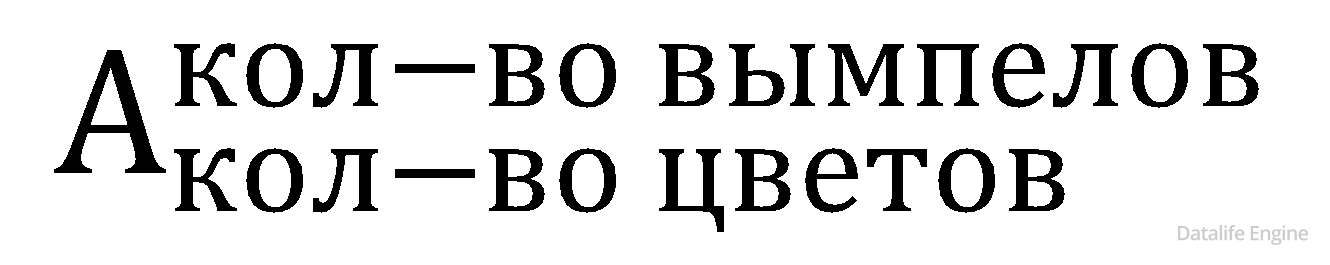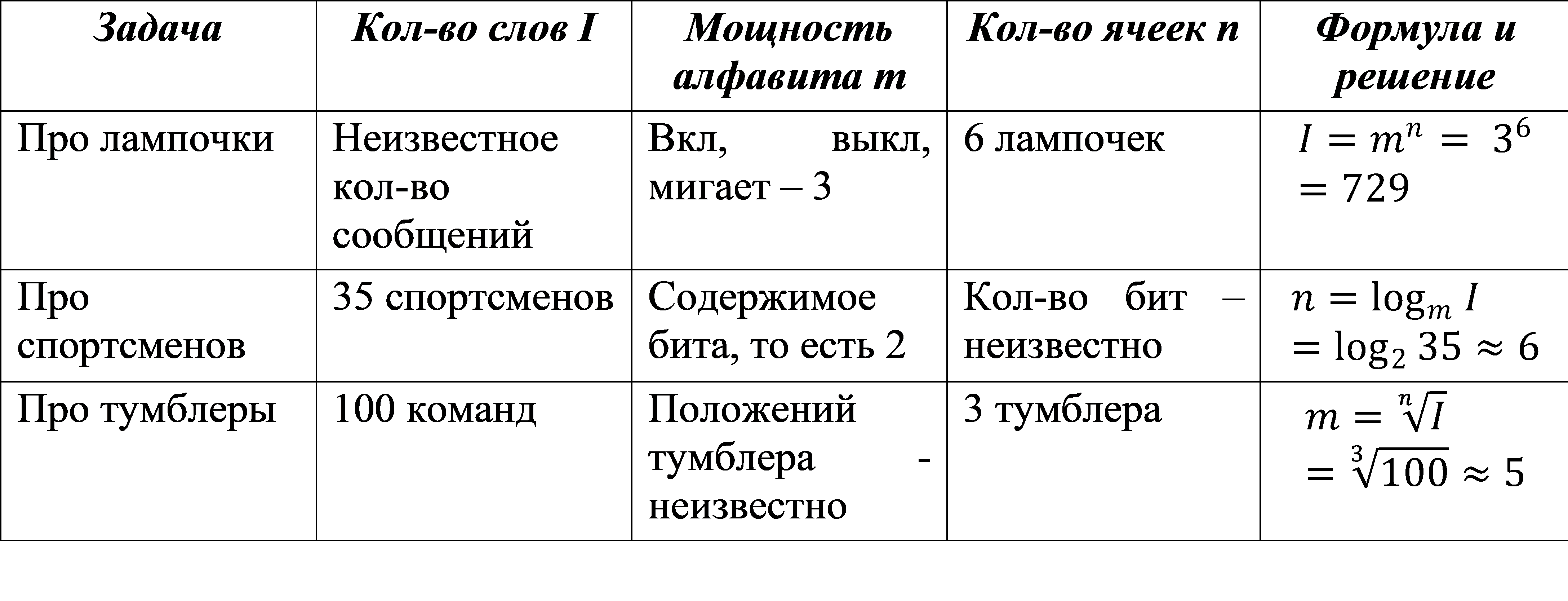Итак, начнем с повторения комбинаторных задач. Будем решать несколько задач одновременно (в книге они будут объединены в «задания»). По тексту будут встречаться следующие обозначения:
- Курсивом, например «Степенная формула», приведены основные идеи решения задачи. Их можно использовать как подсказки, но желательно не обращать на них внимание.
- «2.2.1» - номер этой или аналогичной задачи, уже решенной в данной книге. Если вы не можете их решить, то переходите в соответствующий параграф, в котором найдете решение. Если в книге задача не решена, то она имеет номер, начинающийся с «7.». Вскоре после таблицы вы найдете её решение.
Задание 7.1.1. Сравните и решите задачи (определите сходство и различие).
|
Лампочка может быть включенной, выключенной или мигающей. Сколько сообщений можно передать с помощью четырех таких лампочек? 2.2.1 |
Есть пять флагов разного цвета. Их мы можем вывешивать по одному на три мачты. Сколько сообщений мы можем передать? 2.2.2 |
В магазине продают фрукты 7 видов. Мы хотим купить три вида фруктов, чтобы сделать салат. Сколько разных салатов мы можем сделать? 2.2.3 |
Задание 7.1.2. Сравните и решите модификации следующей задачи (также сравните с задачами из задания 7.1.1.):
|
Алфавит состоит из четырех символов. Сколько можно составить шестибуквенных слов в следующих случаях: |
|||
|
1) Нет никаких ограничений на каждую букву. 2.2.1 |
2) буква А в слове ровно 1 раз |
3) буква А в слове ровно 2 раза |
4) буква А в слове ровно 3 раза |
|
(остальные – сколько угодно или не встречаются вовсе) 2.2.4 |
|||
Задача 7.1.3. Слово состоит из 10 символов. При этом буква А в нем встречается ровно 1 раз, B – ровно 2 раза, С – ровно 3 раза, D – ровно 4 раза. Сколько существует таких слов?
Задание 7.1.4. Сравните задачи из следующей таблицы (верхний ряд мы уже решали). Решите задачи из нижнего ряда.
|
Лампочка может быть включенной, выключенной или мигающей. Сколько сообщений можно передать с помощью пяти таких лампочек? 2.2.1 |
Есть пять флагов разного цвета. Их мы можем вывешивать на три мачты по одному. Сколько сообщений мы можем передать? 2.2.2 |
В магазине продают фрукты 7 видов. Мы хотим купить три вида фруктов, чтобы сделать салат. Сколько разных салатов мы можем сделать? 2.2.3 |
|
Азбука Морзе состоит из точек и тире. Сколько сообщений можно закодировать, если в сообщении не более 5 символов. 2.5.1 |
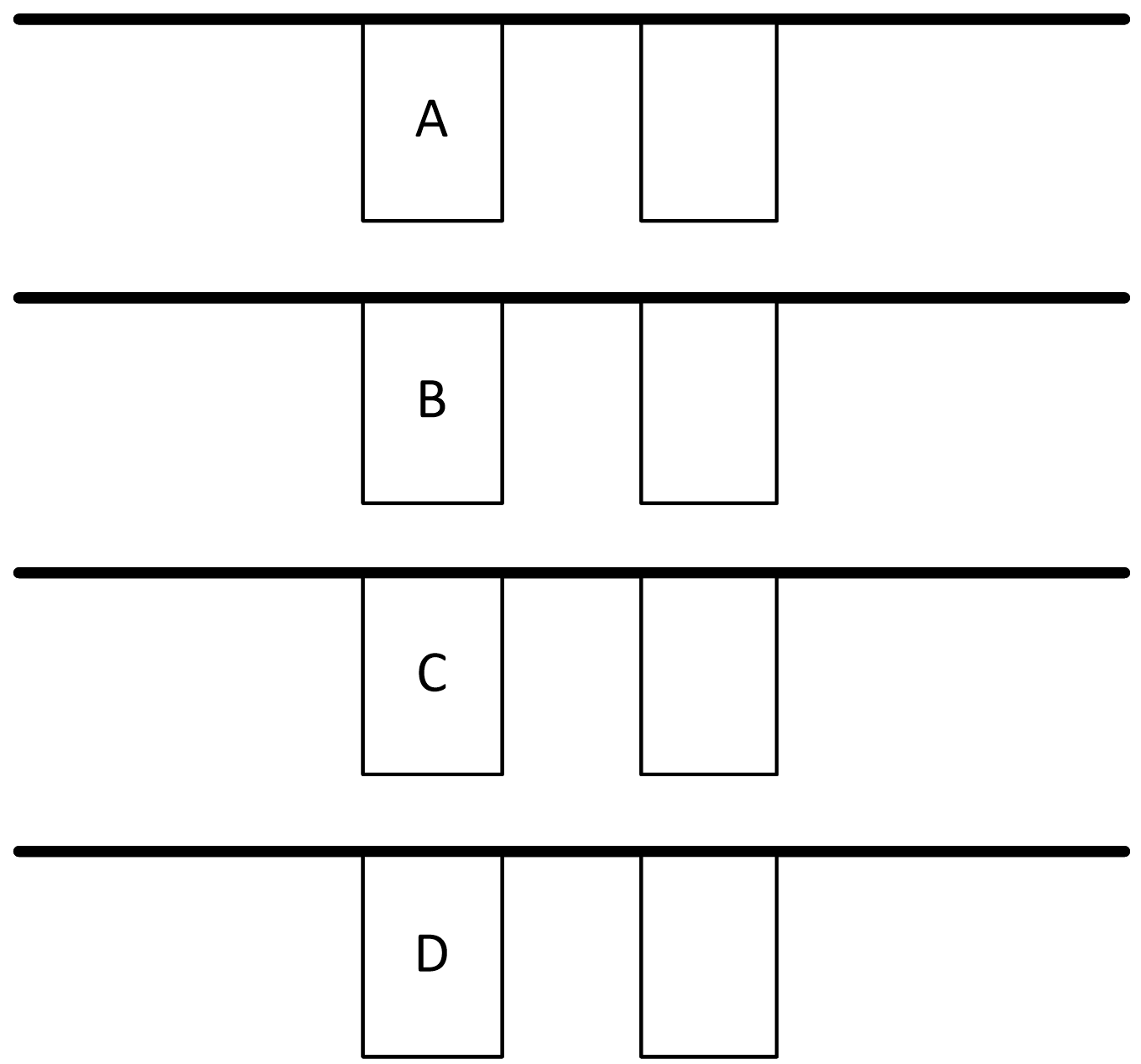
Есть четыре вымпела разного цвета. Мы можем их вывешивать на одну веревку. Сколько сообщений мы можем передать? (Пустая веревка – это тоже сообщение, на веревку может быть вывешено сразу несколько вымпелов, их порядок (слева или справа) имеет значение). 7.1.5. |
В магазине продают фрукты 7 видов. Мы хотим купить от одного до трёх видов фруктов, чтобы сделать салат. Сколько разных салатов мы можем сделать? 7.1.6. |
Задача 7.1.5. Есть четыре вымпела разного цвета. Мы можем их вывешивать на одну веревку. Сколько сообщений мы можем передать? (Пустая веревка – это тоже сообщение, на веревку может быть вывешено сразу несколько вымпелов, их порядок (слева или справа) имеет значение.)
Задание 7.1.7. Сравните и решите следующие задачи:
|
Лампочка может быть включенной, выключенной или мигающей. Сколько сообщений можно передать с помощью шести таких лампочек? 2.2.1 |
Сколько битов надо, чтобы закодировать номер победителя, если в соревновании участвовали 35 спортсменов? 2.2.5 |
Сколько положений может быть у тумблера, если в устройстве 100 команд, которые программируются с помощью трех тумблеров? 2.2.8 |
Задание 7.1.8. Сравните задачи из следующей таблицы. Найдите «ядро» задач – что является мощностью алфавита, словами и ячейками.
|
Метеостанция раз в день измеряет температуру. Сколько бит нужно на одно измерение, если диапазон измеряемой температуры от -64 до 64, а точность – 0,5 градуса. 2.2.9 |
Картинка размером 10 x 10 пикселей имеет палитру из 32 цветов. 1) Какой объем в битах занимает это изображение? 2.2.10 2) Сколько картинок в принципе можно составить (напишите выражение, не вычисляя)? 2.2.10-примечание |
Идет двухканальная запись звука с частотой дискретизации 100 Гц, количеством уровней дискретизации, равным 64, и продолжительностью 5 минут. Какой объем сигнала в байтах? 2.2.11 |
|
В соревновании участвуют 20 спортсменов. 1) Сколько бит надо, чтобы закодировать номера трех чемпионов? 2.2.5 2) Сколько может быть вариантов списков чемпионов? 2.2.5-примечание |
Автомобильный номер длиной 7 символов составляют из заглавных букв (используются только 33 различных буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов. 1) Определите объём памяти, отводимый этой программой для записи 125 номеров. 2.2.13 2) Сколько всего может быть автомобильных номеров? 2.2.13-примечание. |
|