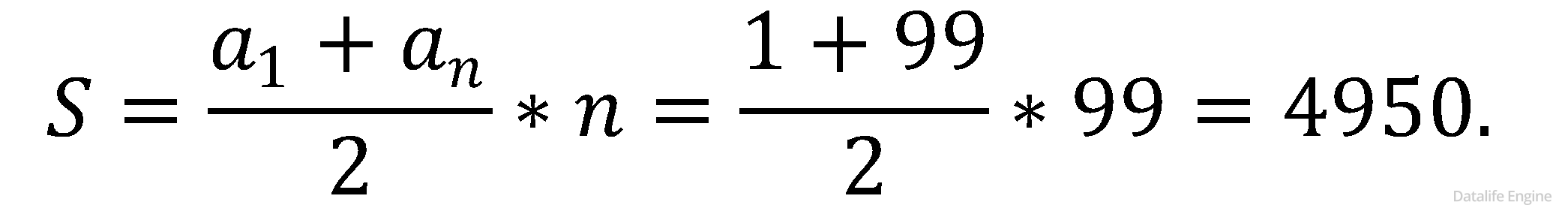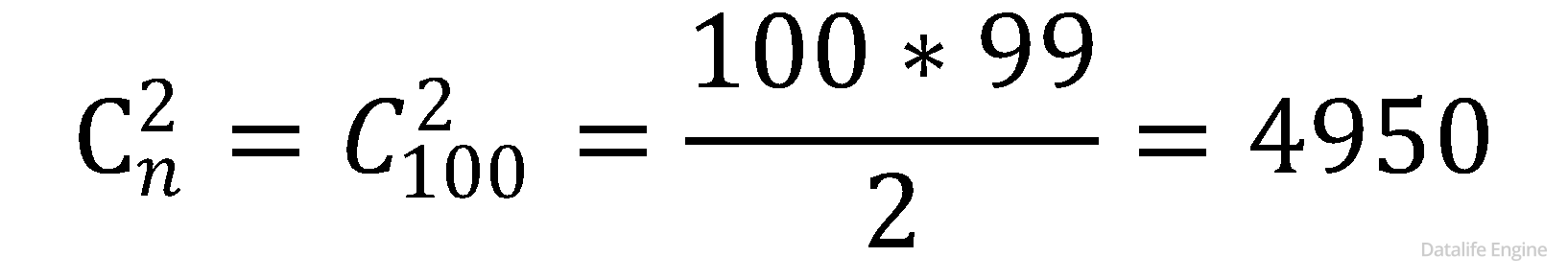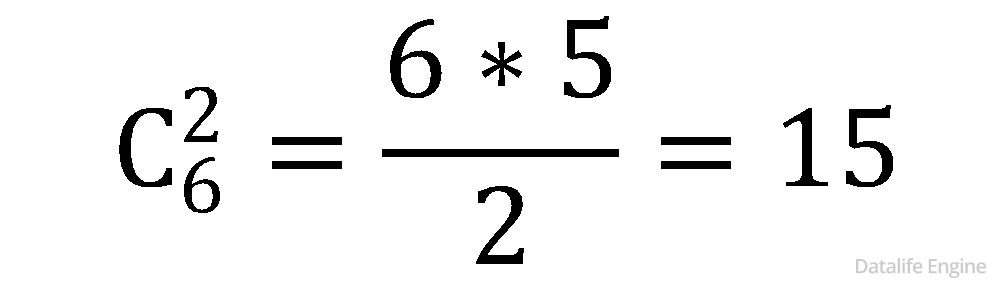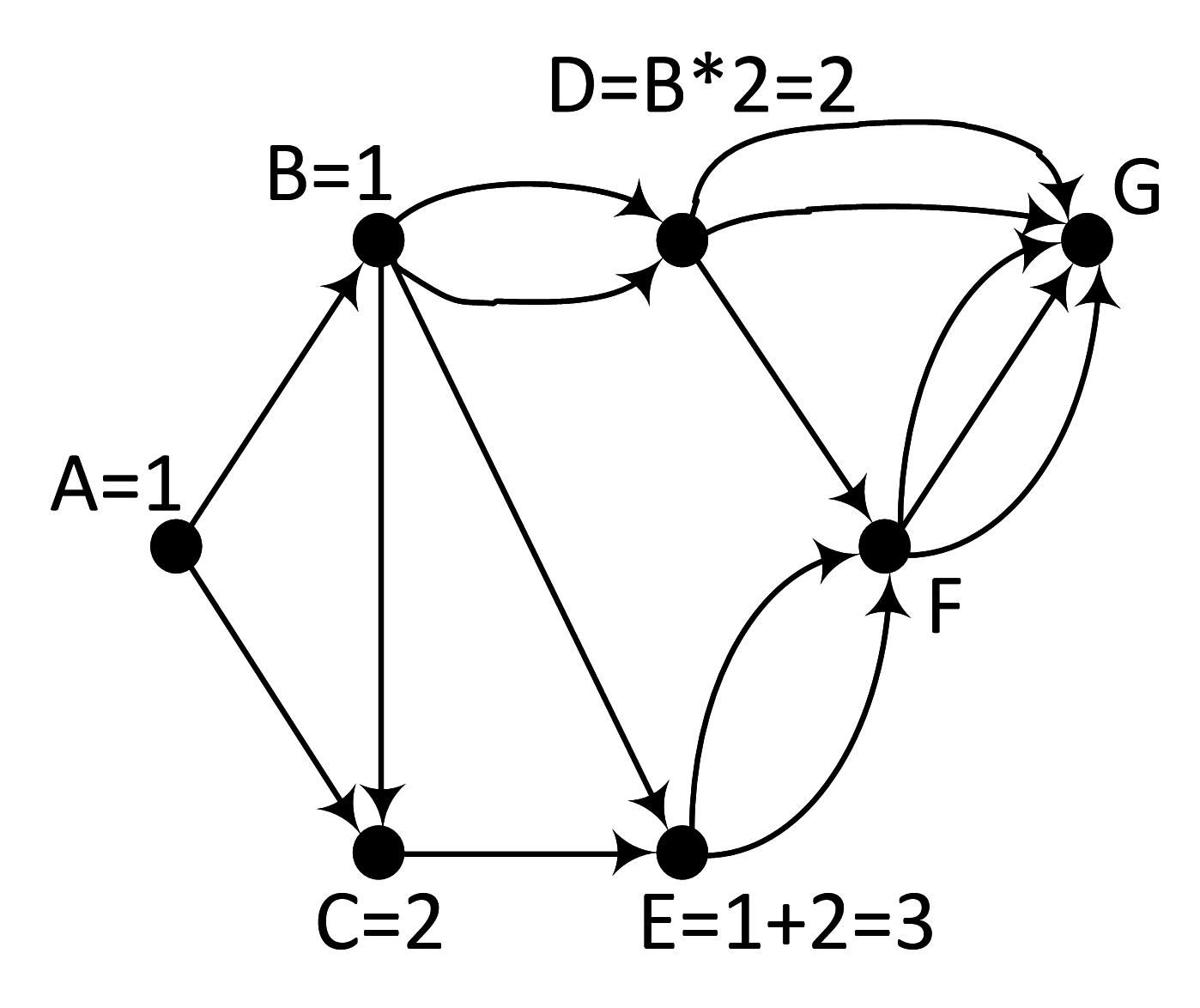В этом параграфе рассматриваются либо задачи, которых нет в ЕГЭ, либо усложненные задачи из ЕГЭ, поэтому вы можете его пропустить. Польза от параграфа заключается в том, что некоторые ученики вообще не видят «комбинаторную суть» задач, а значит, не догадываются о том, что для решения задачи можно применить формулы комбинаторики. После изучения этих задач вы научитесь видеть комбинаторику буквально во всем!
Последняя задача параграфа – это лёгкое усложнение задачи ЕГЭ на поиск количества путей в графе. Я рекомендую её решить (можете попробовать её решить с самого начала). Она формирует правильный механизм мышления для задач на логические уравнения, в которых используются деревья решений.
Задача 7.2.1. Граф состоит из 11 вершин. Первая связана со второй одним путем, вторая с третьим – двумя, третья с четвертым – тремя и т.д. Сколько путей ведет из первой вершины в последнюю?

Найдите аналогию с первыми тремя задачами комбинаторики 2.2.1, 2.2.2, 2.2.3.
Обозначим левый фрагмент графа буквами:
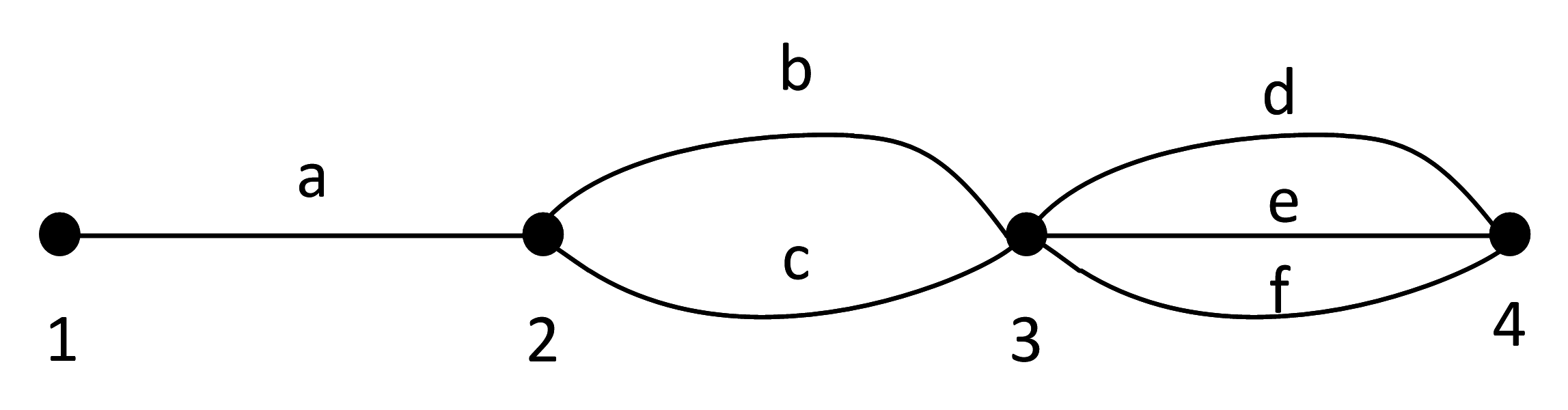
Из вершины 1 в вершину 2 ведет только один путь:
a
Из вершины 1 в вершину 3 ведут два пути:
ab
ac
Из вершины 1 в вершину 4 ведут шесть путей:
abd
abe
abf
acd
ace
acf
Видно, что количество путей утроилось. Это произошло потому, что мы взяли два пути из 1 в 3 и к каждому из них добавили по три ребра, которые идут из 3 в 4.
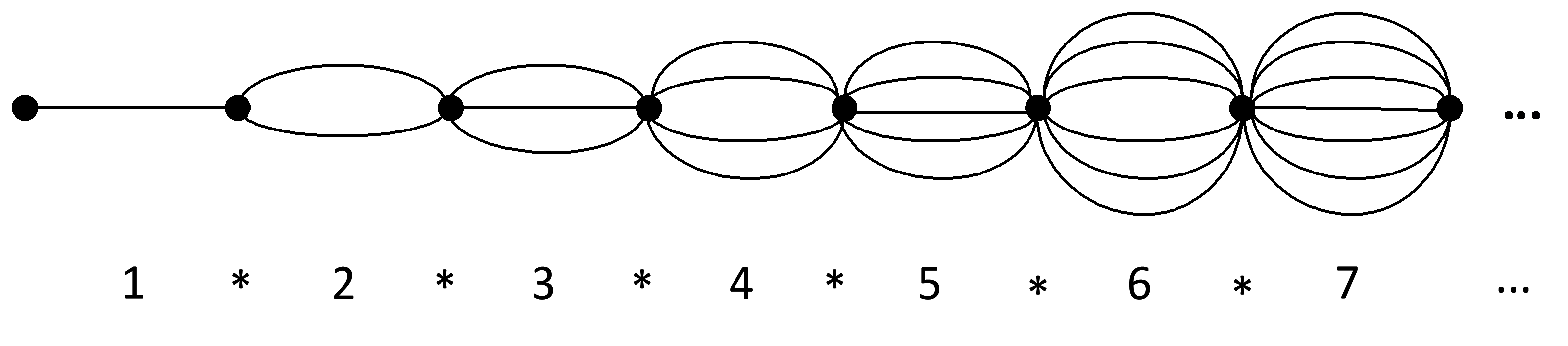
Из 10 вершины в 11 идут 10 путей, таким образом, количество путей равно 10! = 362880.
Ответ: 362880
Примечание. Полезно найти аналогию с задачами комбинаторики.
Заменим ребра из одной вершины к другой на ячейки:
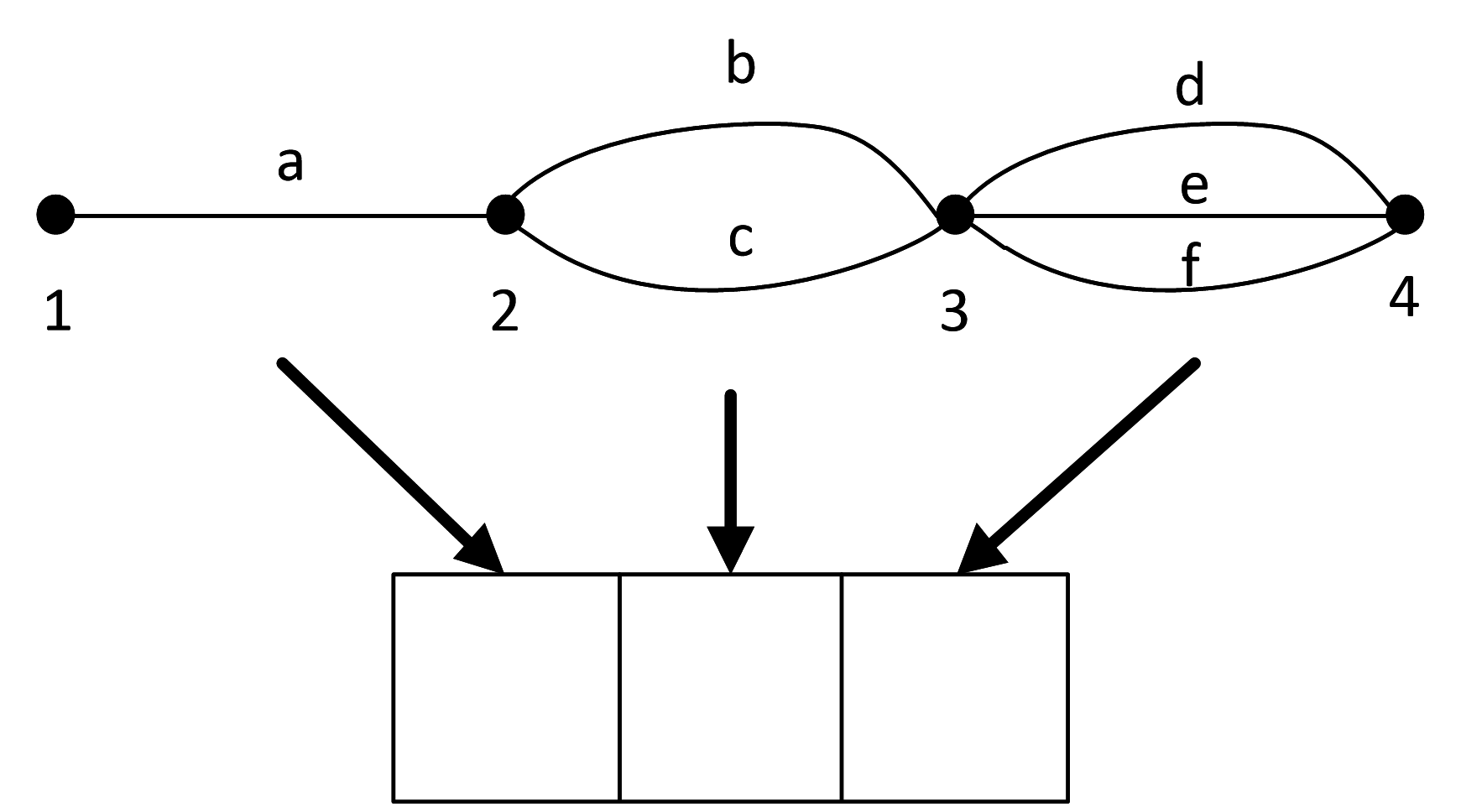
Тогда названия ребер будут алфавитом в соответствующих ячейках:
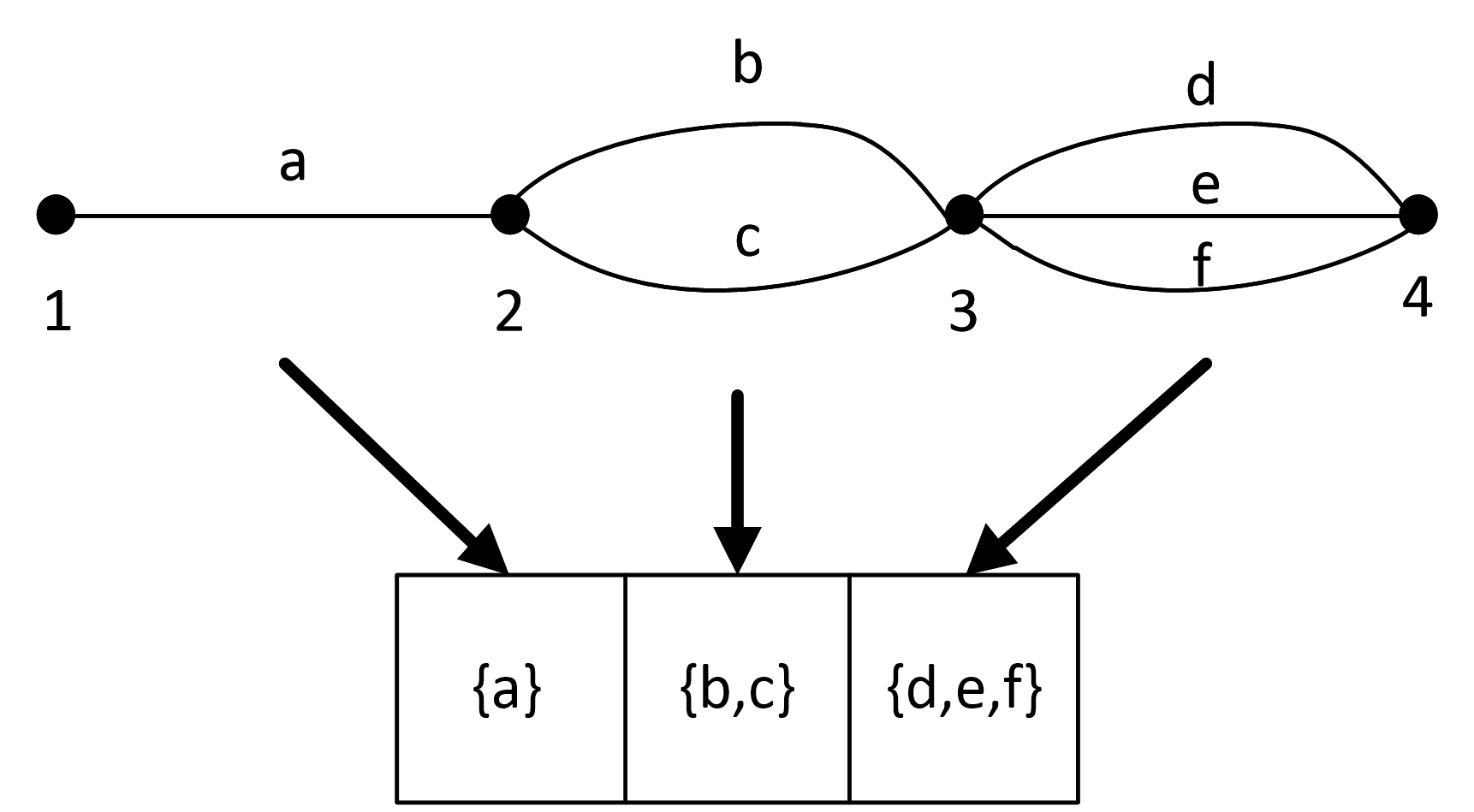
То есть мы имеем дело с последовательностью ячеек с увеличивающимися мощностями алфавита:
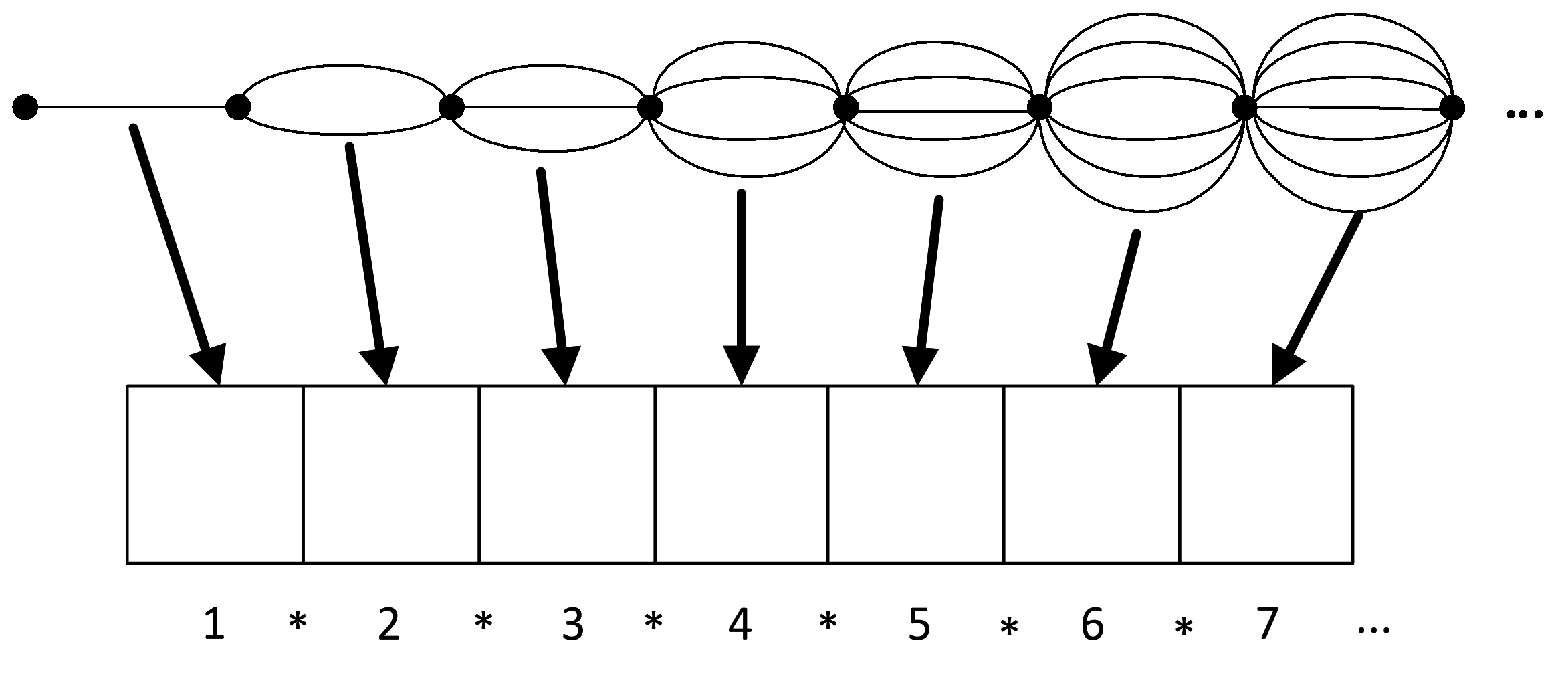
Комбинаторные задачи «любят маскироваться» под другие виды. Умение увидеть «комбинаторную суть» задачи – важный навык. Например, в задачах на логические уравнения (4.5.4), там, где мы переходили к новым обозначениям, строили дерево, а затем возвращались к исходным обозначениям, мы действовали точно так же.
Задача 7.2.2.
|
Полным графом называют граф, у которого любая пара вершин соединена ребром. Пусть граф состоит из 100 вершин. Сколько ребер в графе?
|
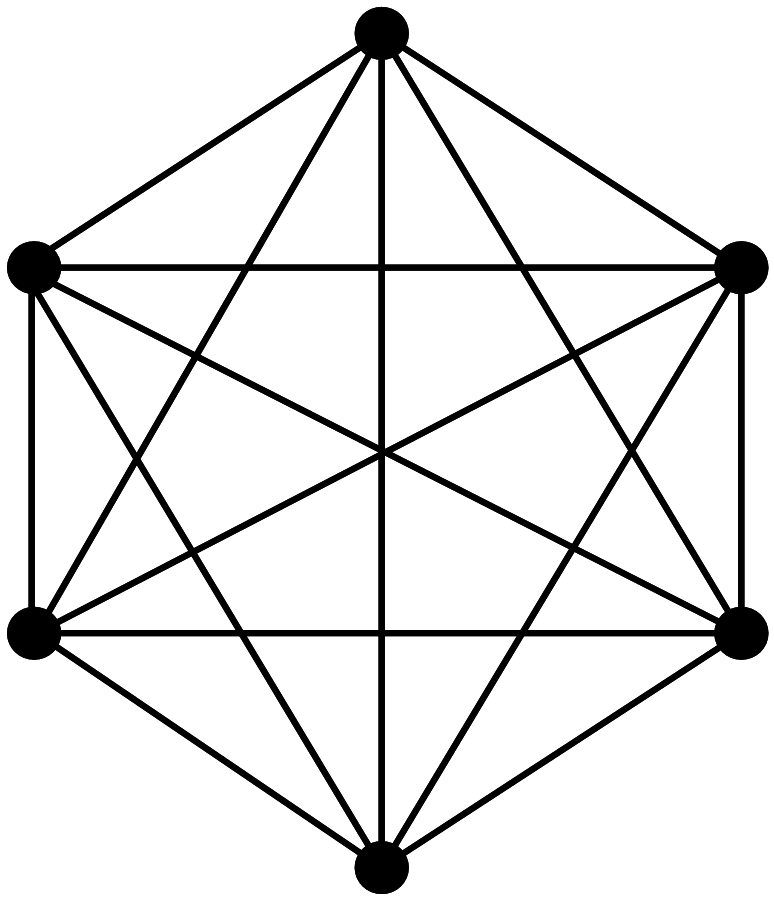
|
Это задача на сочетание (combination) или на арифметическую прогрессию.
|
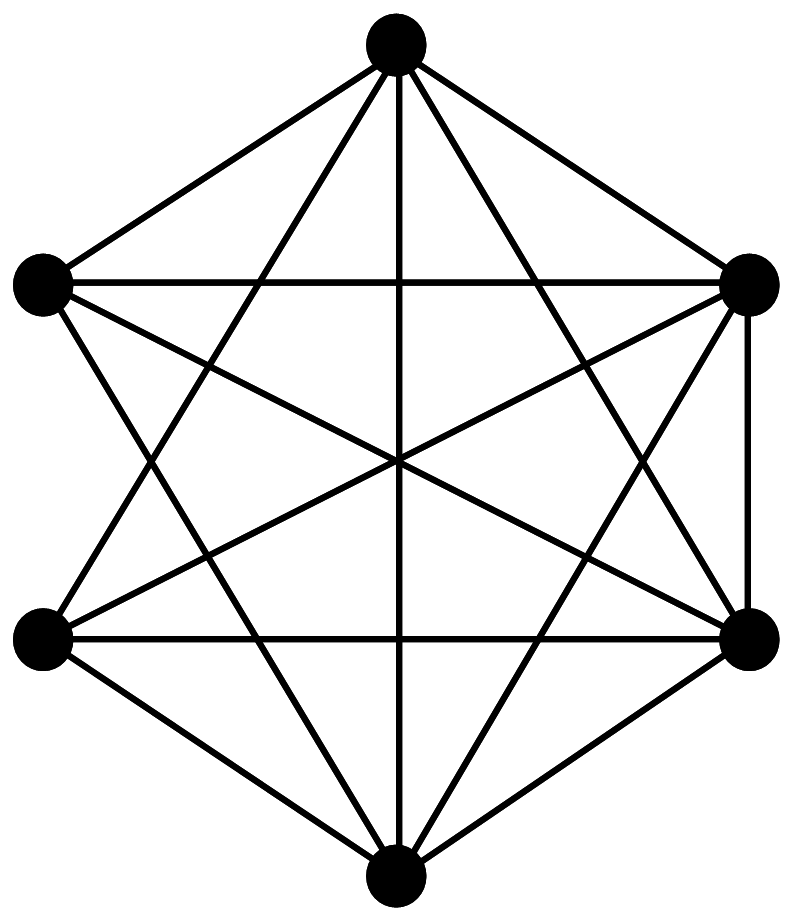
Рассмотрим урезанный вариант графа, состоящий из 6 вершин. Уберем все ребра и начнем рисовать их заново:
|

|
|
Возьмем одну из вершин и проведем от неё все ребра (получится 5 ребер):
|
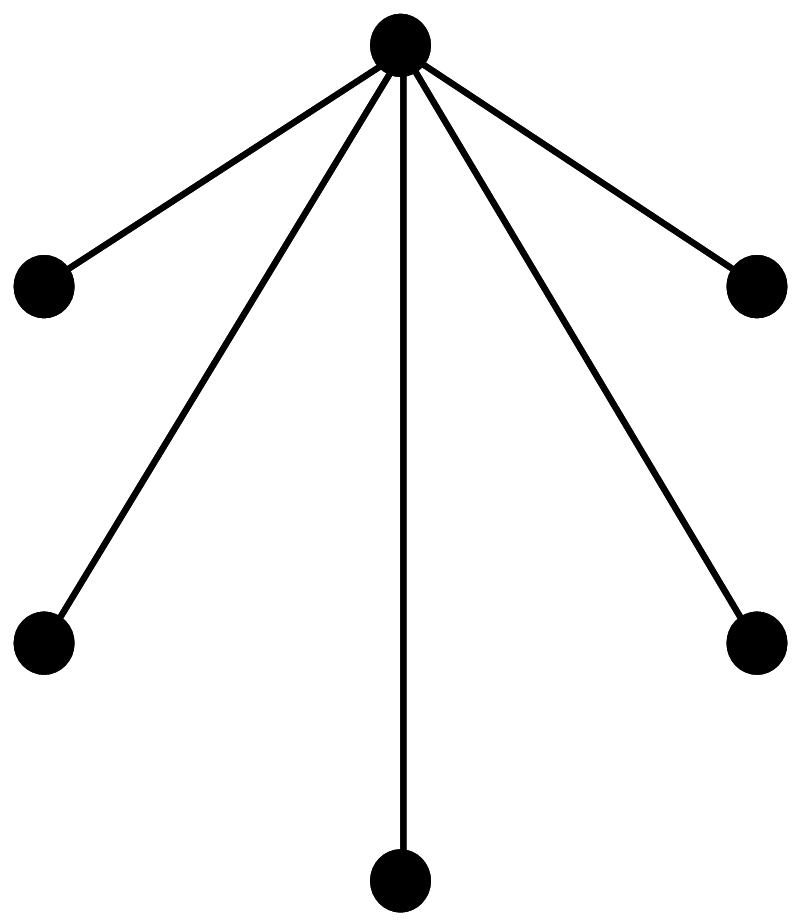
|
|
Возьмем вторую вершину и проведем от неё все ребра (получится 4 ребра, так как к первой вершине ребро уже было проведено). Добавим эти 4 ребра к 5 ребрам, найденным на предыдущем этапе:
5+4
|

|
|
От третьей вершины получится провести три ребра:
5 + 4 + 3
|
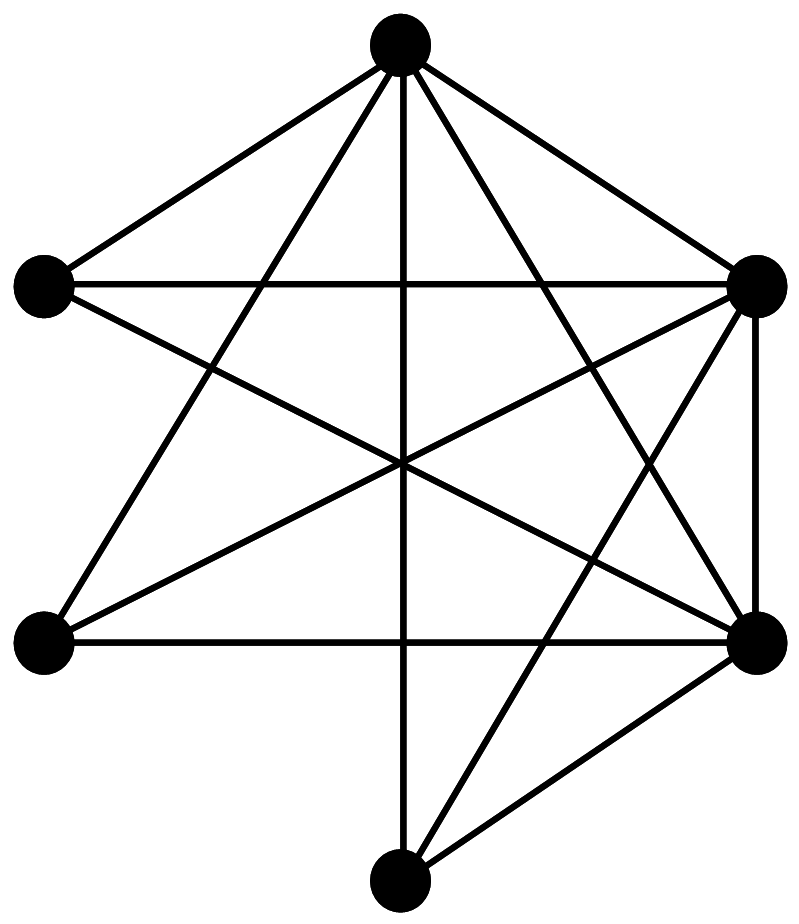
|
|
От четвертой вершины - два ребра:
5 + 4 + 3 + 2
|
|
|
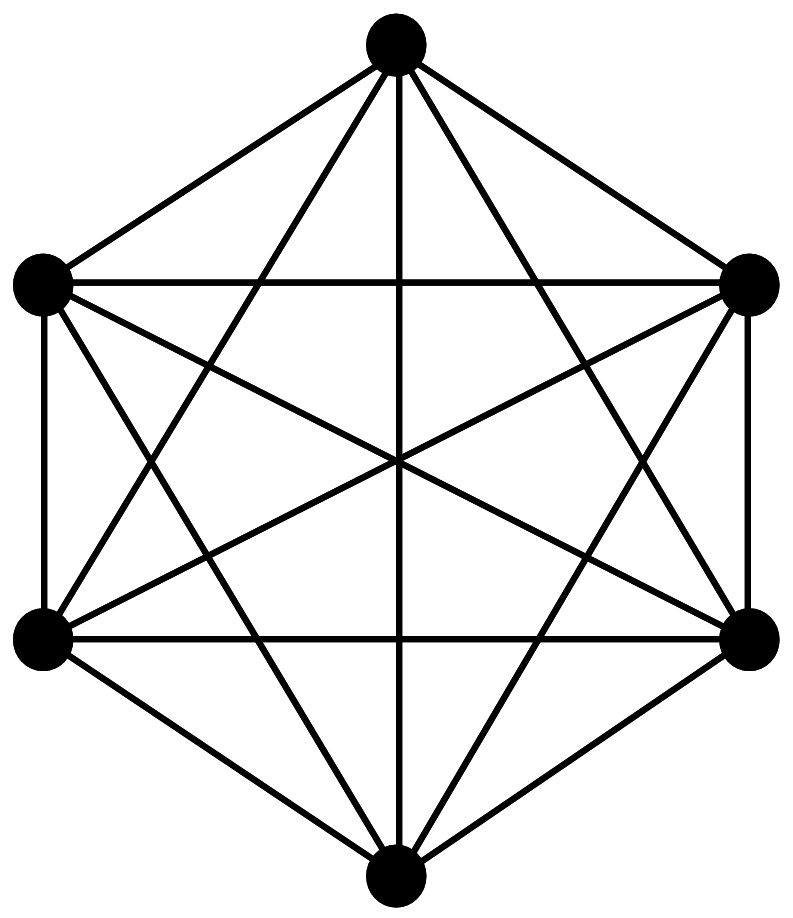
От последней вершины - одно ребро:
5 + 4 + 3 + 2 + 1 = 15
|
|
Для шести вершин мы получили сумму от 5 до 1.
Аналогично, для 100 вершин мы получим сумму чисел от 99 до 1.
1 + 2 + 3 + … + 97 + 98 + 99 – это сумма членов арифметической прогрессии.
Если вы забыли формулу суммы членов арифметической прогрессии, то воспользуемся свойством «от перестановки мест слагаемых сумма не меняется» и сложим первое слагаемое с последним, второе – с предпоследним, и т.д:
1 + 99 = 100
2 + 98 = 100
3 + 97 = 100.
Всего таких пар 49 и еще одиночное центральное число 50.
Получаем: 100 * 49 + 50 = 4950.
Или по формуле суммы членов арифметической прогрессии:
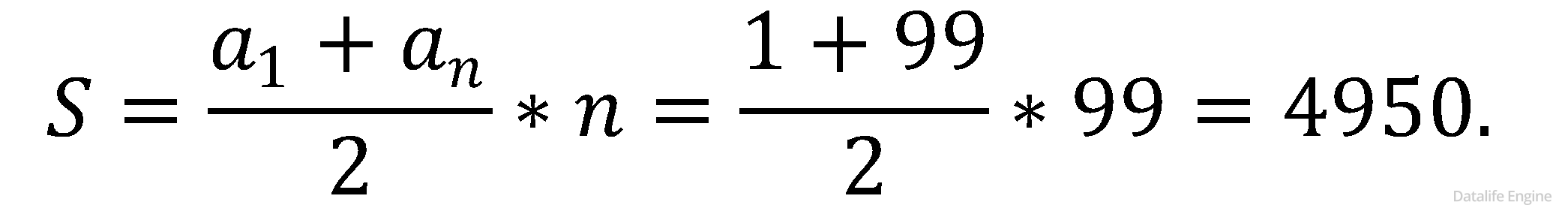
Ответ: 4950
Подумаем, что представляет собой задача с точки зрения комбинаторики. Ребро соединяет пару вершин. Поскольку ребро не направлено, то если нам даны вершины A и B, то ребра АB и BA – это одно и то же ребро. Поскольку граф полный, то любые две вершины соединены между собой.
Задача представляет собой подсчет количества выборок из n предметов (вершин) по два. Причем порядок не имеет значения. То есть это – задача на сочетания:
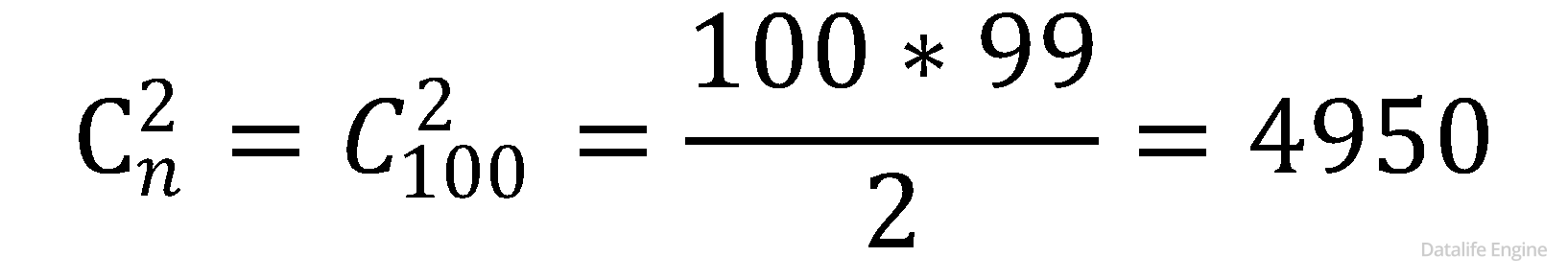
Примечания:
- Комбинаторный способ менее очевиден, но более полезен с точки зрения «видения комбинаторики». В частности, он пригодится в следующей задаче. А вот метод с арифметической прогрессией там будет уже бесполезным.
- Полезно еще раз взглянуть на предыдущую задачу. Там обсчет шел с помощью факториала. Решение этих двух задач подряд поможет сформировать навык различения ситуаций, когда нужно сложение, а когда – умножение.
- Эта задача полезна для решения одной разновидности задач на логические уравнения (той, где строится несколько деревьев, ветки которых потом соединяются) – 4.5.11.
Задача 7.2.3. Симплексом является простейший объект в многомерном пространстве:
|
0 измерений – точка:

|
1 измерение – отрезок:

|
2 измерения – треугольник:

|
3 измерения – тетраэдр

|
|
1 вершина
|
2 вершины,
1 ребро
|
3 вершины,
3 ребра
1 грань
|
4 вершины
6 ребер
4 грани
1 тело (гипергрань)
|
Сколько разных элементов (вершин, ребер, граней, гиперграней…) имеет симплекс в шестимерном пространстве?
Это задача на сочетания, быстрее всего она решается с помощью треугольника Паскаля.
Заметим, что в симплексах с увеличением размерности пространства на одно измерение происходит увеличение количества вершин на одну. Трехмерный симплекс (тетраэдр) имеет 4 вершины, четырехмерный – 5 вершин, пятимерный – 6 вершин.
Заметим, что в симплексах ребра соединяют все вершины (то есть любая пара вершин обязательно соединена ребром). Можно рассматривать симплекс как полный граф. Но это же предыдущая решенная нами задача!
Способ 1. Можно решить её как сумму членов арифметической прогрессии.
Берем симплекс размерности 0 (точку).

Добавляем еще одну вершину (симплекс размерности 1). Связываем ребром с предыдущей вершиной:

Кол-во ребер = 1.
Чтобы получить симплекс размерности 2 (треугольник), добавляем вершину и связываем её двумя ребрами с имеющимися вершинами:

Кол-во ребер = 1 + 2 = 3.
В трехмерном пространстве берем треугольник, добавляем еще одну вершину и связываем её со всеми тремя вершинами треугольника тремя ребрами, чтобы получить тетраэдр:

Кол-во ребер = 1 + 2 + 3 = 6.
Аналогично в четырехмерном симплексе берем тетраэдр, добавляем пятую точку и четырьмя ребрами связываем её с вершинами тетраэдра:
Кол-во ребер = 1 + 2 + 3 + 4 = 10.
В пятимерном пространстве:
Кол-во ребер = 1 + 2 + 3 + 4 + 5 = 15.
Способ 2. Комбинаторный.
Ребра можно рассматривать как сочетания из двух вершин, где порядок не имеет значения:
Кол-во ребер 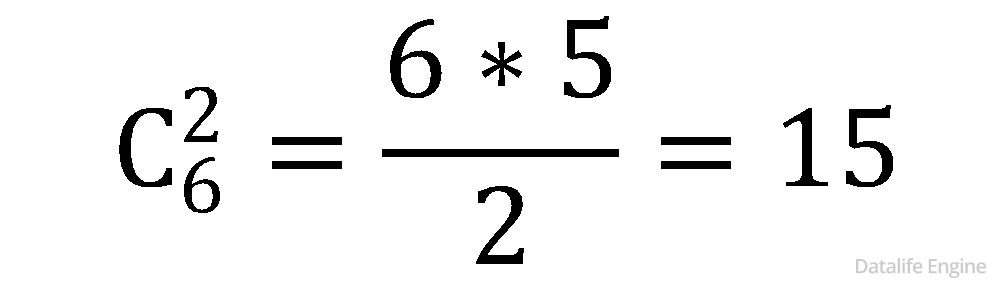
Этот метод (по сравнению с арифметической прогрессией) более перспективен для подсчета количества других элементов симплекса.
Продолжение хода решения.
Если ребра можно рассматривать как сочетания из двух вершин, то грани – как сочетания трех вершин:
Количество граней 
Количество гиперграней (тетраэдров)

И т.д.
Не будем торопиться выполнять вычисления по формулам сочетаний, вспомним, что быстрее для вычислений использовать треугольник Паскаля:
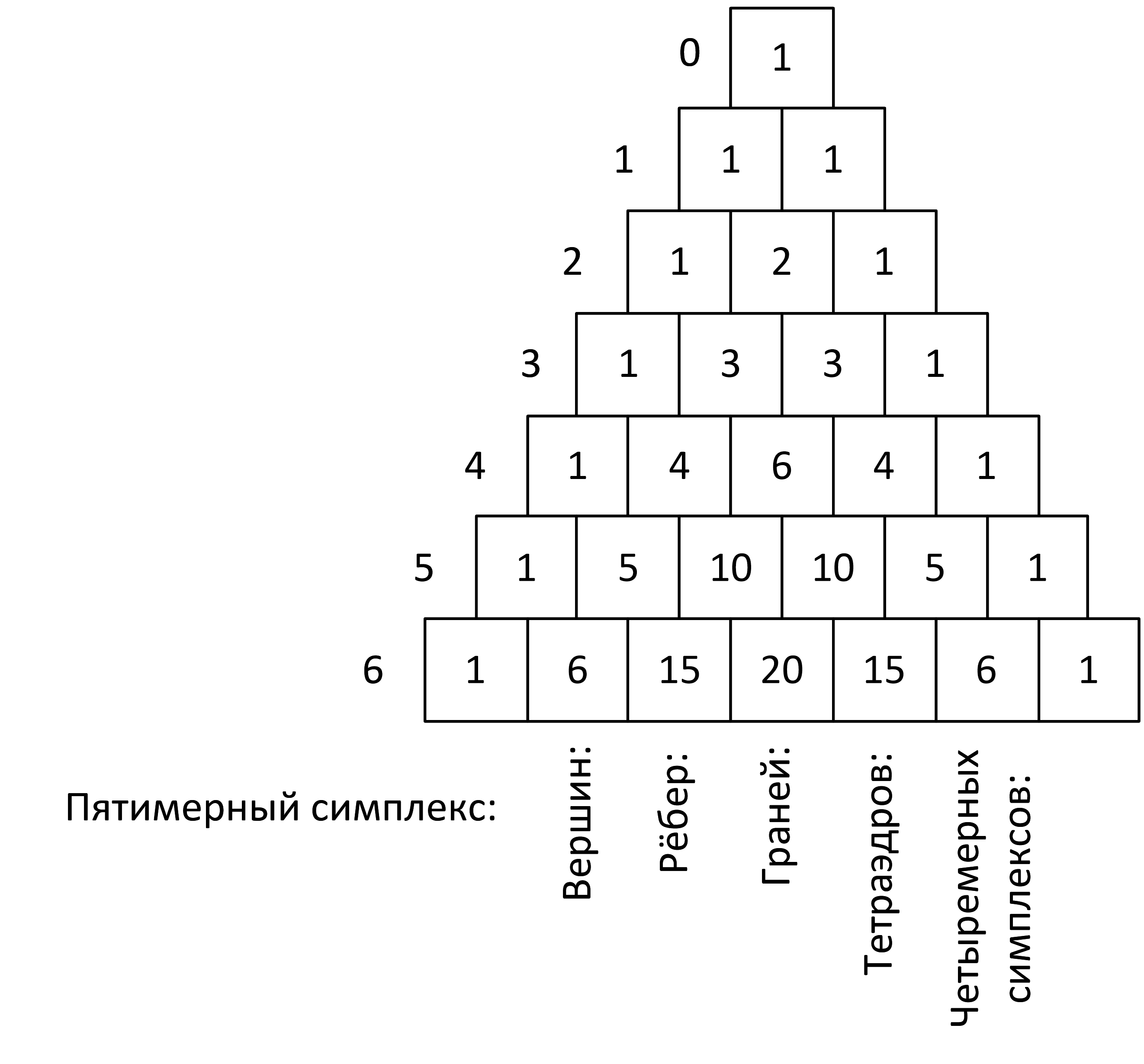
Заметим, что для обсчета пятимерного симплекса нам пришлось нарисовать семистрочный треугольник Паскаля, так как нумерация строк в треугольнике Паскаля начинается с нуля, а вершин (то есть комбинируемых объектов) в симплексе на 1 больше, чем размерность его пространства.
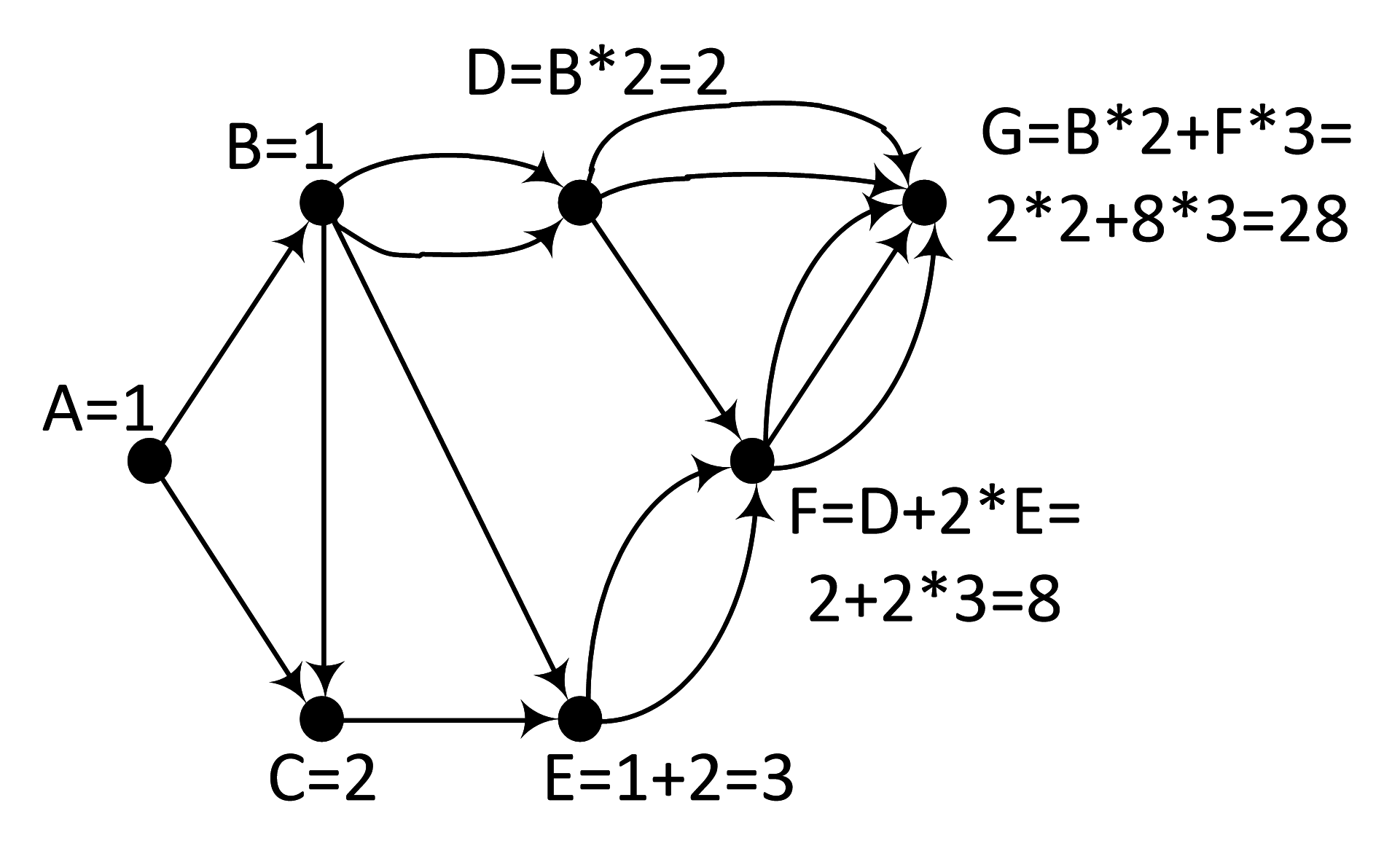
Задача 7.2.4. Сколько существует путей из А в G?

Эта задача – развитие задач 3.1.1 и 7.2.1.
Начнем обсчет графа, ставя у вершин метки количества путей из А:
- Ставим в А метку 1 (это означает, что из А в А можно попасть одним способом – оставшись там, где мы были):
|

|
- В B из А можно попасть одним путём (переписываем в B метку из А):
|

|
- В С из А можно попасть двумя путями (прямым из А и опосредованно через B). Можно предположить, что
С=A+B
|

|
- Если верна гипотеза о том, что метка при вершине равна сумме меток входящих вершин, то
Е = B + C = 3.
Убедимся, что это так, перечислив все пути из А в E:
ABE
ABCE
ACE
|

|
- Если из одной вершины в другую ведут два ребра, то количество путей удваивается:
D = B * 2 = 2
|
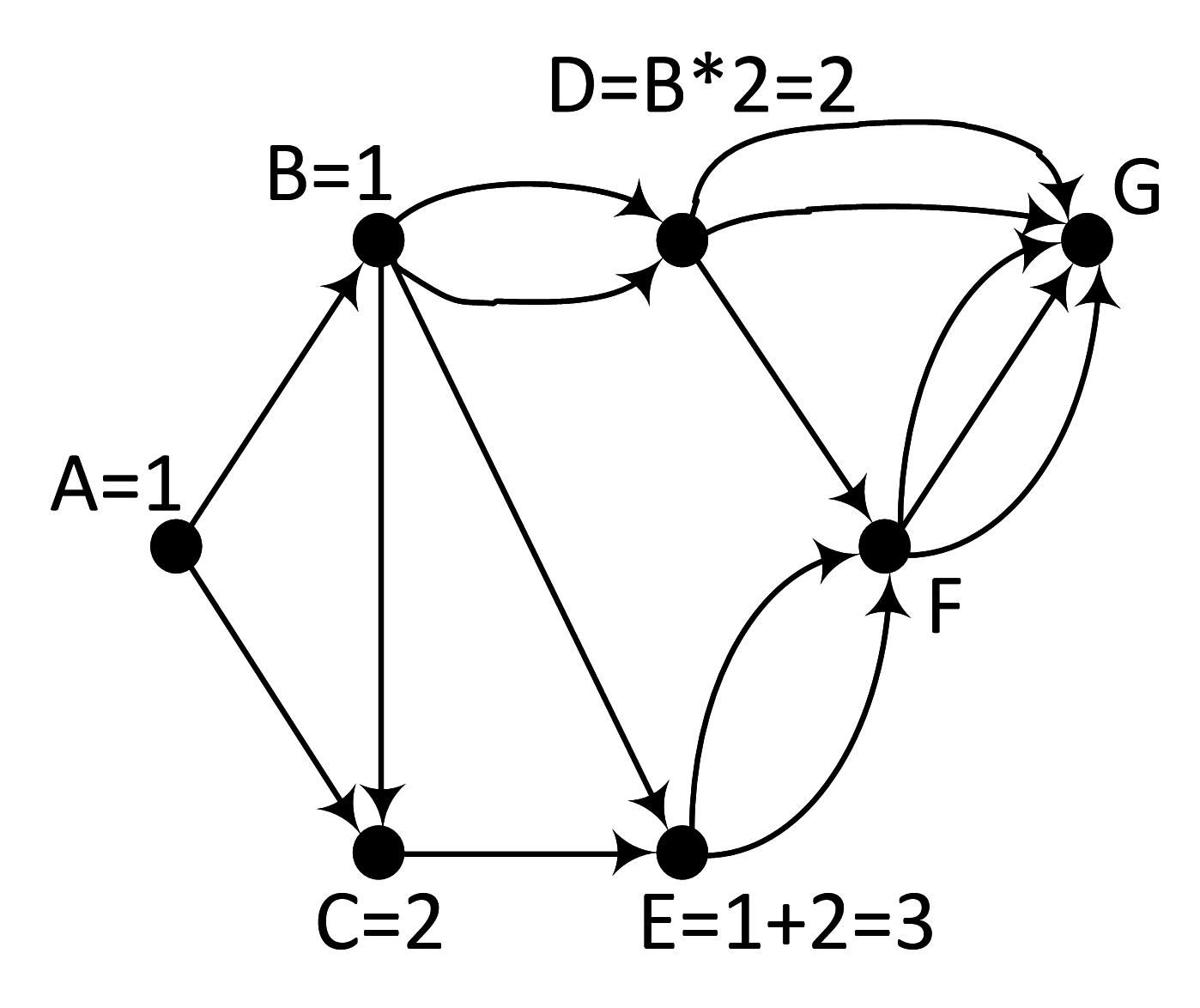
|
- Обсчитываем F:
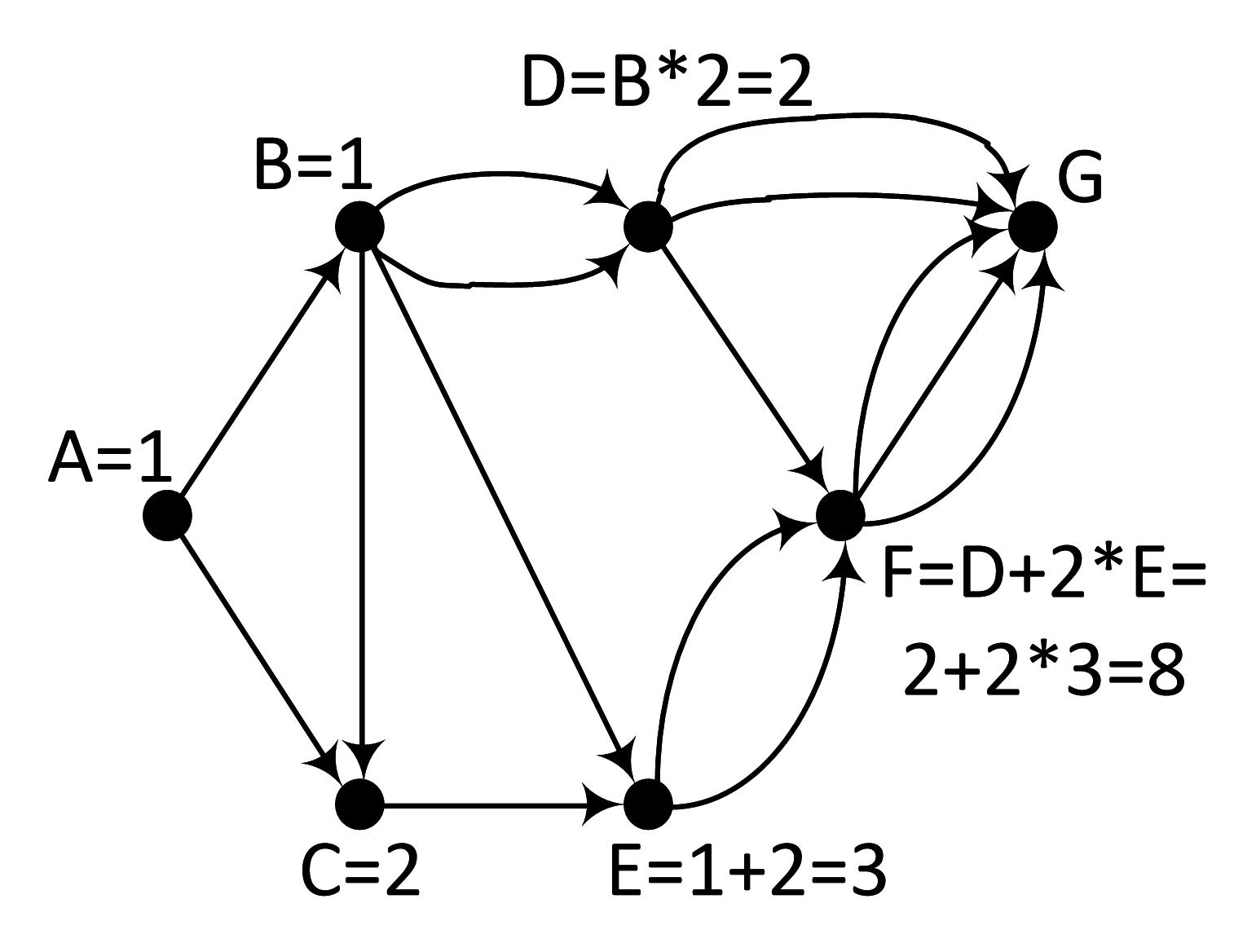
|
- Обсчитываем G:
|
Ответ: 28