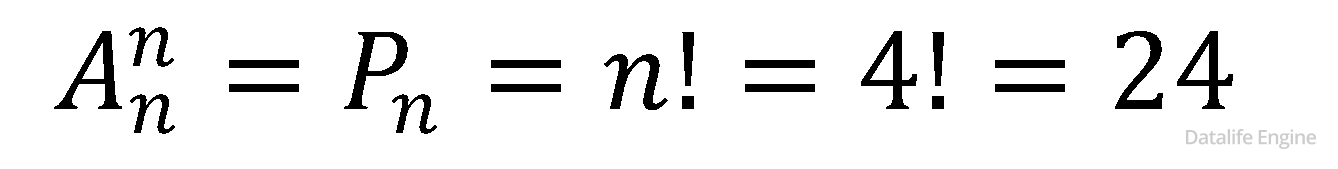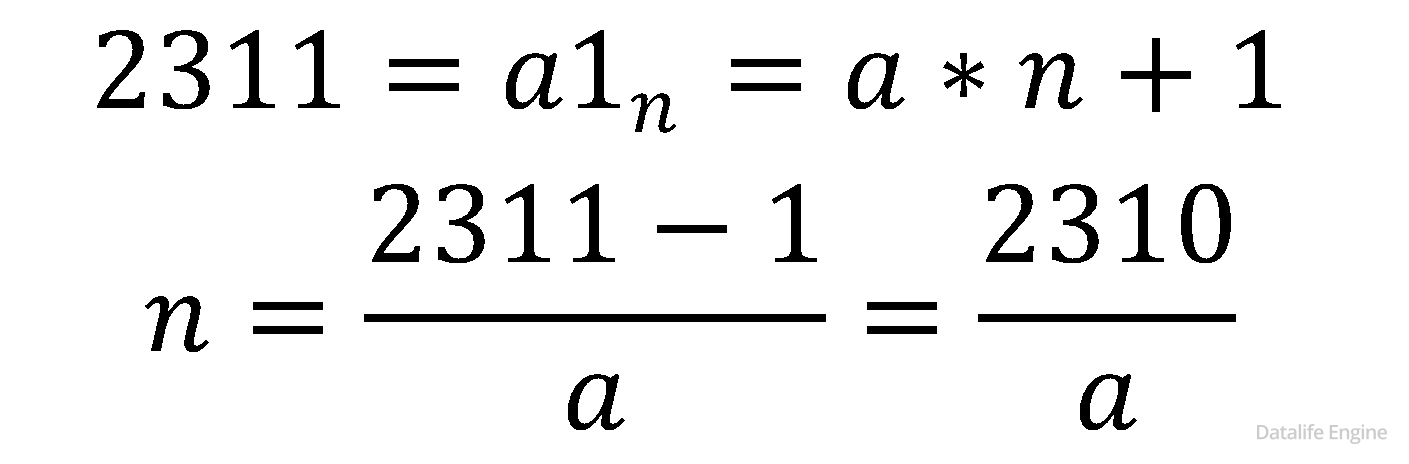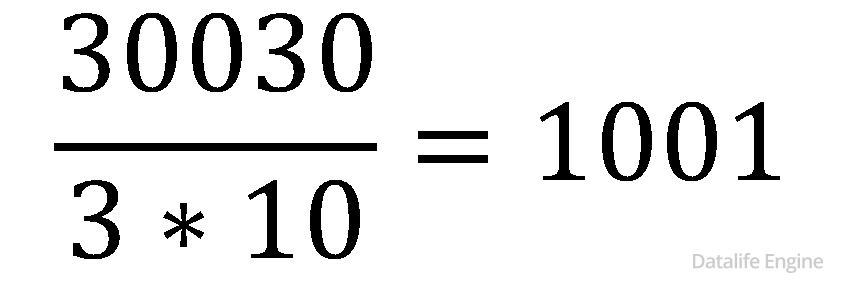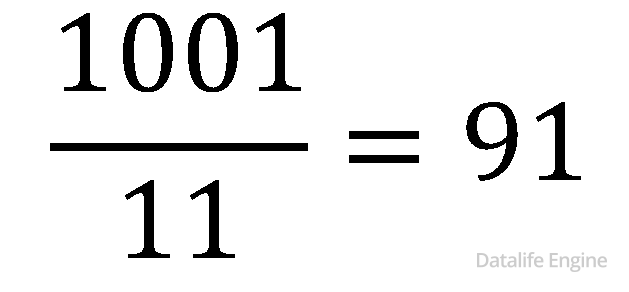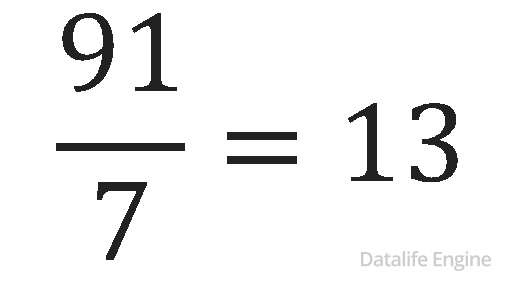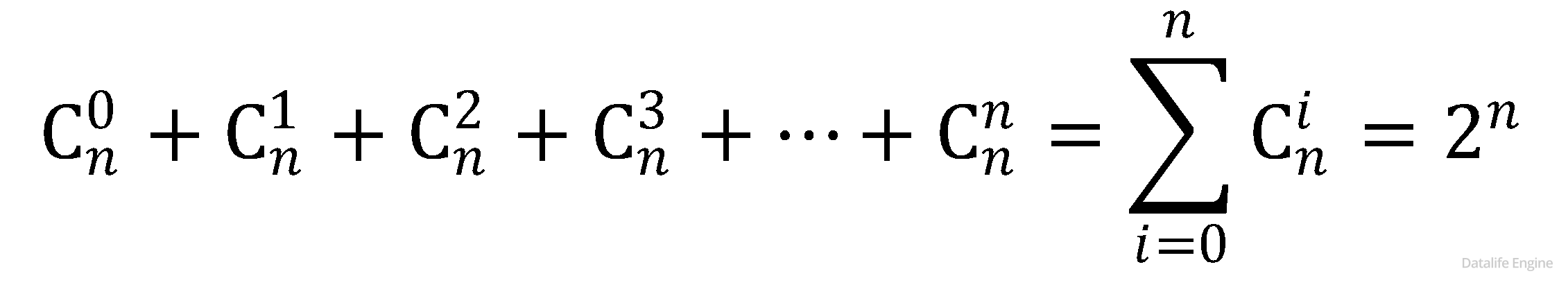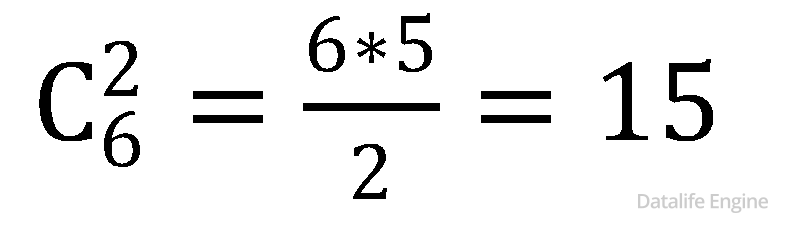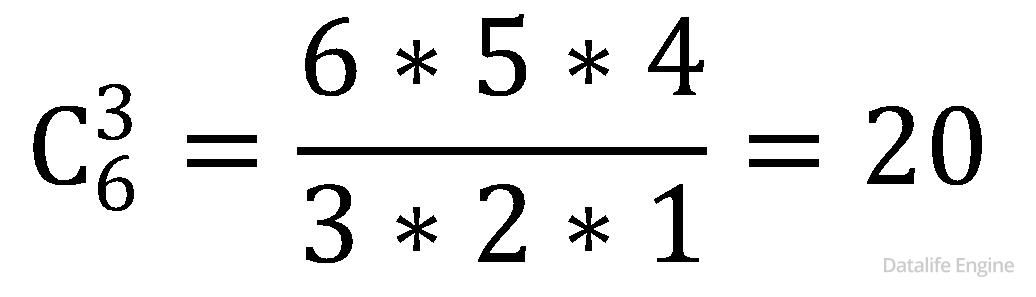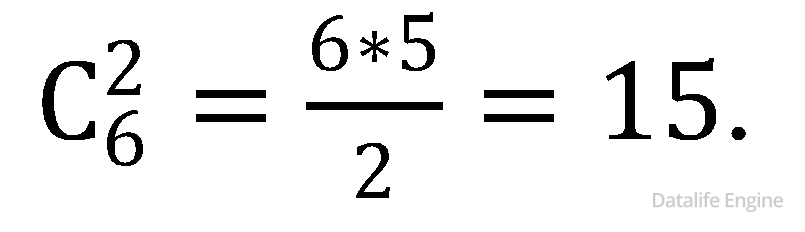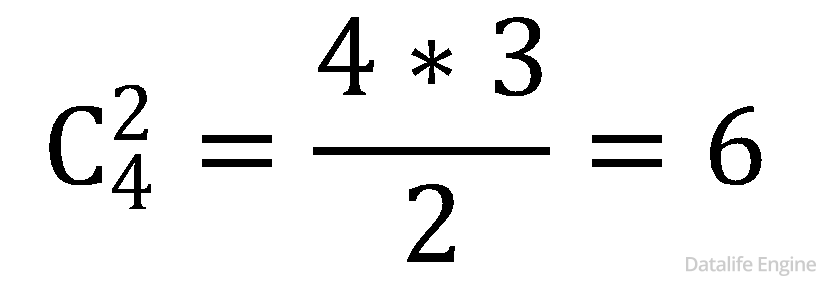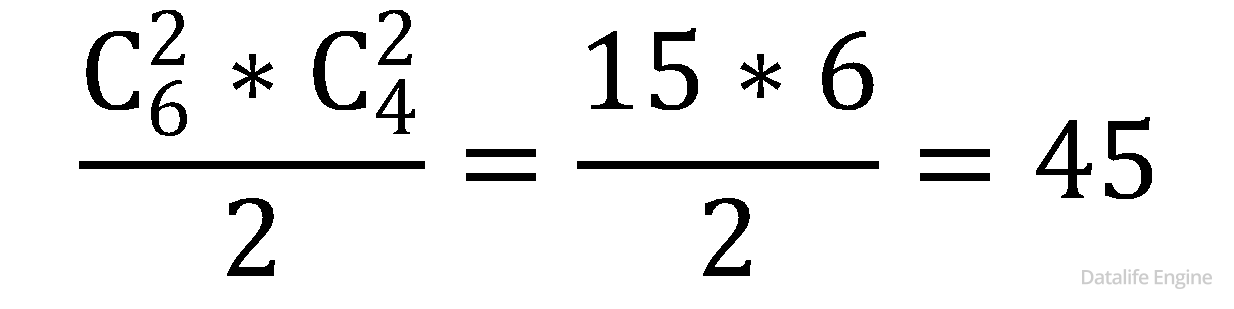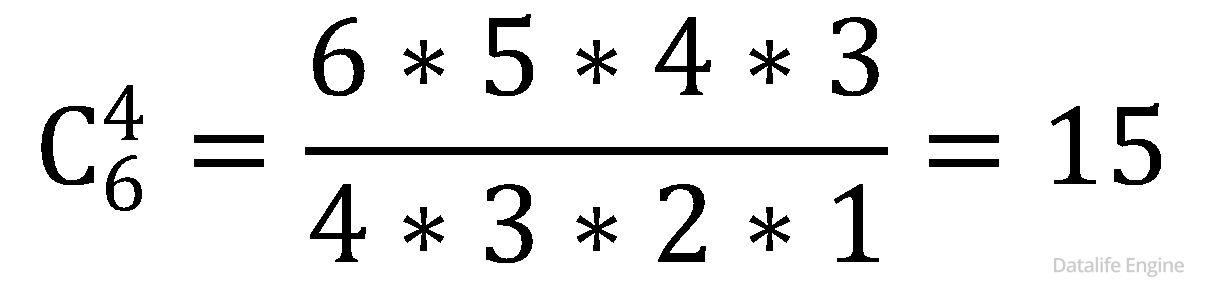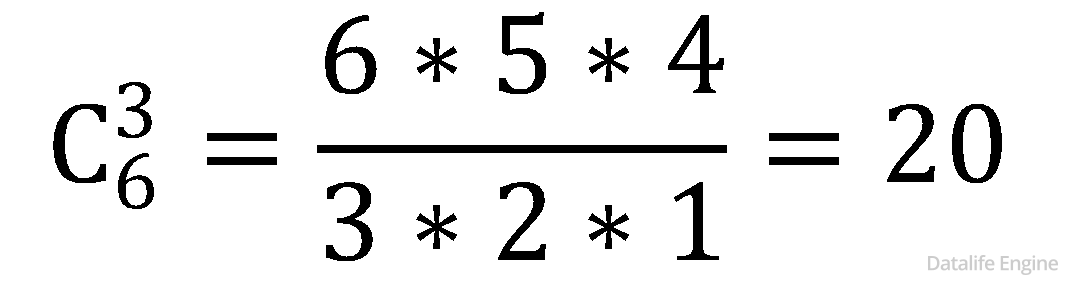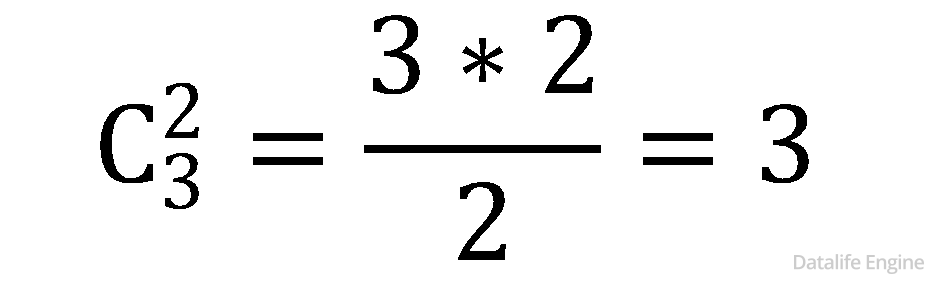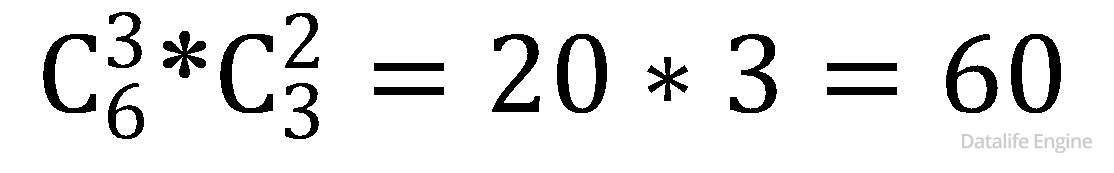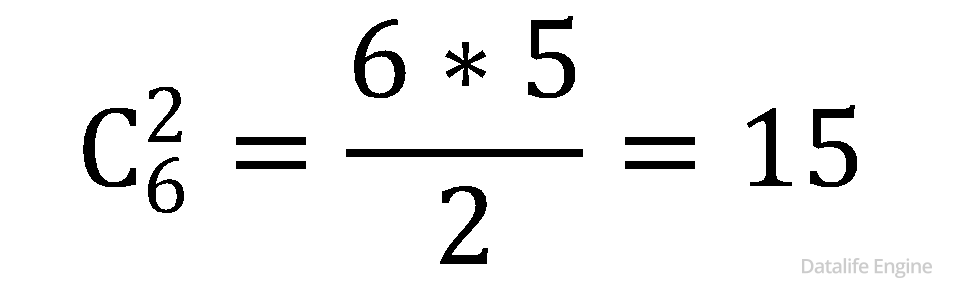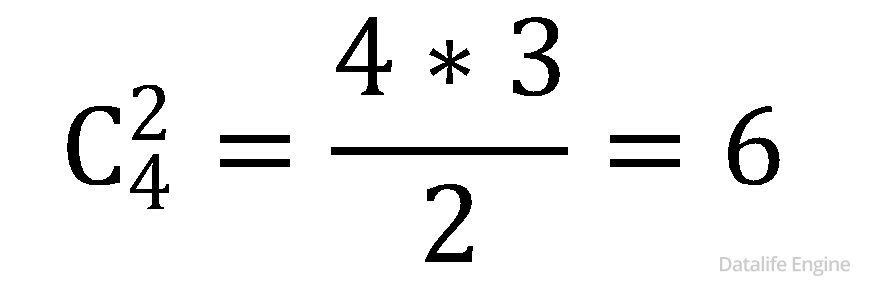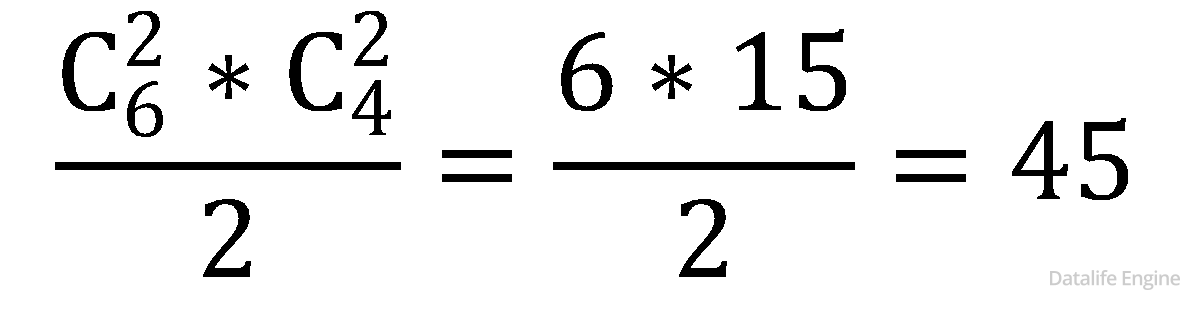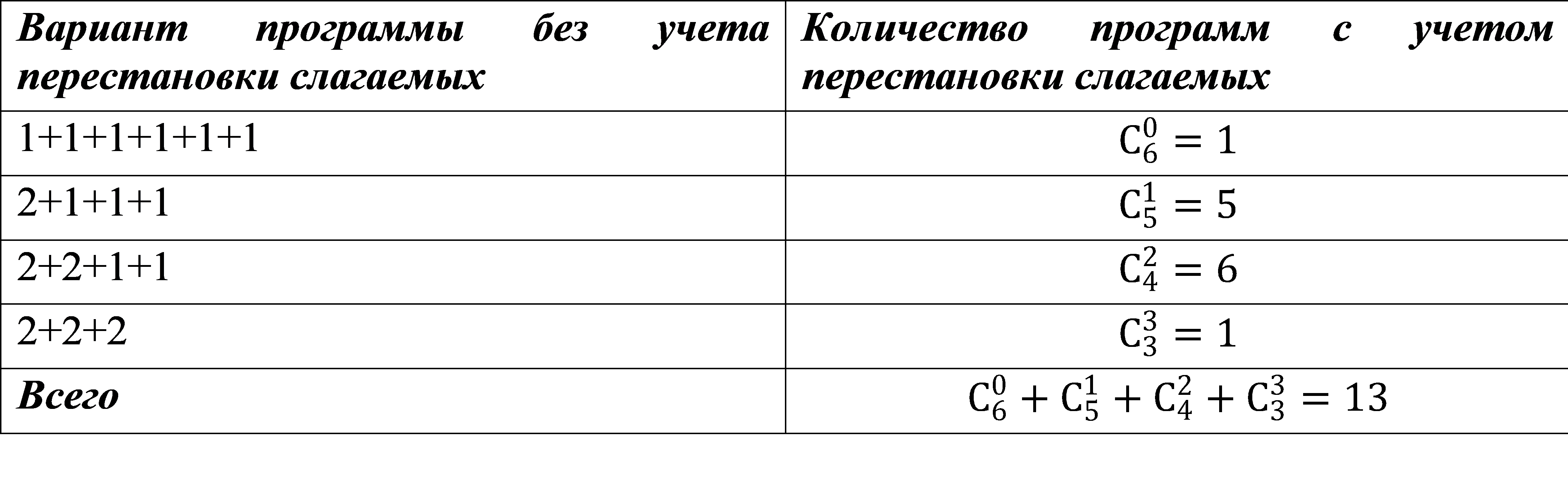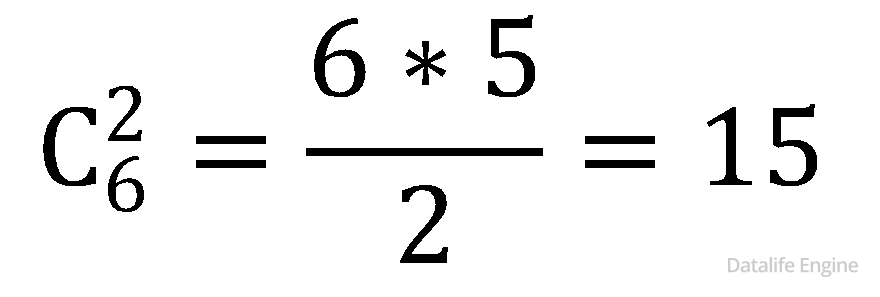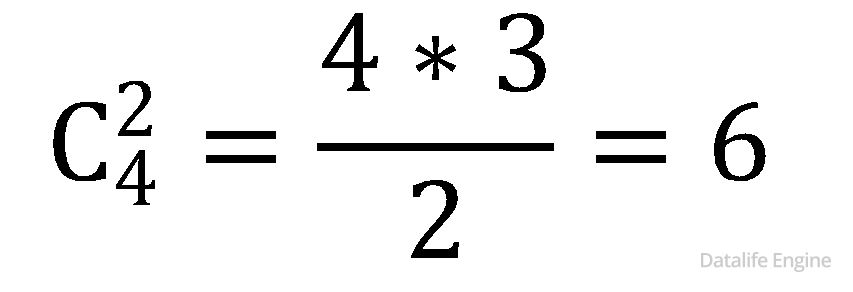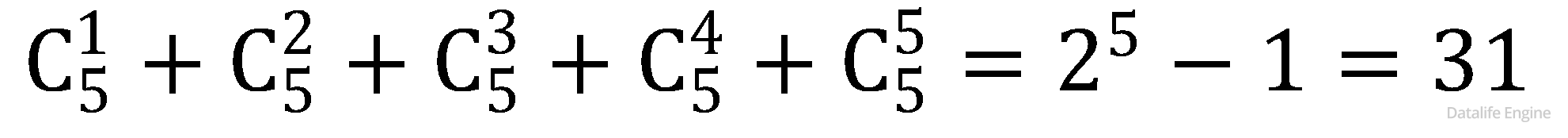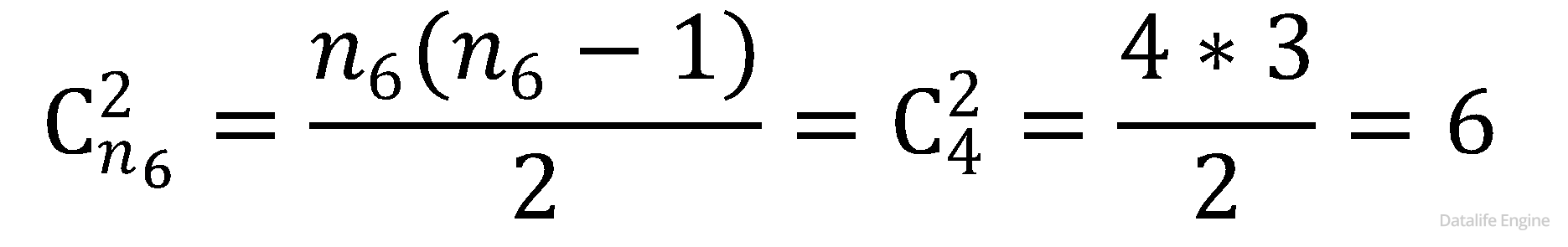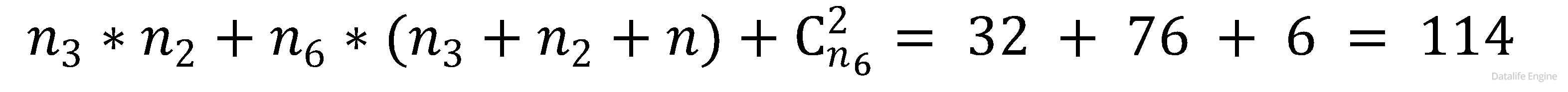Образовательный портал Павла Добряка

Эта задача уже была решена в нашей книге под номером 4.1.5.

Здесь предлагается ответить на два побочных вопроса.

Вопрос №1. Сколько строчек в таблице истинности?

Таблица истинности состоит из четырех колонок. В клетках могут быть записаны 0 или 1 (истина или ложь). Значения в клетках могут повторяться (то есть возможна строка 0000). Это классическая задача на степенную формулу:

Количество строк в таблице истинности с количеством колонок n равно:

2ⁿ = 2⁴ = 16

Ответ №1: 16

 

Вопрос №2. Сколько возможно расположений переменных в таблице истинности?

Рассмотрим шапку таблицы:

???

???

???

???

На первое место мы можем поставить одну из четырех переменных {x, y, z, w}.

На второе место – одну из трех переменных (одна уже была задействована), имена переменных не повторяются.

На третье – одну из двух, и т.д:

Это классическая комбинаторная задача на размещение (если точнее, то на перестановку).

Пусть n = 4 – количество переменных или количество ячеек (в данном случае – одно и то же).

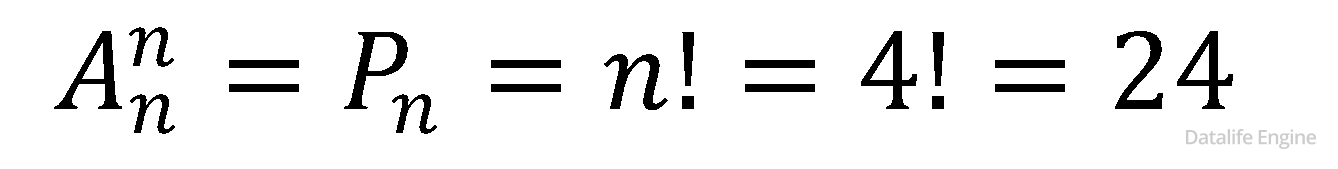
Ответ на этот побочный вопрос позволяет оценить количество вариантов решения, если решать эту задачу из ЕГЭ перебором.

Ответ №2: 24

Определим формулы задач (тип комбинаторной задачи):

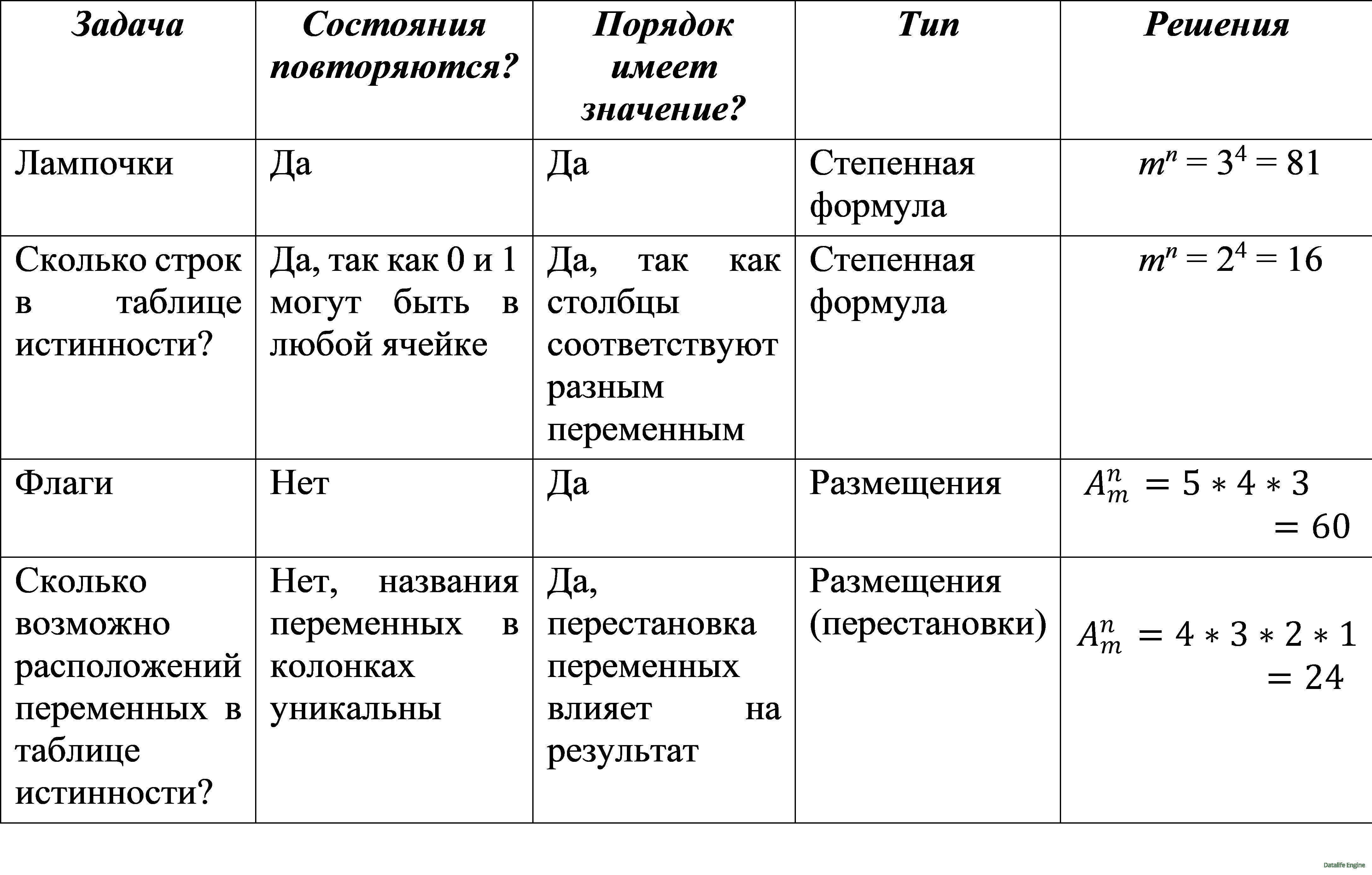Аналогии между задачами:

 Сравним формулу, применяемую для решения задачи.

Задача	Состояния повторяются?	Порядок имеет значение?	Тип	Решения
Лампочки	Да	Да	Степенная формула	mn = 34 = 81
Адреса компьютеров	Да, так как информацию храним в битах. 0 и 1 могут быть в любой ячейке	Да, так как биты пронумерованы (используется позиционная система счисления)	Степенная формула	mn = 213 – 2 = 8192

 

Сравним параметры степенной формулы:

Задача	Мощность алфавита m	Кол-во ячеек n	Кол-во слов I	Формула и решение
Про лампочки	Вкл, выкл, мигает - 3	6 лампочек	Неизвестное кол-во сообщений	I = mn = 36 = 729
Адреса компьютеров	Так как бит содержит 0 или 1, мощность алфавита 2	всего ячеек под нулями маски - 13	Неизвестное количество чисел (адресов)	mn = 213 – 2 = 8192

 

 

Решим теперь несколько новых задач.

Вспомните решение задачи 1.6.3 и воспользуйтесь знаниями комбинаторики (задача на сочетания).

Такой тип задачи на системы счисления мы уже решали – 1.6.3. Он заключается в поиске делителей числа. Пусть n – возможное основание системы счисления.

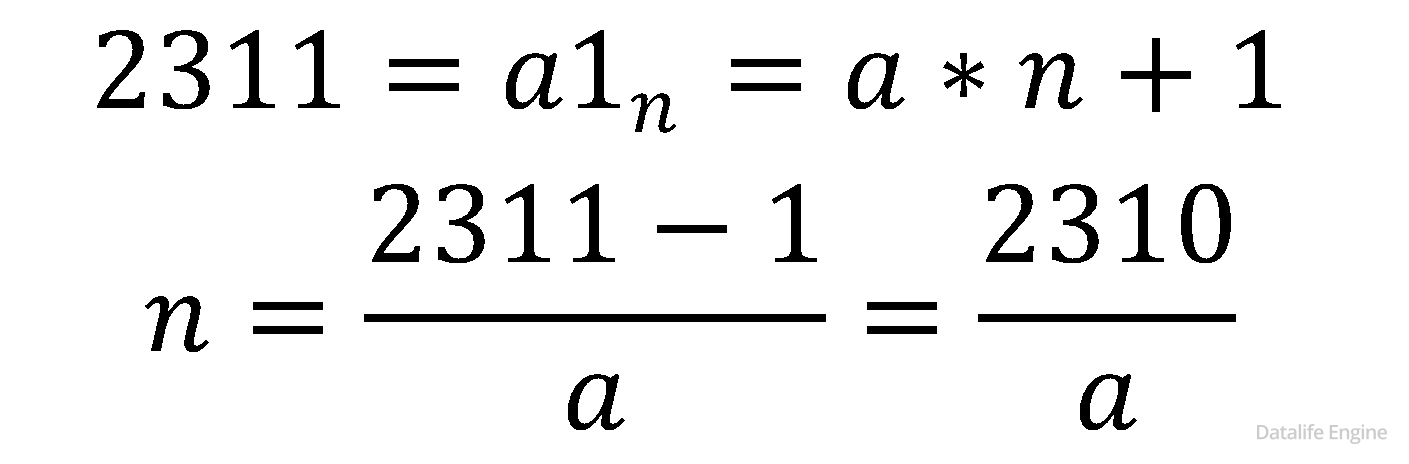
Где натуральное число a > 1.

Таким образом, задача свелась к поиску делителей числа 2310.

Проблема в том, что их очень много. Придется пользоваться знаниями комбинаторики. Разложим число 2310 на простые множители, далее будем комбинировать эти простые множители:

2310 = 2 * 3 * 5 * 7 * 11

Итак, есть пять простых чисел – оснований систем счисления. 

Также искомыми основаниями систем счисления будут все попарные произведения этих чисел. Поскольку от перемены мест множителей произведение не меняется, то пользуемся формулой сочетаний:  

Не будем торопиться вычислять ведь нам понадобятся еще произведения троек чисел   и произведения четверок чисел  

Для их вычисления воспользуемся треугольником Паскаля:

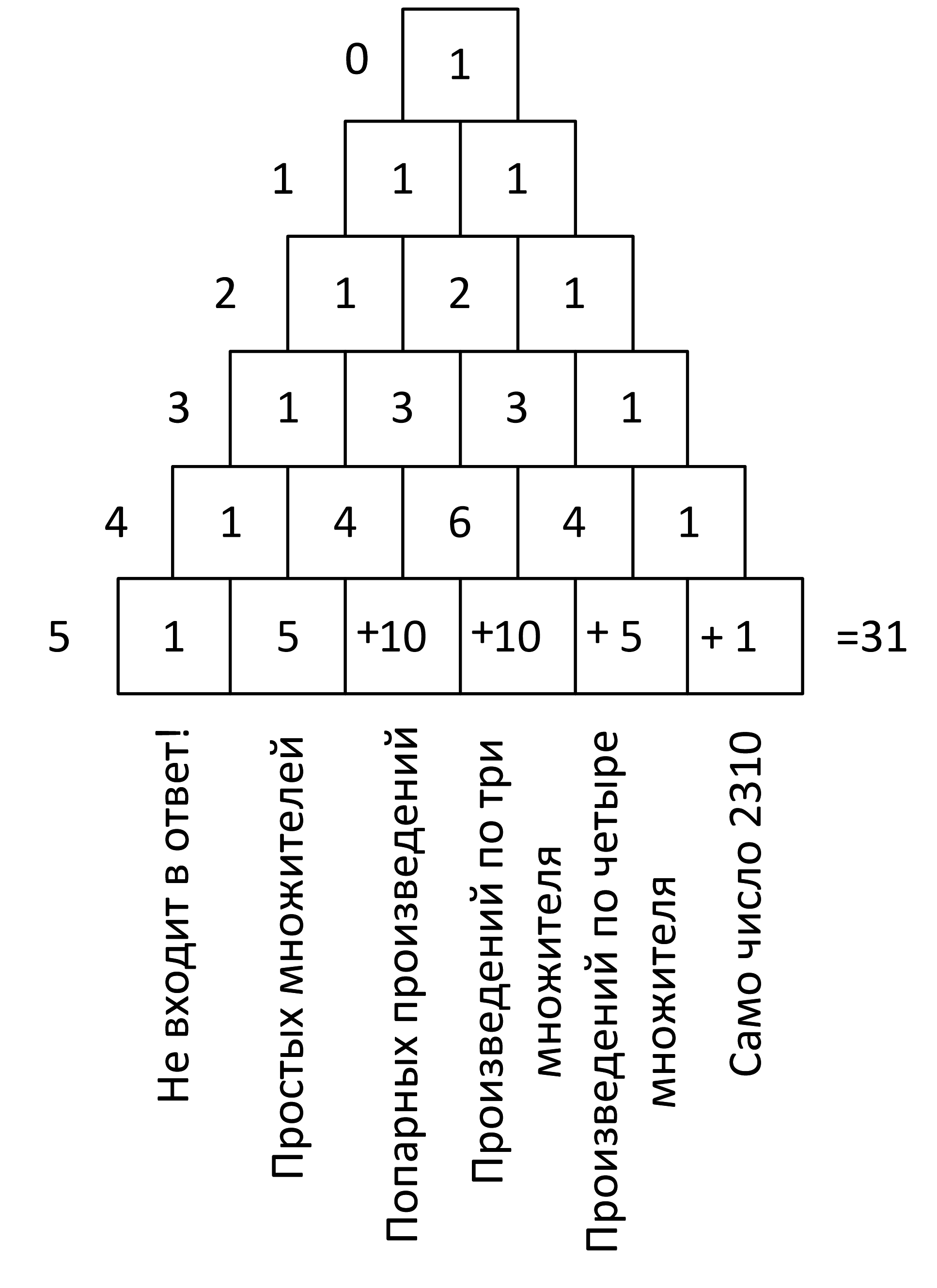
Ответ: 31.

Решайте, как предыдущую задачу. Вспомните признаки делимости чисел из математики.

Итак, нужно разложить на множители число 30030. Воспользуемся признаками делимости:

1. Оно оканчивается на 0, следовательно, делится на 10, то есть на 2 и 5.
2. Сумма цифр равна 6, делится на 3, следовательно, число делится на 3.

Разделим число на найденные делители:

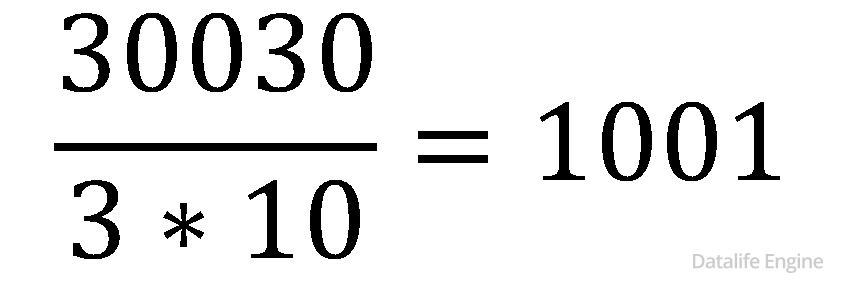
1. Сумма цифр на четных местах 1 + 0 равна сумме чисел на нечетных местах 0 + 1. Следовательно, число делится на 11.

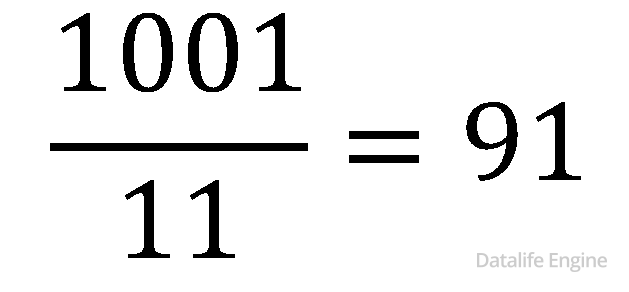
1. Видно, что число 91 делится на 7. Если вы это не видите, то воспользуйтесь свойством: «Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7: 9 – 2 * 1 = 7.

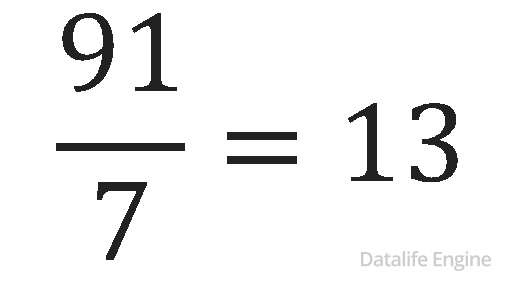
Итак, мы разложили исходное число на простые множители:

30030 = 2 * 3 * 5 * 7 * 11 * 13

Оно состоит из шести множителей. Воспользуемся предыдущей задачей и найдем все произведения из простых множителей по 2, 3, 4, 5 с помощью треугольника Паскаля:

Заметим, что в отличие от задачи D7 мы сложили все числа ряда треугольника Паскаля (ему соответствует 1 – это тоже натуральный делитель числа 30030). Мы получили число, подозрительно напоминающее степень двойки. Для каждого ряда треугольника Паскаля посчитаем его сумму:

Так и есть, сумма ряда в треугольнике Паскаля является степенью двойки. А значит:

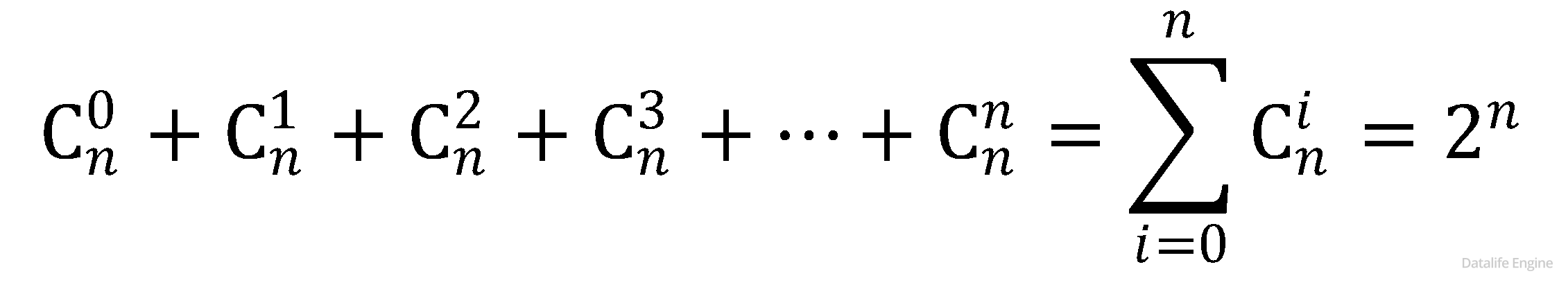
Получается, что количество всех возможных произведений из n чисел равно 2ⁿ и для поиска количества делителей числа достаточно узнать количество его простых делителей n и посчитать 2ⁿ! То есть можно и не работать с формулами сочетаний и треугольником Паскаля!

Ответ: 64.

Посчитать количество разложений числа 30030 на множители (с точностью до перестановки множителей).

 

1) Очевидно, первые два очевидные разложения:

30030 = 1 * 30030 = 30030 * 1

30030 = 2 * 3 * 5 * 7 * 11 * 13

От перестановки мест множителей произведение не меняется, поэтому считаем, что 2 * 3 * 5 * 7 * 11 * 13 и все перестановки его множителей – это одно и то же разложение.

 

2) Перемножим пару чисел из произведения и посчитаем, сколько есть разложений на пять множителей:

(a * b) * (c) * (d) * (e) * (f)

В качестве a мы можем взять 6 чисел, в качестве b – только 5 чисел (одно уже израсходовали на a). От перемены мест результат не изменится (a * b = b * a), поэтому в качестве парного множителя a*b у нас есть 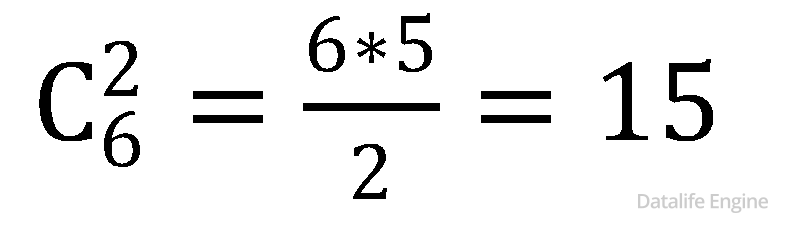  вариантов. Для каждого  из этих 15 вариантов разложение (c) * (d) * (e) * (f) единственное с точностью до перестановки множителей.

 

Для случаев разложения 30030 на четыре множителя у нас появляется два шаблона:

(a*b*c)*(d)*(e)*(f)

(a*b)*(c*d)*(e)*(f)

 

3) Рассмотрим случай, когда у нас есть один тройной множитель. 

(a*b*c)*(d)*(e)*(f)

Аналогично второму пункту количество вариантов равно:   

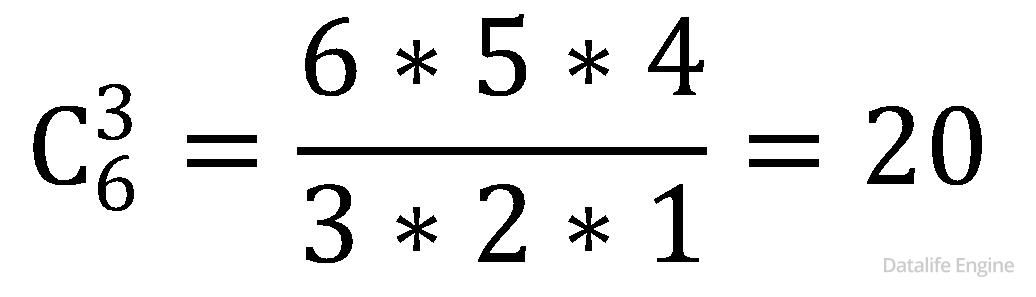
4) Рассмотрим случай, когда у нас есть два двойных множителя:

(a*b)*(c*d)*(e)*(f)

Для первого двойного множителя, как и в пункте 2, у нас есть  

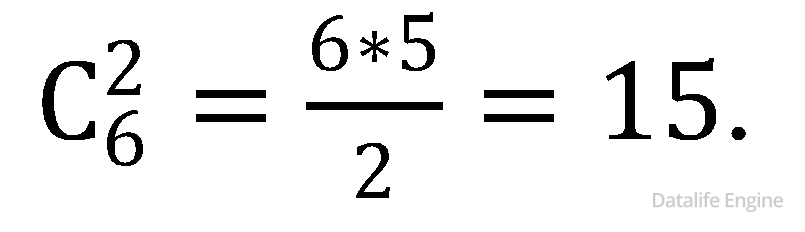
Для второго множителя у нас выбор из 4 простых множителей (2 из 6 исходных простых множителей мы уже израсходовали):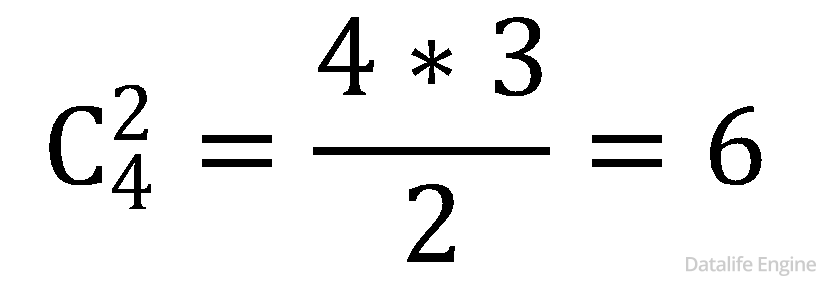  

На остальные одинарные множители у нас остается только один вариант.

Поскольку (a)*(c*) = (с*d)*(a*b), то количество вариантов для этого случая:

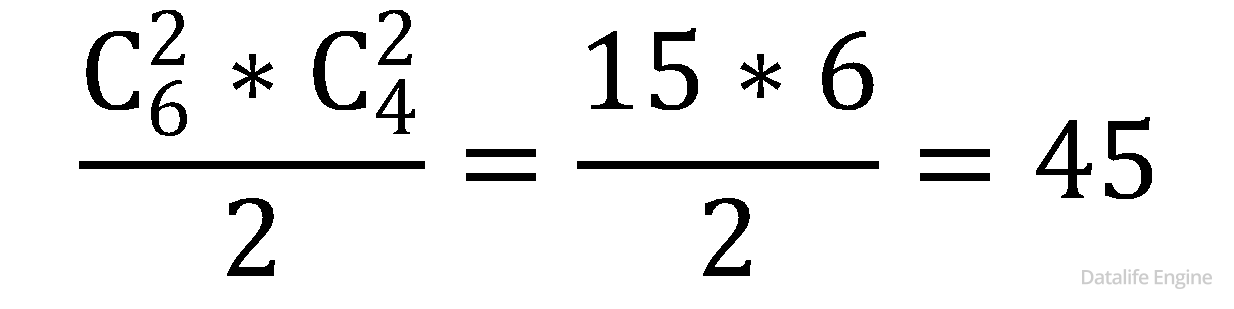
Разложению числа 30030 на три множителя соответствуют случаи:

(a*b*c*d)*(e)*(f)

(a*b*c)*(d*e)*(f)

(a*b)*(c*d)*(e*f)

 

5) Рассмотрим случай

(a*b*c*d)*(e)*(f)

>Количество вариантов четырехсоставного множителя равно  

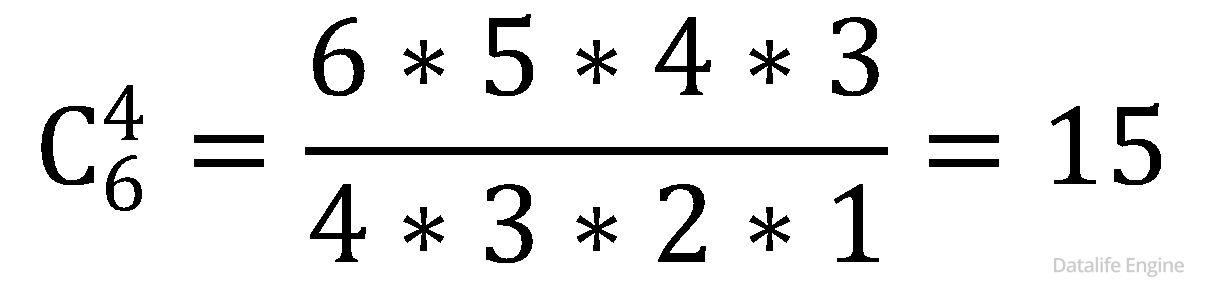
>6) Рассмотрим случай

>(a*b*c)*(d*e)*(f)

Количество вариантов трехсоставного множителя равно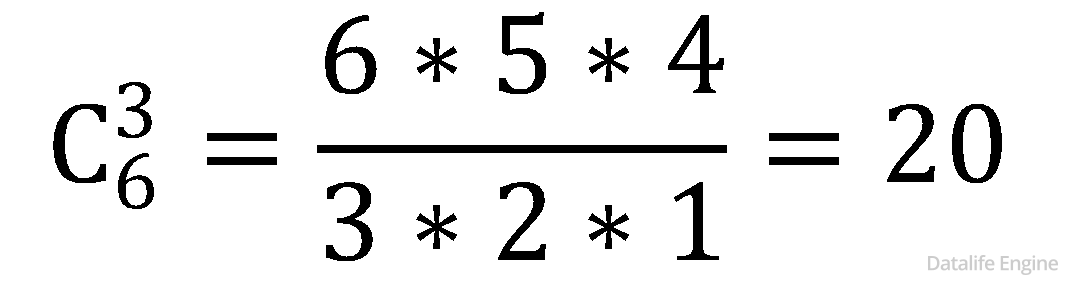 

Количество вариантов двухсоставного множителя (с учетом того, что остался выбор из 3 простых множителей) равно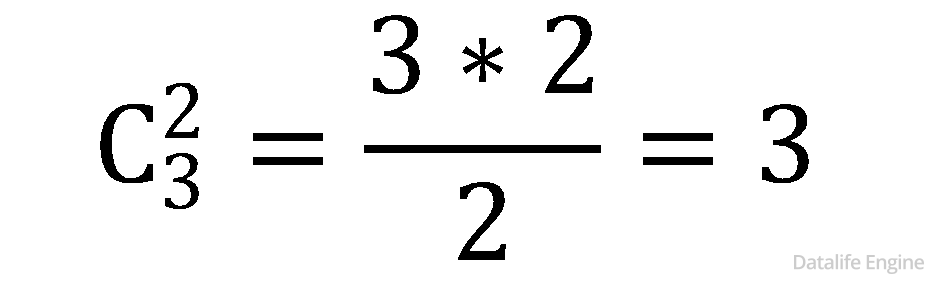  

Всего вариантов: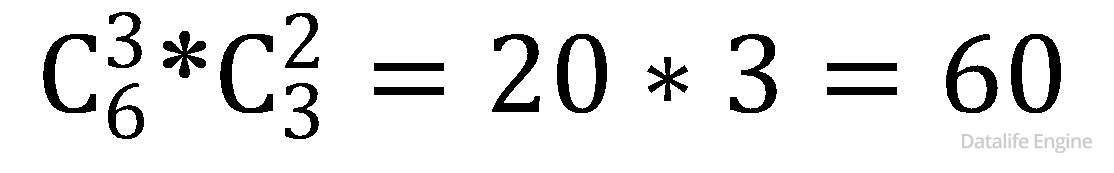  

7) Рассмотрим случай

(a*b)*(c*d)*(e*f)

На первый двойной множитель количество вариантов равно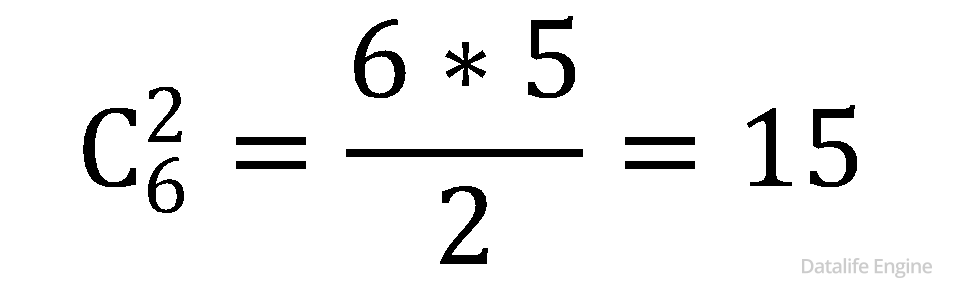  

На второй двойной множитель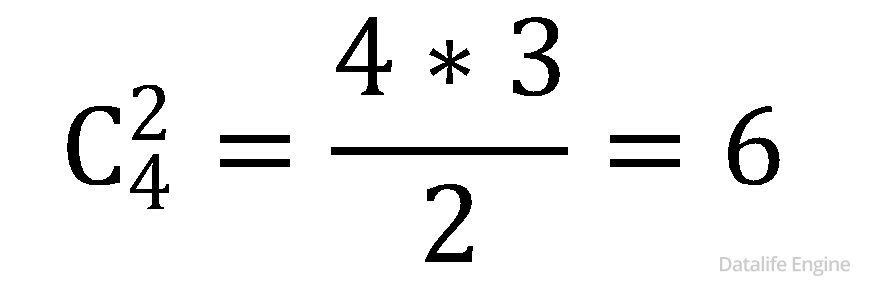 

На третий двойной множитель – 1 вариант.

Всего вариантов: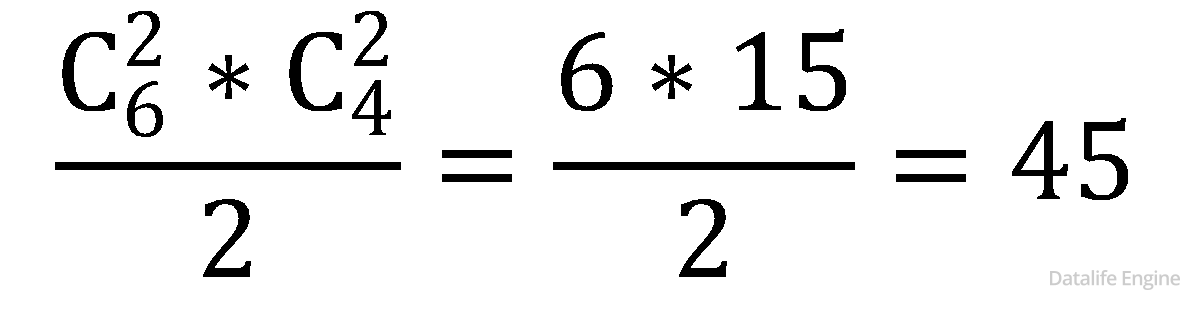  

 

8) Случай, когда у нас два множителя:

(a*b*c*d*e)*f

Проще рассмотреть, сколько есть случаев для f. Это 6 – количество простых множителей. Тогда для составного множителя количество вариантов остается 1.

Осталось сложить результаты:

2 + 15 + 20 + 45 + 15 + 60 + 45 + 6 = 208.

Ответ: 208.

Рассмотрим два способа решения задачи

Комбинаторный способ:

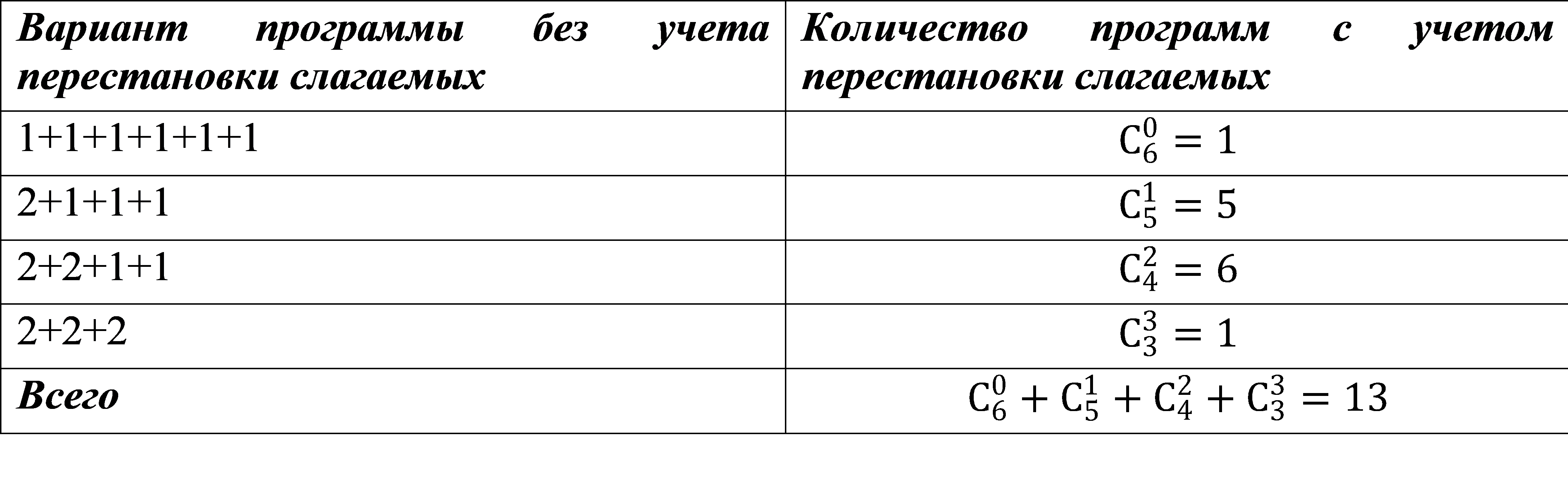
Рекурсивный способ:

R(0)=1

R(1)=R(0)=1

R(2)= R(1)+R(0)=2

R(3)= R(2)+R(1)=3

R(4)= R(3)+R(2)=5

R(5)= R(4)+R(3)=8

R(6)= R(5)+R(4)=13

 

Посмотрим треугольник Паскаля и найдем на нем эти числа:

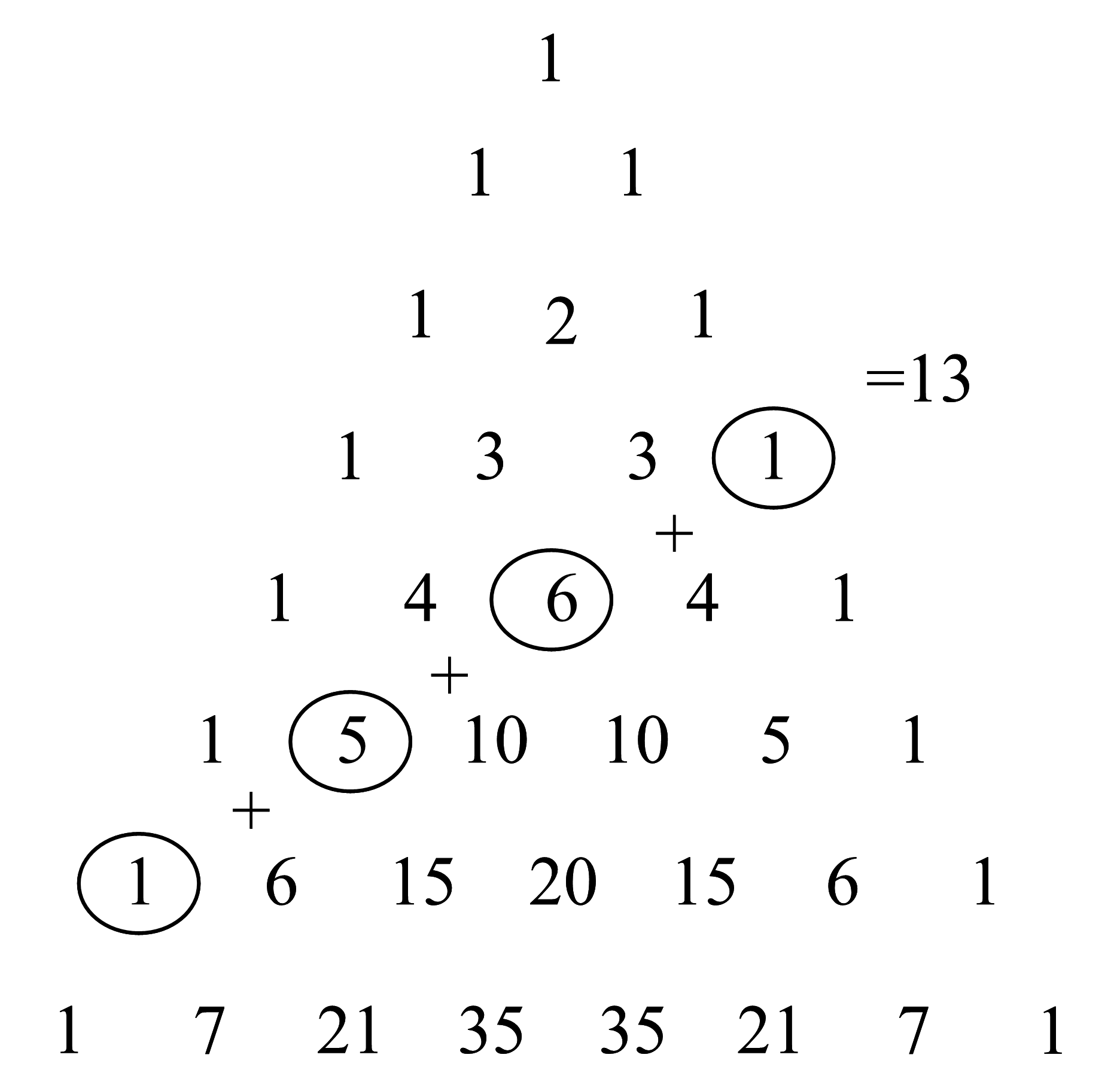
Получается, что сумма чисел в диагонали треугольника Паскаля равна числу Фибоначчи. Проверим это для других диагоналей:

 Обе эти задачи – на использование формулы сочетаний.

Приведем частные случаи вариантов:

1. Задача на алфавит:

A

A

?

?

?

?

Количество размещений буквы А по шести ячейкам определяется по формулам сочетаний: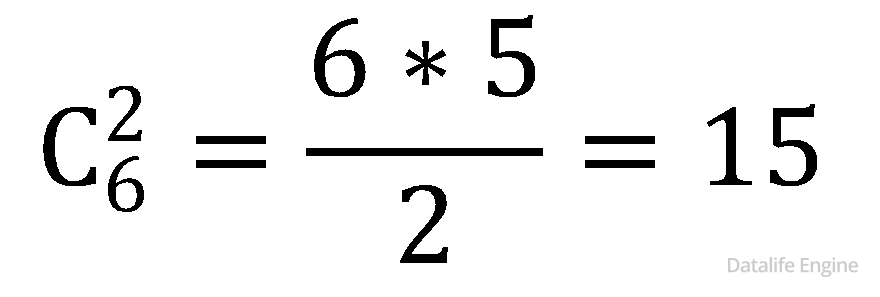 

1. Задача на количество программ

2 + 2 + 1 + 1

 

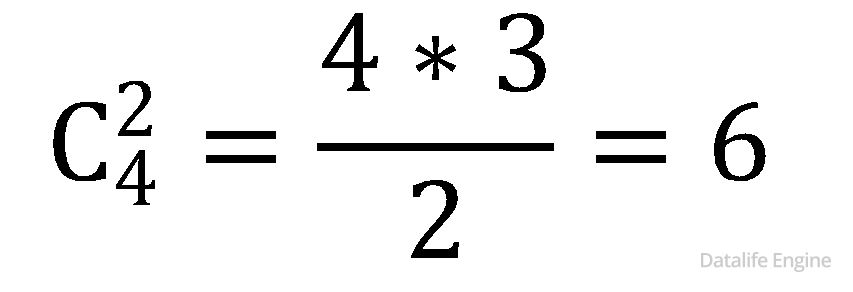
1. Задача на количество систем счисления сводится ко всем возможным комбинациям множителей по одному, два, три, четыре и пять. 

2, 3, 5, 7, 11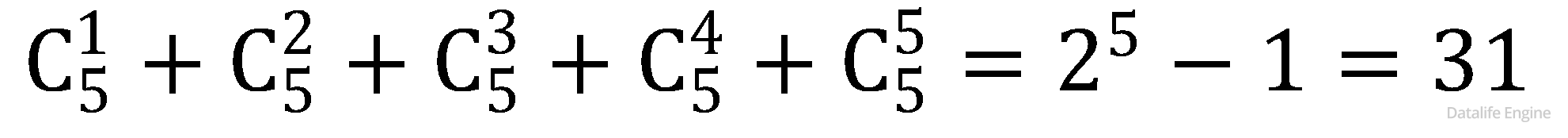

Таким образом, первая и вторая задача идентичны по используемым формулам сочетаний, но во второй задаче меняется количество ячеек, а в первой – нет. Третью задачу можно решить и через сочетания, но гораздо быстрее решить её через степенную формулу, если знать соответствующее свойство треугольника Паскаля.

 

В конце параграфа решим задачу, которая является частью решения последней задачи ЕГЭ по информатике:

Воспользуемся свойством: произведение двух чисел делится на 6, если

1. одно из чисел делится на 6
2. одно из чисел делится на 2, а другое – на 3.

Приведем пример. Пусть вводятся все числа от 2 до 24. Рассортируем их по признакам делимости на 6, 3 и 2 и посчитаем их количество в каждой группе:

Делятся на 6:	6, 12, 18, 24	n6 = 4
Делятся на 3 (и не делятся на 6)	3, 9, 15, 21	n3 = 4
Делятся на 2 (и не делятся на 6)	2, 4, 8, 10, 14, 16, 20, 22	n2 = 8
Не делятся на 6, 3 и 2	5, 7, 11, 13, 17, 19, 23	n = 7

 

1. Берем второе свойство: одно из чисел делится на 2, а другое – на 3.

Количество пар чисел равно

n₃ * n₂ = 4 * 8 = 32

 (каждое из чисел, делящихся на 3, можно помножить на каждое из чисел, делящихся на два).

Первое свойство распадается на два случая:

1. Одно число делится на 6, а другое нет. Тогда, аналогично пункту 1, количество пар равно 

n₆ * (n₃ + n₂ + n) = 4 * (4 + 8 + 7) = 76

1. Оба числа делятся на 6. Выбирая одно из них, мы уменьшаем выбор для второго числа. С учетом того, что пары (6,12) и (12,6) считаются идентичными, пользуемся формулой сочетаний:

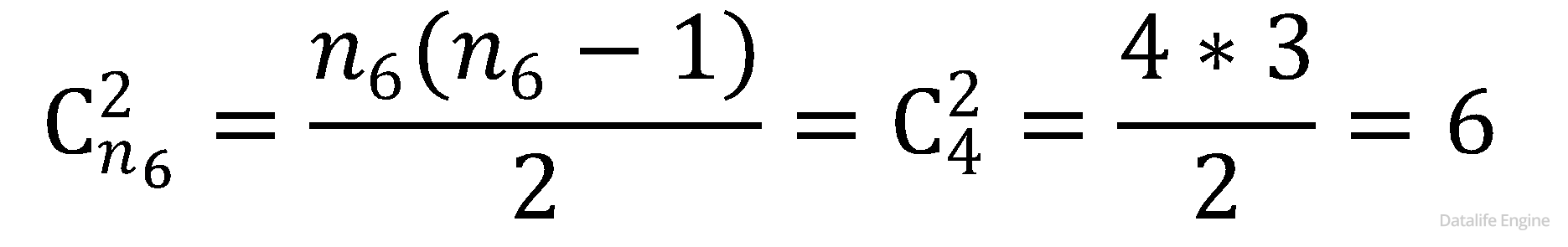
Итак, общее число пар, делящихся на 6, равно:

 

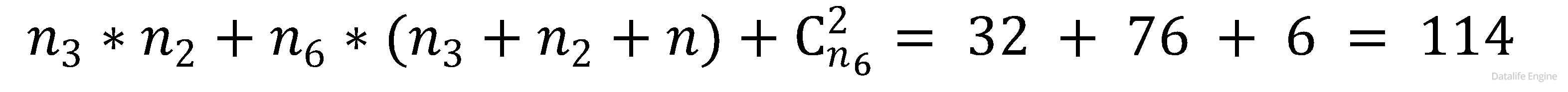
Ответ: 114