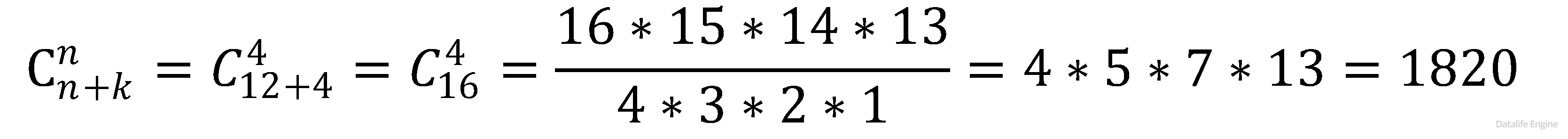Применяется комбинаторика и при решении логических уравнений. В этом параграфе мы для разминки вспомним несколько уже решенных или аналогичных решенным задач на логические уравнения, затем решим усложненные модификации уравнений.
Задание 7.4.1. Решите уравнения из следующей таблицы (если не сможете их решить, сперва посмотрите их аналоги в параграфе «4.5. Логические уравнения»). В чем состоит их комбинаторная суть?

Решим задачи из таблицы:
Задача 7.4.2. Сколько есть решений в логическом уравнении:
A ∨ ⌐B ∨ ⌐C ∨ D = 1?
В уравнении можно определить количество строк в таблице истинности с помощью степенной формулы: 24 = 16. Это не так много. Поскольку переменные соединены с помощью логического «или», проще ответить на вопрос, сколько строчек в таблице истинности дадут ложь. Ответ – всего одна. Значит, количество строчек, дающих истину, равно 16 – 1 = 15.
Ответ: 15
Задача 7.4.3. Сколько есть решений в логическом уравнении:
(X ∨ Y ∨ Z) ∧ (A ∨ ⌐B ∨ ⌐C ∨ D) ∧ (N ∨ ⌐N) = 1
Задача является усложнением задачи 7.4.2. Уравнение состоит из «множителей» соединенных логическим «и». Следовательно, каждый множитель должен принимать значение «истина»:
X ∨ Y ∨ Z = 1
A ∨ ⌐B ∨ ⌐C ∨ D = 1
N ∨ ⌐N = 1
Так же, как и в первой задаче, посчитаем количество решений в каждом из уравнений:
|
Уравнение
|
X ∨ Y ∨ Z = 1
|
A ∨ ⌐B ∨ ⌐C ∨ D = 1
|
N ∨ ⌐N = 1
|
|
Кол-во решений
|
7
|
15
|
2
|
Как на их основе посчитать количество решений? Множители можно уподобить трём ячейкам, а количество решений в них – мощностям алфавитов. Итоговое значение получается перемножением:
|
Уравнение
|
X ∨ Y ∨ Z = 1
|
A ∨ ⌐B ∨ ⌐C ∨ D = 1
|
N ∨ ⌐N = 1
|
Всего:
|
|
Кол-во решений
|
7
|
*
|
15
|
*
|
2
|
= 210
|
|
|
|
|
|
|
|
Ответ: 210.
Задача 7.4.4. Сколько есть решений в логическом уравнении:
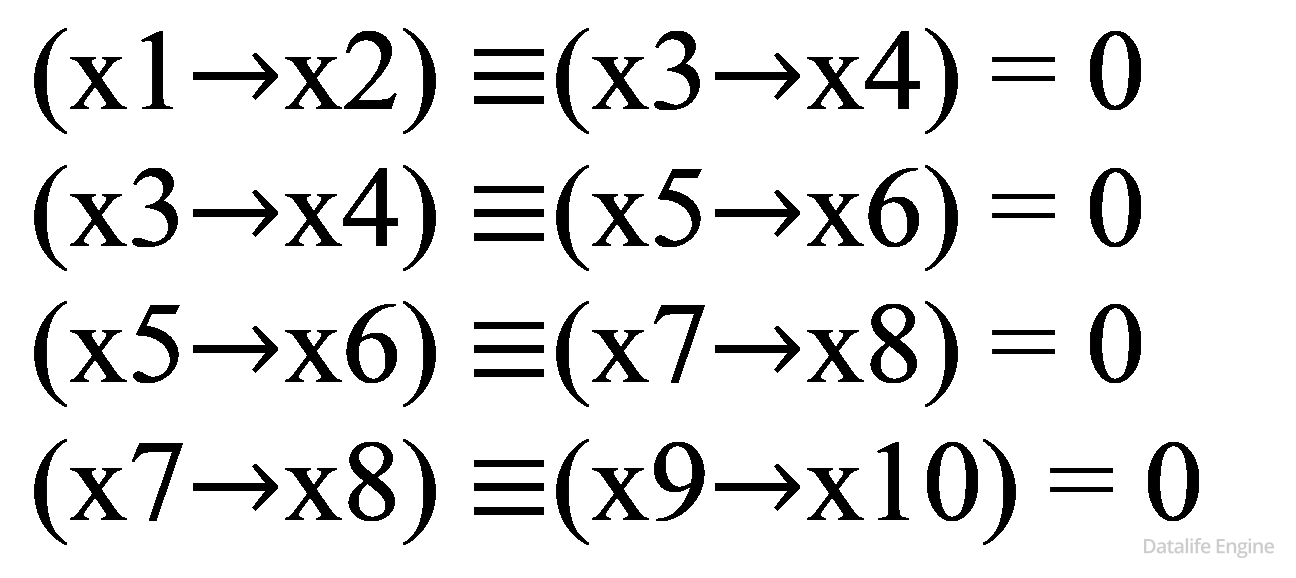
Эта задача похожа на задачу 4.5.4 и решается аналогично. Введем новые обозначения и построим дерево решений:
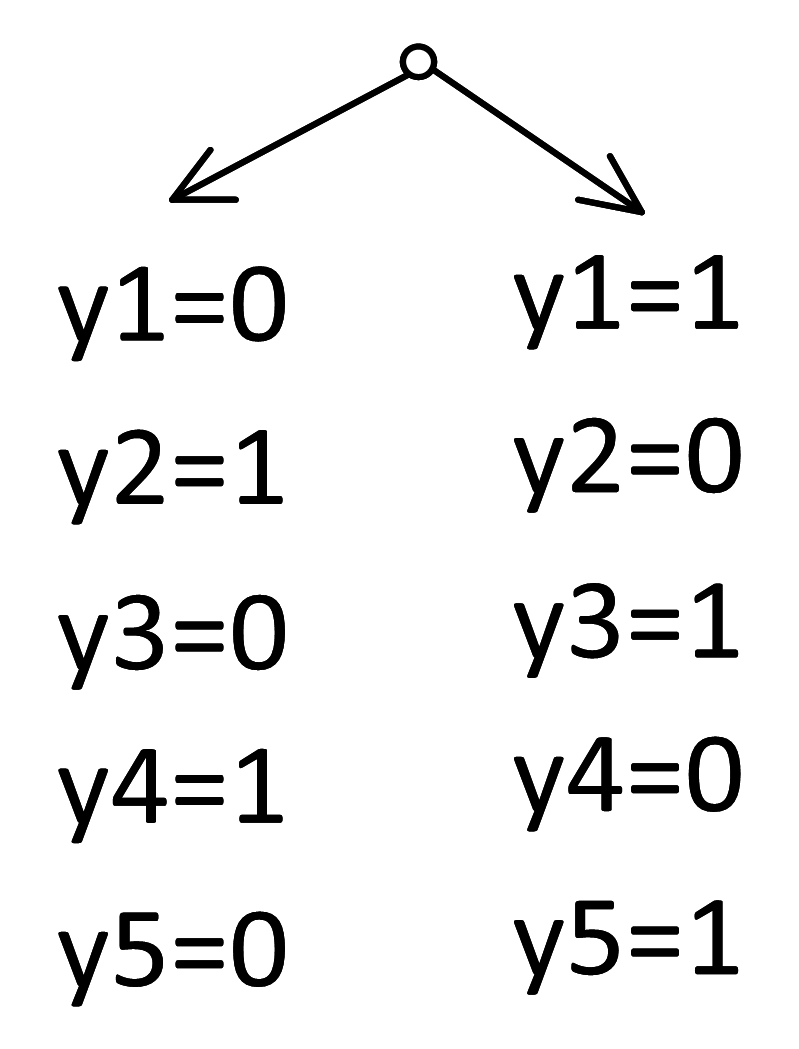
Посмотрим на таблицу истинности для импликации и увидим, что узлам с y = 1 соответствуют три решения по x, а узлам с y = 0 – одно решение. Выпишем количество решений для каждого узла:

Комбинаторная суть задачи заключается в том, что ветку можно уподобить слову из нескольких ячеек, а количество вариантов по x – мощностям алфавитов ячеек:
|
Узлы ветки:
|
y1=0
|
y2=1
|
y3=0
|
y4=1
|
Y5=0
|
Всего
|
|
Мощности алфавитов:
|
1
|
*
|
3
|
*
|
1
|
*
|
3
|
*
|
1
|
*
|
= 9
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитаем обе ветки:

Ответ: 36.
Следующая задача - на построение двух деревьев и соединение их ветвей. Чтобы показать комбинаторную суть соединения деревьев, мы решим эту задачу в двух усложненных вариантах:
Задача 7.4.5. Сколько различных решений имеет система логических уравнений:
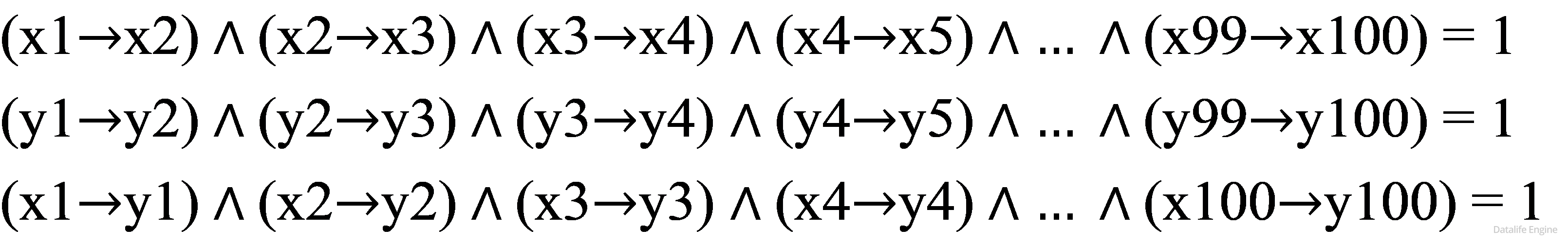
Задача аналогична 4.5.11. Это задача на соединение деревьев и сумму членов арифметической прогрессии.
Решим задачу для фрагмента до x3 и y3. Построим два дерева в виде таблиц, введем обозначения для ветвей, потом свяжем ветви:
|
|
x1
|
0
|
0
|
0
|
1
|
|
x2
|
0
|
0
|
1
|
1
|
|
x3
|
0
|
1
|
1
|
1
|
|
|
A1
|
A2
|
A3
|
A4
|
|
|
y1
|
0
|
0
|
0
|
1
|
|
y2
|
0
|
0
|
1
|
1
|
|
y3
|
0
|
1
|
1
|
1
|
|
|
B1
|
B2
|
B3
|
B4
|
|
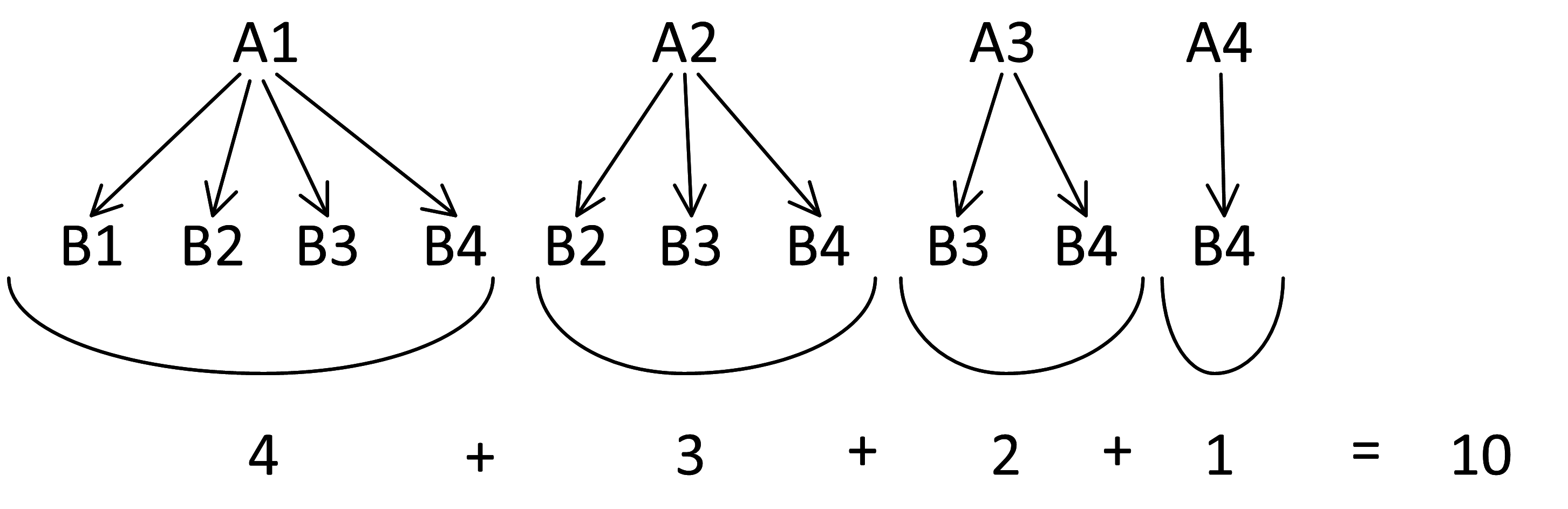
В случае 100 переменных в каждом дереве 101 ветвь. Нам нужно посчитать: 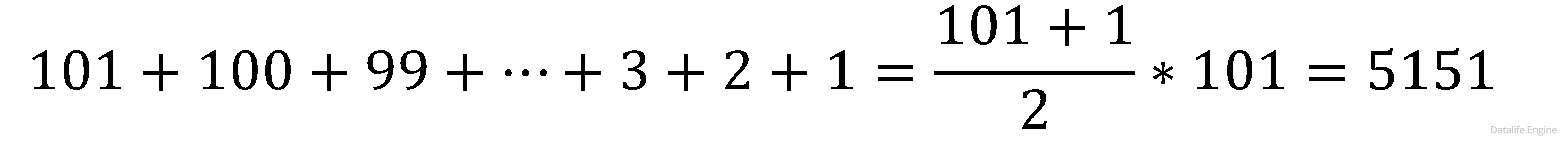
Ответ: 5151.
Задача 7.4.6. Сколько различных решений имеет система логических уравнений:
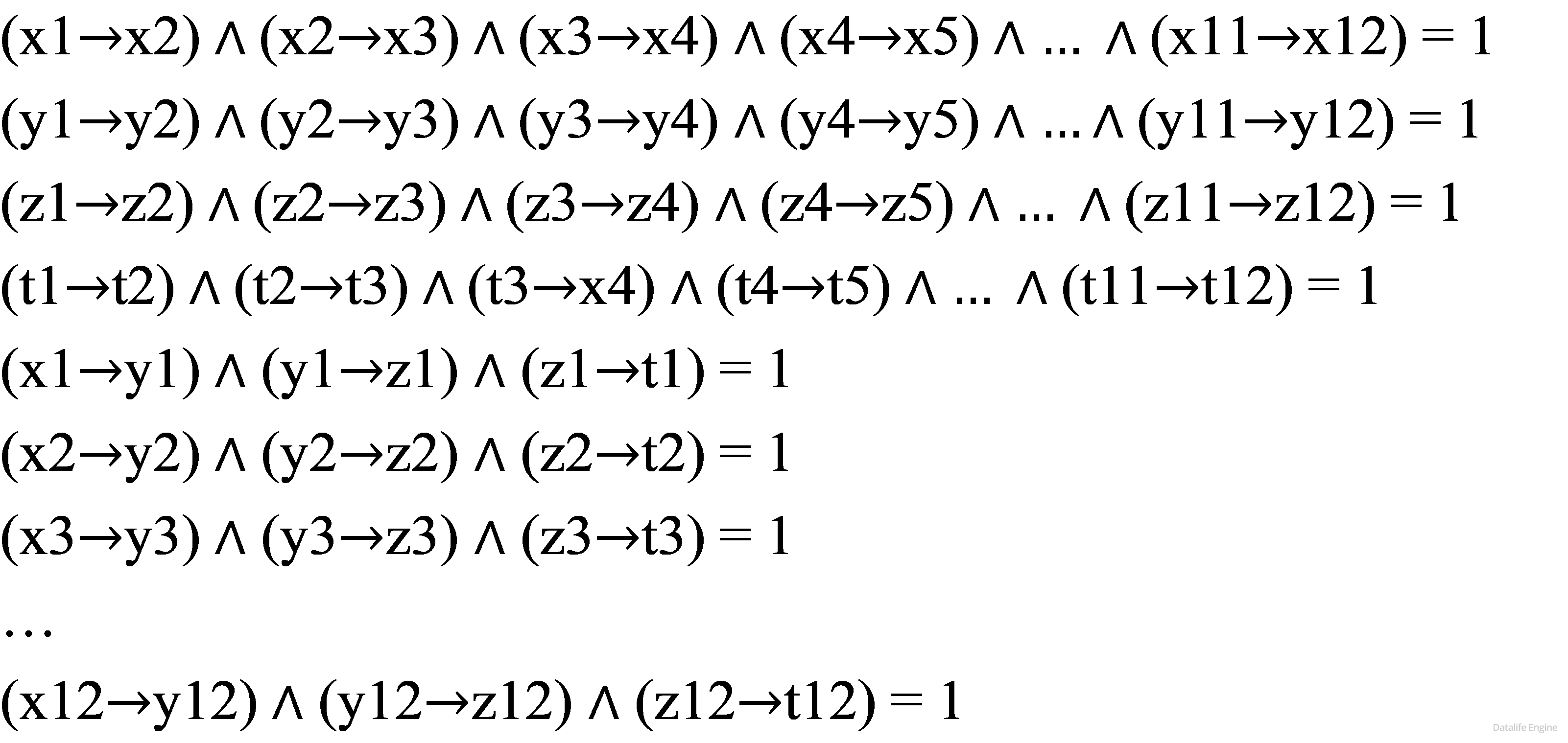
Задача аналогична 4.5.12. Решите для фрагмента, перейдите к формулам комбинаторики.
Решим задачу для фрагмента. Ограничимся тремя переменными x, y, z c индексами от 1 до 3. Построим два дерева в виде таблиц, введем обозначения для ветвей, потом свяжем ветви:
|
|
x1
|
0
|
0
|
0
|
1
|
|
x2
|
0
|
0
|
1
|
1
|
|
x3
|
0
|
1
|
1
|
1
|
|
|
A1
|
A2
|
A3
|
A4
|
|
|
y1
|
0
|
0
|
0
|
1
|
|
y2
|
0
|
0
|
1
|
1
|
|
y3
|
0
|
1
|
1
|
1
|
|
|
B1
|
B2
|
B3
|
B4
|
|
|
z1
|
0
|
0
|
0
|
1
|
|
z2
|
0
|
0
|
1
|
1
|
|
z3
|
0
|
1
|
1
|
1
|
|
|
C1
|
C2
|
C3
|
C4
|
|
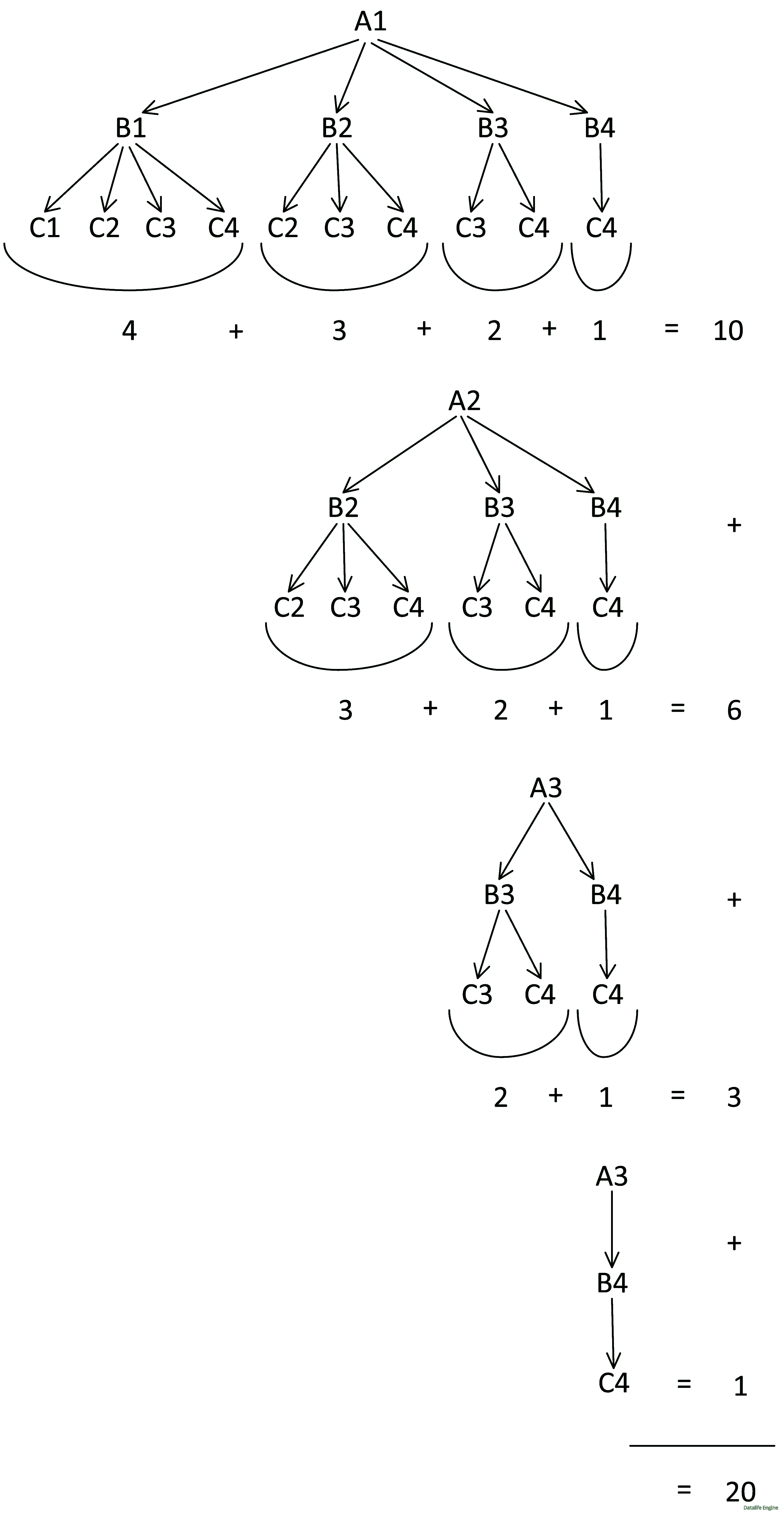
Вспомним, что мы уже находили такого рода суммы в комбинаторной задаче 2.2.4 и 3.2.8. Такие суммы можно посчитать по формуле сочетаний!
Для нашего фрагмента: 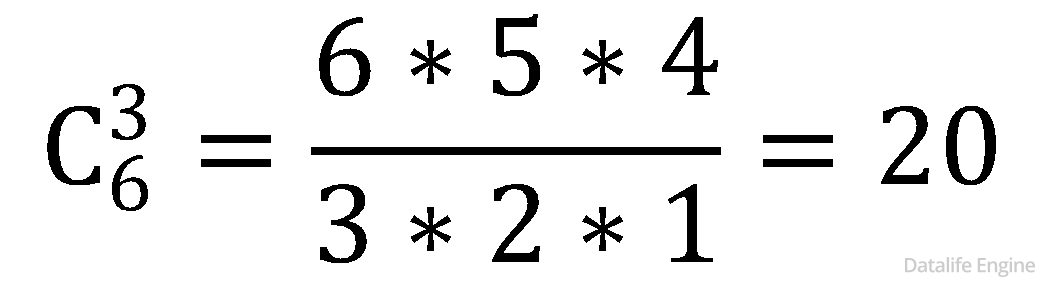
Для предыдущей задачи:
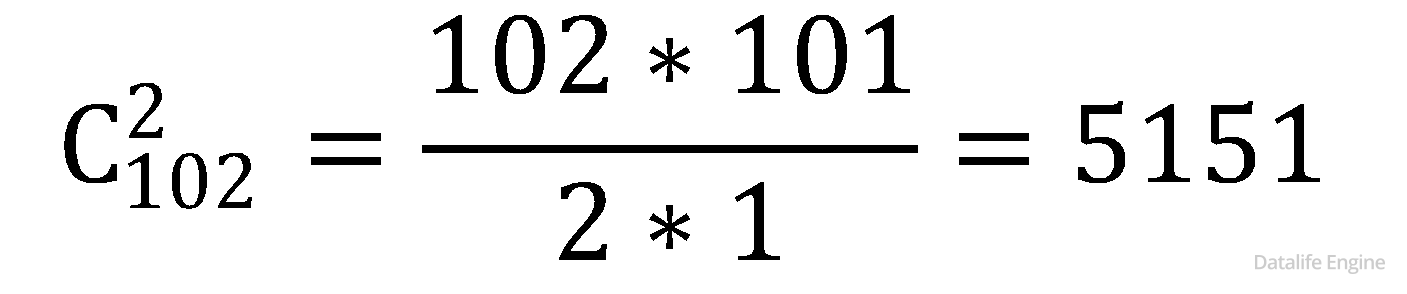
Осталось связать параметры сочетаний с исходными параметрами задачи.
Пусть n – количество групп переменных, а k – количество индексов, тогда количество решений можно посчитать по формуле 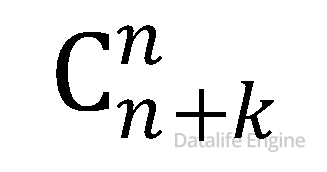 Для нашей задачи количество групп переменных n=4, количество индексов k=10
Для нашей задачи количество групп переменных n=4, количество индексов k=10
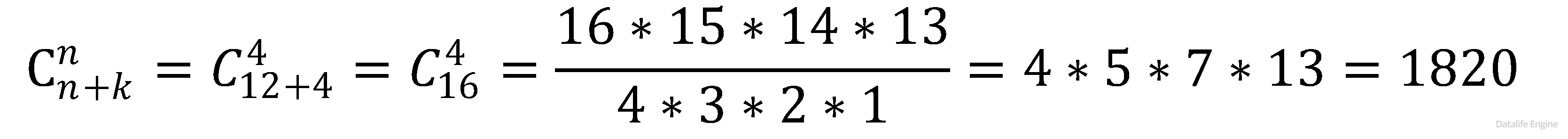
Ответ: 1820.
В этом параграфе мы столкнулись с прогрессиями – последовательностями чисел, получаемых из предыдущих по определенным правилам. Вспомним, что некоторые задачи, например на количество программ, решаются не только комбинаторно, но и рекурсивным методом. В следующем разделе мы подробнее разберем такие задачи из разных разделов ЕГЭ. Поэтому мы еще встретимся и с логическими уравнениями, и с комбинаторикой.

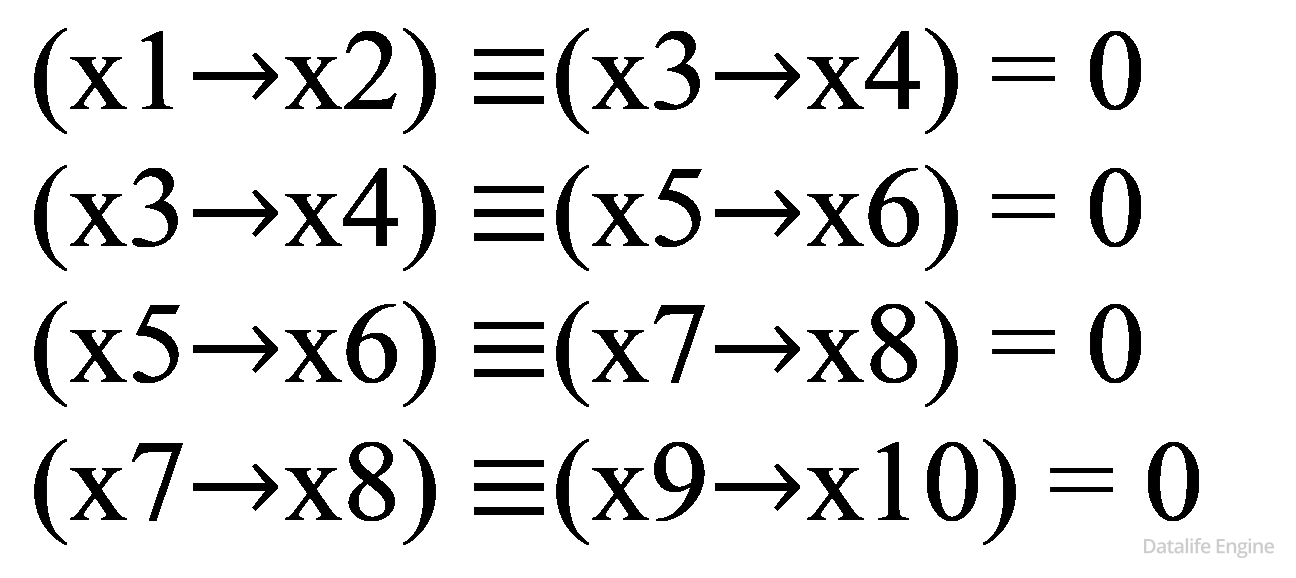
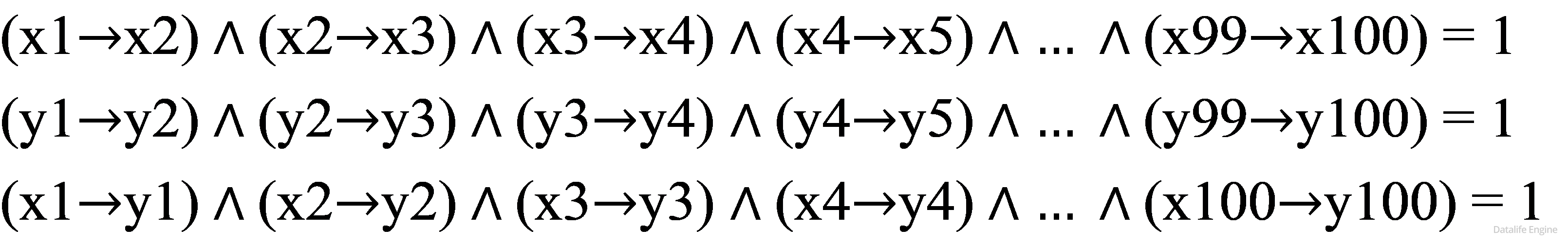
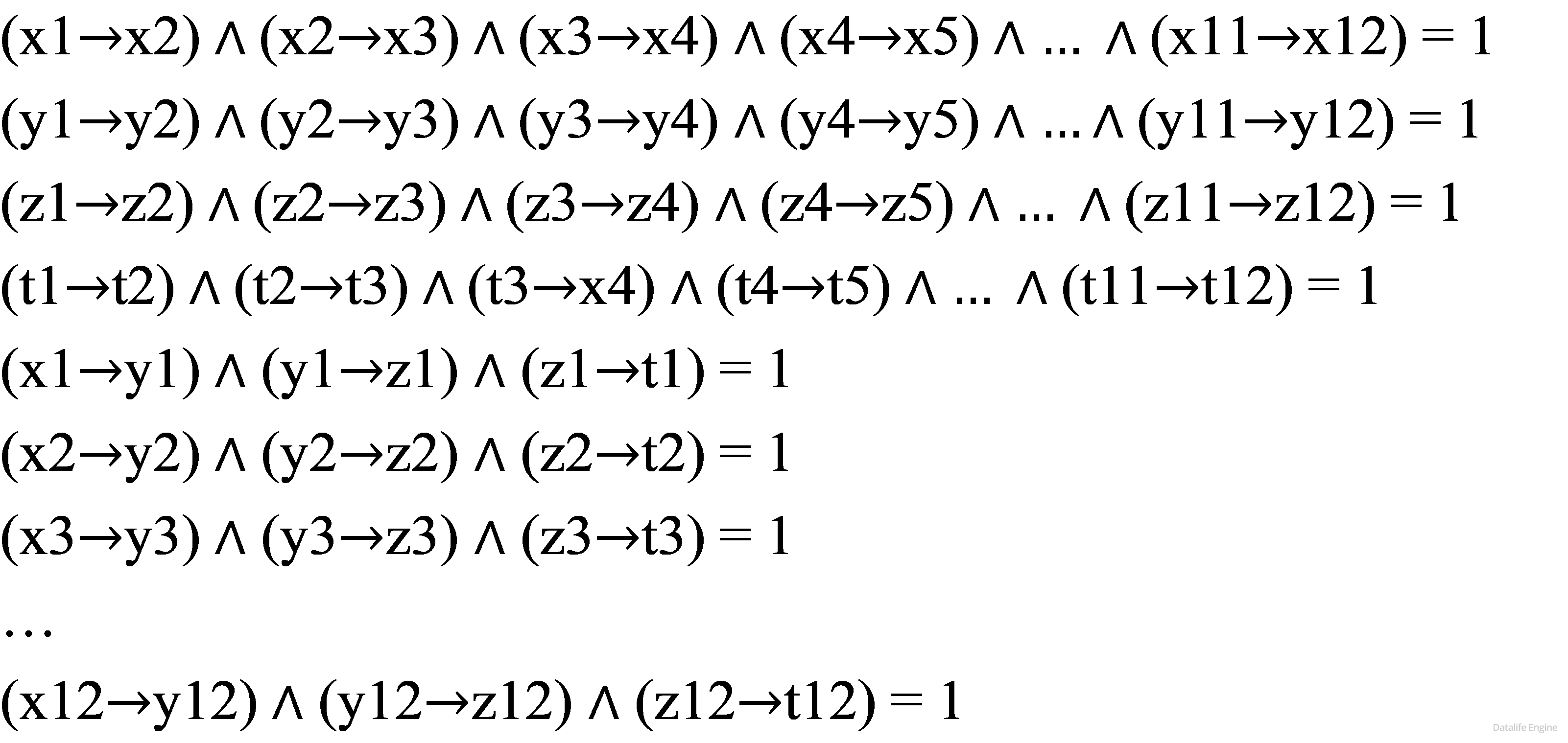





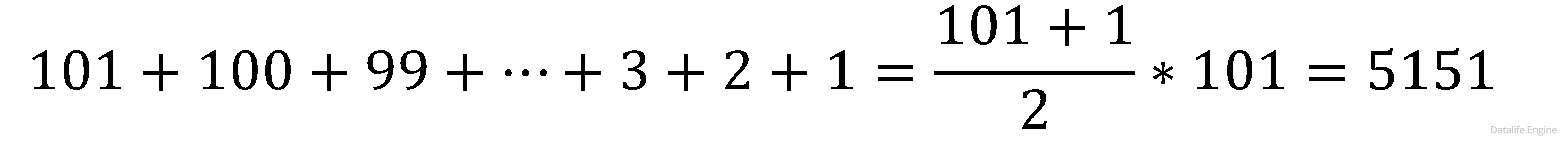

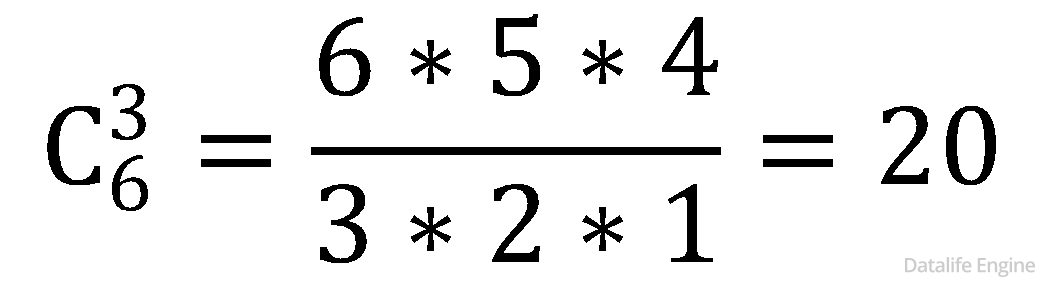
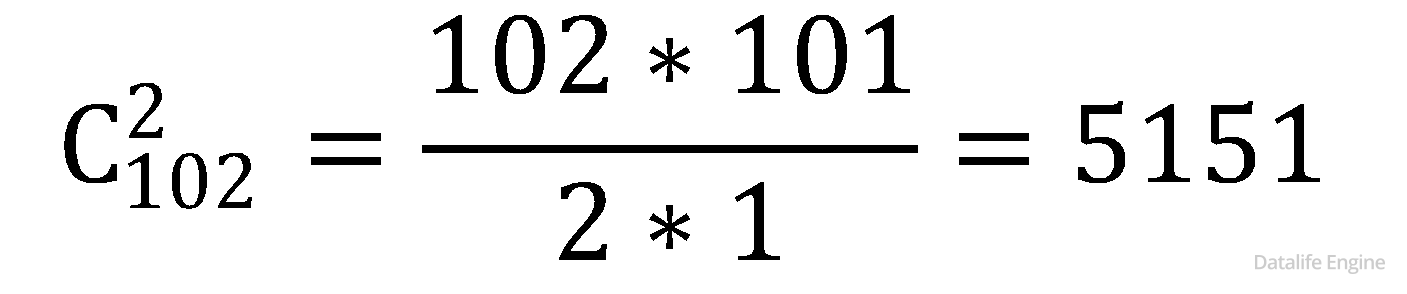
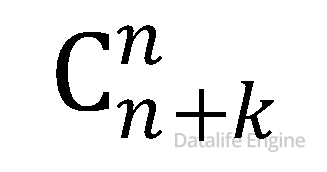 Для нашей задачи количество групп переменных n=4, количество индексов k=10
Для нашей задачи количество групп переменных n=4, количество индексов k=10