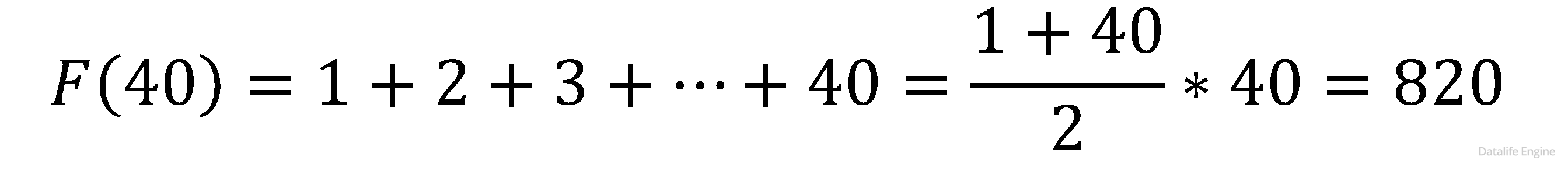В этом параграфе мы познакомимся с еще одной языковой конструкцией – функцией (процедурой). Часто это будут альтернативные алгоритмы к тем программам, которые мы уже изучили (числа Фибоначчи, факториал). В них вместо рекуррентных формул будут рекурсии – функции, которые вызывают сами себя, но уже с другими значениями аргументов.
Задача 8.2.1. Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = F(n – 1) * n, при n >1
Чему равно значение функции F(5)? В ответе запишите только натуральное число.
Задача 8.2.2. Последовательность чисел задается рекуррентным соотношением:
F(1) = 1
F(2) = 1
F(n) = F(n – 2) + F(n – 1), при n >2, где n – натуральное число.
Чему равно восьмое число в последовательности?
В ответе запишите только натуральное число.
Задача 8.2.3. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:
F(1) = 1;
F(n) = F(n − 1) + n, если n > 1
Чему равно значение функции F(40)? В ответе запишите только натуральное число.
Задача 8.2.4. Алгоритм вычисления значения функции F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(1) = 1
F(n) = 2 * G(n – 1) + 5 * n, при n > 1
G(1) = 1
G(n) = F(n – 1) + 2 * n, при n > 1
Чему равно значение функции F(4) + G(4)?
Задача 8.2.5. Последовательность чисел задается рекуррентным соотношением:
F(a,0) = 1
F(a,n) = F(a, n/2) * F(a, n/2), при n > 1, где n – четное натуральное число.
F(a,n) = F(a, n – 1) * a, при n > 1, где n – нечетное натуральное число.
Чему равно пятнадцатое число в последовательности при а = 2?
В ответе запишите только натуральное число.
Задача 8.2.6. Последовательность чисел задается рекуррентным соотношением:
F(a,0) = 1
F(a,n) = F(a*a, n/2), при n > 1, где n – четное натуральное число.
(a,n) = F(a, n – 1) * a, при n > 1, где n – нечетное натуральное число.
Чему равно шестое число в последовательности при а = 3?
В ответе запишите только натуральное число.
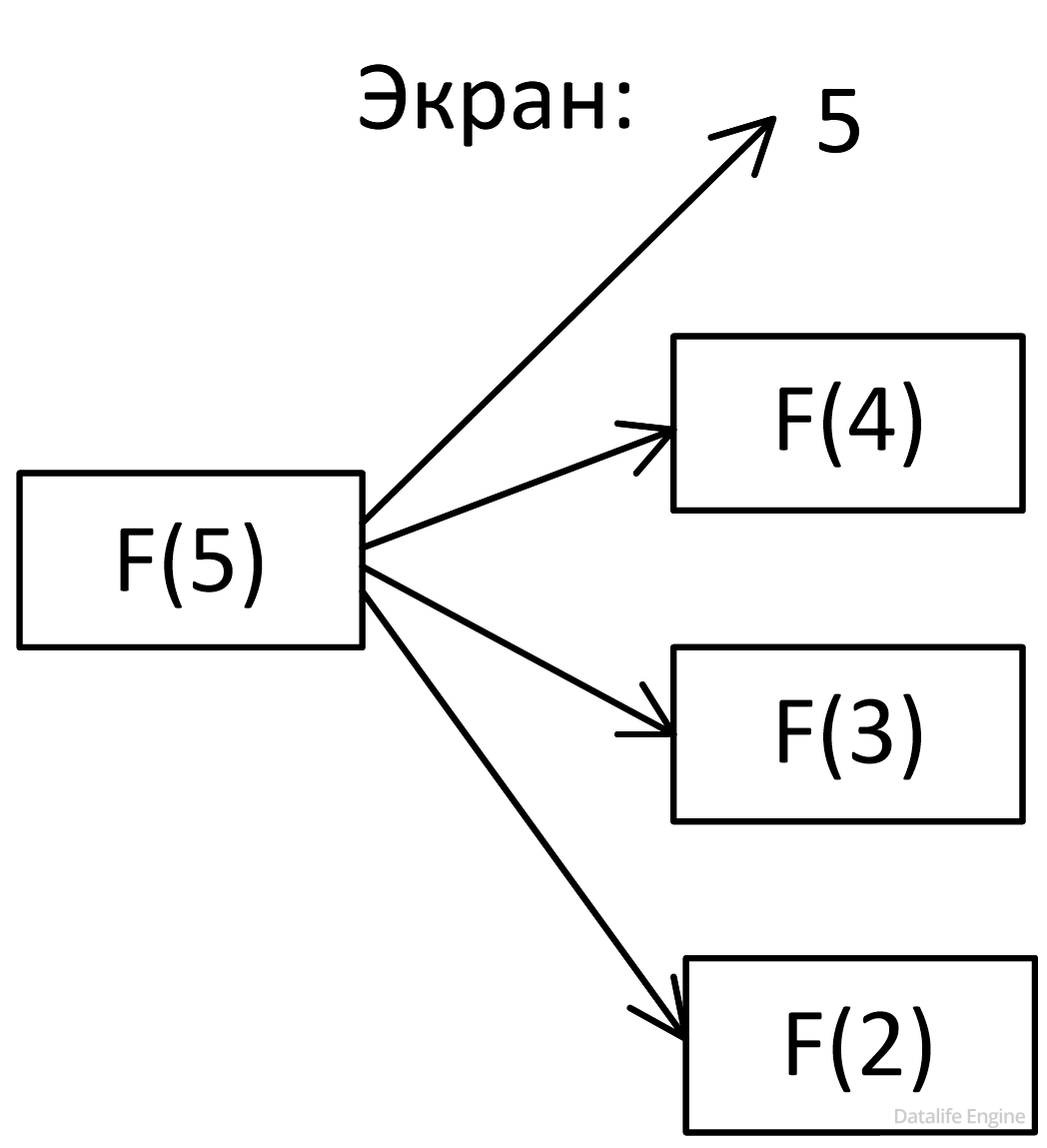
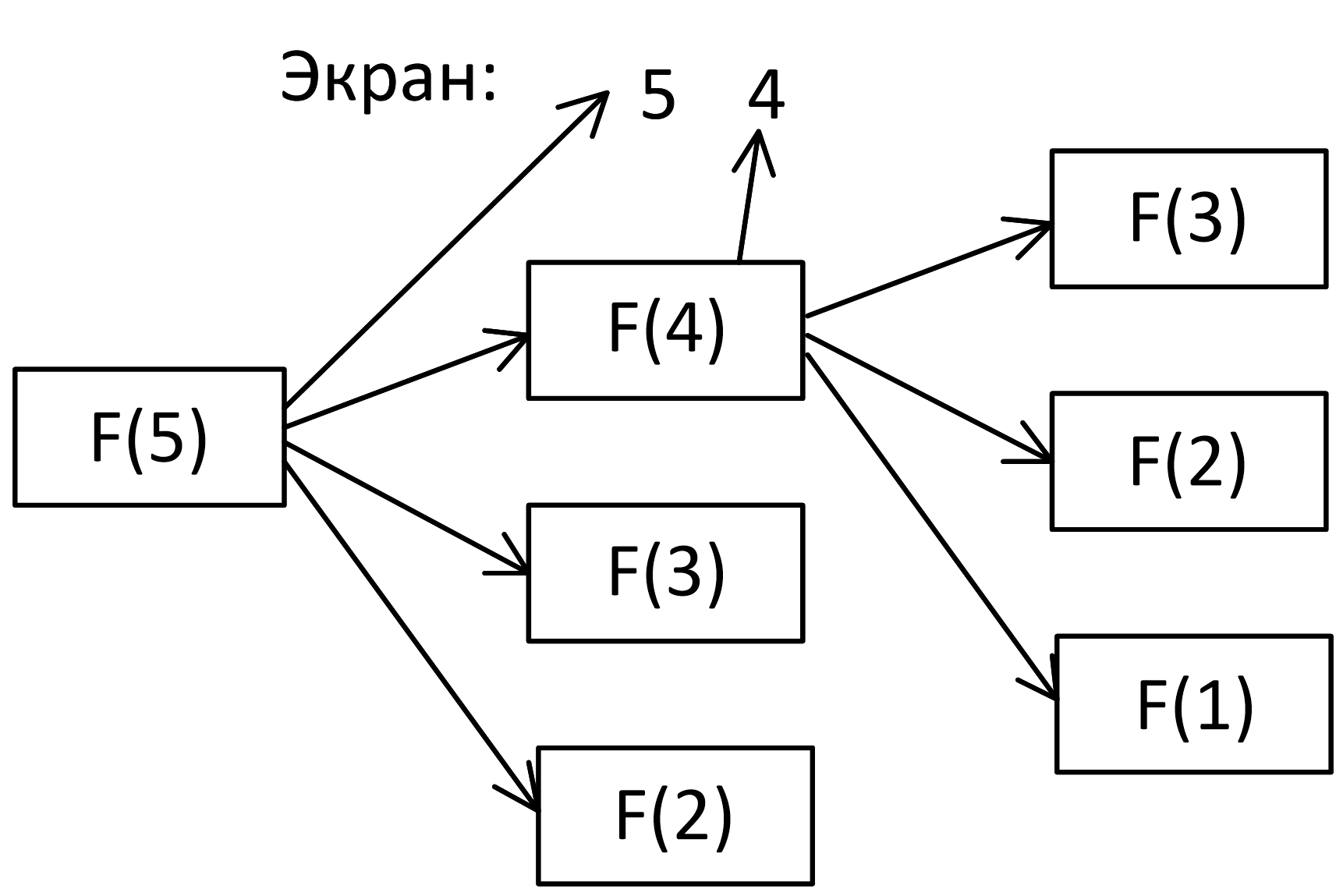
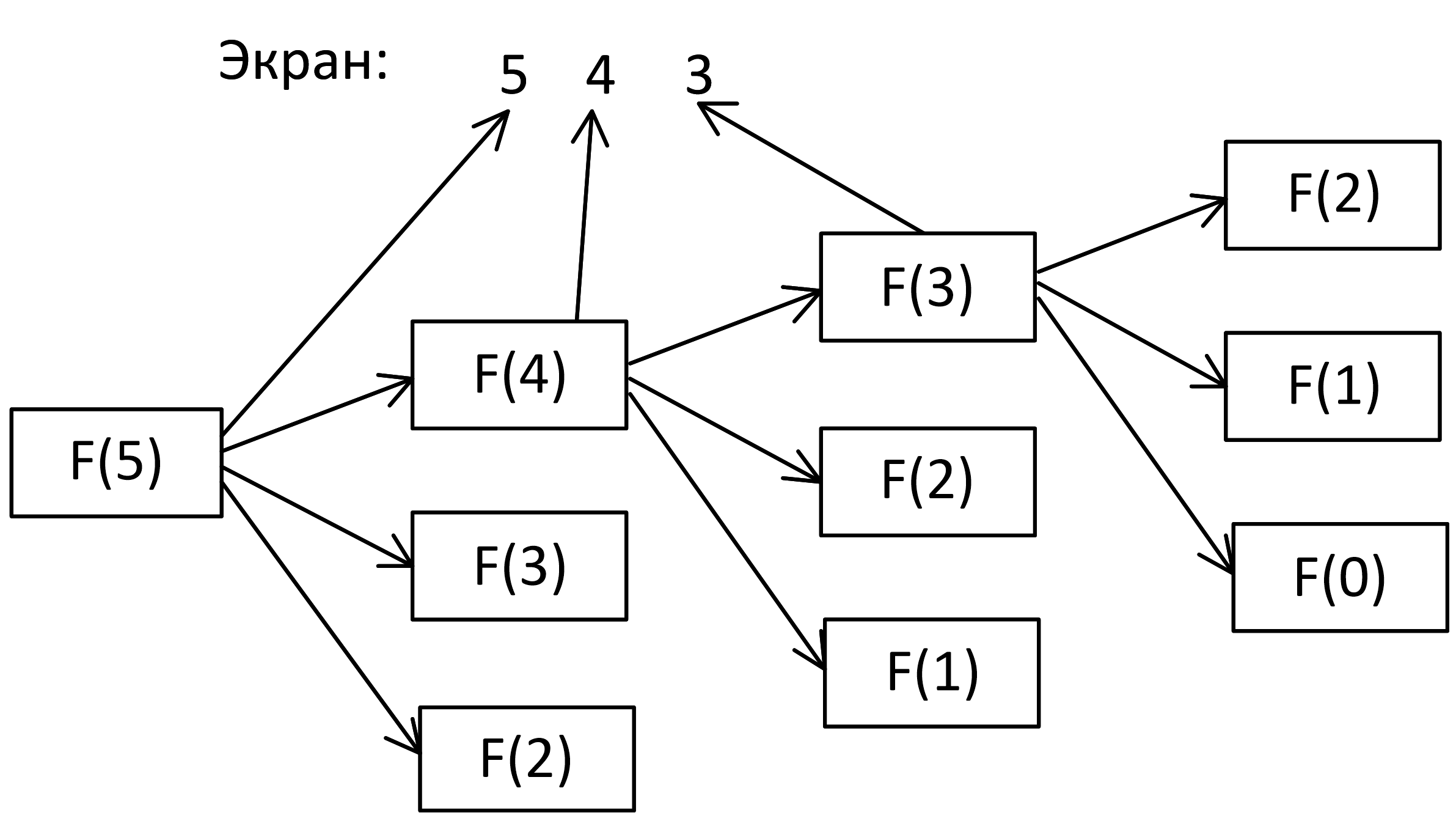
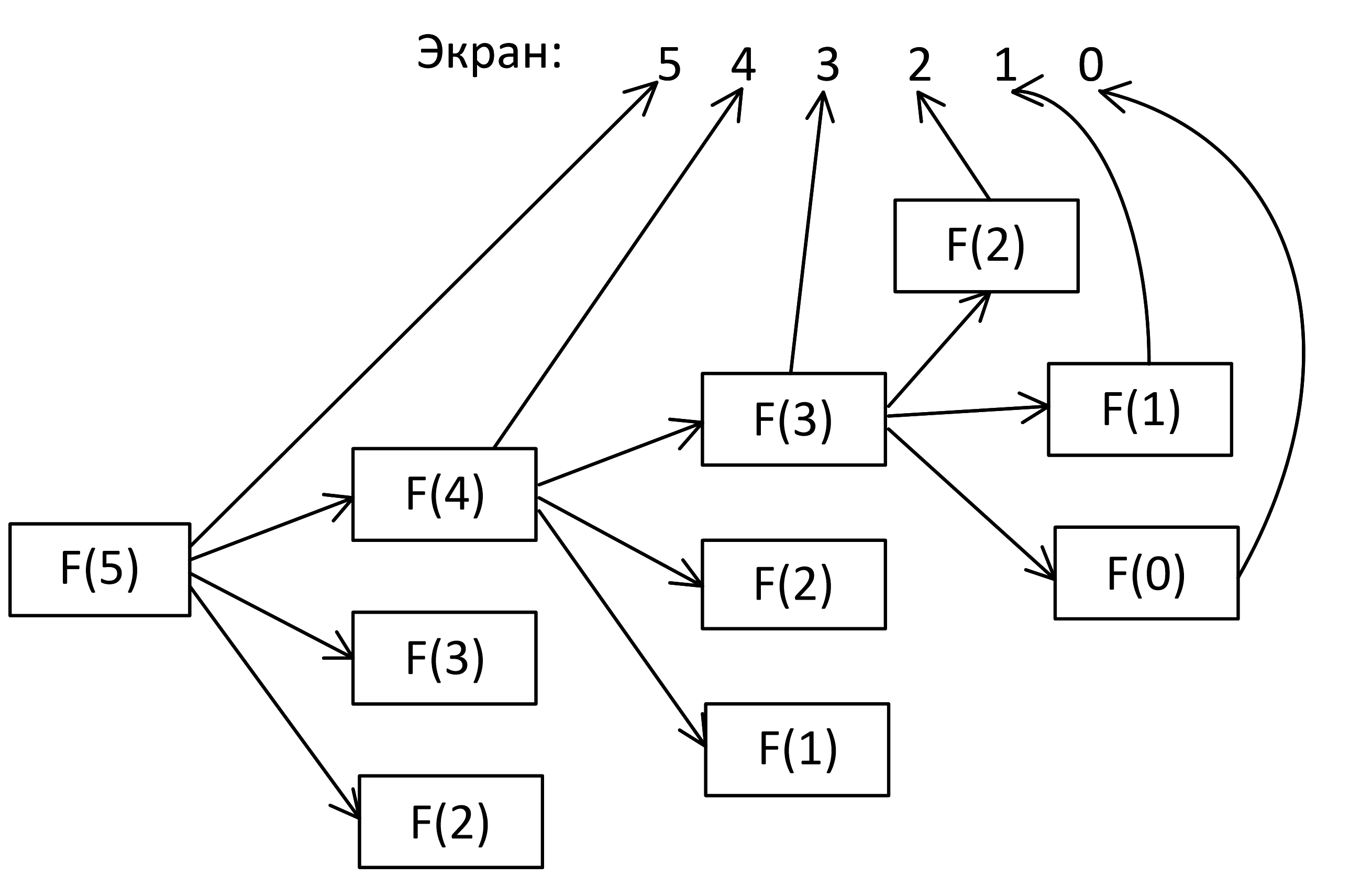
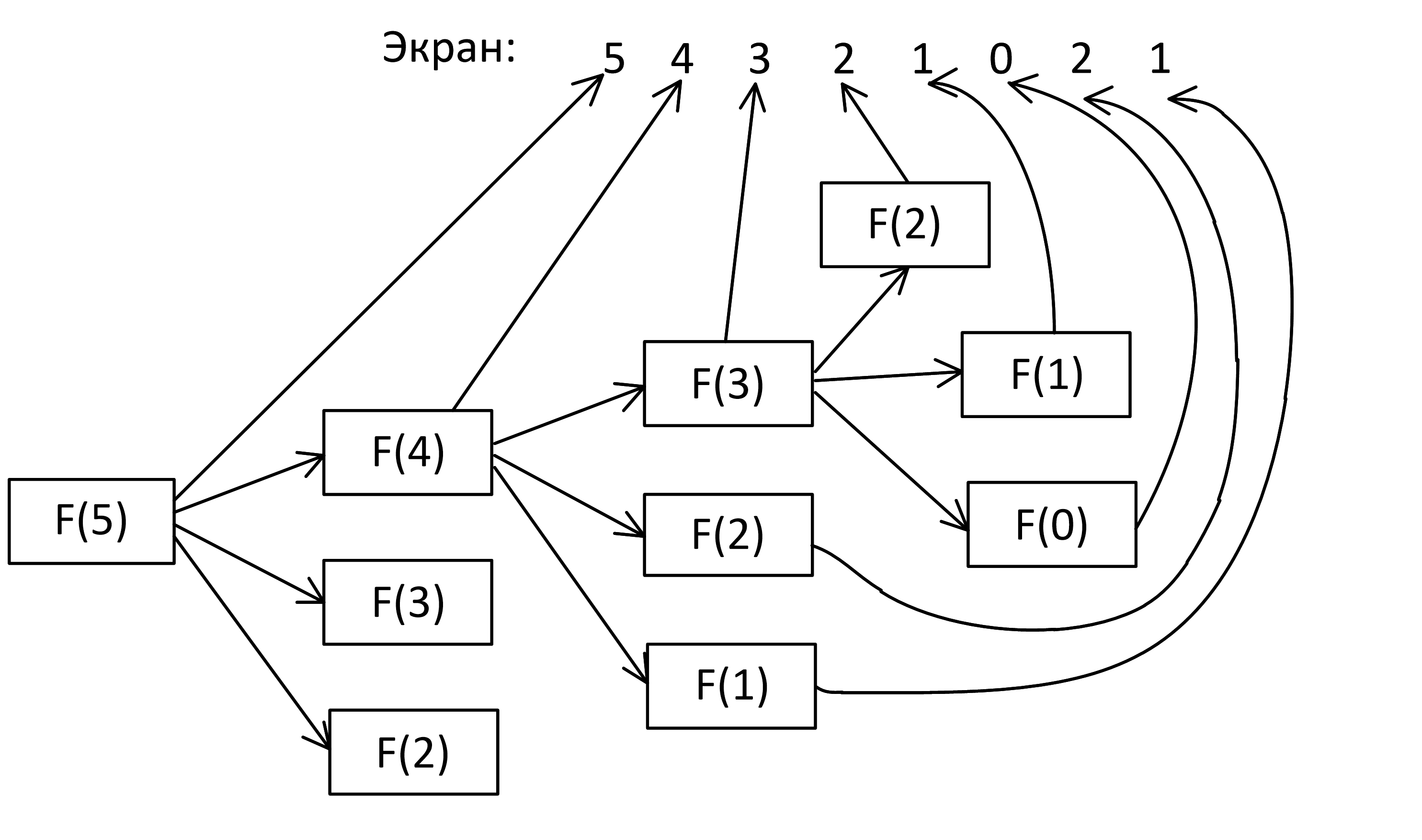
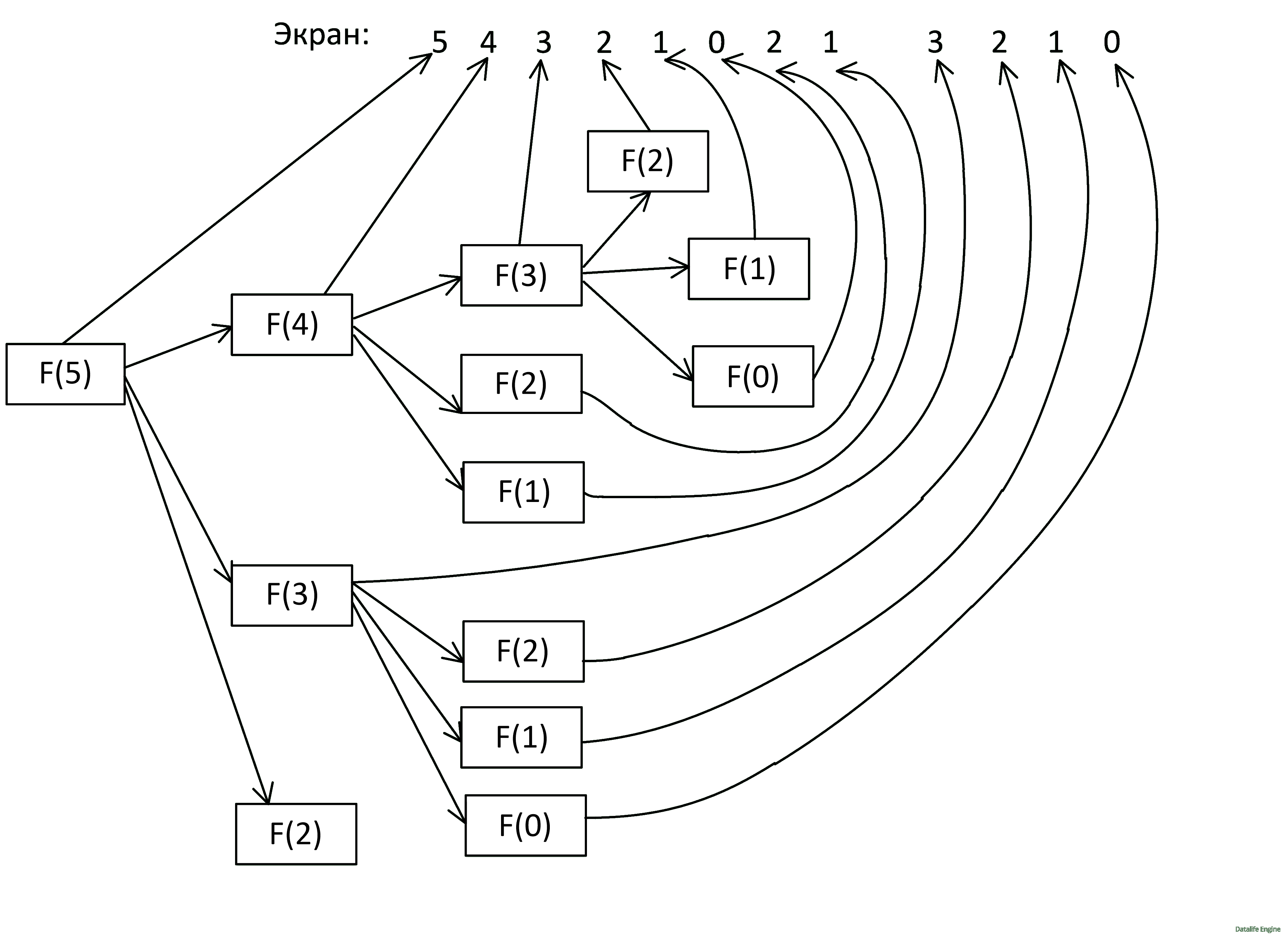
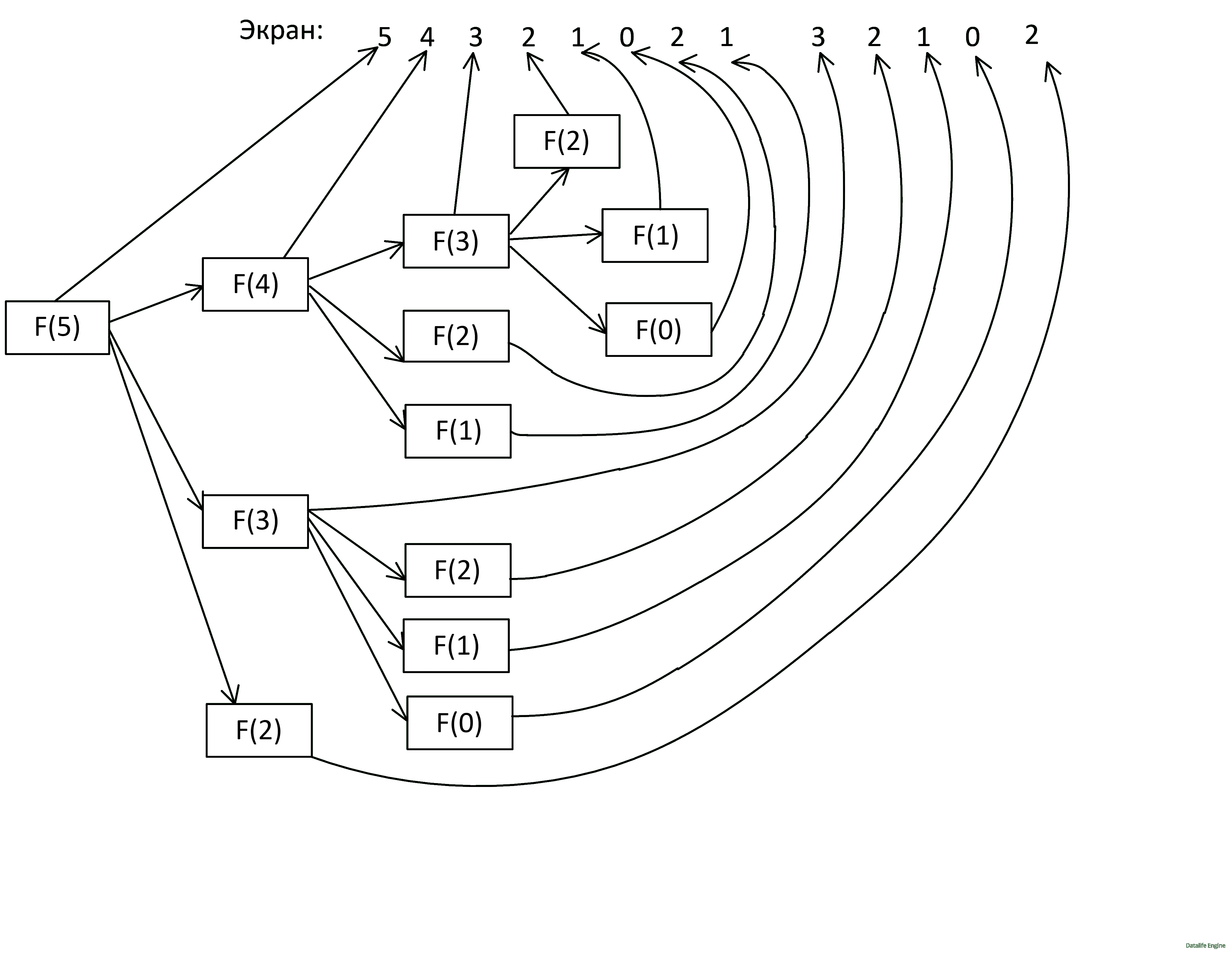
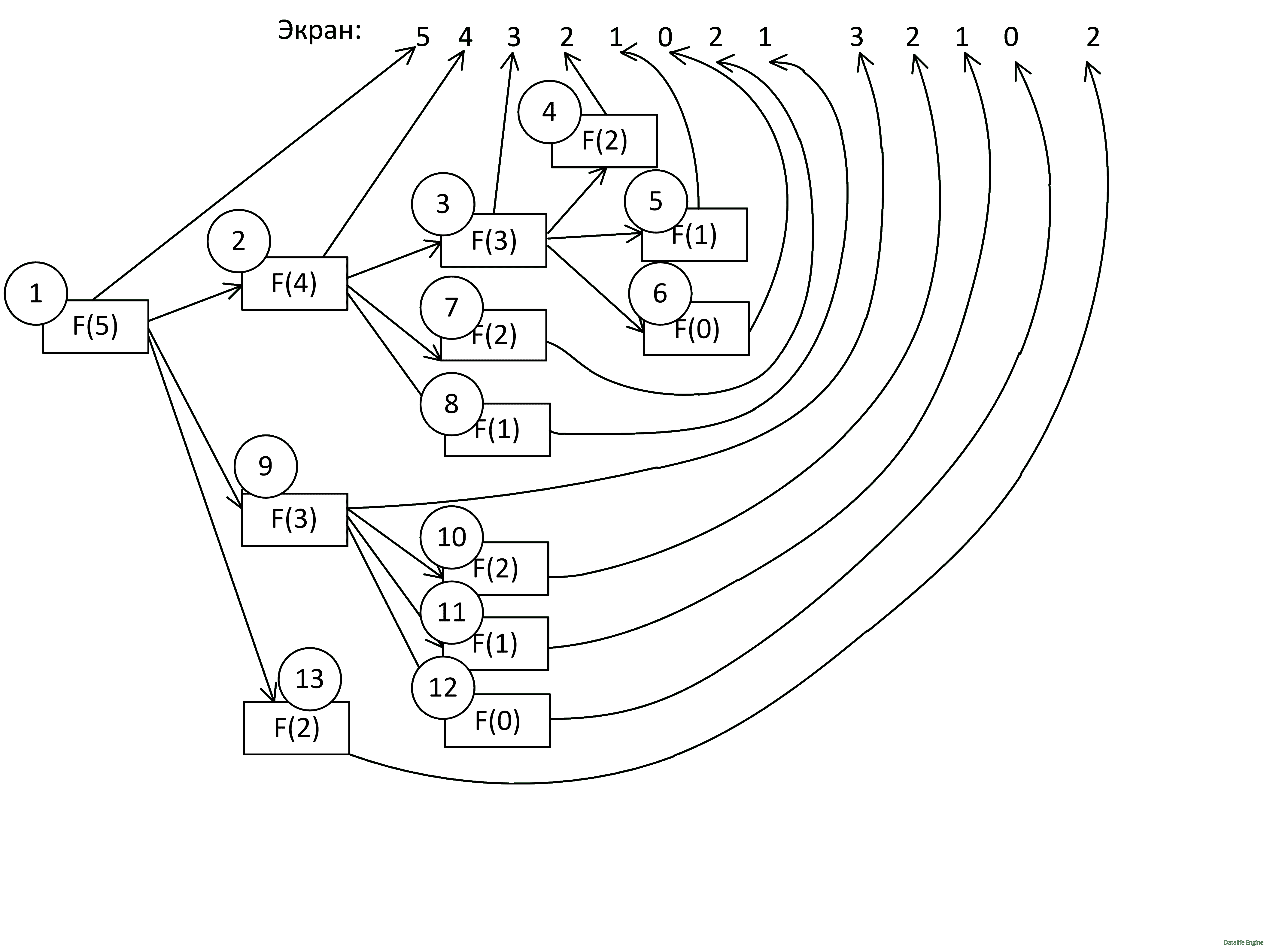
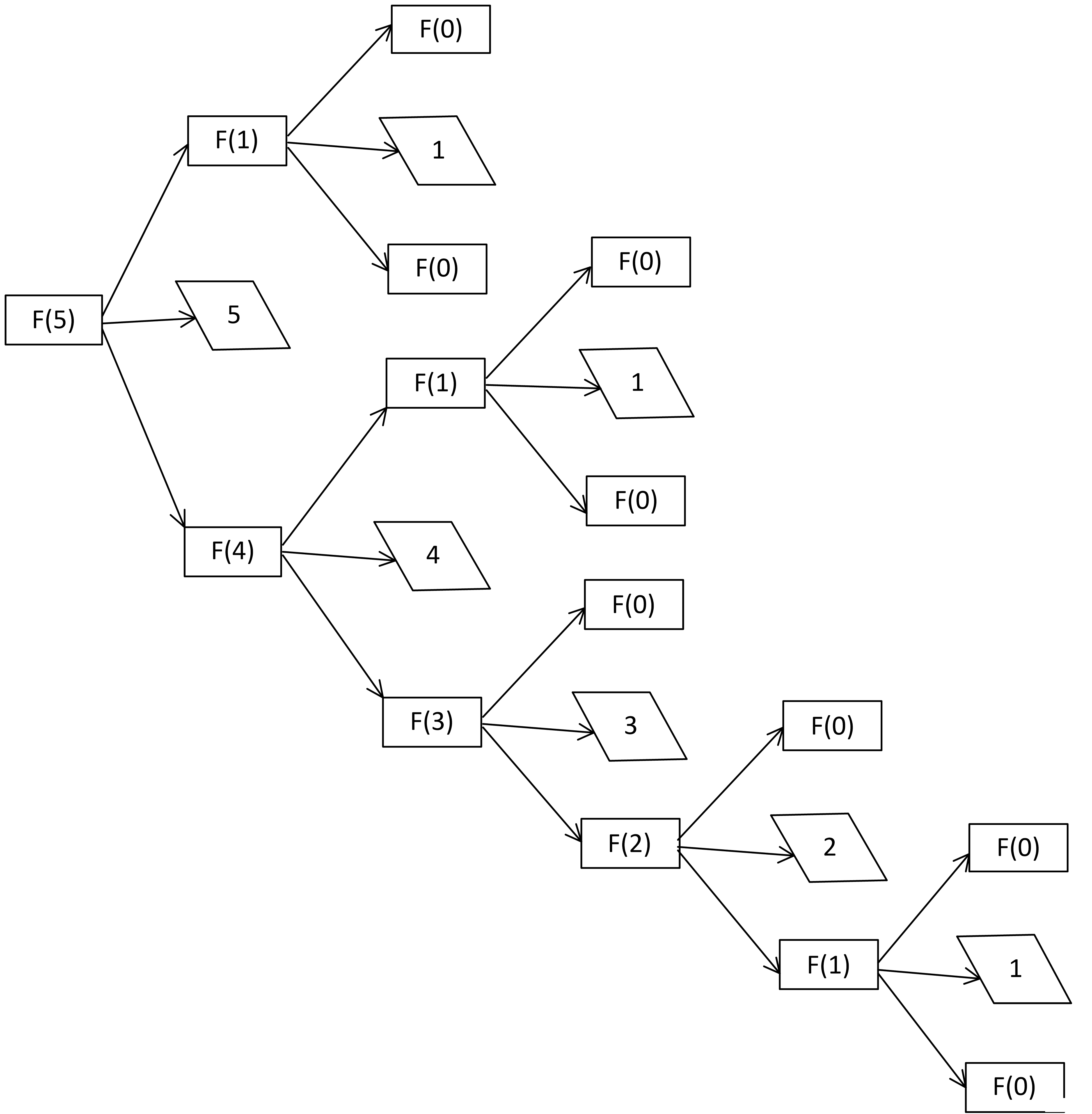
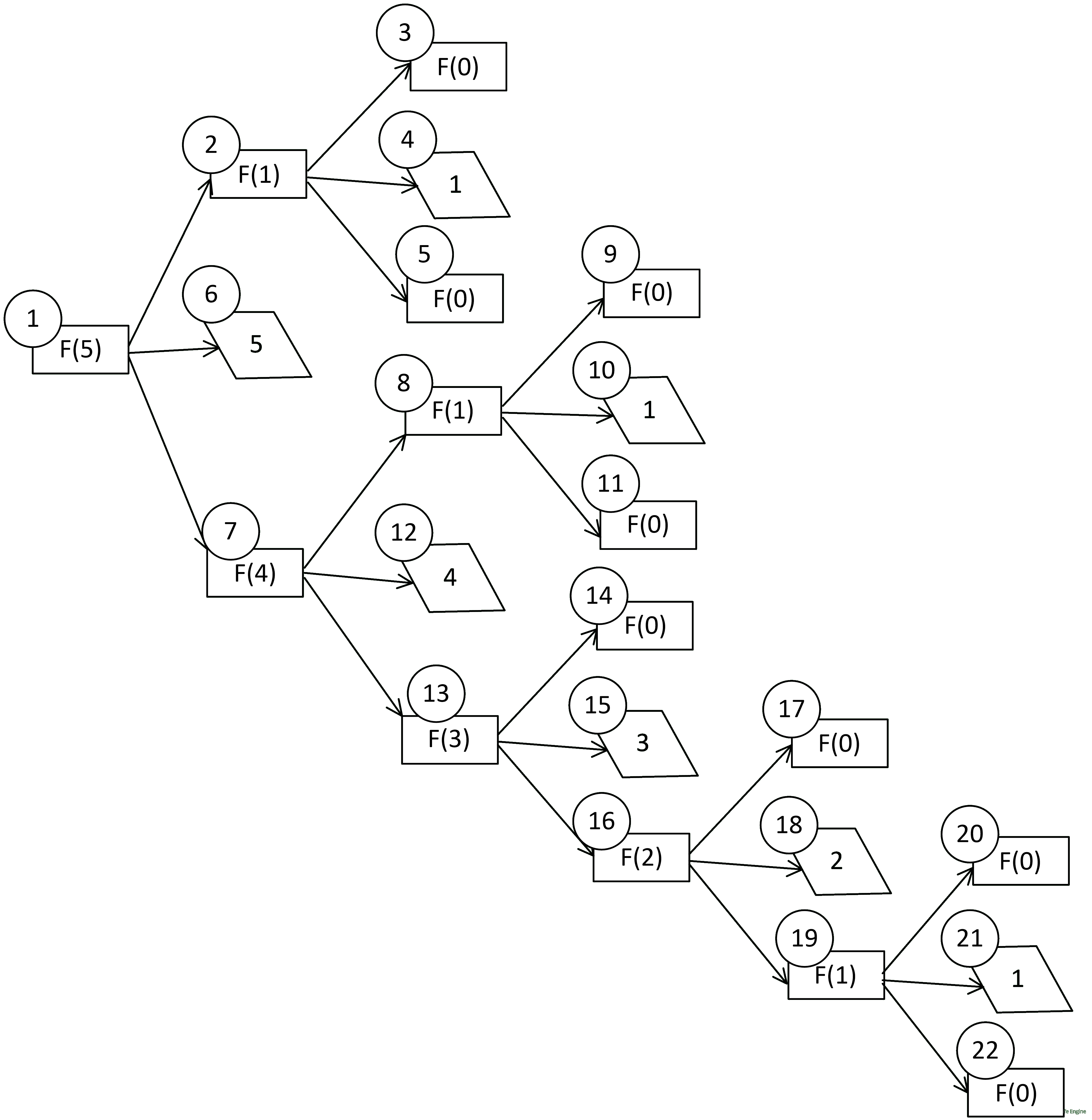
Задача 8.2.7. Ниже на пяти языках программирования записана рекурсивная функция (процедура) F.
|
Бейсик |
Python |
|
SUB F(n) PRINT n, IF n > 2 THEN F(n − 1) F(n − 2) F(n − 3) END IF END SUB |
def F(n): print (n, end='') if n > 2: F(n − 1) F(n − 2) F(n − 3) |
|
Паскаль |
Алгоритмический язык |
|
procedure F(n: integer); begin write(n); if n > 2 then begin F(n − 1); F(n − 2); F(n − 3) end end; |
алг F(цел n) нач вывод n если n > 2 то F(n − 1) F(n − 2) F(n − 3) все кон |
|
Си |
|
|
void F(int n ){ cout « n « endl; if (n > 2) { F(n - 1); F(n - 2); F(n - 3); } } |
|
Что выведет программа при вызове F(5)? В ответе запишите последовательность выведенных цифр слитно (без пробелов).
Задача 8.2.8. Ниже на пяти языках программирования записан рекурсивный алгоритм F.
|
Бейсик |
Python |
|
DECLARE SUB F(n) SUB F (n) IF n > 0 THEN F(n \ 4) PRINT n F(n - 1) END IF END SUB |
def F(n): if n > 0: F(n // 4) print(n) F (n - 1) |
|
Паскаль |
Алгоритмический язык |
|
procedure F(n: integer); begin if n > 0 then begin F(n div 4); write(n); F(n - 1); end end; |
алг F(цел n) нач если n > 0 то F(div(n, 4)) вывод n F(n - 1) все кон |
|
Си++ |
|
|
void F(int n){ if (n > 0){ F(n / 4) std::cout << n; F(n - 1); } } |
|
В качестве ответа укажите последовательность цифр, которая будет напечатана на экране в результате вызова F(5).