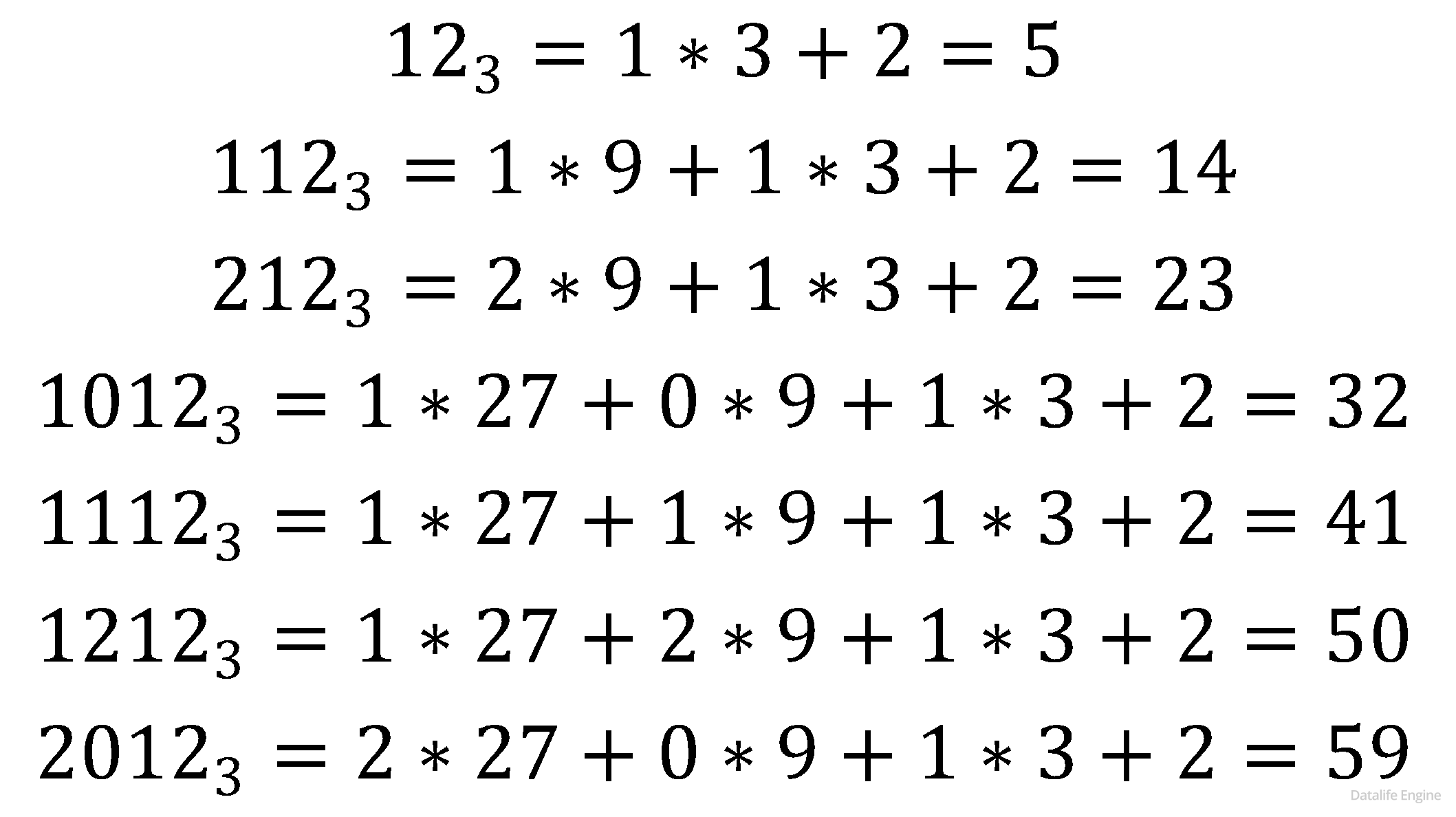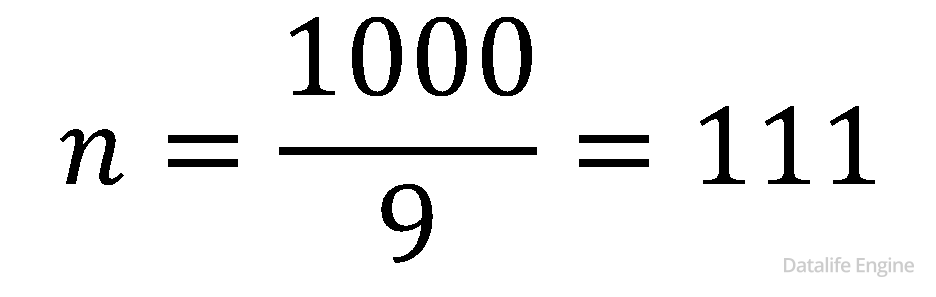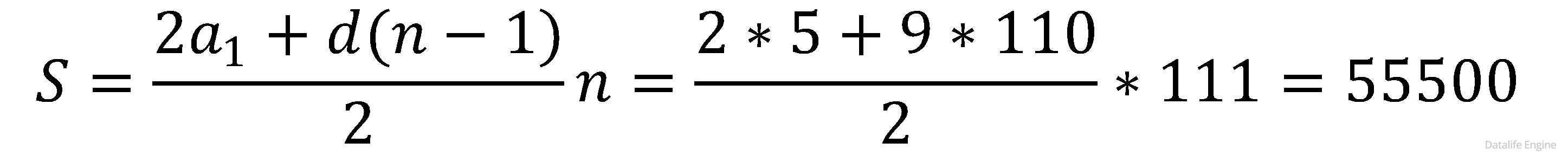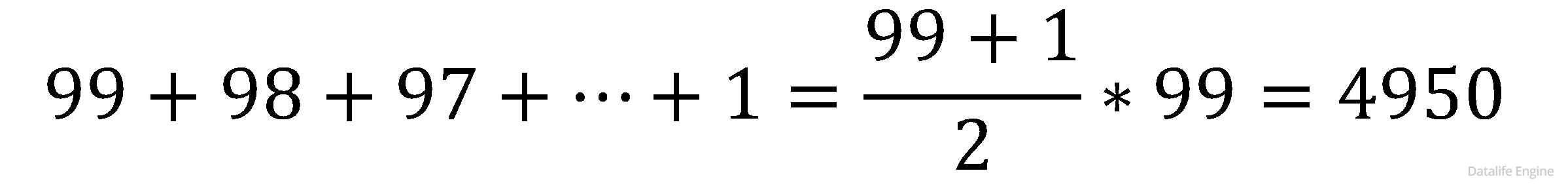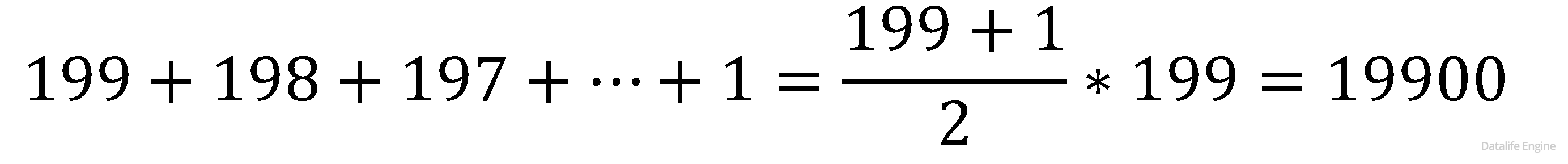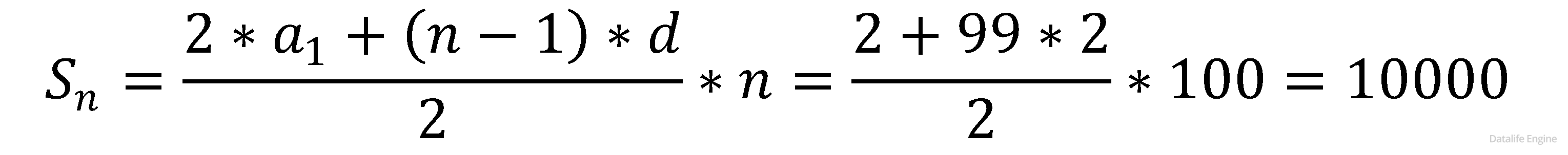Образовательный портал Павла Добряка

Задача на выявление цикла.

Выпишем степени двойки:

2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32, 2⁶ = 64, 2⁷ = 128, 2⁸ = 256, 2⁹ = 512, 2¹⁰ = 1024

Вглядимся на уже привычный нам ряд: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024…

Обратим внимание на последние цифры. Обнаружим, что по циклу повторяются (2, 4, 8, 6).

Выпишем показатели степени в таблицу

Последняя цифра степени	2	4	8	6
Показатели степени	1	2	3	4
	5	6	7	8
	9	10	11	12
	13	14	15	16
	…

 

Видно, что если остаток от деления показателя степени на 4 равен 1, то значение  степени оканчивается на 2; если остаток 2, то 4; если 3, то 8; если 0, то 6, например:

Степень	213	214	215	216
Значение степени	8 192	16 384	32 768	65 536
Последняя цифра степени	2	4	8	6
Вычисление остатка от деления показателя на 4	13 = 4*3 + 1	14 = 4*3 + 2	15 = 4*3 + 3	16 = 4*4 + 0

 

111 = 27 * 4 + 3

Следовательно,

2¹¹¹ = …8

Ответ: 8

Задача на цикл и прогрессию.

Посчитаем, сколько в каждой строке находится цифр. Поскольку с переходом к каждой новой строке предыдущая строка записывается два раза и добавляется новая цифра, то

S(0) = 1

S(n) = S(n – 1) * 2 + 1

n	S(n)
1	1
2	3
3	7
4	15
5	31
6	63
7	127
8	255
9	511
10	1023

 

Мы ищем в 10 строке символ под номером 504. Он находится в левой половине строчки, следовательно, совпадает с символом под номером 504 в 9 строке. Рассмотрим концовку строки №9:

Номер символа в строке	…	504	505	506	507	508	509	510	511
Конец строки №9	…	1	2	3	4	5	6	7	8

 

Ответ: 1

Эта задача является модификацией задачи 1.3.6.

Сконструируем такие числа:

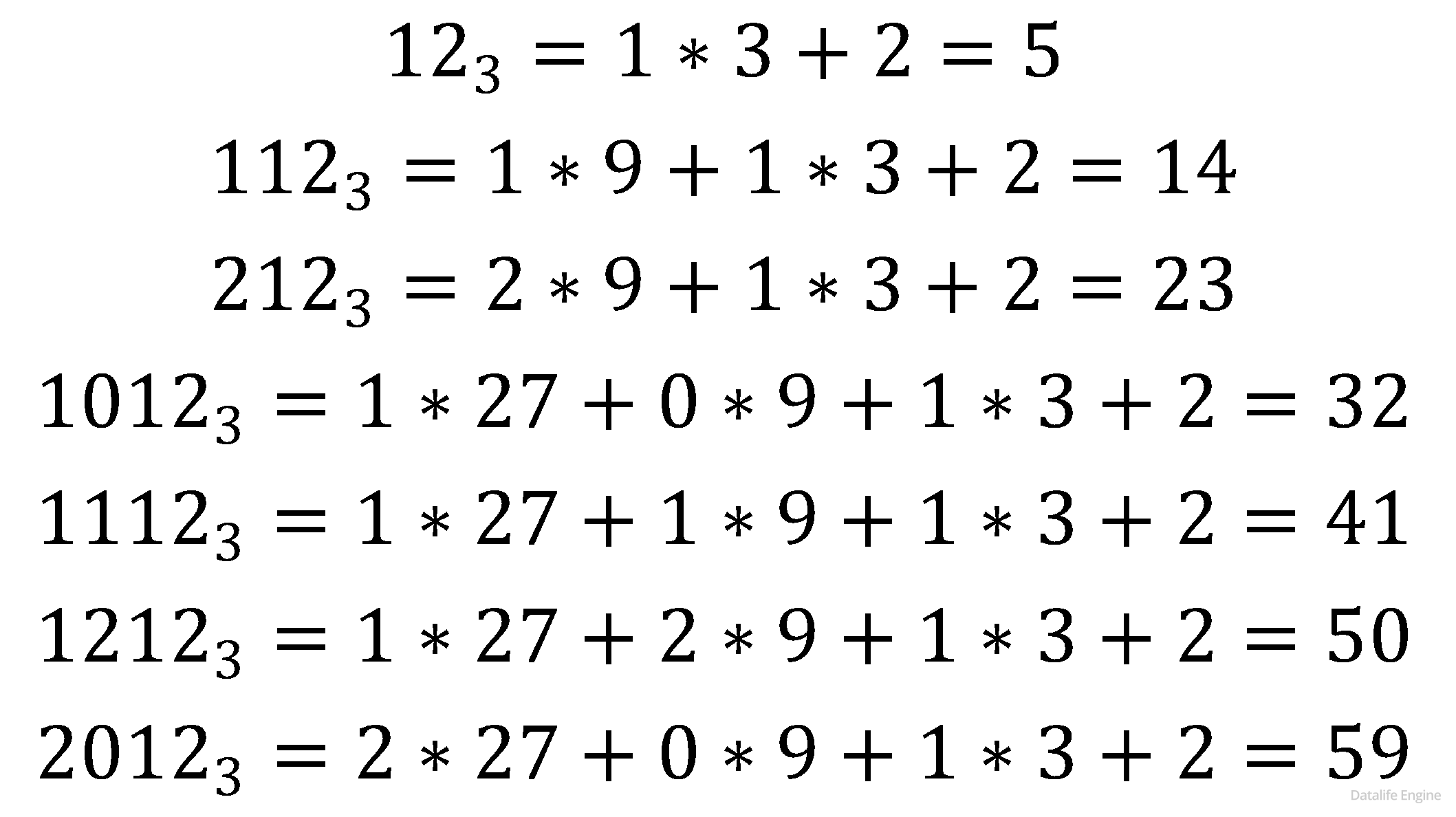
Видно, что каждое следующее число больше предыдущего на 9, то есть они образуют арифметическую прогрессию с разностью d = 9, a₁ = 5.  

Всего таких чисел:

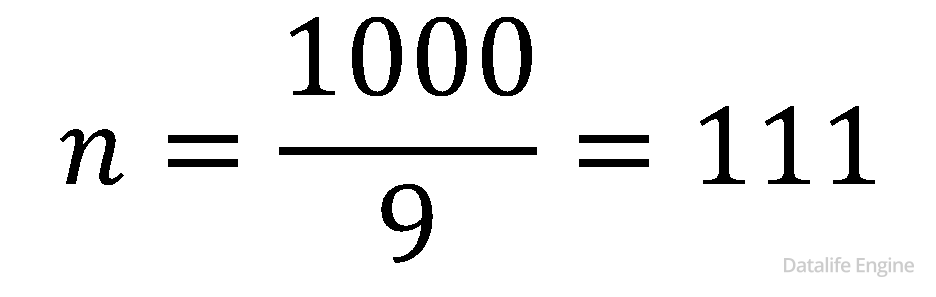
По формуле суммы членов арифметической прогрессии:

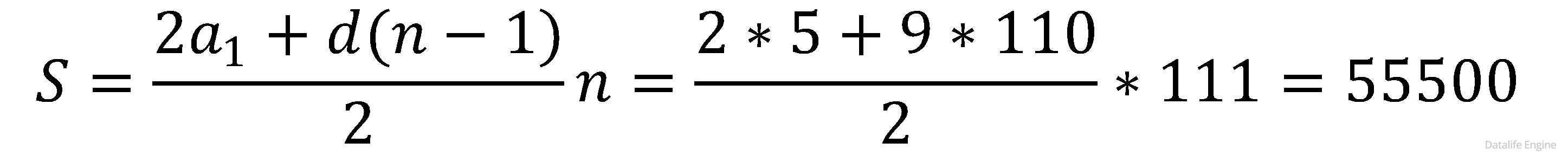
Ответ: 55500

Задача на арифметическую прогрессию. Задача похожа на задачу 2.2.4.

Зафиксируем одну букву А на первом месте. Тогда возможно 99 расположений второй буквы А:

Место	1	2	3	4	5	…	98	99	100
Слово	A
		Одна буква А и 99 букв B

 

Переместим первую букву А на второе место, тогда для второй буквы А останется 98 мест (на первое место мы её поставить не можем, так как случай AAB…B уже учтен в предыдущей таблице):

Место	1	2	3	4	5	…	98	99	100
Слово	B	А
			Одна буква А и 98 букв B

 

Переместим первую букву А на третье место, тогда для второй буквы А останется 97 мест:

Место	1	2	3	4	5	…	98	99	100
Слово	B	B	А
				Одна буква А и 97 букв B

 

Двигая первую букву дальше, мы дойдем до предела, получив всего одно слово:

Место	1	2	3	4	5	…	98	99	100
Слово	B	B	B	B	B		B	A	A

 

Сложим результаты и посчитаем по формуле суммы членов арифметической прогрессии:

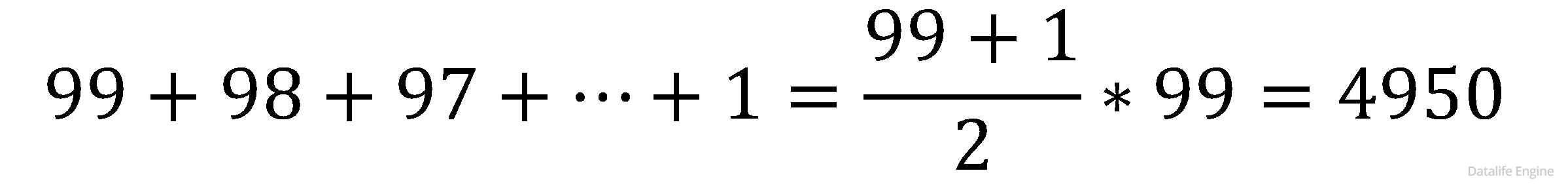
Ответ: 4950.

Задача на выявление цикла. Задача аналогична задаче 7.2.2.

Мысленно расставим на плоскости по кругу 200 вершин (ребра проводить не будем).

Соединим первую вершину со всеми остальными и получим 199 ребер.

Соединим вторую вершину со всеми остальными, кроме первой (с первой она уже соединена), и получим еще 198 ребер.

Третью вершину соединим с остальными, кроме первой и второй, и получим 197 ребер.

И т.д.

Предпоследнюю вершину соединим с последней 1 ребром:

Сложим результаты и посчитаем по формуле суммы членов арифметической прогрессии:

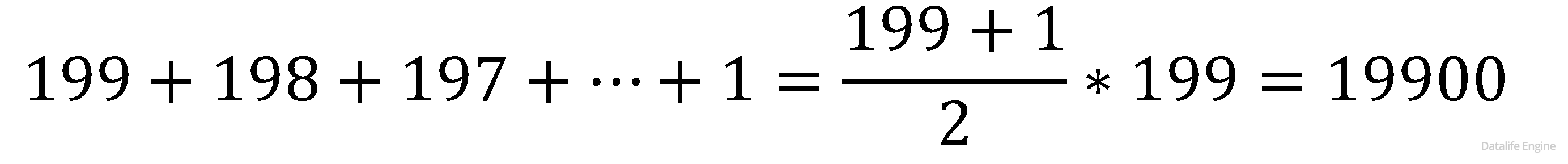
Ответ: 19900

Начнем формировать фрагменты и посчитаем количество зеленых бусин:

Номер фрагмента	Фрагмент	Количество зеленых бусин
1	ЗЗЗ	3
2	ЖЗЗЗГ	3
3	ОЗЗЗЗЗС	5
4	KЗЗЗЗЗЗЗФ	7
5	ФЗЗЗЗЗЗЗЗЗК	9
6	СЗЗЗЗЗЗЗЗЗЗЗО	11
7	ГЗЗЗЗЗЗЗЗЗЗЗЗЗЖ	13
8	ЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗ	17
9	ЖЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗГ	17
10	ОЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗС	19

 

Видно, что поскольку у нас 7 цветов, то каждый седьмой фрагмент будет содержать только бусины зеленого цвета, то есть полностью зелеными будут 1, 8, 15, 22, … фрагменты.

Если начать подсчитывать количество зеленых бусин, то оно каждый раз увеличивается на 2 (то есть составляет арифметическую прогрессию) с добавочными двумя зелеными бусинами в каждом из 7 фрагментов:

Номер фрагмента	Фрагмент	Количество зеленых бусин по прогрессии	Добавочные бусины
1	ЗЗЗ	1	2
2	ЖЗЗЗГ	3
3	ОЗЗЗЗЗС	5
4	KЗЗЗЗЗЗЗФ	7
5	ФЗЗЗЗЗЗЗЗЗК	9
6	СЗЗЗЗЗЗЗЗЗЗЗО	11
7	ГЗЗЗЗЗЗЗЗЗЗЗЗЗЖ	13
8	ЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗ	15	2
9	ЖЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗГ	17
10	ОЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗЗС	19

 

Количество зеленых бусин в 100 фрагментах считаем по формуле суммы членов  арифметической прогрессии:

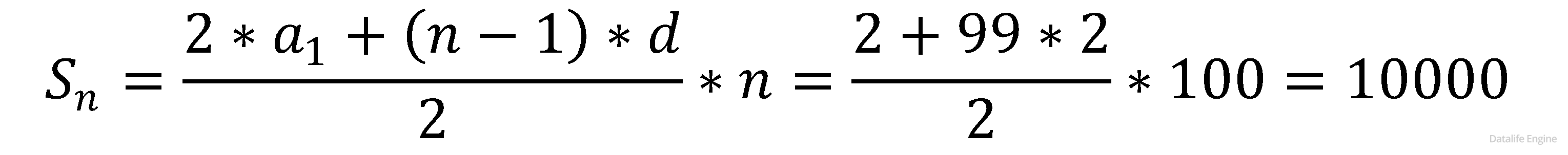
Из первых ста количество фрагментов, в которых все бусы зеленые, равно целому от деления 100/7 = 14.

Таким образом, количество зеленых бусин в первых 100 фрагментах равно 10000 + 14 * 2 = 10028.

Ответ: 10028.

Задача на последовательность чисел Фибоначчи. Решайте аналогично задаче 3.2.9.

Выпишем возможные результаты от 1 до 11 и посчитаем количество программ.

Из 1 в 1 ведет одна пустая программа:

Результат программы	Количество программ
1	1

 

Из 1 в 2 мы можем попасть одним путем: 1 + 1 = 2

Результат программы	Количество программ
1	1
2	1

 

В 3 мы можем попасть двумя путями: 1 + 2 = 3 и 2 + 1 = 3:

Результат программы	Количество программ
1	1
2	1
3	2

 

В 4 мы можем попасть из чисел 2 и 3 следующими путями: 2 + 2 = 4 и 3 + 1 = 3, но так как в 3 из 1 мы можем попасть двумя путями, то у нас имеются три пути из 1 в 4:

1 + 1 + 2 = 4,

1 + 1 + 1 + 1 = 4,

1 + 2 + 1 = 4.

То есть кол-во путей С(4) = С(3) + С(2):

Результат программы	Количество программ
1	1
2	1
3	2
4	3

 

Аналогично для 5: С (5) = С(4) + С(3).

Фактически количество программ равняется сумме двух предыдущих значений:

С(n) = C(n – 1) + C(n – 2).

Мы имеем дело с последовательностью чисел Фибоначчи:

Результат программы	Количество программ
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89

 

Ответ: 89

Задача на степень двойки. Составьте таблицу, как в предыдущей задаче.

Рекурсивно посчитаем количество программ. Значение в каждой следующей строчке равно сумме всех предыдущих:

Результат программы	Количество программ
1	1
2	1
3	2
4	4
5	8
6	16
7	32
8	64

 

Видно, что количество программ равно степени двойки с показателем, равным номеру строки минус 2:

C(n) = 2^{n – 2}

Посчитаем количество программ при n=12:

C(12) = 2¹⁰ = 1024

Ответ: 1024

Задача является модификацией задачи 6.5.2. Выявите цикл.

Дано 1000«1» + 1000«2».

Выполняем заменить (111, 2):

1000«1» + 1000«2» → 1«2» + 997«1» + 1000«2».

Далее выполняется второе действие цикла - заменить (222, 1):

1«2» + 997«1» + 1000«2» → 1«2» + 997«1» + 1«1» + 997«2» = 1«2» + 998«1» + 997«2».

Итак, за первый проход цикла:

1000«1» + 1000«2» → 1«2» + 998«1» + 997«2».

Аналогично выполняем второй проход цикла:

1«2» + 998«1» + 997«2» → 2«2» + 996«1» + 994«2».

Выполнение третьего прохода цикла отличается от двух предыдущих:

2«2» + 996«1» + 994«2» → 3«2» + 993«1» + 994«2» → 994«1» + 994«2». 

Получается, что за три прохода цикла у нас исчезли шесть единиц и шесть двоек:

1000«1» + 1000«2» → 994«1» + 994«2».

Следующие три прохода цикла окажут такое же действие:

994«1» + 994«2» → 988«1» + 988«2». 

Получается, что исходная последовательность всё время «тает» на шесть единиц и двоек:

1000«1» + 1000«2» → (1000 – 6 – 6 – … – 6)«1» + (1000 – 6 – 6 – … – 6)«2».

1000 = 166 * 6 + 4.

Вычтем из исходной последовательности 165 шестерок единиц и двоек (оставим некоторый запас, чтобы убедиться, что в конце алгоритм работает так же, как и в начале):

1000«1» + 1000«2» → 10«1» + 10«2» → 1«2» + 7«1» + 1«1» + 7«2» = 1«2» + 8«1» + 7«2» → 2«2» + 5«1» + 1«1» + 4«2» = 2«2» + 6«1» + 4«2» → 3«2» + 3«1» + 4«2» → 1«1» + 3«1» + 4«2» = 4«1» + 4«2» → 1«2» + 1«1» + 1«1» +  1«2» = 1«2» + 2«1» +  1«2».

Ответ: 2112

Задача аналогична 2.5.1. Придумайте способ, как ускорить вычисления. Задача на степень двойки.

Если сигнал длины 1, то мы можем закодировать 2¹ = 2 символа.

Если сигнал длины 2, то мы можем закодировать 2² = 4 символа.

Если сигнал длины 3, то мы можем закодировать 2³ = 8 символов.

И т. д.

Результаты просуммируем:

2¹ + 2² + 2³ + 2⁴ + … + 2¹⁰ = 2 + 4 + 8 + 16 + … + 1024

Начнем записывать степени двойки в таблицу, одновременно считая накапливающуюся сумму:

Показатель степени	Значение степени двойки	Накапливающаяся сумма
1	2	2
2	4	6
3	8	14
4	16	30
5	32	62
6	64	126

 

Заметим, что накапливающаяся сумма на 2 меньше, чем следующая степень:

S_n = 2ⁿ⁺¹ – 2

Следовательно 

S₁₀ = 2¹¹ – 2 = 2048 – 2 = 2046

Ответ: 2046