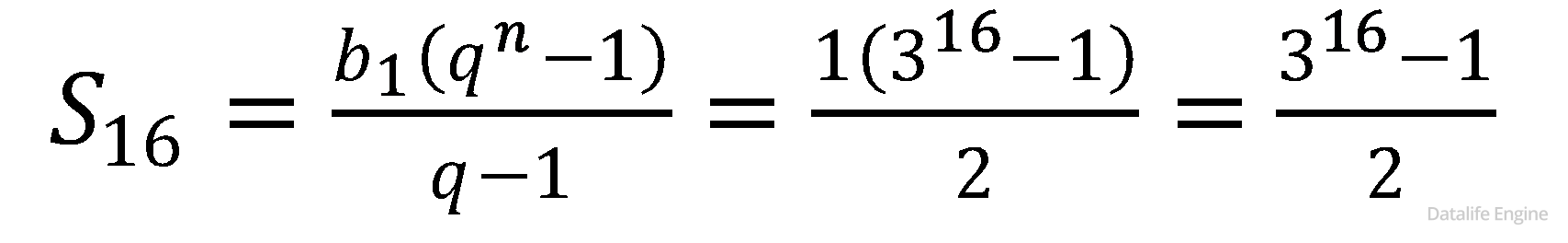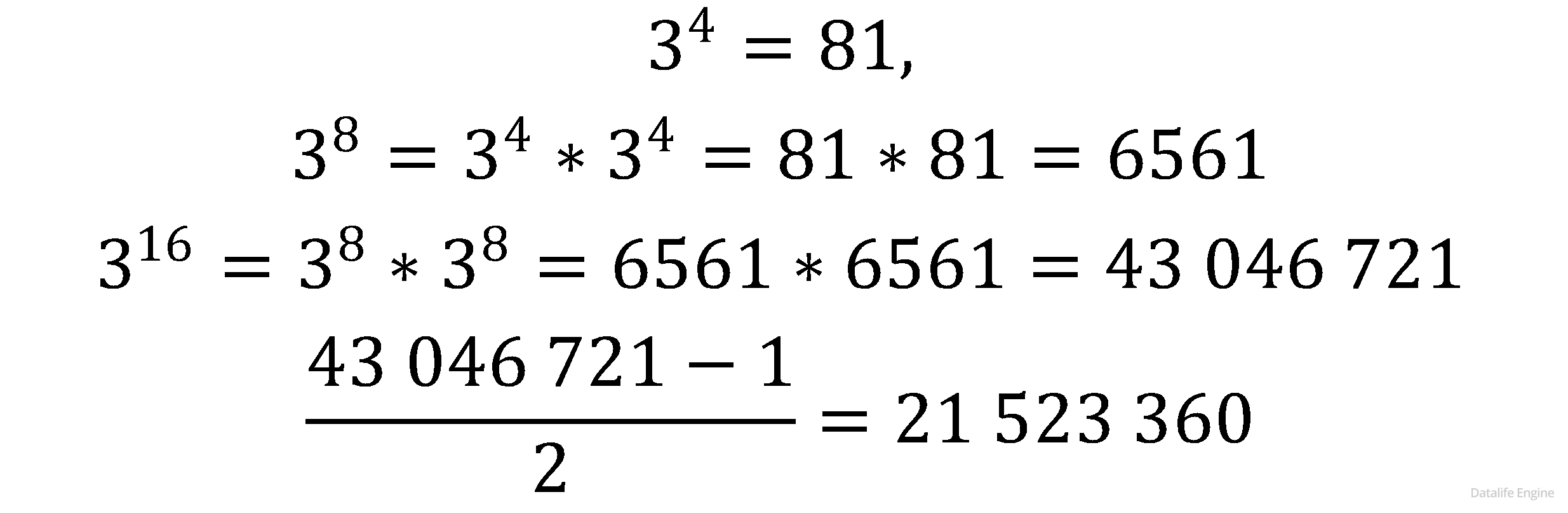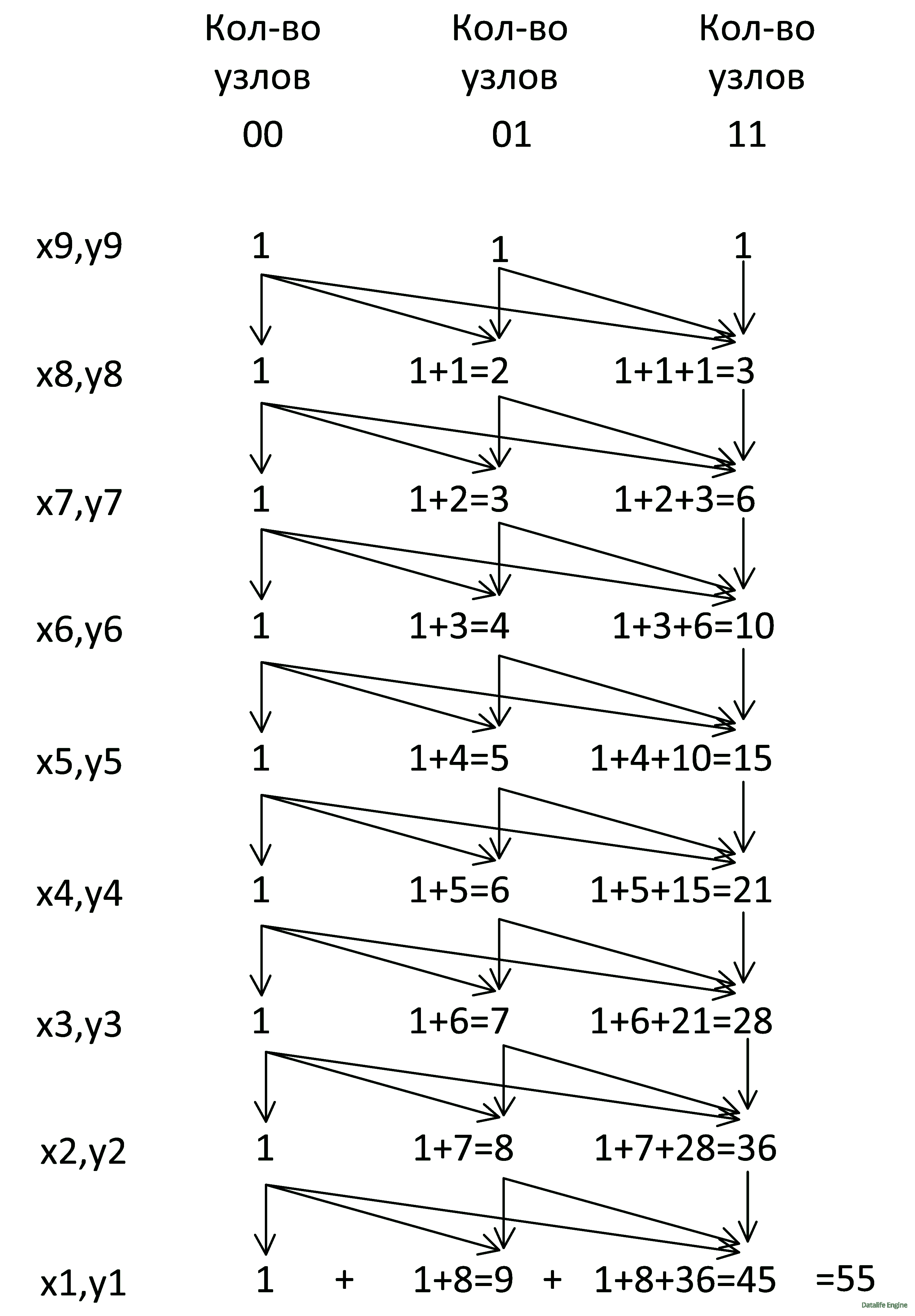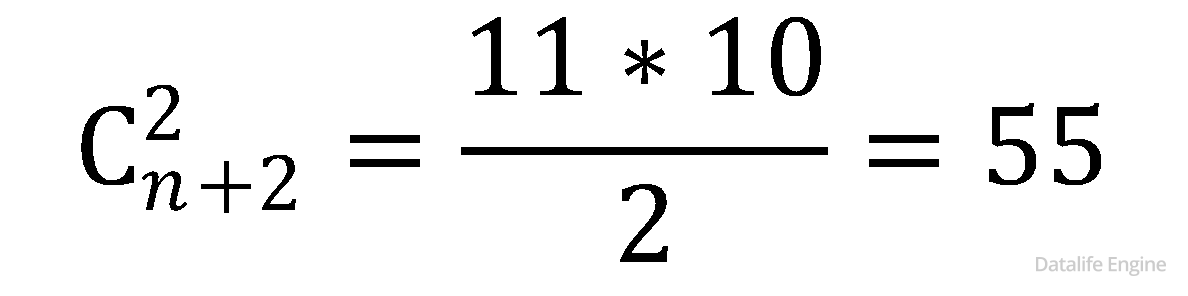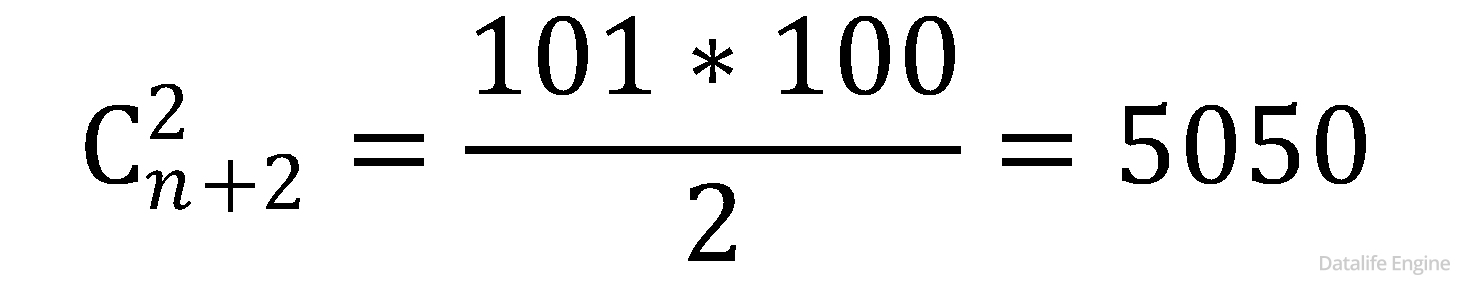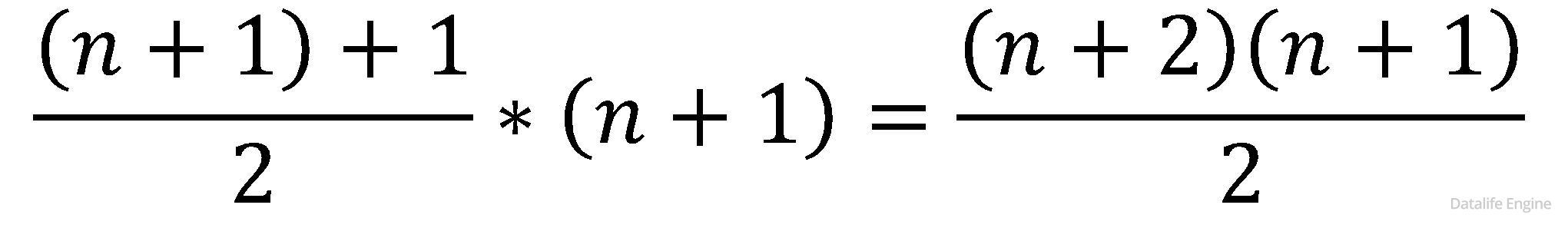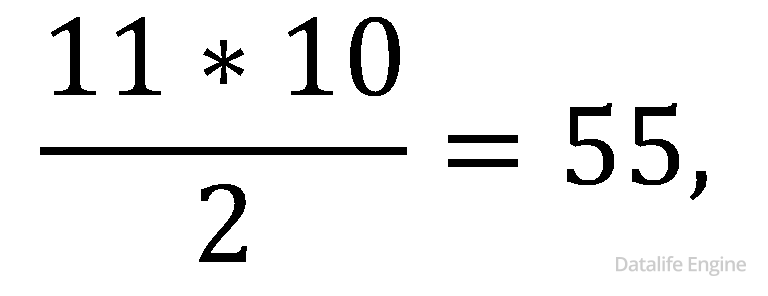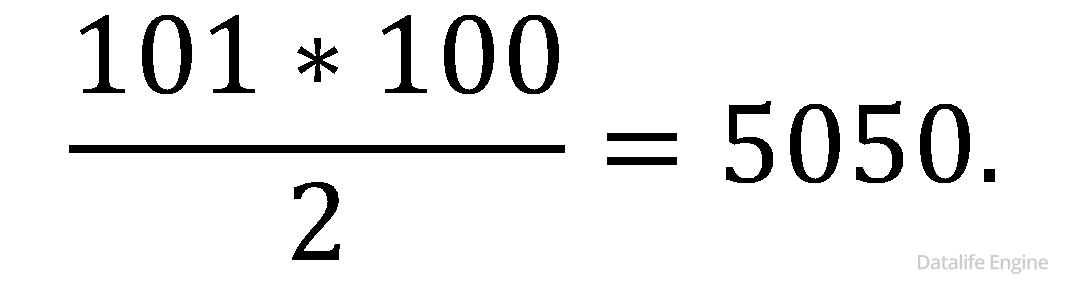Образовательный портал Павла Добряка

Начнем строить дерево.

x1 и x2, очевидно, может принимать любые значения:

Рассмотрим ветку x1 = 0, x2 = 0:

(x1 → x2) → (x2 → x3) = (0 → 0) → (0 → x3) = 1 → (0 → x3) = 0 → x3 = 1

x3 – любое:

Рассмотрим ветку x1 = 0, x2 = 1:

(x1 → x2) → (x2 → x3) = (0 → 1) → (1 → x3) = 1 → (1 → x3) = 1 → x3 = x3

x3 = 1:

Рассмотрим ветку x1 = 1, x2 = 0:

(x1 → x2) → (x2 → x3) = (1 → 0) → (0 → x3) = 0 → (0 → x3) = 1

x3 – любое:

Рассмотрим ветку x1=1, x2=1:

(x1 → x2) → (x2 → x3) = (1 → 1) → (1 → x3) = 1 → (1 → x3) = 1 → x3 = x3

x3 = 1:

 Объединяя случаи, сформулируем правила построения дерева: 0 ветвится, после 1 всегда идет 1.

Пользуясь этими правилами, построим еще два уровня дерева:

Нам нужен сотый уровень. Посчитаем количество узлов на каждом уровне и увидим закономерность:

На каждом уровне количество узлов равно удвоенному номеру уровня.

Ответ: 200.

Введите новые обозначения, начните строить дерево и найдите закономерность. Задача на сумму членов геометрической прогрессии. Воспользуйтесь алгоритмом быстрого возведения в степень.

Введем новые обозначения и получим систему уравнений:

y1 → y2 = 1

y2 → y3 = 1

…

y14 → y15 = 1

Это хорошо знакомое нам дерево. Построим его фрагмент:

Возвращаясь к исходным обозначениям, определим, сколько решений по x есть в каждом узле:

При y1 = 0 x1 → x2 = 0 Одно решение: x1 = 1, x2 = 0.

При y1 = 1 x1 → x2 = 1 Три решения:  x1 = 0, x2 = 0; x1 = 0, x2 = 1; x1 = 1, x2 = 1.

Отметим количество решений на дереве:

Количество решений по каждой ветке перемножается, результаты нужно сложить:

Количество решений – это сумма членов геометрической прогрессии с b₁ = 1 и q = 3. На 15 уровне у нас 16 слагаемых. Посчитаем количество решений по формуле суммы членов геометрической прогрессии:   

Остается посчитать   быстрым способом: 

Ответ: 21 523 360

Задача похожа на задачу 4.5.8. Постройте фрагмент дерева, затем стройте рекурсивное дерево подсчета количества узлов.

Начнем строить дерево. Очевидно, что x1 и y1 могут быть любыми:

При x1 = 0, x2 = 0: x1 ∧ x2 ∨ x3 = 0 ∧ 0 ∨ x3 = x3 x3 = 1.	При x1 = 1, x2 = 0: x1 ∧ x2 ∨ x3 = 1 ∧ 0 ∨ x3 = 0 ∨ x3 = x3 x3 = 1.
При x1 = 0, x2 = 1: x1 ∧ x2 ∨ x3 = 0 ∧ 1 ∨ x3 = 0 ∨ x3 = x3 x3 = 1.	При x1 = 1, x2 = 1: x1 ∧ x2 ∨ x3 = 1 ∧ 1 ∨ x3 = 1 ∨ x3 = x3 x3 - любое.

Сформулируем правила построения дерева:

1. После 0 идет 1 (исключение – второй уровень)
2. После 1, которая идет после 0, идет 1
3. После двух 1 идет ветвление.

Построим несколько уровней дерева:

Дерево быстро ветвится. На его основе построим рекурсивное дерево подсчета количества узлов:

Ответ: 73

Начните строить тетрарное дерево (в обратном порядке), а когда увидите, что ветвей стало слишком много, постройте дерево обсчета количества узлов (как в задаче 4.5.8). Затем обнаружьте связь с комбинаторикой.

Решим задачу двумя способами. Первый способ - как в подсказке, второй способ – путем упрощения выражений с помощью новых формул.

Системы уравнений в вопросах А) и B) различаются количеством уравнений. Решим первое уравнение, далее найдем связь со вторым.

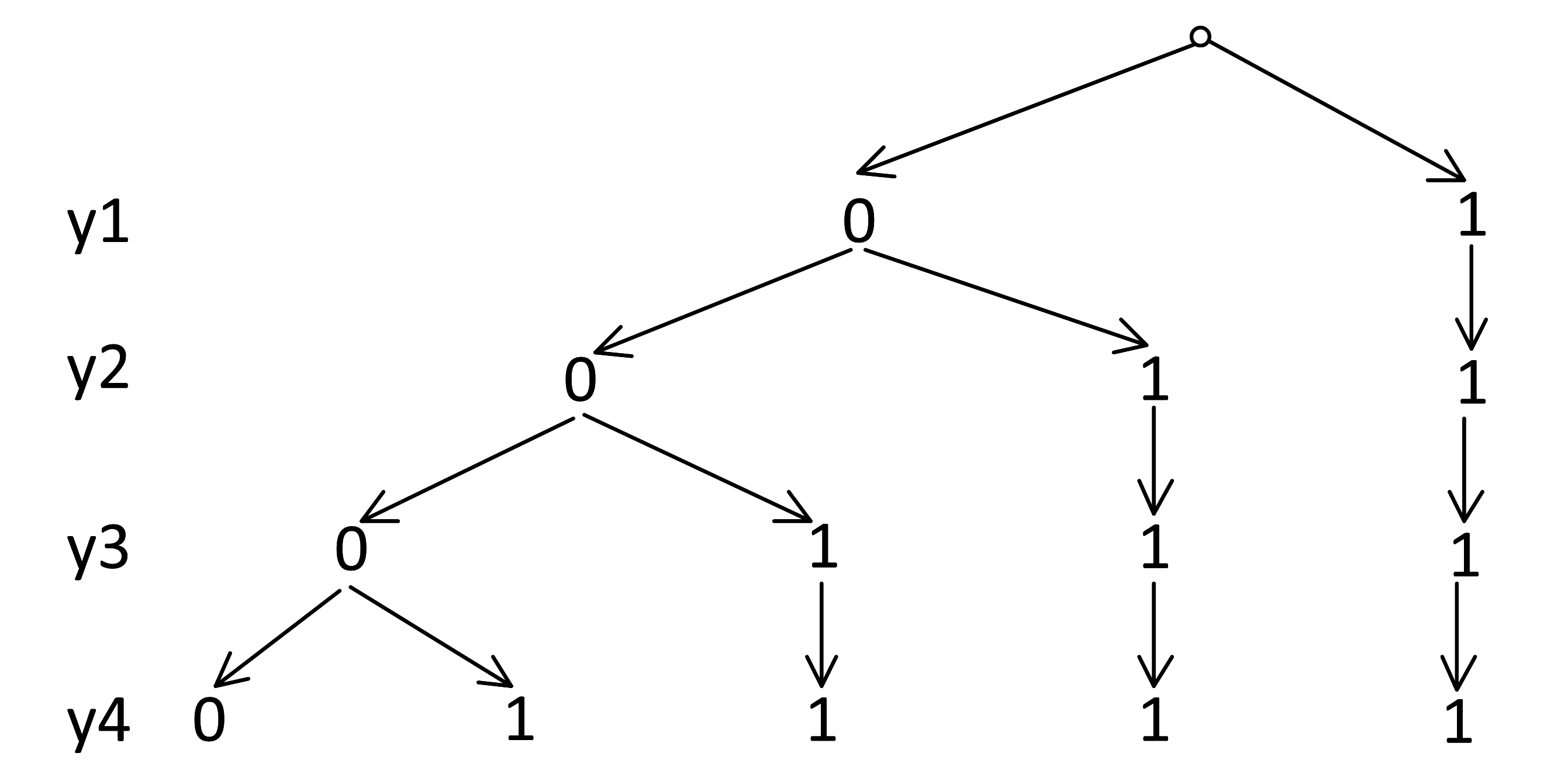
Так как переменные в уравнении все вперемежку, нужно построить тетрарное дерево. Заметим, что следование идет от переменных с большим индексом к меньшим, поэтому начнем строить дерево в обратном порядке: на верхнем уровне будут переменные x9, y9:

Для ускорения построения дерева сразу будем выводить правила.

Рассмотрим узлы 00. Подставим x9 = 0 и y9 = 0 в последнее уравнение:

(x9 → (x8 ∧ y9)) ∧ (y9 → y8) = (0 → (x8 ∧ 0)) ∧ (0 → y8) = (0 → 0) ∧ 1 = 1 ∧ 1 = 1.

Уравнение истинно всегда, независимо от значений на следующем уровне, следовательно, узлы 00 ветвятся по всем возможным веткам.

Рассмотрим узлы 01. Подставим x9 = 0 и y9 = 1 в последнее уравнение:

(0 → (x8 ∧ 1)) ∧ (1 → y8) = 1 ∧ (1 → y8) = 1 → y8 = y8

Получается, что нам подходят только узлы с y8=1. Следовательно, нам не подходят узлы 00 и 10. Остаются узлы 01 и 11:

Рассмотрим узлы 10, подставим эти значения в уравнение:

(1 → (x8 ∧ 0)) ∧ (0 → y8) = (1 → 0) ∧ 1 = 0 ∧ 1 = 0. То есть у нас ложь при любом узле-потомке. Следовательно, узлы 10 не имеют развития: 

Подумаем, есть ли смысл их рисовать дальше. На текущем уровне они вполне «живые» и умирают лишь на следующем уровне. Нам нужно посмотреть на последнее уравнение, чтобы понять, будут ли они живыми на нижнем уровне:

x1 → y1 = 1,

1 → 0 = 0.

Становится понятным, зачем дано первое уравнение, отличное от всех остальных, – чтобы не нарушались принципы построения дерева на нижнем уровне. Следовательно, эти узлы можно не принимать в расчет вообще:

Рассмотрим узлы 11, подставим эти значения в уравнение:

(1 → x8 ∧ 1)) ∧ (1 → y8) = (1 → x8) ∧ (1 → y8) = x8 ∧ y8

Уравнение будет истинным при x8=1 и y8=1. То есть узел 11 имеет только одно продолжение – 11.

Построим уровень x7, y7 по разработанным нами правилам:

Построим уровень x6, y6 по разработанным нами правилам:

Дерево становится очень большим, но мы еще не дошли и до середины. В дереве видна красота, но его расширение идет по законам, отличным от арифметической и геометрической прогрессии.

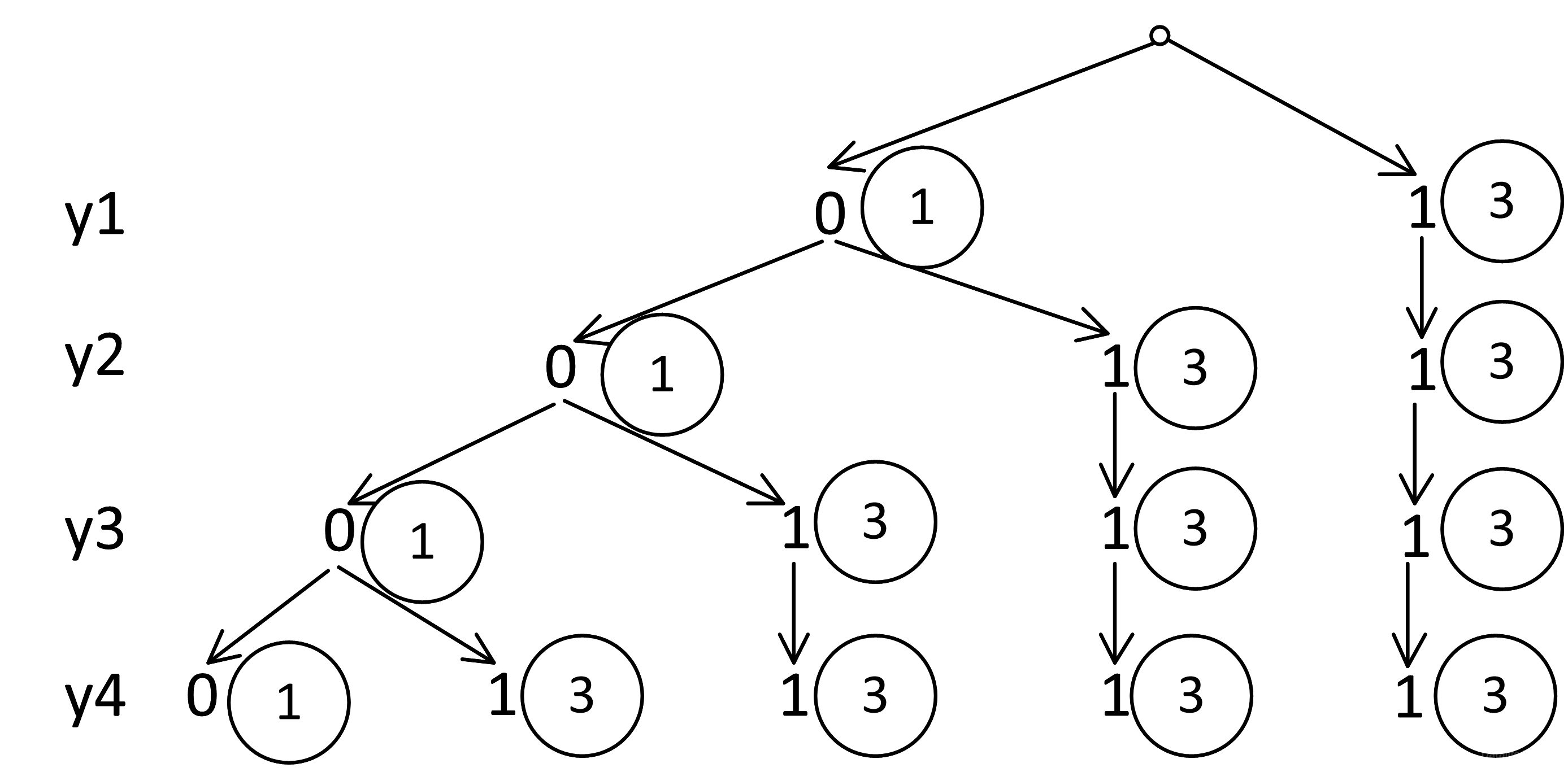
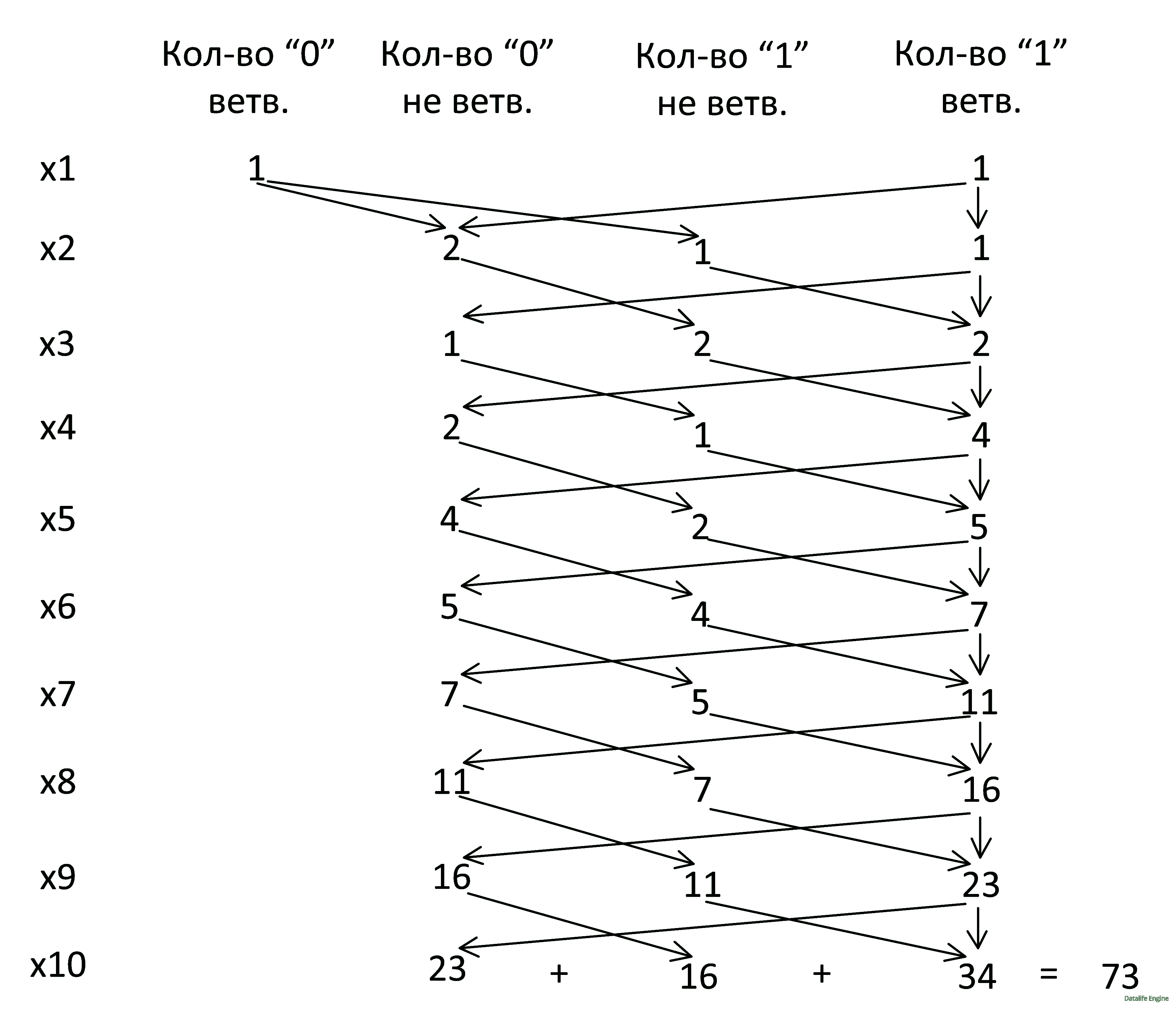
Дерево продолжать не будем, вместо него начнем строить дерево обсчета узлов разного вида, как мы это делали в задаче 4.5.6.

На первом уровне у нас по одному узлу 00, 01, 11:

Узел 00 порождает все возможные узлы:

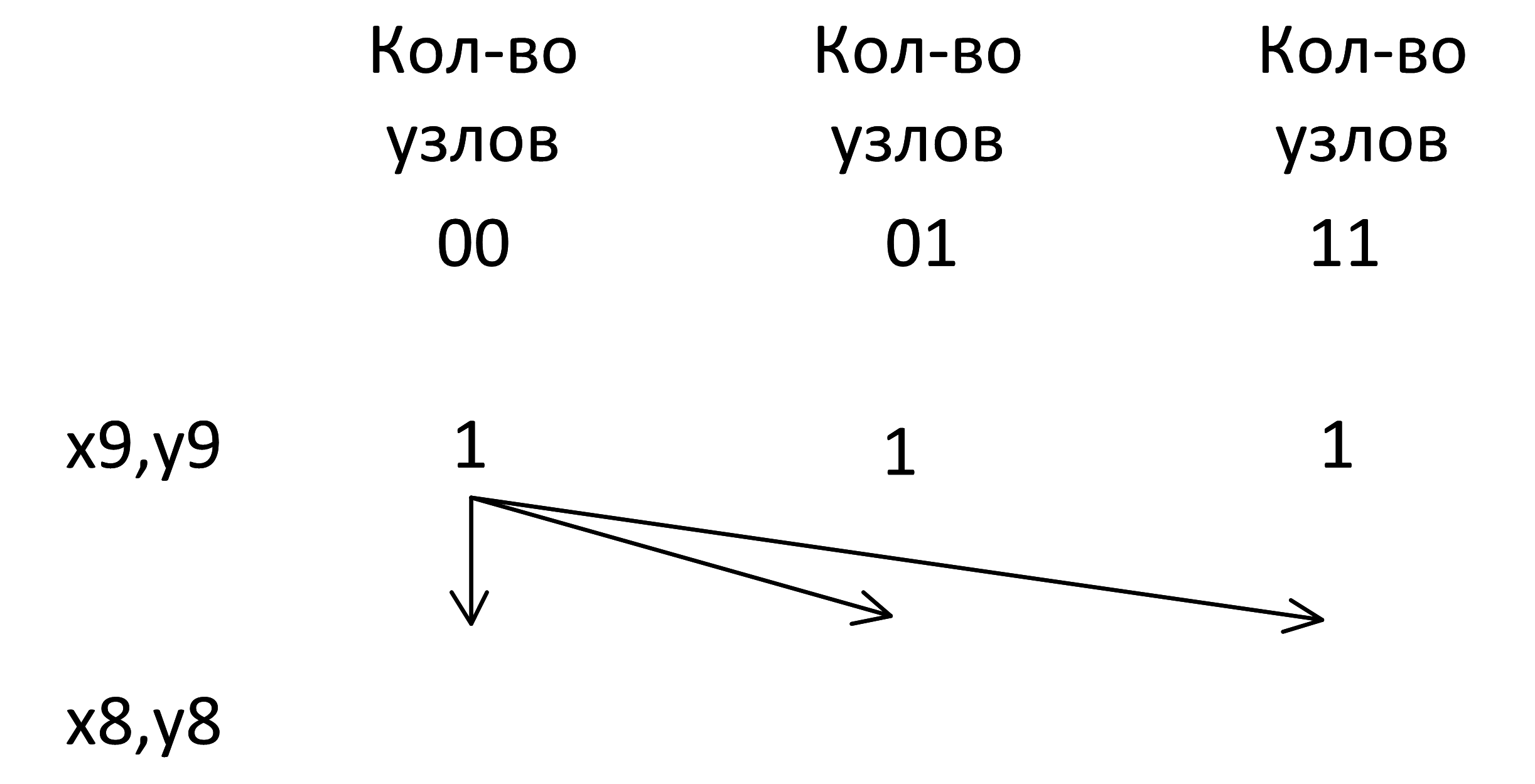
Узел 01 порождает узлы 01 и 11:

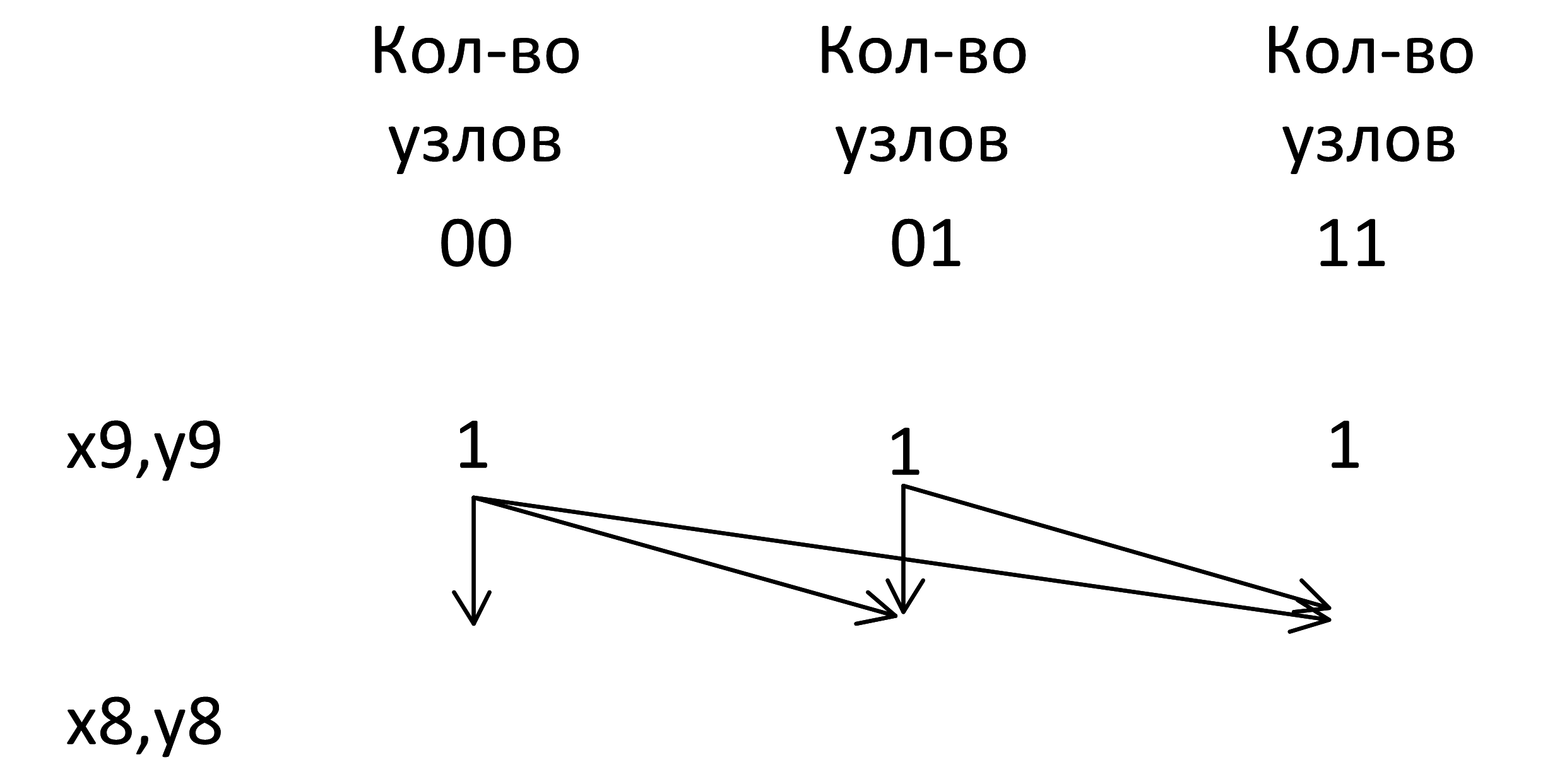
Узел 11 порождает только узел 11:

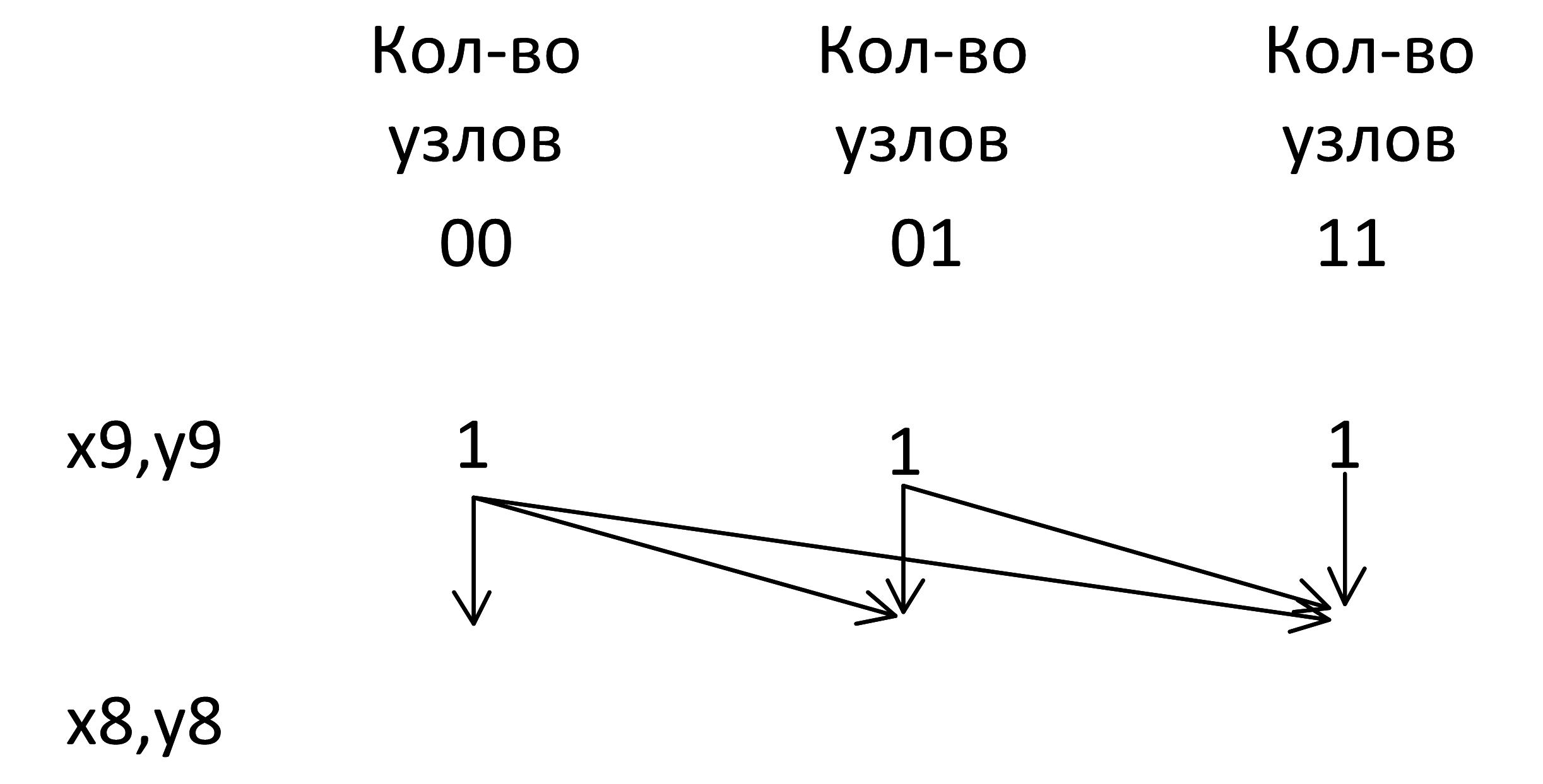
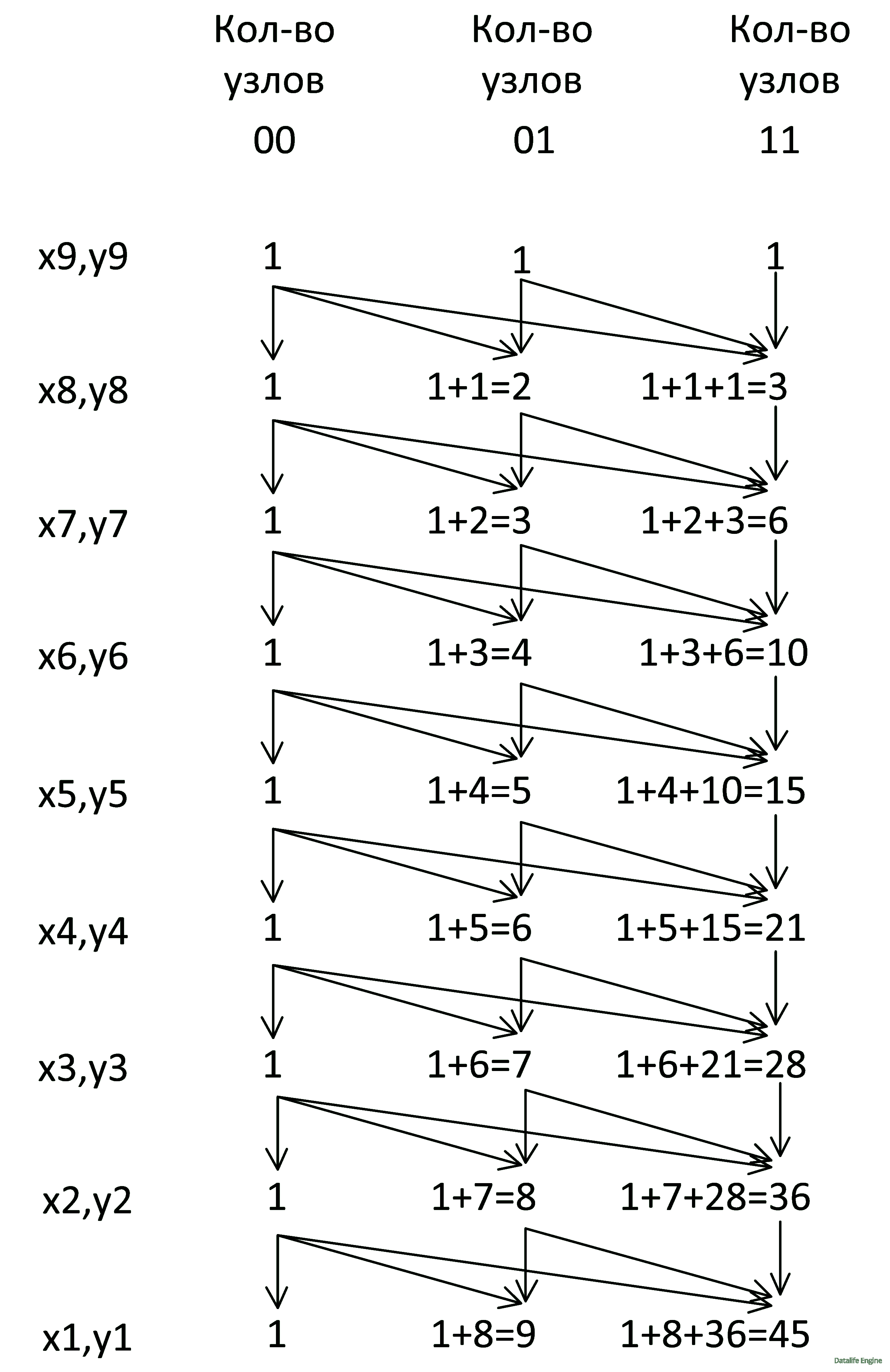
Подсчитываем количество узлов на уровне x8, y8:

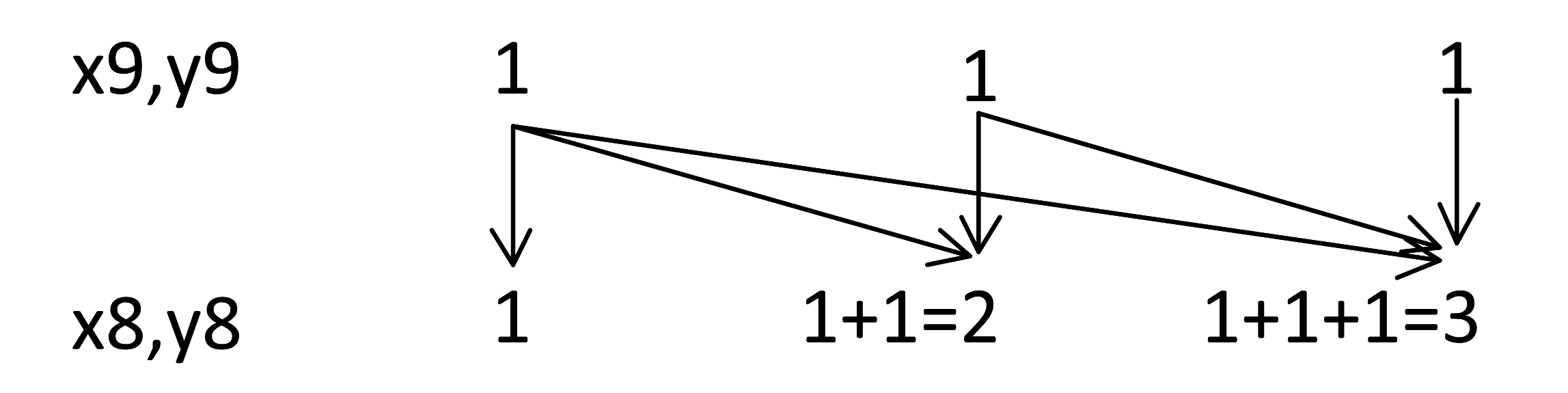
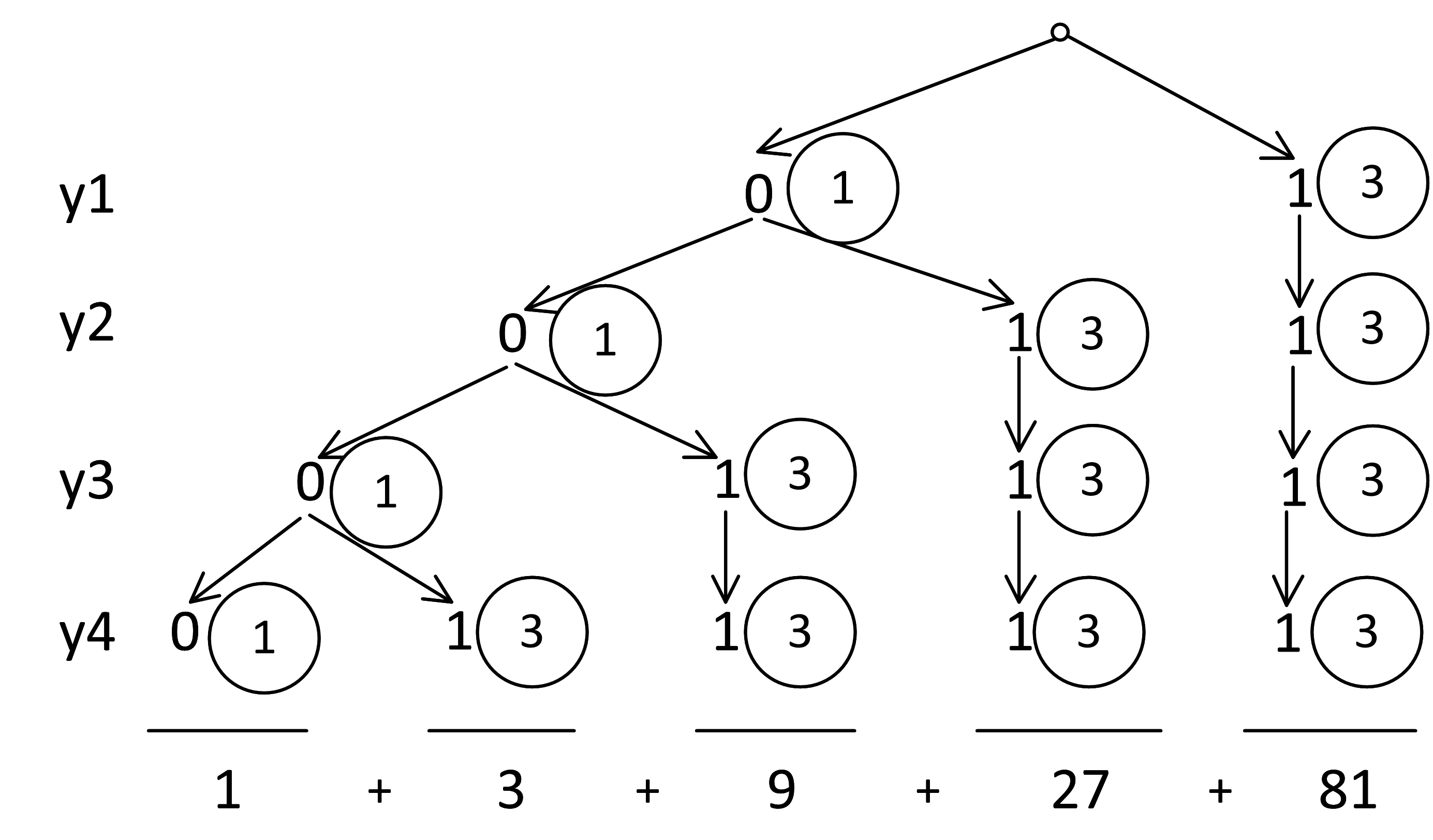
Повторяя рисунок, обсчитываем уровень x7, y7:

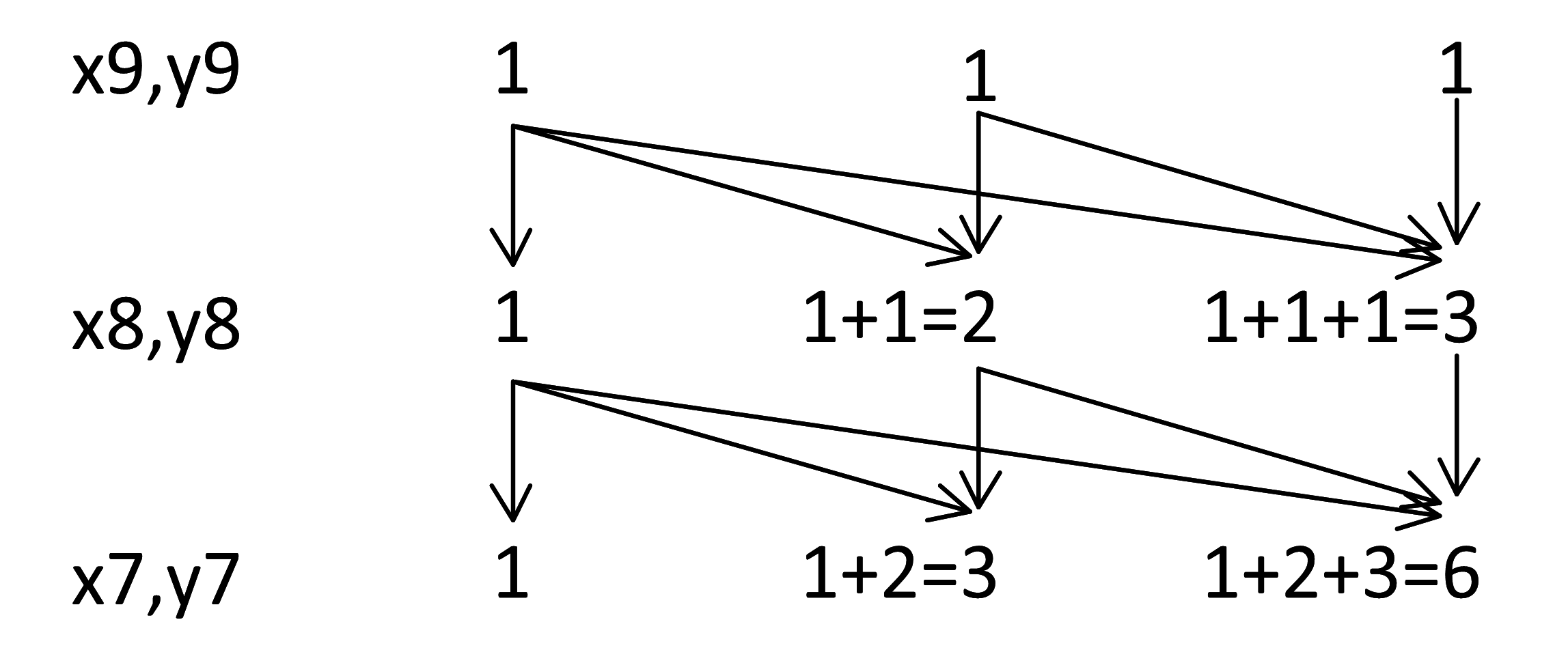
Аналогично обсчитываем все уровни:

Наконец, остается только сложить количество узлов на нижнем уровне:

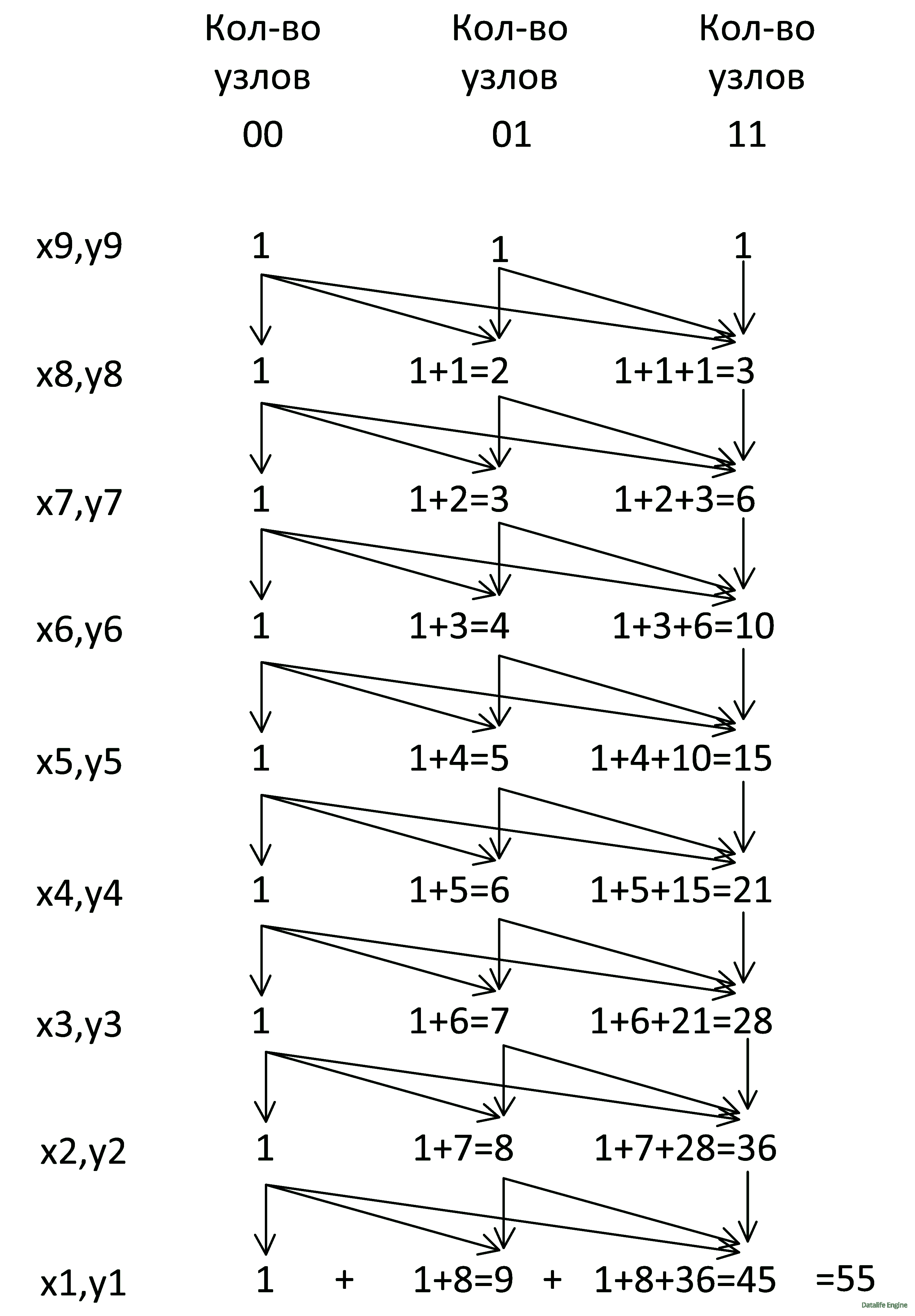
Перейдем к решению системы с увеличенным количеством уравнений. Заметим, что столбики в рекурсивном дереве соответствуют краям треугольника Паскаля. Так как ответ является суммой чисел нижнего ряда, он также находится в треугольнике Паскаля:

Так как ячейки в треугольнике Паскаля соответствуют комбинаторной функции сочетаний, подберем формулу. Пусть n – количество уравнений, тогда количество решений:

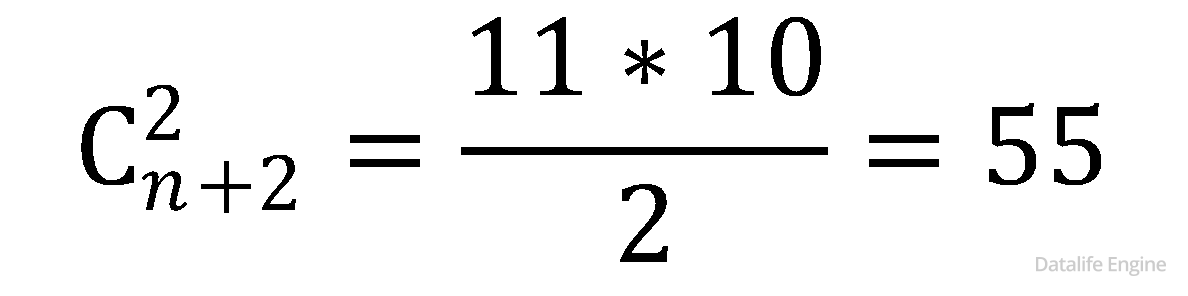
Для n = 99:

 

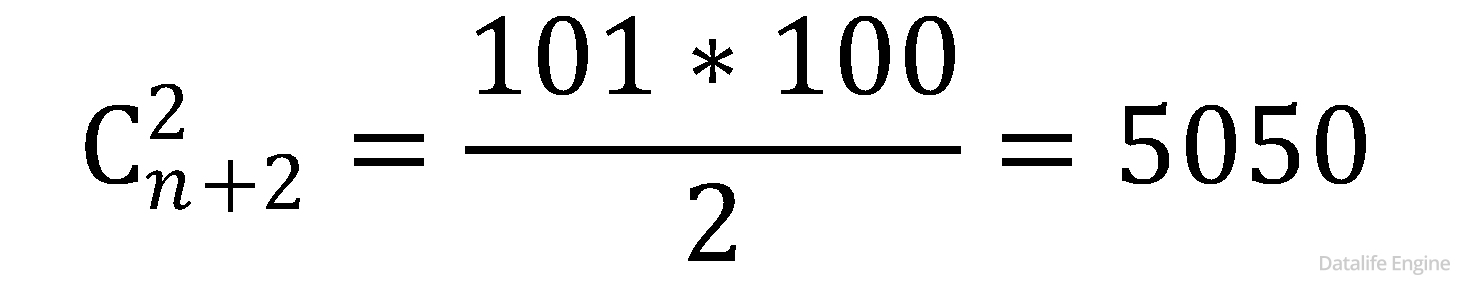
Используем новые формулы для упрощения выражений:

А → (B ∧ C) = (А → B) ∧ (А → C)

А → (B ∨ C) = (А → B) ∨ (А → C)

Докажите верность этих формул самостоятельно, составив таблицы истинности.

В нашем случае полезна формула №1. Преобразуем систему:

x1 → y1 = 1

(x2   x1) ∧(x2 → y2) ∧ (y2 → y1) = 1

(x3 → x2) ∧(x3 → y3) ∧ (y3 → y2) = 1

…

(x9 → x8) ∧ (x9 → y9) ∧ (y9 → y8) = 1

Мы получили задачу, полностью аналогичную 4.5.11А (только там следование в прямом порядке, а здесь – в обратном)!

Задача решается:

1) перекомпоновкой множителей:

(x9 → x8) ∧ … ∧ (x3 → x2) ∧ (x2 → x1) = 1

(y9 → y8) ∧ … ∧ (y3 → y2) ∧ (y2 → y1) = 1

(x9 → y9) ∧ … ∧ (x2 → y2) ∧ (x1 → y1) = 1;

2) построением двух деревьев (таблиц):

x9	0	0	0	0	0	0	0	0	0	1
x8	0	0	0	0	0	0	0	0	1	1
x7	0	0	0	0	0	0	0	1	1	1
x6	0	0	0	0	0	0	1	1	1	1
x5	0	0	0	0	0	1	1	1	1	1
x4	0	0	0	0	1	1	1	1	1	1
x3	0	0	0	1	1	1	1	1	1	1
x2	0	0	1	1	1	1	1	1	1	1
x1	0	1	1	1	1	1	1	1	1	1

 

y9	0	0	0	0	0	0	0	0	0	1
y8	0	0	0	0	0	0	0	0	1	1
y7	0	0	0	0	0	0	0	1	1	1
y6	0	0	0	0	0	0	1	1	1	1
y5	0	0	0	0	0	1	1	1	1	1
y4	0	0	0	0	1	1	1	1	1	1
y3	0	0	0	1	1	1	1	1	1	1
y2	0	0	1	1	1	1	1	1	1	1
y1	0	1	1	1	1	1	1	1	1	1

3) cоединением ветвей (столбцов) двух таблиц. Первая ветвь таблицы x (столбец) содержит одни нули, поэтому соединима со всеми ветвями y. Вторая содержит одну 1, поэтому соединима со всеми ветвями y, кроме первой, и т.д.:

x9	0	0	0	0	0	0	0	0	0	1
x8	0	0	0	0	0	0	0	0	1	1
x7	0	0	0	0	0	0	0	1	1	1
x6	0	0	0	0	0	0	1	1	1	1
x5	0	0	0	0	0	1	1	1	1	1
x4	0	0	0	0	1	1	1	1	1	1
x3	0	0	0	1	1	1	1	1	1	1
x2	0	0	1	1	1	1	1	1	1	1
x1	0	1	1	1	1	1	1	1	1	1
	10+	9+	8+	7+	6+	5+	4+	3+	2+	1+	=10(10+1)/2=55.

Для системы уравнений B) :

 

Это является суммой членов арифметической прогрессии. Пусть n - количество уравнений, тогда количество решений:

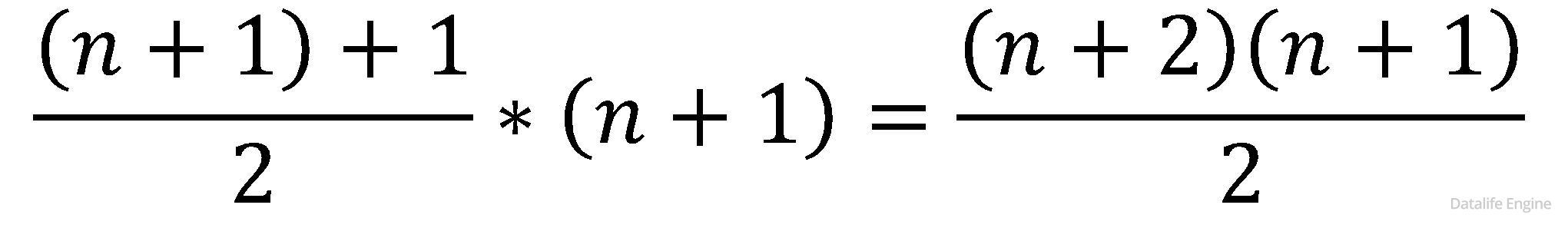
При n = 9:

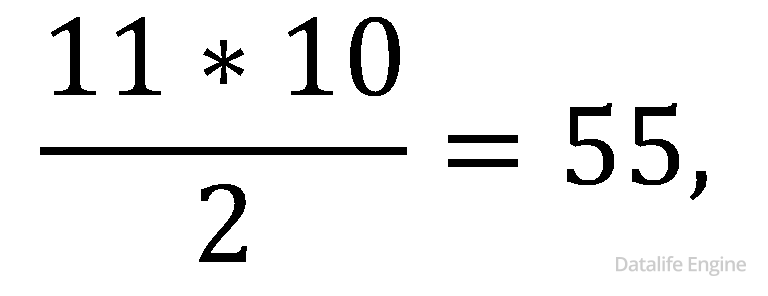
При n = 99:

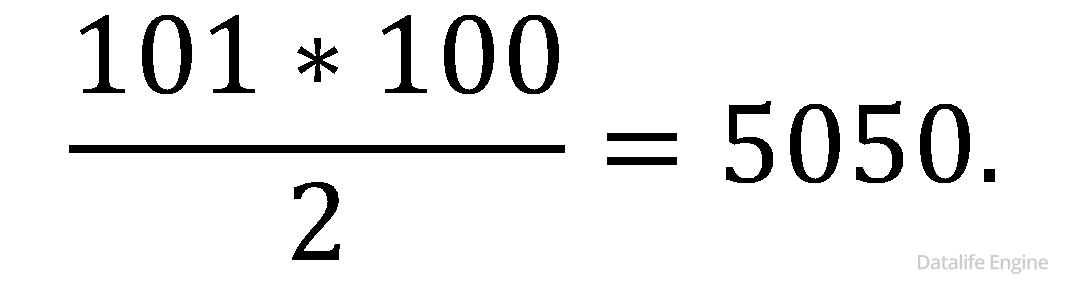
Ответ: A) 55, B) 5050