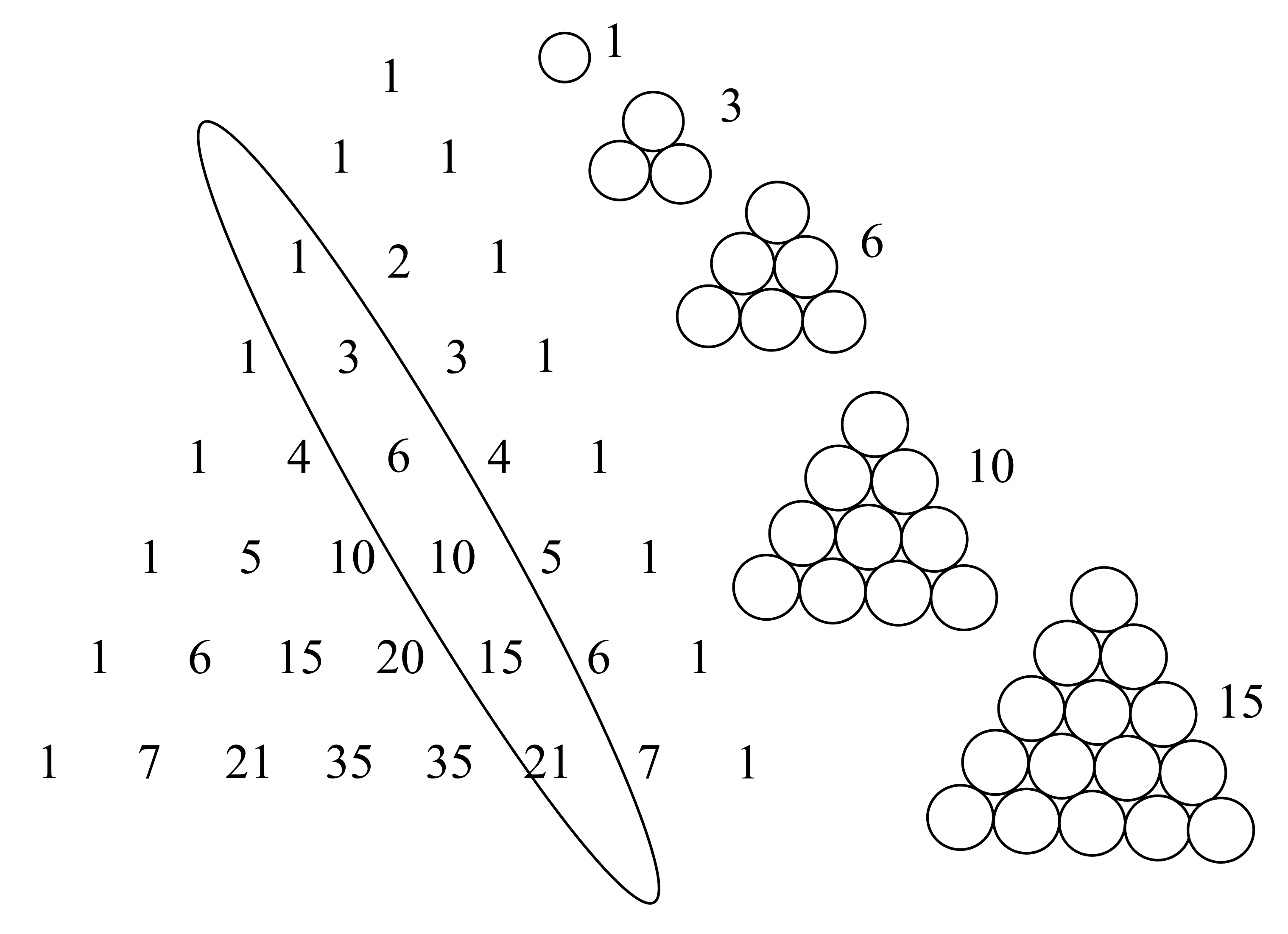В конце книги решим задачу, которую можно отнести как к комбинаторике, так и к рекурсии (во время написания книги она «гуляла» по нескольким разделам). Это сложная олимпиадная задача, которая интегрирует разные навыки, формируя находчивость. Символично то, что эта задача называется «счастливый билет».
Например, билет 4563 счастливый, так как 4 + 5 = 6 + 3.
Решим задачу при n = 4.
Посмотрим, какие вообще бывают суммы.
Минимальное значение: 0 + 0 = 0.
Максимальное значение 9 + 9 = 18.
Посчитаем, сколько есть вариантов слагаемых для всех ответов:
|
Результат
|
Варианты слагаемых
|
Количество вариантов
|
|
0
|
0+0
|
1
|
|
1
|
1+0, 0+1
|
2
|
|
2
|
2+0, 1+1, 0+2
|
3
|
|
3
|
3+0, 2+1, 1+2, 0+3
|
4
|
|
4
|
4+0, 3+1, 2+2, 1+3, 0+4
|
5
|
|
5
|
5+0, 4+1, 3+2, 2+3, 1+4, 0+5
|
6
|
|
6
|
6+0, 5+1, 4+2, 3+3, 2+4, 1+5, 0+6
|
7
|
|
7
|
7+0, 6+1, 5+2, 4+3, 3+4, 2+5, 1+6, 0+7
|
8
|
|
8
|
8+0, 7+1, 6+2, 5+3, 4+4, 3+5, 2+6, 1+7, 0+8
|
9
|
|
9
|
9+0, 8+1, 7+2, 6+3, 5+4, 4+5, 3+6, 2+7, 1+8, 0+9
|
10
|
|
10
|
9+1, 8+2, 7+3, 6+4, 5+5, 4+6, 3+7, 2+8, 1+9
|
9
|
|
11
|
9+2, 8+3, 7+4, 6+5, 5+6, 4+7, 3+8, 2+9
|
8
|
|
12
|
9+3, 8+4, 7+5, 6+6, 5+7, 4+8, 3+9
|
7
|
|
13
|
9+4, 8+5, 7+6, 6+7, 5+8, 4+9
|
6
|
|
14
|
9+5, 8+6, 7+7, 6+8, 5+9
|
5
|
|
15
|
9+6, 8+7, 7+8, 6+9
|
4
|
|
16
|
9+7, 8+8, 7+9
|
3
|
|
17
|
9+8, 8+9
|
2
|
|
18
|
9+9
|
1
|
Как посчитать количество счастливых билетов? Рассмотрим, например, варианты с результатом 2:
2 + 0, 1 + 1, 0 + 2
Справа и слева должны быть одинаковые ответы:
|
Левая часть
|
Правая часть
|
|
2+0, 1+1, 0+2
|
2+0, 1+1, 0+2
|
Мы можем соединить любой вариант слева с любым вариантом справа, получив 9 ответов:
2020
2011
2002
1120
1111
1102
0220
0211
0202
То есть мы имеем дело со степенной формулой. Осталось сложить квадраты количества вариантов:
12 + 22 + 32 + 52 + 62 + 72 + 82 + 92 + 102 + 92 + 82 + 72 + 82 + 92 + 42 + 32 + 22 + 12 =
2 * (1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 + 81) + 100 = 670
Ответ на вопрос №1: 670.
Решим задачу при n = 6.
Минимальный результат сложения цифр 0 + 0 + 0 = 0.
Максимальный результат сложения цифр 9 + 9 + 9 = 27.
По сравнению с n = 4 у нас увеличилось как количество результатов, так и количество вариантов сумм, приводящих к этому результату. Поэтому построить полную таблицу, как это мы делали при n = 4, вряд ли получится, но мы можем начать её строить, чтобы найти в ней закономерность.
0 можно получить только одним способом:
0 = 0 + 0
1 можно получить тремя способами:
1 = 1 + 0 + 0 = 0 + 1 + 0 = 0 + 0 + 1
Посмотрим, сколькими способами можно получить 2. У нас есть следующие случаи (перестановку множителей пока игнорируем):
2 + 0 + 0,
1 + 1 + 0.
Оба они дадут по три варианта с учетом перестановки множителей. Подсчет количества вариантов напоминает следующую задачу: «Сколькими способами можно разместить А по трем ячейкам, при этом А встречается ровно один раз».
В вариантах 2 + 0 + 0 А=2, а в вариантах 1 + 1 + 0 А=0
Итак, при результате, равном 2, количество вариантов равно 3 + 3 = 6.
Рассмотрим результат суммирования, равный 3. При игнорировании перестановок множителей имеем случаи:
3 + 0 + 0,
2 + 1 + 0,
1 + 1 + 1.
Случай 3 + 0 + 0, так же, как и 1 + 0 + 0, даст 3 варианта.
Случай 1 + 1 + 1 даст 1 вариант.
Осталось рассмотреть 2 + 1 + 0. Это задача на перестановки: есть три предмета, сколькими способами их можно переставить? Для первого множителя у нас есть выбор из трех вариантов, для второго – из двух (одну цифру уже израсходовали), и т.д.
Количество вариантов равно 3! = 3 * 2 * 1 = 6.
Итак, количество вариантов для результата 3 равно 3 + 6 + 1 = 10.
При продолжении подсчета количества вариантов для других результатов обратим внимание, что у нас есть всего три модели при игнорировании перестановок множителей:
|
Модель
|
Количество вариантов с учетом перестановок множителей
|
|
ААА
|
1
|
|
ABB
|
3
|
|
ABC
|
6
|
Составим табличку, как при n = 4, с учетом моделей (плюсы между слагаемыми писать не будем):
|
Результат
|
Модели
|
Общее
количество
|
|
ABB
|
Кол-во
|
ABC
|
Кол-во
|
AAA
|
Кол-во
|
|
0
|
|
1
|
|
|
000
|
1
|
1
|
|
1
|
100
|
3
|
|
|
|
|
3
|
|
2
|
200
110
|
3*2=6
|
|
|
|
|
6
|
|
3
|
300
|
3
|
210
|
6
|
111
|
1
|
3+6+2=10
|
|
4
|
400
220
211
|
3*3=9
|
310
|
6
|
|
|
9+6=15
|
|
5
|
500
311
221
|
3*3=9
|
410
320
|
6*2=12
|
|
|
9+12=21
|
Уже для результата 5 мы столкнулись с проблемой, как бы не упустить какой-нибудь случай. Далее сложность будет только возрастать. Для случая n = 4 была видна закономерность: с увеличением результата на 1 количество вариантов сперва возрастало на 1, затем убывало на 1.
Попробуем найти закономерность в последовательности 1, 3, 6, 10, 15, 21. Вычислим приращение:
|
Результат
|
Количество вариантов
|
Приращение
|
|
0
|
1
|
|
|
1
|
3
|
2
|
|
2
|
6
|
3
|
|
3
|
10
|
4
|
|
4
|
15
|
5
|
|
5
|
21
|
6
|
Очевидно, далее приращение будет увеличиваться на 1. Но в какой-то момент начнется убыль так же, как это было и при n = 4.
Если мы начнем рассматривать конечные результаты, то увидим, что:
для получения результата 27 есть только один вариант -
9 + 9 + 9 = 27;
для получения 26 вариант без учета перестановок -
9 + 9 + 8;
Для получения 25 варианты без учета перестановок:
9 + 9 + 7,
9 + 8 + 8.
То есть таблица с количеством вариантов полностью симметрична – возрастает при изменении результата от 0 до 13, затем убывает от 14 до 27. Причем количество вариантов от 0 до 13 равно количеству вариантов от 14 до 0.
Для скорости построим её с помощью excel:
|
Результат
|
Приращение
|
Количество вариантов
|
квадрат количества вариантов
|
|
0
|
1
|
1
|
1
|
|
1
|
2
|
3
|
9
|
|
2
|
3
|
6
|
36
|
|
3
|
4
|
10
|
100
|
|
4
|
5
|
15
|
225
|
|
5
|
6
|
21
|
441
|
|
6
|
7
|
28
|
784
|
|
7
|
8
|
36
|
1296
|
|
8
|
9
|
45
|
2025
|
|
9
|
10
|
55
|
3025
|
|
10
|
11
|
66
|
4356
|
|
11
|
12
|
78
|
6084
|
|
12
|
13
|
91
|
8281
|
|
13
|
14
|
105
|
11025
|
|
Сумма:
|
|
|
37688
|
|
Счастливых билетов
|
|
|
75376
|
Ответ на вопрос №2: 75376
Продолжим решать задачу для n = 4. Попробуем решить её в общем случае. Заметим, что приращение при n = 3 совпадает с количеством вариантов при n = 2. То есть мы можем предположить, что количество вариантов при n = 3 – это приращение при n = 4.
Проверим, какое же приращение имеет задача при n = 2 и какой у этого физический смысл.
|
Результат
|
Количество вариантов
|
Приращение
|
|
0
|
1
|
|
|
1
|
2
|
1
|
|
2
|
3
|
1
|
|
3
|
4
|
1
|
|
4
|
5
|
1
|
|
5
|
6
|
1
|
|
6
|
7
|
1
|
|
7
|
8
|
1
|
|
8
|
9
|
1
|
|
9
|
10
|
1
|
По идее, это приращение является количеством вариантов при подсчете счастливых билетов при n = 2. Выпишем счастливые билеты при n = 2:
00,
11,
22,
33,
44,
55,
66,
77,
88,
99.
Билет из двух цифр счастливый, если эти цифры совпадают. Так и есть, мы получили 1 у каждого значения результата. Наше подозрение, что количество вариантов при n-1 – это приращение при количестве вариантов n, превращается в уверенность.
Теперь с помощью excel подсчет вариантов становится быстрым.
При n = 2:
|
Результат
|
Вариантов при n=2
|
квадрат количества вариантов
|
|
0
|
1
|
1
|
|
1
|
1
|
1
|
|
2
|
1
|
1
|
|
3
|
1
|
1
|
|
4
|
1
|
1
|
|
5
|
1
|
1
|
|
6
|
1
|
1
|
|
7
|
1
|
1
|
|
8
|
1
|
1
|
|
9
|
1
|
1
|
|
Счастливых билетов
|
|
10
|
При n = 4:
|
Результат
|
Вариантов при n=2
|
Вариантов при n=4
|
квадрат количества вариантов
|
|
0
|
1
|
1
|
1
|
|
1
|
1
|
2
|
4
|
|
2
|
1
|
3
|
9
|
|
3
|
1
|
4
|
16
|
|
4
|
1
|
5
|
25
|
|
5
|
1
|
6
|
36
|
|
6
|
1
|
7
|
49
|
|
7
|
1
|
8
|
64
|
|
8
|
1
|
9
|
81
|
|
9
|
1
|
10
|
100
|
|
Счастливых билетов
|
|
|
670
|
При n = 6:
|
Результат
|
Вариантов при n=2
|
Вариантов при n=4
|
Вариантов при n=6
|
квадрат количества вариантов
|
|
0
|
1
|
1
|
1
|
1
|
|
1
|
1
|
2
|
3
|
9
|
|
2
|
1
|
3
|
6
|
36
|
|
3
|
1
|
4
|
10
|
100
|
|
4
|
1
|
5
|
15
|
225
|
|
5
|
1
|
6
|
21
|
441
|
|
6
|
1
|
7
|
28
|
784
|
|
7
|
1
|
8
|
36
|
1296
|
|
8
|
1
|
9
|
45
|
2025
|
|
9
|
1
|
10
|
55
|
3025
|
|
10
|
1
|
11
|
66
|
4356
|
|
11
|
1
|
12
|
78
|
6084
|
|
12
|
1
|
13
|
91
|
8281
|
|
13
|
1
|
14
|
105
|
11025
|
|
Счастливых билетов
|
|
|
|
75376
|
При n = 8:
|
Результат
|
Вариантов при n=2
|
Вариантов при n=4
|
Вариантов при n=6
|
Вариантов при n=8
|
квадрат количества вариантов
|
|
0
|
1
|
1
|
1
|
1
|
1
|
|
1
|
1
|
2
|
3
|
4
|
16
|
|
2
|
1
|
3
|
6
|
10
|
100
|
|
3
|
1
|
4
|
10
|
20
|
400
|
|
4
|
1
|
5
|
15
|
35
|
1225
|
|
5
|
1
|
6
|
21
|
56
|
3136
|
|
6
|
1
|
7
|
28
|
84
|
7056
|
|
7
|
1
|
8
|
36
|
120
|
14400
|
|
8
|
1
|
9
|
45
|
165
|
27225
|
|
9
|
1
|
10
|
55
|
220
|
48400
|
|
10
|
1
|
11
|
66
|
286
|
81796
|
|
11
|
1
|
12
|
78
|
364
|
132496
|
|
12
|
1
|
13
|
91
|
455
|
207025
|
|
13
|
1
|
14
|
105
|
560
|
313600
|
|
15
|
1
|
16
|
136
|
816
|
665856
|
|
16
|
1
|
17
|
153
|
969
|
938961
|
|
17
|
1
|
18
|
171
|
1140
|
1299600
|
|
18
|
1
|
19
|
190
|
1330
|
1768900
|
|
Счастливых билетов
|
|
|
|
|
10176286
|
При подсчете количества счастливых билетов учтите, что не всегда нужно складывать квадраты и удваивать. Иногда центральный результат единственный, как в случае n = 8. В нём мы удваиваем все полученные квадраты от 1 до 1299600 и прибавляем 1768900 в одном экземпляре.
Ответ на вопрос №3: 10176286.
Если мы вспомним задачи на подсчет количества программ (например, 3.2.9: из одного числа получить другое при операциях +1 и +2), то мы решали их тремя методами: графовым, комбинаторным и рекурсивным. Подумаем, можно ли нашу нынешнюю задачу решить полностью комбинаторным методом.
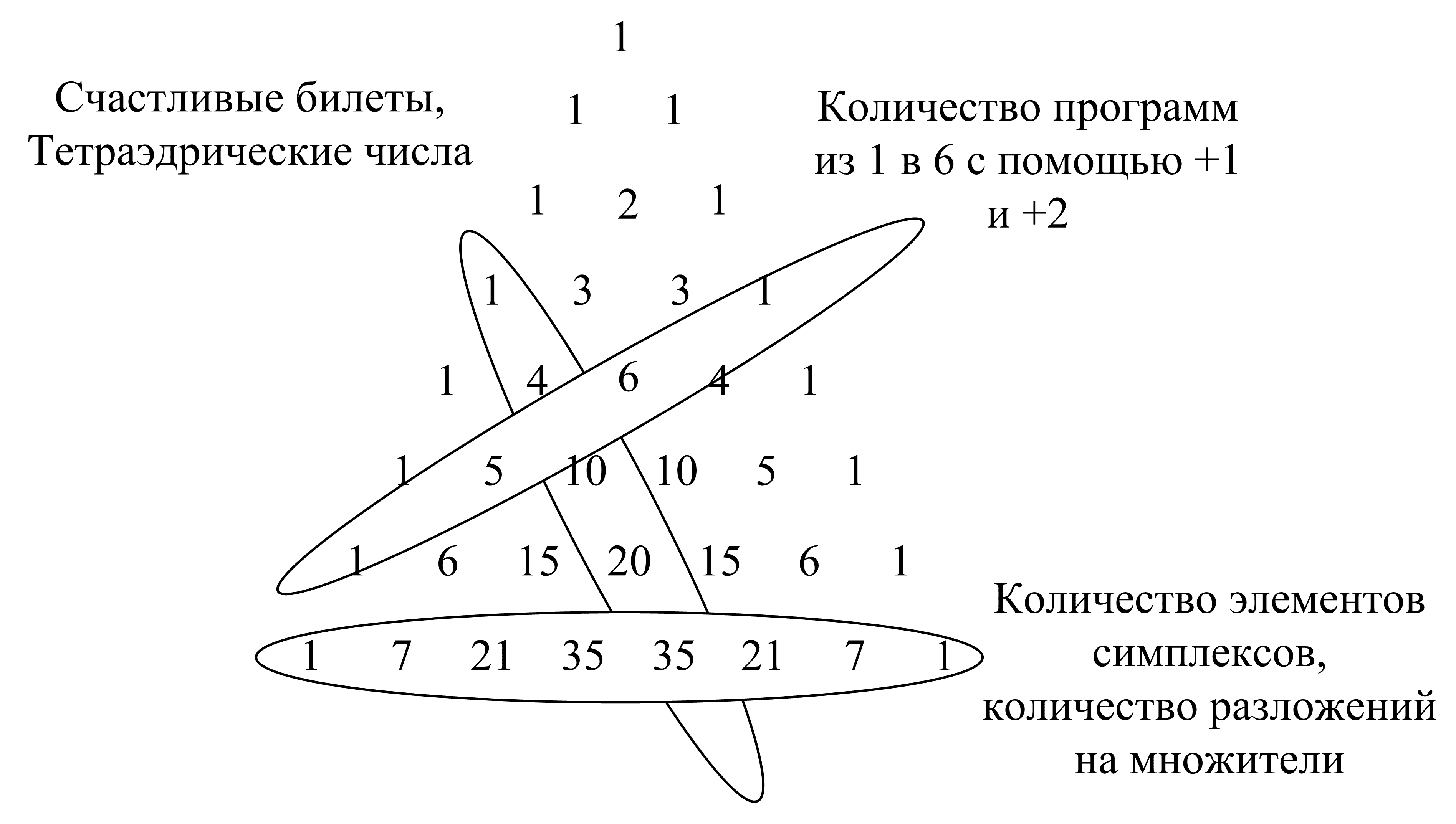
Если мы посмотрим на столбцы в последней заполненной нами таблице, то мы увидим числа, очень нам знакомые по комбинаторным задачам. Это же числа из треугольника Паскаля! Сравните:
Такие числа зазываются треугольными.
Числа из следующего среза – это количество пирамидок (тетраэдров), которые мы можем сложить из шаров. Поэтому эти числа называются тетраэдрическими.
В целом же комбинаторика – большой и увлекательный раздел математики. Решая дополнительные задачи из этого приложения, мы освоили ряд исследовательских приемов, развив навыки, которые нужны на тот случай, если в ЕГЭ попадется задача нового типа, которую мы еще не прорешивали.