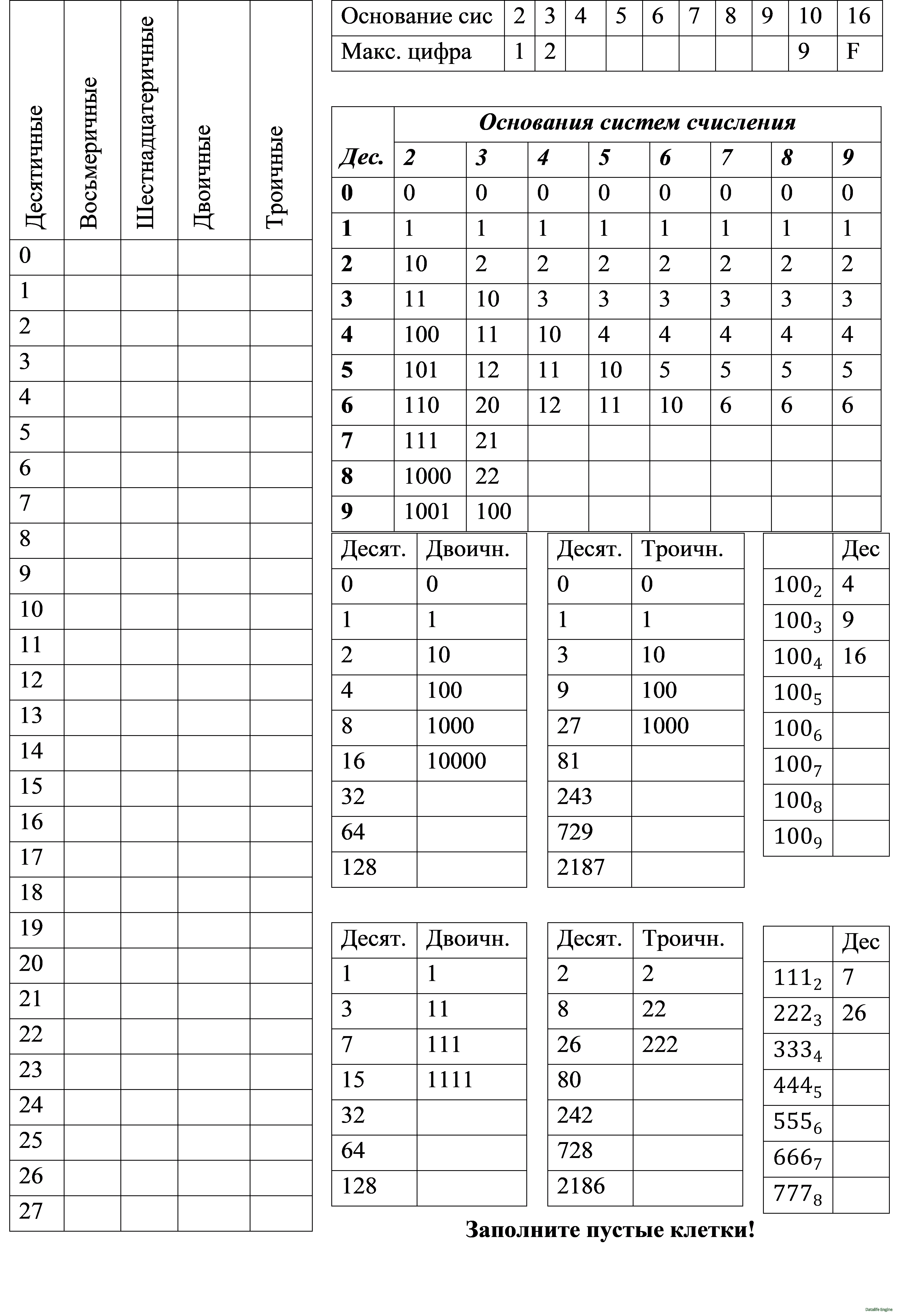
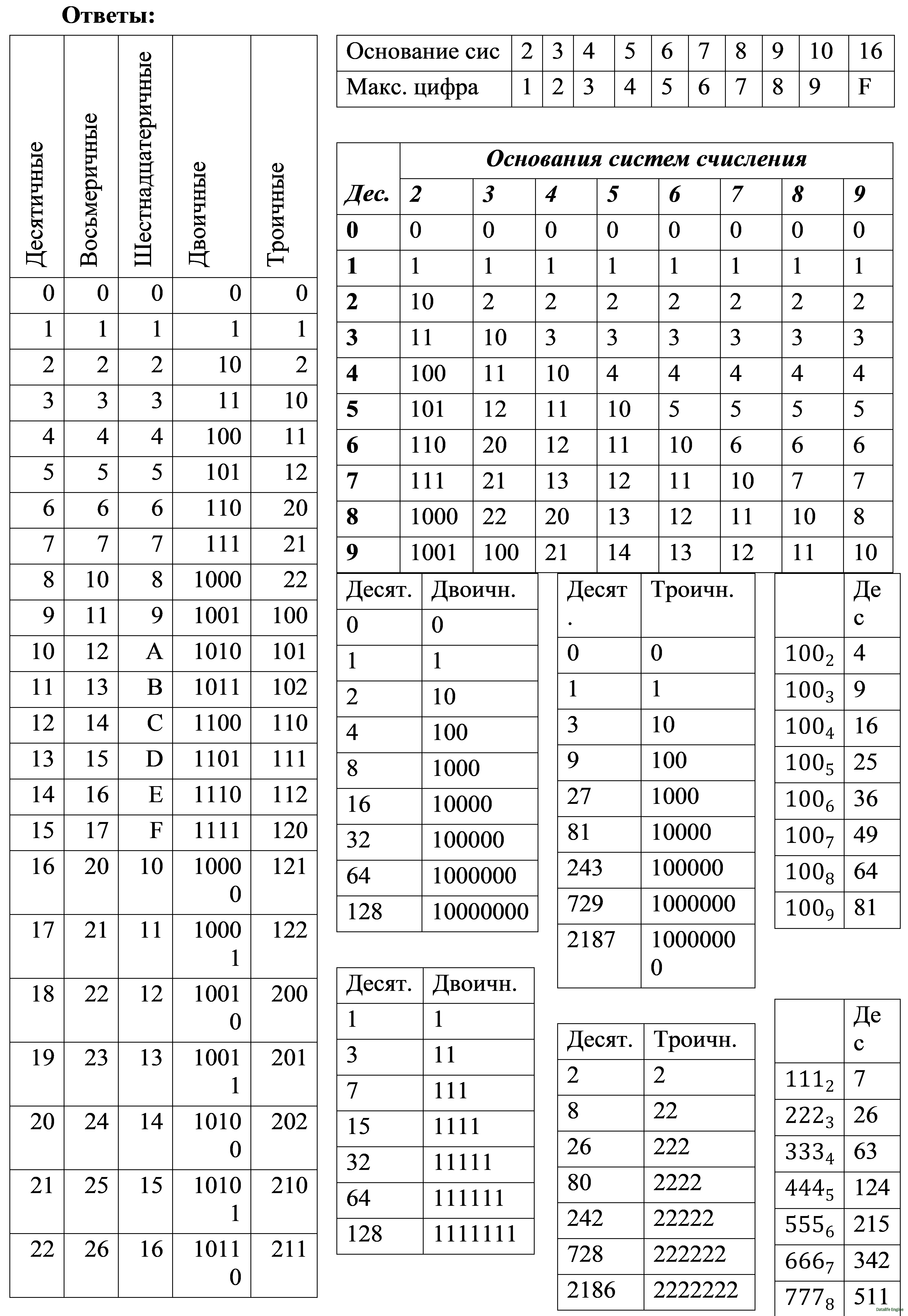
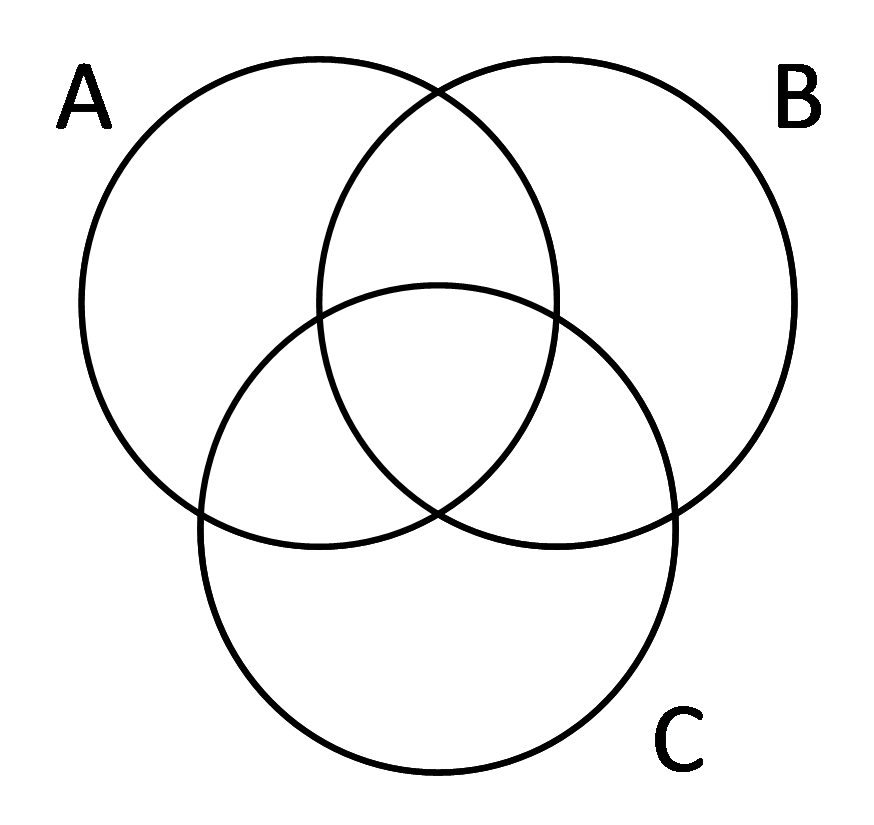
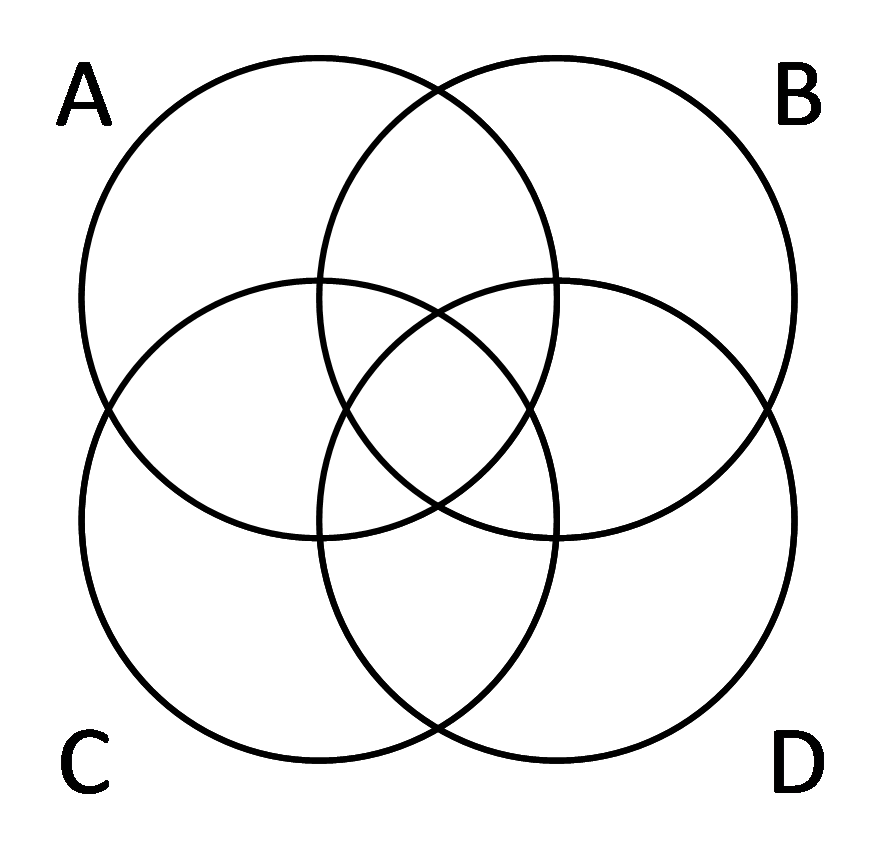
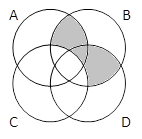
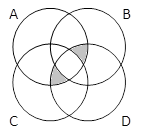
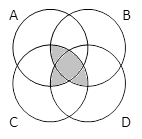
B. Тренировка решения задач на круги Эйлера
1) Закрасьте области, соответствующие выражениям:
|
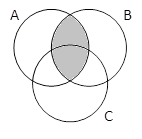
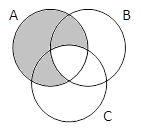
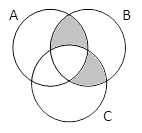
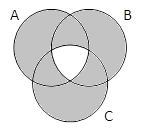
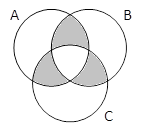
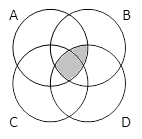
A & B |
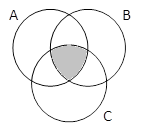
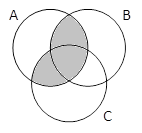
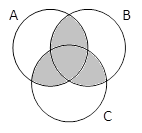
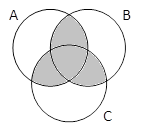
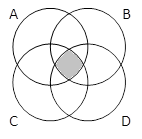
A & B & C |
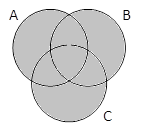
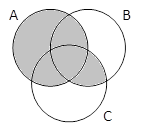
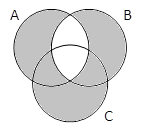
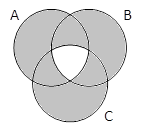
A | B | C
|
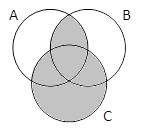
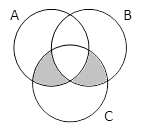
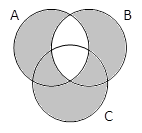
A & B | C
|
|
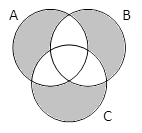
A | B & C
|
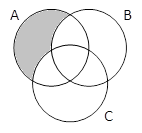
A & ⌐(B | C)
|
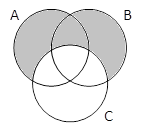
(A | B) & ⌐C
|
A & ⌐(B & C)
|
|
A & B | A & C
|
A&B | A&C | B&C
|
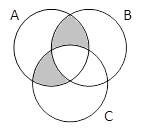
A & (B | C) & ⌐(B&C)
|
B & (A | C) & (⌐A | ⌐C) |
|
(C&A | C&B) & ⌐ (A&B)
|
(A | B | C) & ⌐(A & B)
|
(A | B | C) & ⌐(A & B & C)
|
(A&B | A&C | B&C) & ⌐( A & B & C)
|
|
(A | B | C) & (⌐A | ⌐B | ⌐C)
|
(A | B | C) & (⌐A | ⌐B)
|
(A | B | C) & ⌐(A&B | A&C | B&C)
|
(A | B | C) & ( ⌐(A | B | C) | (A&B | A&C | B&C))
|
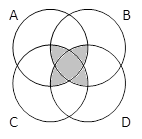
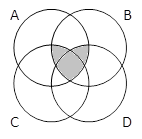
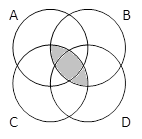
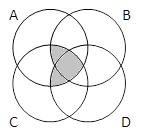
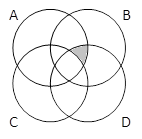
2) Закрасьте области, соответствующие выражениям:
|
A & B & C & D |
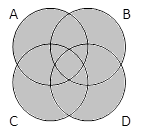
A | B | C | D
|
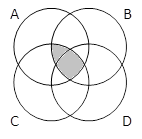
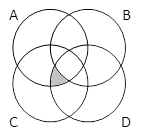
A & B & C |
|
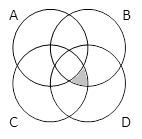
(A & B) & (B & D)
|
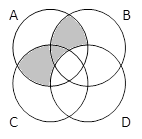
A & D | B & C
|
A & B & C | A & B & D
|
|
B & (A & C | C & D)
|
A & C & (B | D)
|
(A & B & D) & ⌐C
|
|
(A & C & D)& ⌐(A & B)
|
(B & C & D) & ⌐(A & B & C)
|
(A & B | A & C) & ⌐D
|
|
B & (A | D) & ⌐C |
((A & B & D) | (A & C & D)) & ⌐(B & C)
|
B & C | A & D & ⌐(B & D) |
Ответы 1:
|
A & B
|
A & B & C
|
A | B | C
|
A & B | C
|
|
A | B & C
|
A & ⌐(B | C)
|
(A | B) & ⌐C
|
A & ⌐(B & C)
|
|
A & B | A & C
|
A&B | A&C | B&C
|
A & (B | C) & ⌐(B&C)
|
B & (A | C) & (⌐A | ⌐C)
|
|
(C&A | C&B) & ⌐ (A&B)
|
(A | B | C) & ⌐(A & B)
|
(A | B | C) & ⌐(A & B & C)
|
(A&B | A&C | B&C) & ⌐( A & B & C)
|
|
(A | B | C) & (⌐A | ⌐B | ⌐C)
|
(A | B | C) & (⌐A | ⌐B)
|
(A | B | C) & ⌐(A&B | A&C | B&C)
|
(A | B | C) & ( ⌐(A | B | C) | (A&B | A&C | B&C))
|
Ответы 2:
|
A & B & C & D
|
A | B | C | D
|
A & B & C
|
|
(A & B) & (B & D)
|
A & D | B & C
|
A & B & C | A & B & D
|
|
B & (A & C | C & D)
|
A & C & (B | D)
|
(A & B & D) & ⌐C
|
|
(A & C & D)& ⌐(A & B)
|
(B & C & D) & ⌐(A & B & C)
|
(A & B | A & C) & ⌐D
|
|
B & (A | D) & ⌐C
|
((A & B & D) | (A & C & D)) & ⌐(B & C)
|
B & C | A & D & ⌐(B & D)
|
С. Обзор приемов для решения логических уравнений
Тема «логические уравнения» является одной из самых сложных, поэтому легко растеряться от большого количества задач. Сделаем обзор приемов, использующихся при решении задач на логические уравнения.
Основными приемами являются (в задаче не обязательно присутствуют все три приема):
- упрощение выражения;
- введение новых обозначений:
- построение дерева.
Признаком того, что выражение нужно упрощать, является повторение одного и того же набора переменных в слегка различающихся выражениях, соединенных между собой, например:
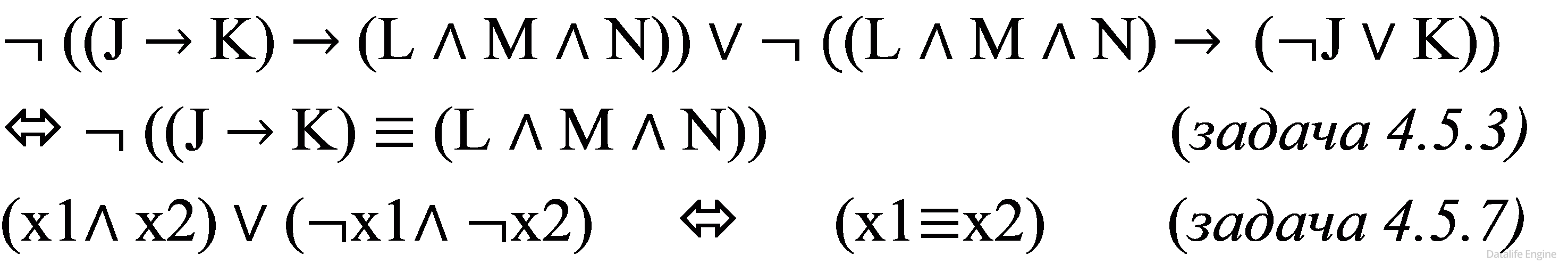
Упрощение делается по формулам, или, если их не хватает, с помощью составления таблицы истинности.
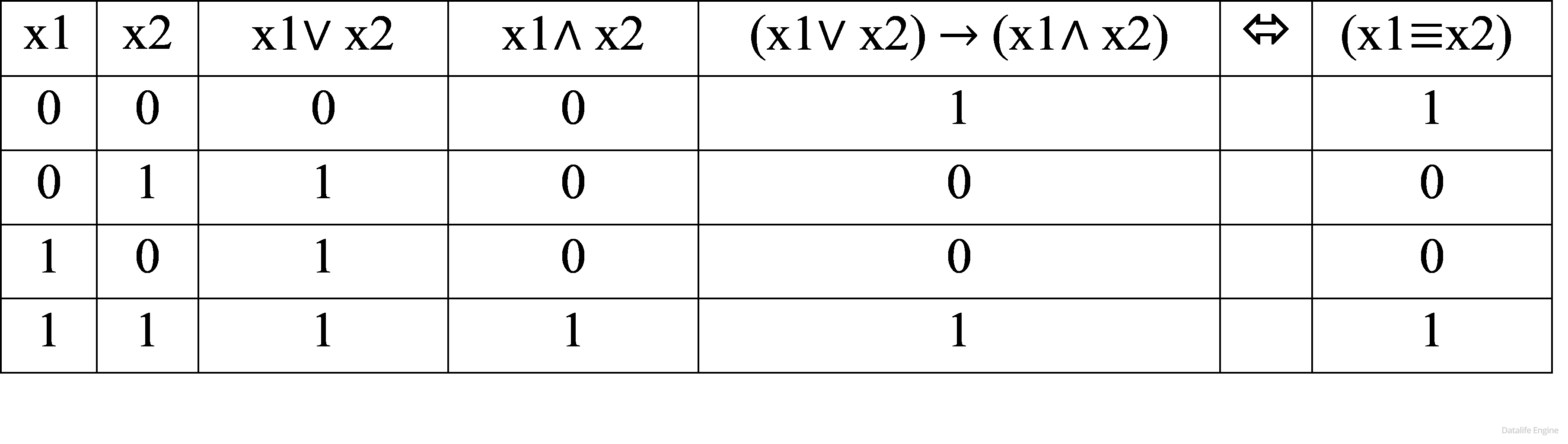
Упрощение выражений нужно не всегда. Сравните случаи, когда нужно упрощать, а когда – нет:
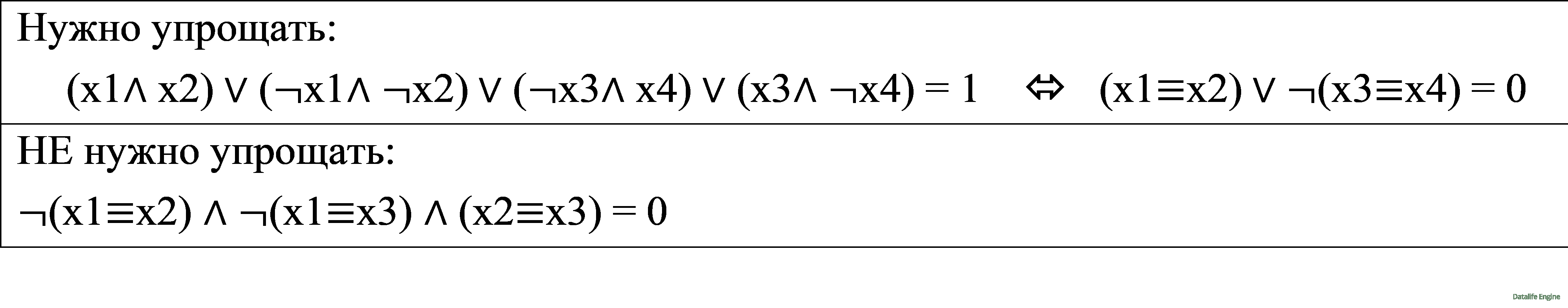
Новые обозначения вводятся в тех же случаях, что и в математике, когда есть повторяющиеся фрагменты выражений, причем наборы переменных в этих выражениях изолированы друг от друга. Сравните:
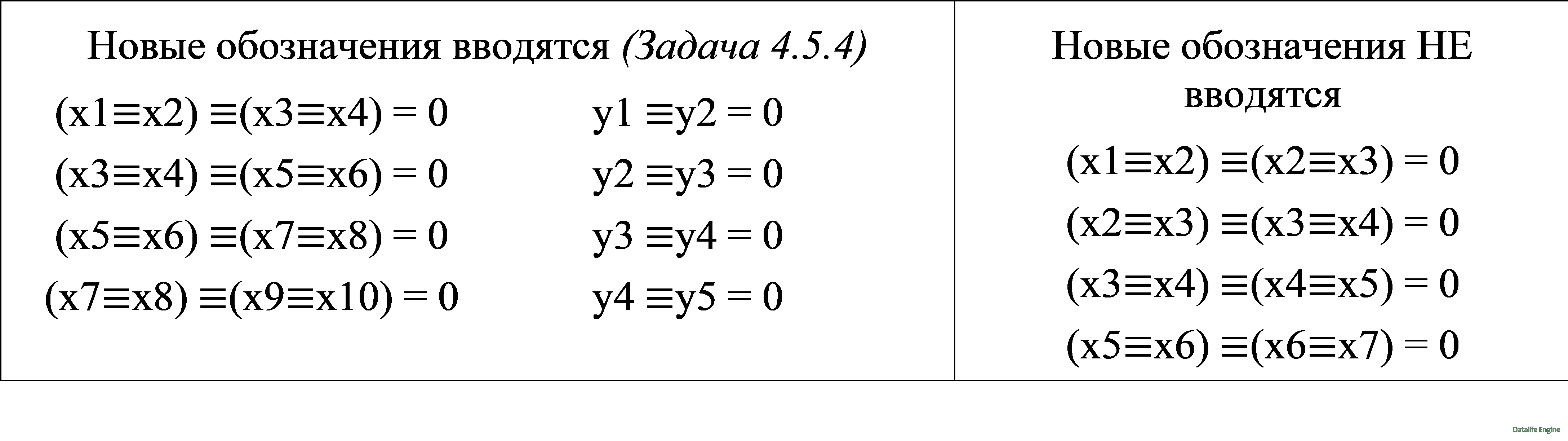
Этапы «Упрощение выражения» и «Введение новых обозначений» могут чередоваться, дерево строится как предпоследний этап:

При введении новых обозначений строится дерево уже в новых переменных. При возвращении к исходным переменным для каждого вида узлов дерева подсчитывается количество решений в исходных переменных, по каждой ветке результаты перемножаются, затем подводится итог путем сложения.
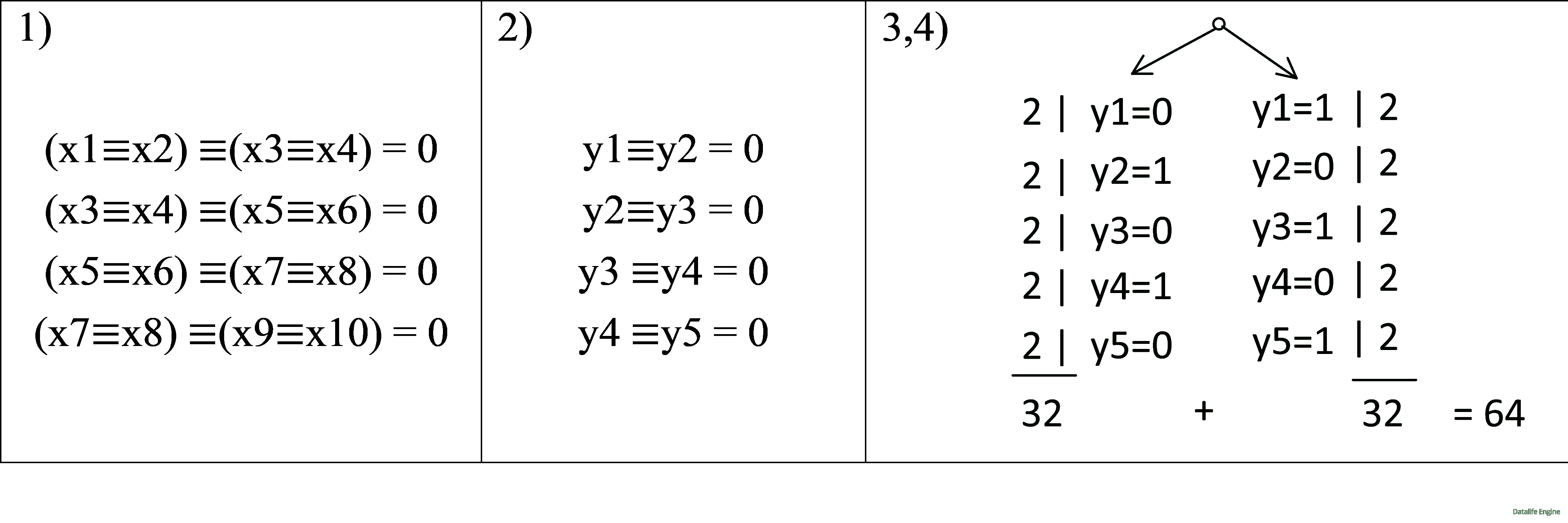
Примечание. 1) Иногда дерево целесообразно строить в обратном порядке (от переменной с бОльшим индексом к переменной с меньшим индексом). См. задачу 4.5.13.
2) Иногда на нижнем уровне дерево «ведет себя по-другому», особенно когда есть «умирающие» ветки. См. задачу 4.5.8.
Задачи с большими деревьями
Иногда дерево получается очень большим. Тогда нужно в нем найти закономерность. Возможны три случая:
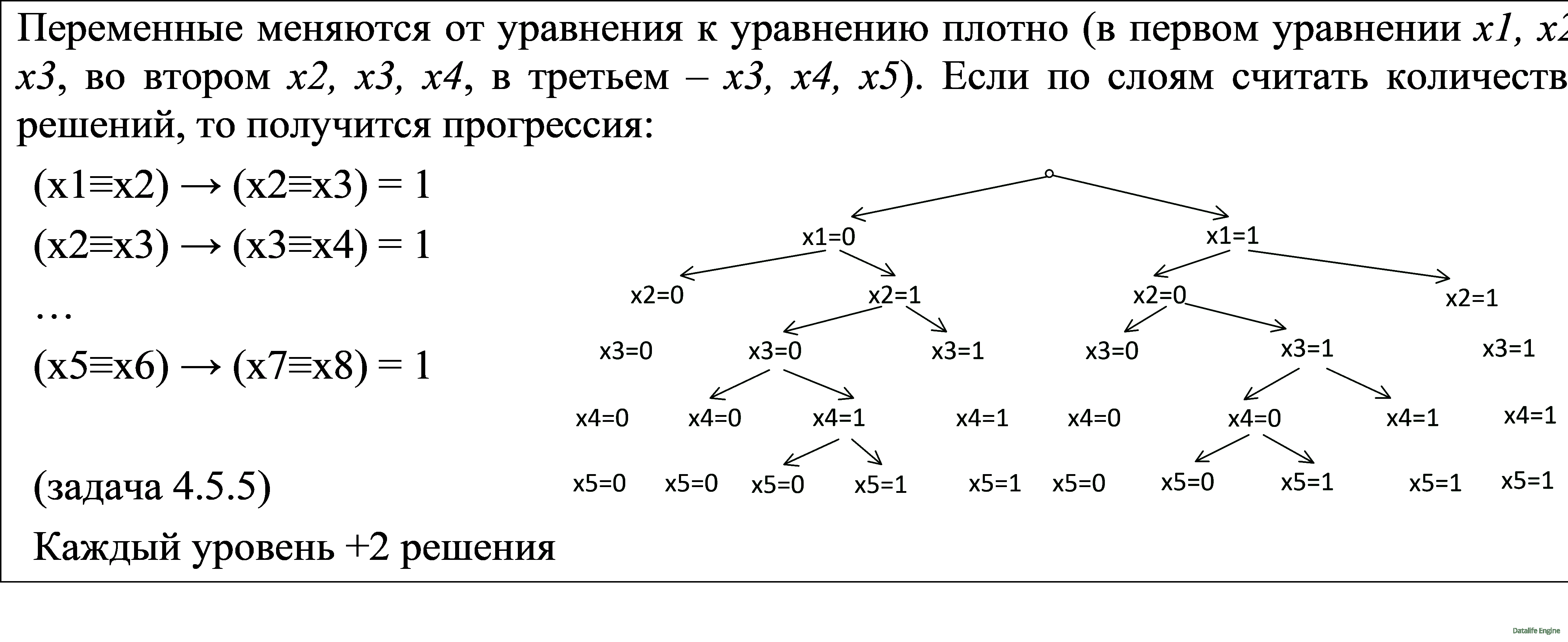
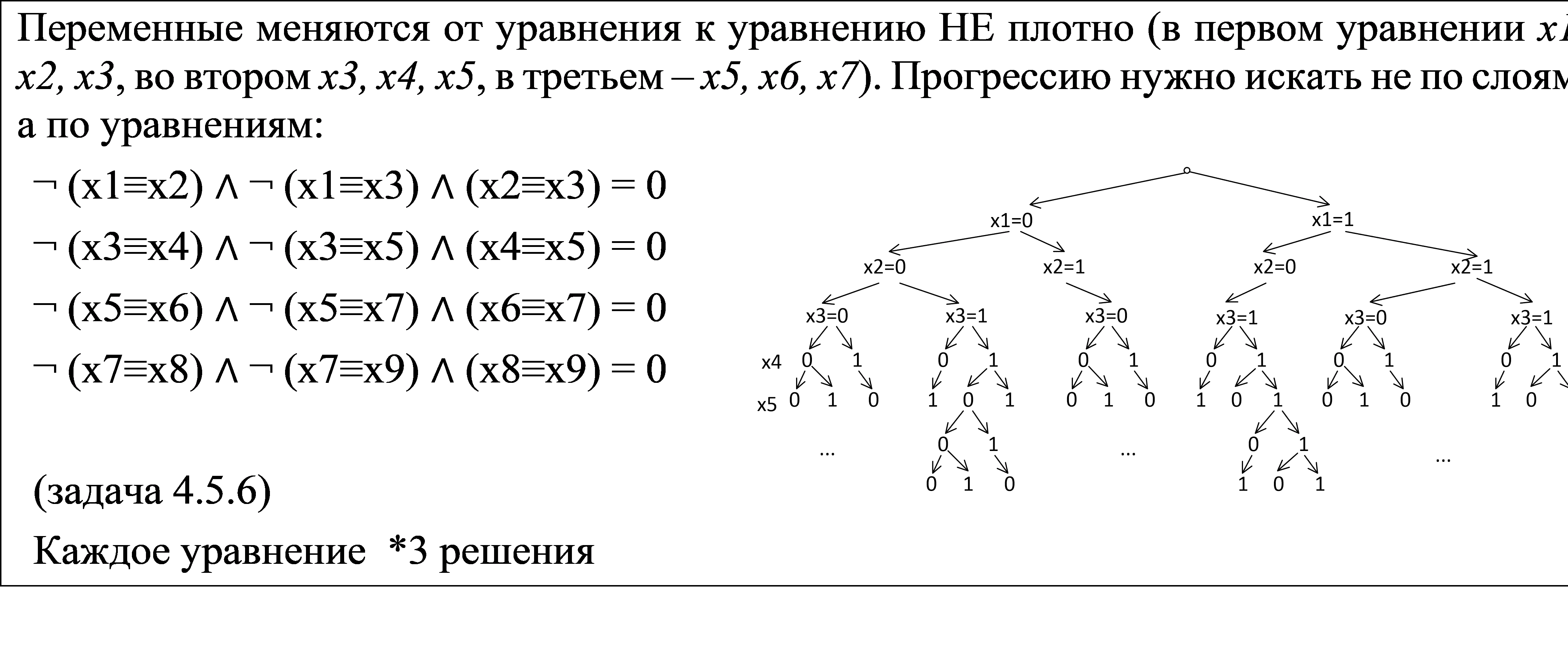

Задачи с несколькими наборами переменных
Сравните четыре прорешанных задачи и идеи их решений, чтобы «на глаз» определять путь, по которому решать подобные задачи:

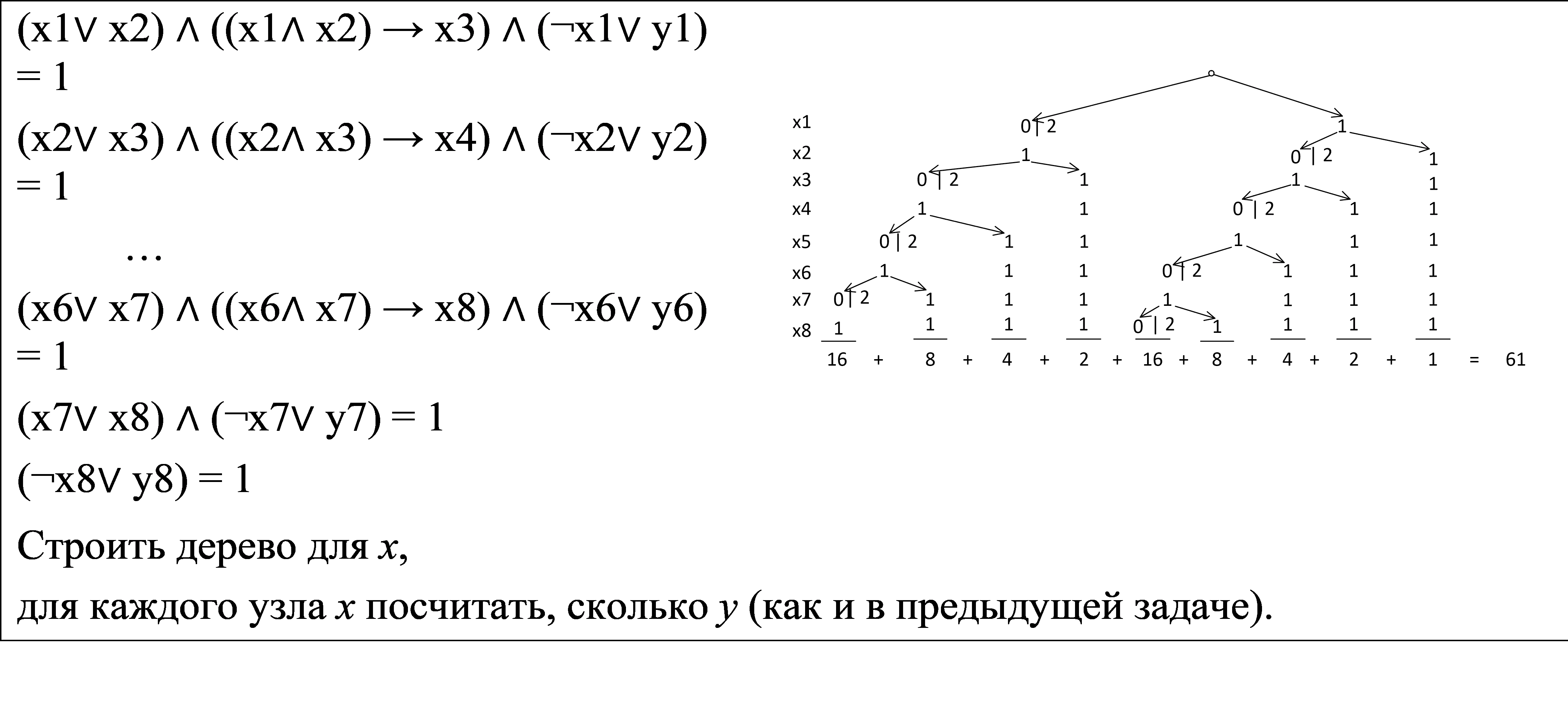
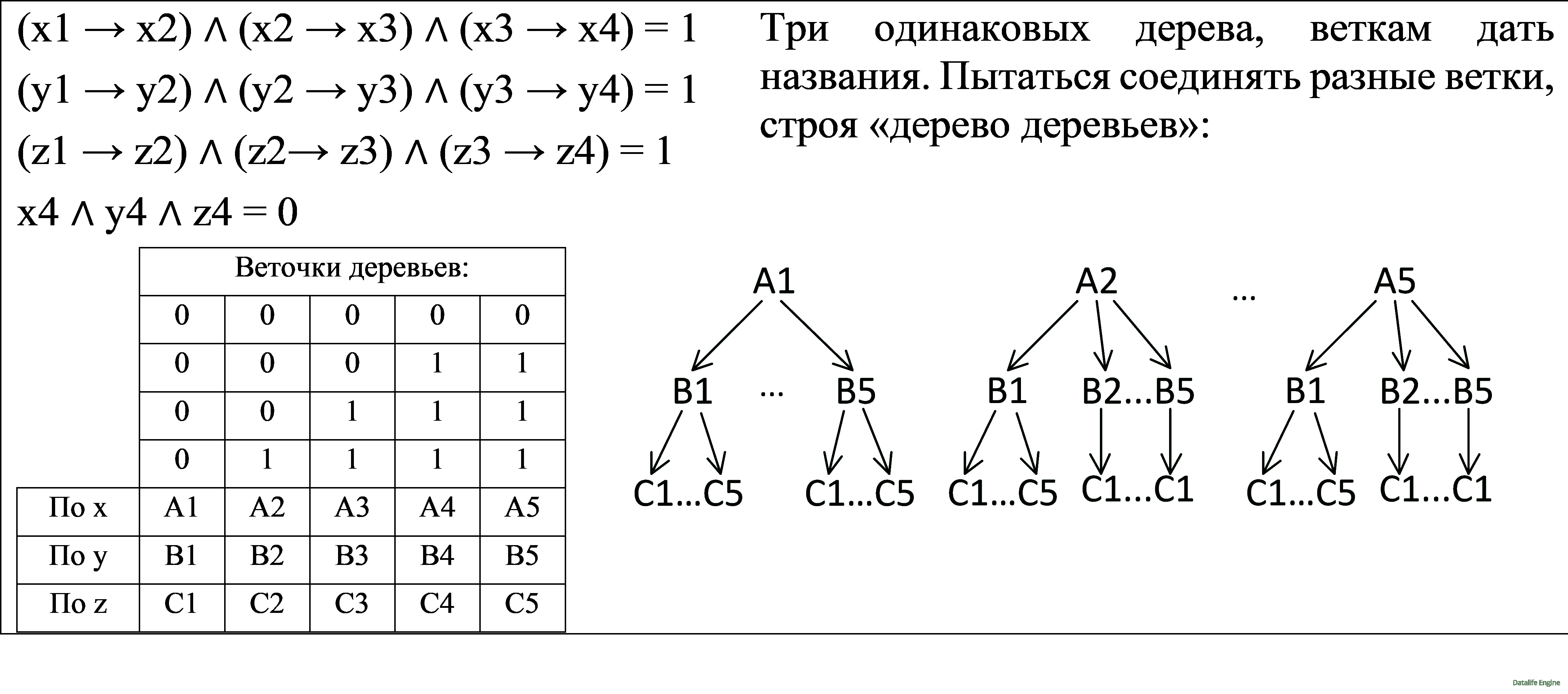
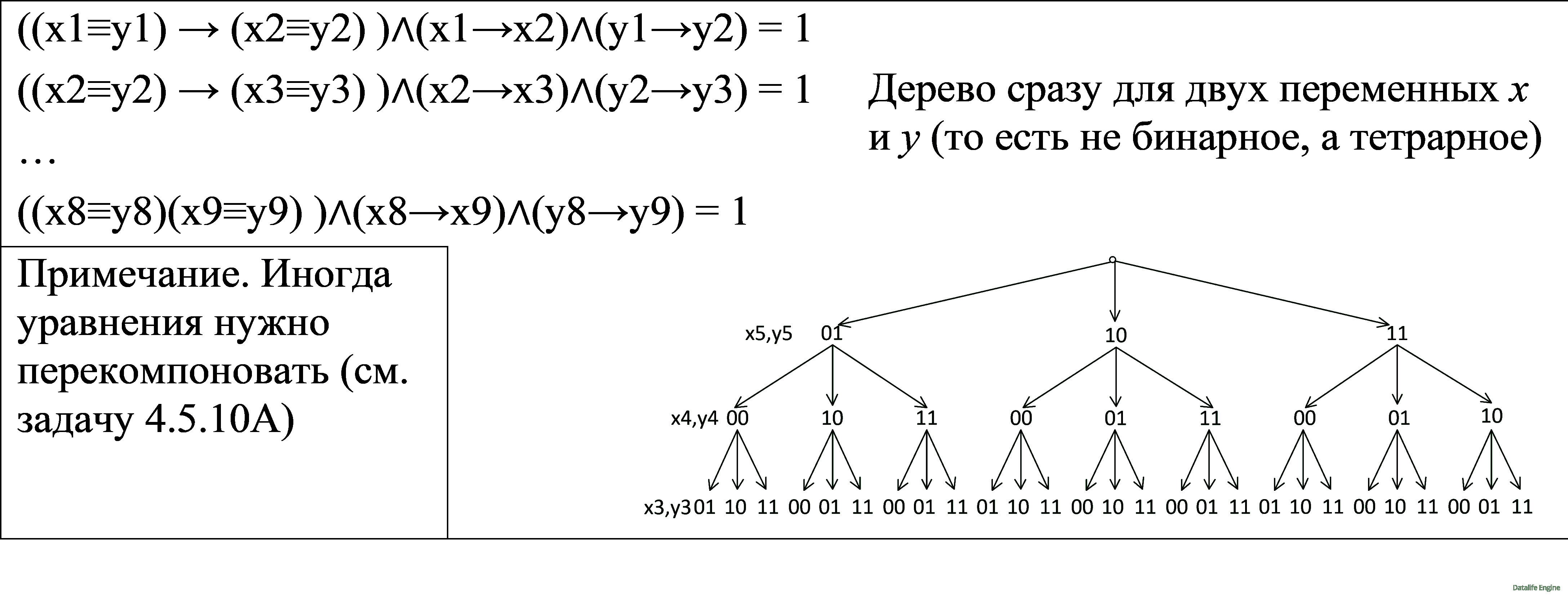
Разница между построением обычного дерева, введением новых обозначений и построением тетрарного дерева