Теперь нужно научиться переводить числа из одной системы счисления в другую.
Задача 1.3.1. Переведите число 1234-пятеричное в десятичную систему счисления.
Для начала распишем десятичное число 1234 в следующем виде:
1234 = 1000 + 200 + 30 + 4 = 1 * 103 + 2 * 102 + 3 * 101 + 4 * 100
Что мы сделали? Фактически, мы перевели десятичное число в его само!
А если у нас 12345? Вспомним, что все системы счисления устроены одинаково. Подумайте, что нужно поменять в приведенном выражении?
Распишем выражение точно также, как для 1234-десятеричного, заменив 10 на 5 и продолжим вычисления:
12345 = 1 * 53 + 2 * 52 + 3* 51 + 4 * 50 = 1 * 125 + 2 * 25 + 3 * 5 + 4 = 194
Но умножения и сложения мы выполняли в десятичной системе, следовательно, мы получили десятичное число 194, то есть перевели 12345 в десятичный вид. Такой перевод называется обратным.
Ответ: 194.
Задача 1.3.2. Переведите 165-десятичное в двоичную систему.
Попробуйте составить число 165 в виде суммы степеней двойки, как это было в обратном переводе.
Найдем для числа ближайшую степень двойки, не превосходящую 165, и вычтем её:
Продолжим вычитать степени двойки из остатка:
|
165
-128
|
= 128 + 32 +
|
|
37
-32
|
|
|
5
|
|
Будем вычитать степени двойки до тех пор, пока это возможно:
|
165
-128
|
= 128 + 32 + 4 + 1
|
|
37
-32
|
|
|
5
-4
|
|
|
1
|
|
Заполним полную таблицу степеней двоек:
|
степени 2
|
|
1
|
2
|
|
2
|
4
|
|
3
|
8
|
|
4
|
16
|
|
5
|
32
|
|
6
|
64
|
|
7
|
128
|
|
8
|
256
|
|
9
|
512
|
|
10
|
1024
|
|
11
|
2048
|
|
12
|
4096
|
Дополним ряд нашего числа недостающими степенями с коэффициентами 0:
|
165
-128
|
= 128 + 32 + 4 + 1
|
= 1*128 + 0*64 + 1*32 + 0*16 + 0*8 + 1*4 + 0*2 + 1*1
|
|
37
-32
|
|
|
|
5
-4
|
|
|
|
1
|
|
|
Если посмотреть эти равенства в обратном порядке, мы получим обратный перевод из двоичной системы в десятичную. Коэффициенты при степенях двойки и будут ответом – переводом числа в двоичный вид:
|
165
-128
|
= 128 + 32 + 4 + 1
|
= 1*128 + 0*64 + 1*32 + 0*16 + 0*8 + 1*4 + 0*2 + 1*1
1 0 1 0 0 1 0 1
|
|
37
-32
|
|
|
|
5
-4
|
|
16510 = 101001012
|
|
1
|
|
|
Ответ: 10100101
Задача 1.3.3. Переведите число 1711-десятичное в шестнадцатеричный вид.
Использовать метод из предыдущей задачи практически невозможно, так как нам придется не только составить список степеней основания 16, но и коэффициенты могут быть отличные от 0 - 1,2…15. На ЕГЭ сделать это нереально.
|
показатель коэф
степени
|
1
|
2
|
3
|
4
|
5
|
6
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
16
|
32
|
48
|
64
|
80
|
96
|
|
2
|
256
|
512
|
768
|
1024
|
1280
|
1536
|
|
3
|
4096
|
8192
|
12288
|
16384
|
20480
|
24576
|
|
4
|
65536
|
131072
|
196608
|
262144
|
327680
|
393216
|
|
5
|
1048576
|
2097152
|
3145728
|
4194304
|
5242880
|
6291456
|
|
6
|
16777216
|
33554432
|
50331648
|
67108864
|
83886080
|
100663296
|
Такой способ сгодится разве что для троичной системы счисления:
|
коэф
показатель степени
|
1
|
2
|
|
0
|
1
|
2
|
|
1
|
3
|
6
|
|
2
|
9
|
18
|
|
3
|
27
|
54
|
|
4
|
81
|
162
|
|
5
|
243
|
486
|
|
6
|
729
|
1458
|
|
7
|
2187
|
4374
|
Выбираем наиболее близкие числа из таблицы, составляем сумму, затем выписываем коэффициенты, не забывая про нули в том случае, если в сумме не присутствует степень ни в каком виде.
1711=1458+243+9+1
171110 = 21001013
Теория. Поскольку в 16-ричную систему так не перевести, придется запомнить универсальный способ перевода:
Прямой перевод (перевод из десятичной системы в n-ную) чуть сложнее. Для того, чтобы получить коэффициенты при степенях n, надо каскадно делить на n (сперва разделить исходное число на n, потом разделить получившийся результат на n … пока делится), потом записать число в виде остатков от деления в обратном порядке.
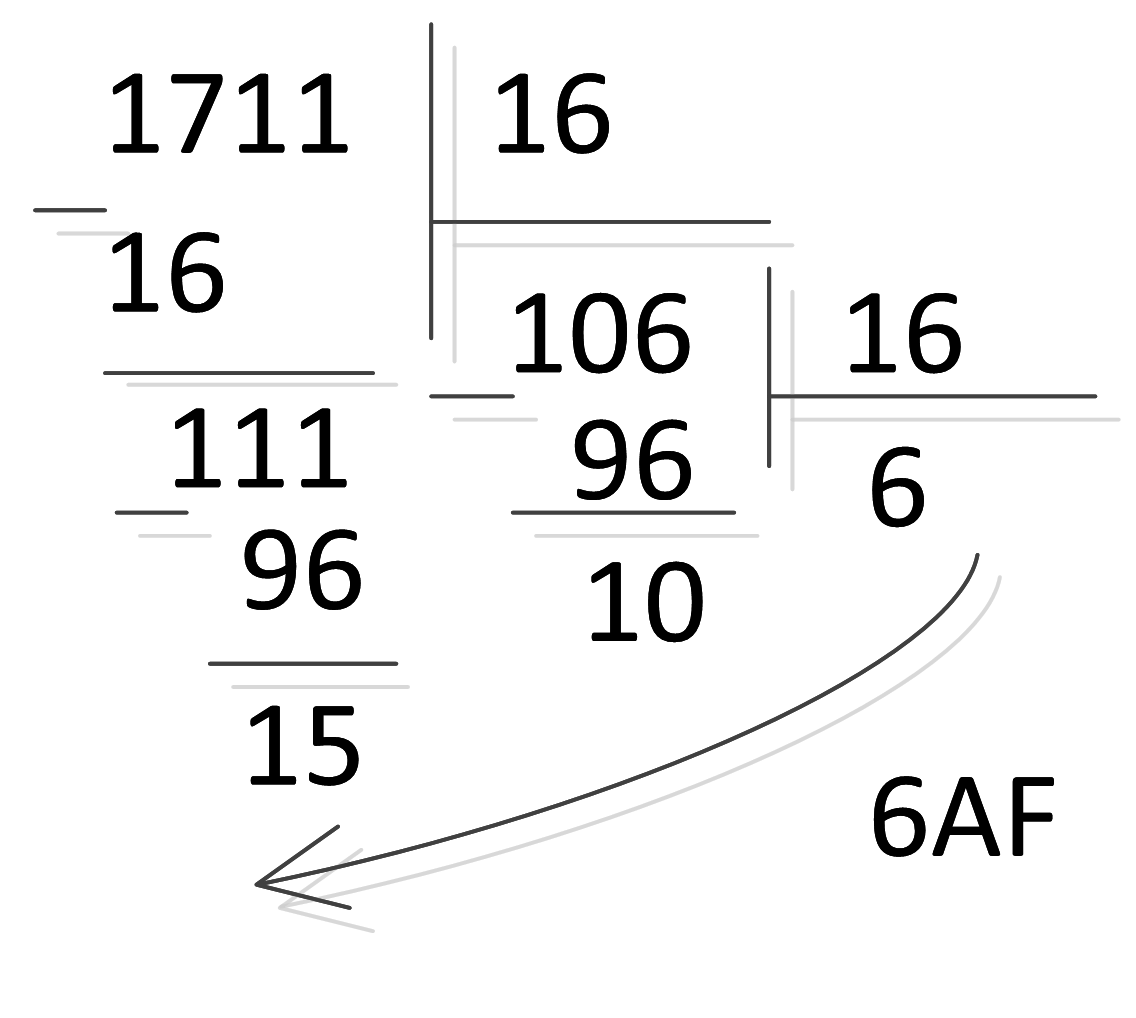
171110 = 6AF16
Ответ: 6АF
Вернемся к задаче 1.2.2. и переведем десятичное число в двоичную систему прямым переводом (каскадным делением).
Задача 1.3.4. Переведите 165-десятичное в двоичную систему прямым переводом.
|
165
|
2
|
|
|
|
|
|
|
|
1
|
82
|
2
|
|
|
|
|
|
|
|
0
|
41
|
2
|
|
|
|
|
|
|
|
1
|
20
|
2
|
|
|
|
|
|
|
|
0
|
10
|
2
|
|
|
|
|
|
|
|
0
|
5
|
2
|
|
|
|
|
|
|
|
1
|
2
|
2
|
|
|
|
|
|
|
|
0
|
1
|
Записываем остатки от деления в обратном порядке и получаем ответ.
Ответ: 10100101
Примечание. Может возникнуть вопрос, а для чего я вообще рассказал о переводе путем подбора степеней и коэффициентов, когда есть универсальный прямой перевод каскадным делением? Дело в том, что, по моему наблюдению, мои ученики путем подбора суммы степеней двоек делают меньше ошибок, чем при каскадном делении на 2. Я сам, когда переводил 165 каскадным делением на 2, сделал ошибку!
Задача 1.3.5. Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.
Нет необходимости переводить все числа в пятеричную систему. Достаточно это сделать для 10, и затем перечислить все числа до 17 в пятеричной системе.
|
10
|
5
|
|
-10
|
2
|
|
0
|
|
|
Десят.
|
Пятер.
|
|
10
|
20
|
|
11
|
21
|
|
12
|
22
|
|
13
|
23
|
|
14
|
24
|
|
15
|
30
|
|
16
|
31
|
|
17
|
32
|
Пересчитаем двойки, их окажется 7. Не пропустите случай с числом 12-десятичным, у которого двойки в обоих разрядах в пятеричной системе.
Задача 1.3.6. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 50, запись которых в системе счисления с основанием три оканчивается на 11.
Если выписывать все десятичные числа до 50 и рядом делать перевод, то это долго. Попробуйте сконструировать последовательность чисел, оканчивающихся в троичной системе на 11.
Прежде всего, это само число 11. Переведем его в десятичную обратным переводом:
113 = 1 * 3 + 1 = 410
Следующее за ним число:
1113 = 1 * 32 + 1 * 3 + 1 = 1310
Заметим, что последнюю сумму (выделена скобками):
1 * 32 + (1 * 3 + 1)
можно было бы и не делать, она у нас уже подсчитана:
1113 = 1 * 32 + 4 = 1310
Ошибка. Какое будет следующее число?
Если вы написали 1011, то вы ошиблись. Помните, что у нас троичная, а не двоичная система. Поэтому следующее число 211.
Продолжение хода решения:
2113 = 2 * 32 + 4 = 2210
А вот следующее число уже будет
10113 = 1 * 33 + 4 = 3110
Продолжим ряд чисел и заметим, что каждое следующее больше предыдущего на 9. Поэтому можно обойтись и без конструирования новых чисел в троичной системе:
Ответ: 4, 13, 22, 31, 40, 49
Примечание. Подход, когда задача решается для малых чисел, затем находится закономерность в последовательности чисел и прогрессия продолжается, довольно распространен в ЕГЭ. В приведенной задаче получается арифметическая прогрессия. Задача может быть усложнена увеличением количества членов прогрессии, когда надо будет найти сумму членов прогрессии. Формулы для суммы членов прогрессии надо знать или уметь вывести (они могут потребоваться и для других задач ЕГЭ).

