Теория. Очень часто в ЕГЭ бывает так, что перевести числа в альтернативные системы счисления можно быстрее, чем каскадным делением. Несколько приемов позволят вам сократить время на решение задачи. Дополним таблицу с системами счисления колонкой, в которой будут выделены степени некоторых чисел:
|
xn
|
десят
|
восьм
|
шест
|
двоич
|
троич
|
|
|
0
|
0
|
0
|
0
|
0
|
|
|
1
|
1
|
1
|
1
|
1
|
|
21
|
2
|
2
|
2
|
10
|
2
|
|
|
3
|
3
|
3
|
11
|
10
|
|
22 |
4
|
4
|
4
|
100
|
11
|
|
|
5
|
5
|
5
|
101
|
12
|
|
|
6
|
6
|
6
|
110
|
20
|
|
|
|
7
|
7
|
7
|
111
|
21
|
|
81
|
23
|
8
|
10
|
8
|
1000
|
22
|
|
32
|
9
|
11
|
9
|
1001
|
100
|
|
|
10
|
12
|
A
|
1010
|
101
|
|
|
11
|
13
|
B
|
1011
|
102
|
|
|
12
|
14
|
C
|
1100
|
110
|
|
|
13
|
15
|
D
|
1101
|
111
|
|
|
14
|
16
|
E
|
1110
|
112
|
|
|
|
15
|
17
|
F
|
1111
|
120
|
|
161
|
24
|
16
|
20
|
10
|
10000
|
121
|
|
|
17
|
21
|
11
|
10001
|
122
|
|
|
18
|
22
|
12
|
10010
|
200
|
|
|
19
|
23
|
13
|
10011
|
201
|
|
|
20
|
24
|
14
|
10100
|
202
|
|
|
21
|
25
|
15
|
10101
|
210
|
|
|
22
|
26
|
16
|
10110
|
211
|
|
|
23
|
27
|
17
|
10111
|
212
|
|
|
24
|
30
|
18
|
11000
|
220
|
|
52
|
25
|
31
|
19
|
11001
|
221
|
|
|
26
|
32
|
1A
|
11010
|
222
|
|
|
33
|
27
|
33
|
1B
|
11011
|
1000
|
Задача 1.2.1. Чему равно 128-десятичное в двоичной системе?
Не торопитесь каскадно делить 128 на 2. Обратите внимание, как в таблице выглядят числа-степени двойки в двоичной системе:
|
Показатель степени
|
Степень двойки в десятичной системе
|
Степень двойки в двоичной системе
|
|
0
|
1
|
1
|
|
1
|
2
|
10
|
|
2
|
4
|
100
|
|
3
|
8
|
1000
|
|
4
|
16
|
10000
|
Поскольку 128 – это 2 в седьмой степени, рискнем предположить, что
12810 = 100000002
То есть количество нулей равно показателю степени.
Ответ: 10000000.
Задача 1.2.2. Чему равно число 81-десятичное в троичной системе?
Решайте аналогично предыдущей задаче, но только для троичной системы счисления.
Рассмотрим степени числа 3 в троичной системе:
|
Показатель степени
|
Степень тройки в десятичной системе
|
Степень тройки в троичной системе
|
|
0
|
1
|
1
|
|
1
|
3
|
10
|
|
2
|
9
|
100
|
|
3
|
27
|
1000
|
То есть правило распространяется и на любую систему счисления (лишь бы основание системы счисления и основание степени совпадало):
8110 = 100003
Ответ: 10000
Задача 1.2.3. Чему равно 511-десятичное в двоичной системе счисления?
Обратите внимание на числа в таблице, которые меньше степеней двойки на 1.
Заметим, что 511=512-1. 512 – это 2 в девятой степени. Поэтому
51210 = 10000000002
Остается из этого числа вычесть 1. Но вычитать мы еще не научились. Если принять во внимание, что системы счисления устроены одинаково, то что будет, если мы из десятичного числа 1000 вычтем 1? Получим 999 - то есть последовательность из максимально возможных в системе счисления цифр. Аналогично рискнем предположить, что
51110 = 1111111112
И действительно, проверим по нашей таблице:
|
десят
|
двоич
|
|
1
|
1
|
|
2
|
10
|
|
3
|
11
|
|
4
|
100
|
|
7
|
111
|
|
8
|
1000
|
|
15
|
1111
|
|
16
|
10000
|
Ответ. 111111111.
Задача 1.2.4. Чему равно 80-десятичное в троичной системе?
Поступите, как в задачах «Чему равно 81-десятичное в троичной системе» и «Чему равно 511-десятичное в двоичной системе»
Закономерность из предыдущей задачи распространяется и на другие системы счисления.
80 = 81 – 1,8110 = 100003
Максимальная цифра в троичной системе – 2, поэтому:
8010 = 22223
Ответ: 2222.
Задача 1.2.5. Сколько цифр получится в числе при переводе 1050-десятичного в двоичную систему счисления?
Вам не обязательно переводить всё это число каскадным делением в двоичную систему – это медленно. Рассмотрите ближайшую к 1050 степень числа 2.
Ближайшая степень двойки к 1050 – число 1024. Поэтому
102410 = 10 000 000 0002 (1 и десять нулей)
Число 1050 будет отличаться от 1024 в двоичном виде несколькими единицами в некоторых разрядах. Но количество разрядов будет точно такое же – 11.
Ответ: 11.
Задача 1.2.6. Десятичное число кратно 16. Какое минимальное количество нулей будет в конце этого числа после перевода его в двоичную систему счисления?
Рассмотрите начало ряда чисел, которые делятся на 16, переведите их в двоичную систему.
Минимальное число, кратное 16 – это само число 16. Оно равно 2 в 4 степени, поэтому:
1610 = 100002
Есть ли гарантия, что числа, кратные 16, также оканчиваются как минимум на 4 нуля?
Следующее число, кратное 16 – 32, является 2 в степени 5, следовательно
3210 = 1000002
Затем идет число 48=32+16, следовательно
4810 = 1100002
Ответ: 4.
Задача 1.2.7. Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Рассмотрите в таблице с числами в разных системах счисления числа, кратные основанию систем счисления, например, четные числа в двоичной системе.
Если мы рассмотрим таблицу с переводом чисел в разные системы счисления, мы увидим, что в двоичной системе четные числа оканчиваются на 0, в троичной системе числа, делящиеся на 3, оканчиваются на 0. Правило распространяется и на любую систему счисления. Если некоторое число в троичной системе оканчивается на 0, то оно делится на 3, а если в пятеричной, то оно делится на 5. Значит, наше число делится на 3 и на 5 одновременно. Такое минимальное число равно 15.
Ответ: 15
Задача 1.2.8. Запись десятичного числа в системах счисления с основаниями 10 и 12 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Это задача является усложненной версией предыдущей.
Ошибка. Если вы ответили 10*12=120, то вы ошиблись, потому что есть число 60, которое делится на 12 и на 10.
Правильный алгоритм решения заключается в поиске наименьшего общего кратного (НОК) оснований систем:
10=2*5
12=2*2*3
Алгоритм поиска заключается в том, что мы разлагаем основания систем на простые множители и в НОК выписываем эти множители только один раз:
|
10=
|
2*
|
|
|
5
|
|
|
12=
|
2*
|
2*
|
3
|
|
|
|
НОК=
|
2*
|
2*
|
3*
|
5
|
=60
|
Ответ: 60
Примечание. Запомните этот алгоритм, он пригодится и при решении других задач ЕГЭ!
Задача 1.2.9. Значение арифметического выражения: 98 + 38 – 2 – записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Вспомните, как выглядят степени числа в системах счисления таких же, как и основание степени.
Медленный путь заключается в том, чтобы посчитать значение выражения в десятичной системе, а затем каскадным делением перевести в троичную. Но есть и способ быстрее. Обратим внимание, что:
98 + 38 – 2 =316 + 38 – 2.
Степени тройки в троичной системе представляют собой 1 и 0 в количестве, равном показателю степени:
31610 = 10000 0000 0000 00003
3810 = 10000 00003
Сложим столбиком:
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
+
|
|
|
|
|
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Остается вычесть 2. Сделаем это в два этапа: сперва вычтем 1. Мы уже знаем, что при вычитании 1 из числа со многими нулями мы получим последовательность максимальных цифр:
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
+
|
|
|
|
|
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
И еще раз вычтем 1:
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
+
|
|
|
|
|
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
|
-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
То есть в числе 7 двоек.
Ответ: 7
Задача 1.2.10. Сколько единиц содержится в двоичной записи значения выражения:
42014 + 22015 – 8
Эта задача решается аналогично предыдущей. Надо лишь придумать, как записывать большие числа с повторяющимися нулями.
42014 + 22015 – 8 = 24028 + 22015 – 23
Затруднение может вызвать изображение этого числа в двоичном виде. Запишем сложение чисел со значком «и так далее» и подсчетом количества нулей и единиц.
|
|
4028-2015-1=
2012 нулей
|
|
2015-3=2012
нулей
|
|
|
|
|
1
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
|
|
|
|
+
|
1
|
0
|
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
-
|
1
|
0
|
0
|
0
|
|
1
|
0
|
…
|
0
|
1
|
0
|
…
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
-
|
1
|
0
|
0
|
0
|
|
1
|
0
|
…
|
0
|
0
|
1
|
…
|
1
|
0
|
0
|
0
|
Итак, всего 2013 единиц (не забудьте про первую единицу).
Ответ: 2013
Задача 1.2.11. Сколько единиц содержится в двоичной записи значения выражения:
4511 + 2511 – 511
Вычитать число с большим количеством единиц (то есть 511) очень тяжело. Попробуйте его заменить на выражение из степеней двоек.
Преобразуем исходное выражение так, чтобы оно представляло собой выражение из степеней двойки:
4511 + 2511 – 511 = 21022 + 2511 – 29 + 1
Аналогично предыдущей задаче, выполним арифметические операции:
|
|
1022-511-1=
510 нулей
|
|
511-9=502
нуля
|
|
|
|
|
|
|
|
|
|
|
1
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
+
|
1
|
0
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
-
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+
|
1
|
|
1
|
0
|
…
|
0
|
1
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
|
|
|
|
|
|
-
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
…
|
0
|
0
|
1
|
…
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
Всего единиц: 1+502+1=504.
Ответ: 504
Задача 1.2.12. Сколько единиц содержится в двоичной записи значения выражения:
(64132 + 1618 + 1)*824 + 42 – 1
Представьте выражение в виде суммы степеней двойки - 1.
(64132 + 1618 + 1) * 824 + 42 – 1 =
(26* 132 + 24*18 +1) * 23*24 + 22*2 – 1 =
26*132 * 23*24 + 24*18 * 23*24 + 1 * 23*24 + 22*2 – 1 =
26*132+3*24 + 24*18+3*24 + 23*24 + 22*2 – 1 =
2864 + 2144 + 272 + 24 – 1
Аналогично предыдущим задачам, первым трем слагаемым соответствуют числа с единицей и нулями в количестве показателя степени. То есть, суммируя первые три слагаемых, мы получим число с тремя единицами.
Определим, сколько единиц в числе 24 – 1:
3+4=7.
Ответ: 7.
Задача 1.2.13. Сколько единиц содержится в двоичной записи значения выражения: 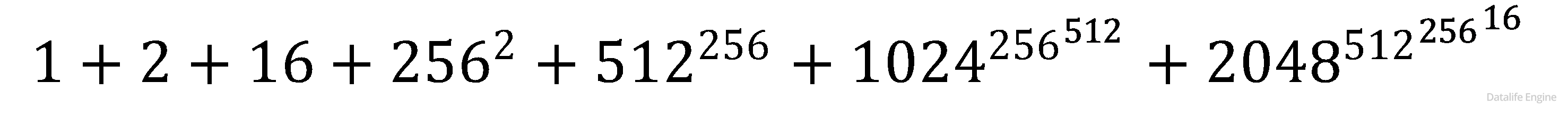
Решайте, как в предыдущих задачах. При этом подсчитывать количество нулей не обязательно.
Каждое слагаемое представляет собой степень двойки, следовательно, в двоичном виде оно является 1 с вереницей нулей. Каждое следующее слагаемое содержит всё большее количество нулей:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+
|
1
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+
|
1
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
+
|
1
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
+
|
1
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
+
|
1
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
…
|
0
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
…
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
…
|
1
|
0
|
…
|
0
|
1
|
0
|
…
|
0
|
1
|
0
|
…
|
0
|
1
|
0
|
0
|
1
|
1
|
Таким образом, количество единиц в сумме равно количеству слагаемых, то есть 7.
Ответ: 7.