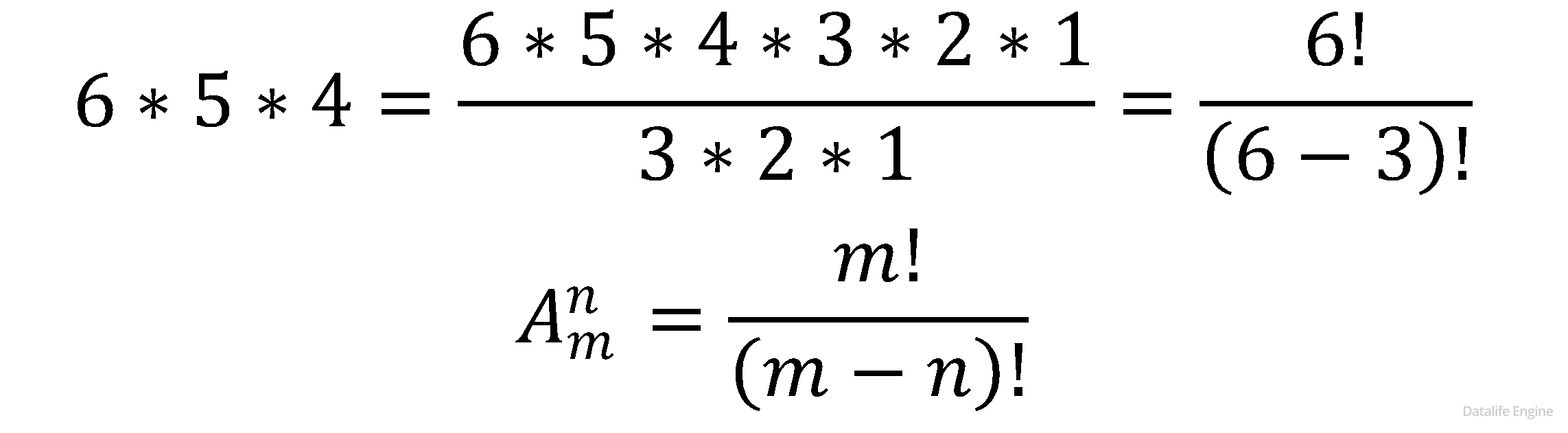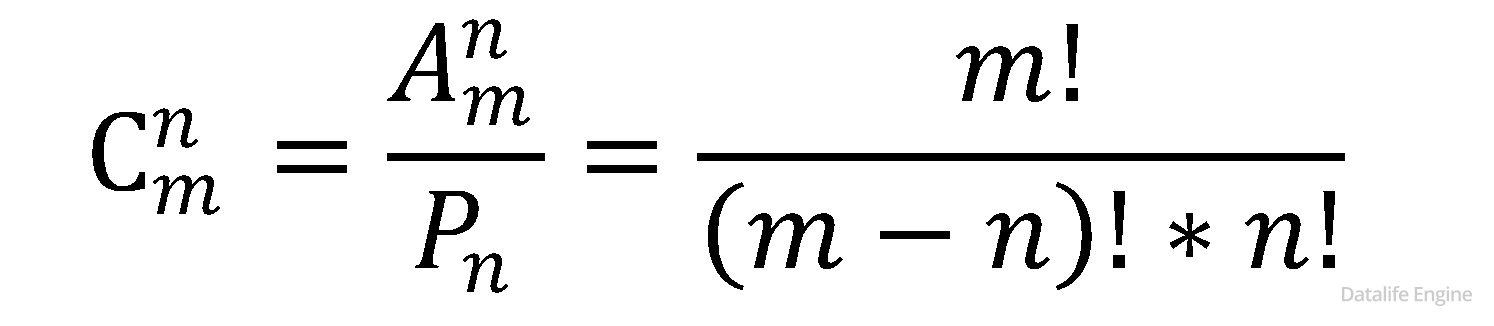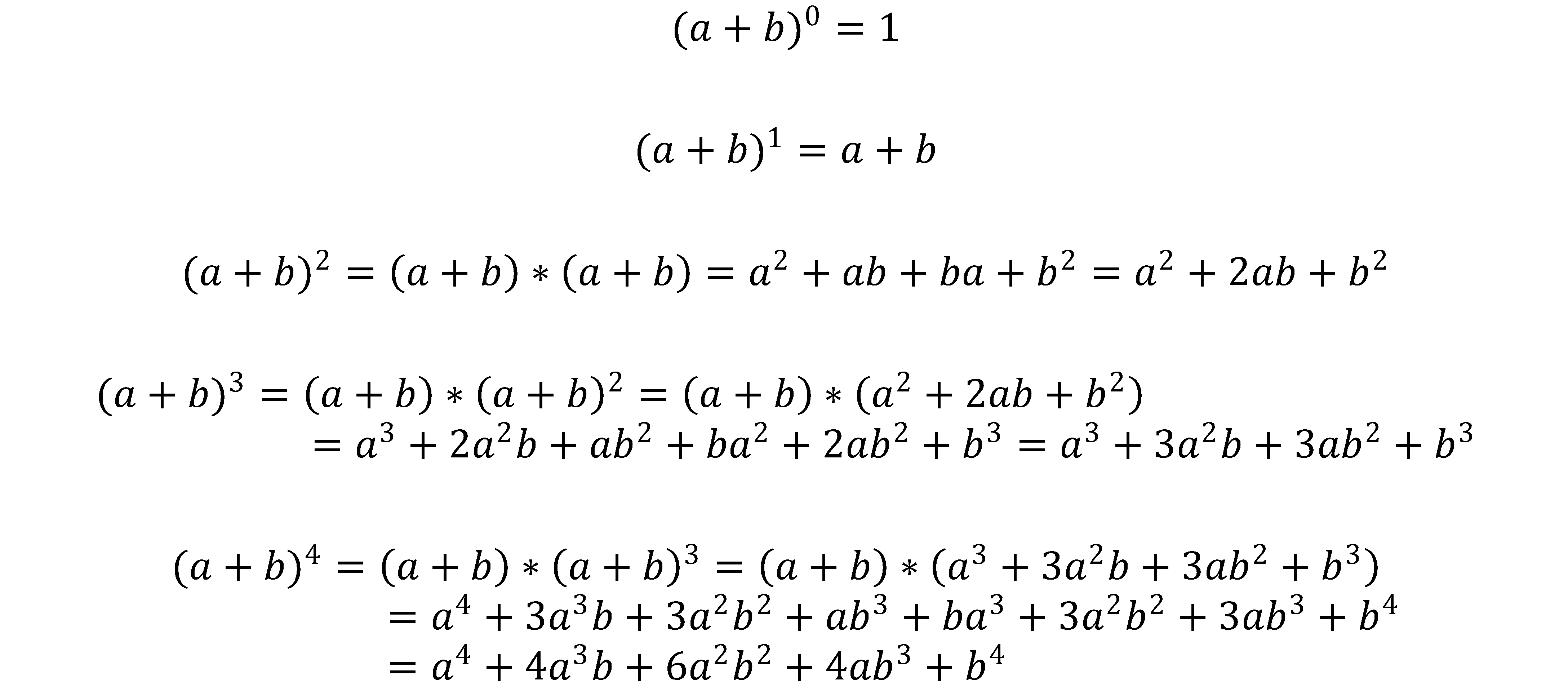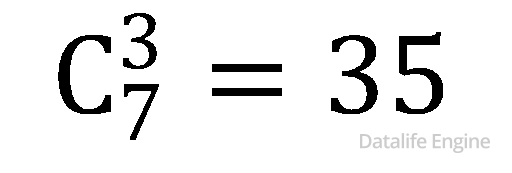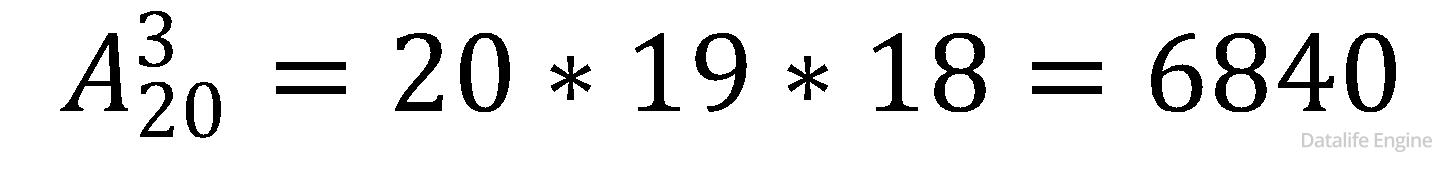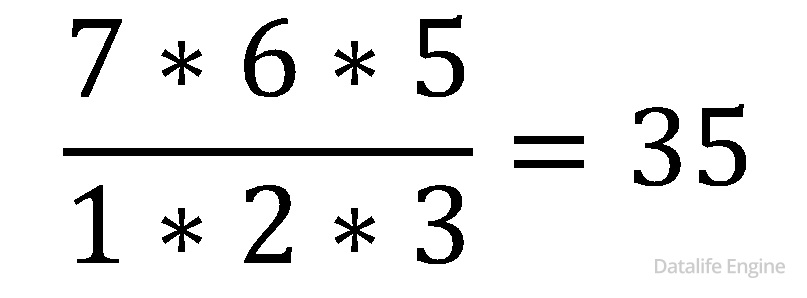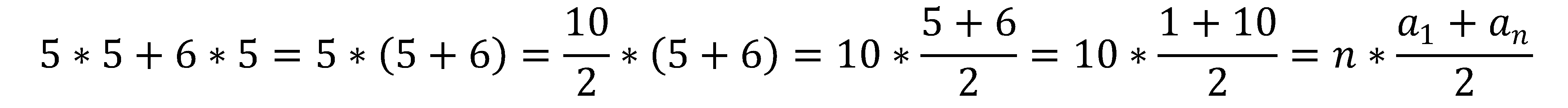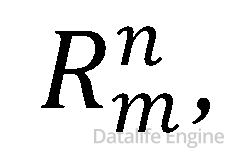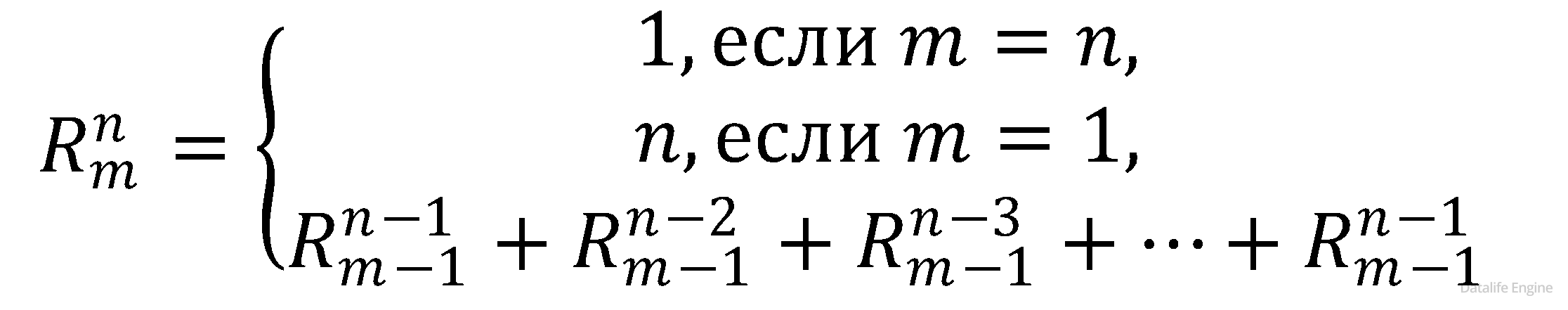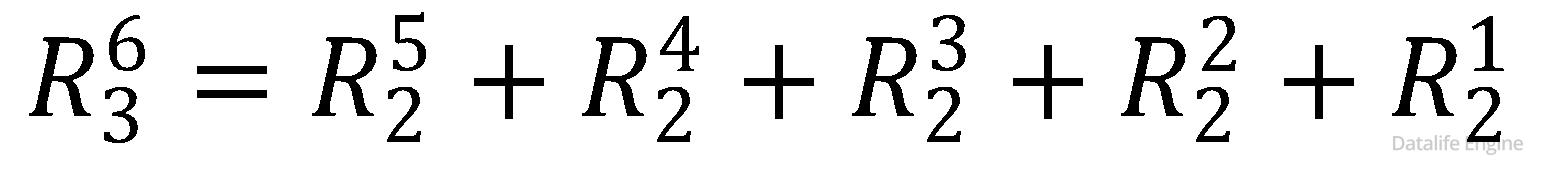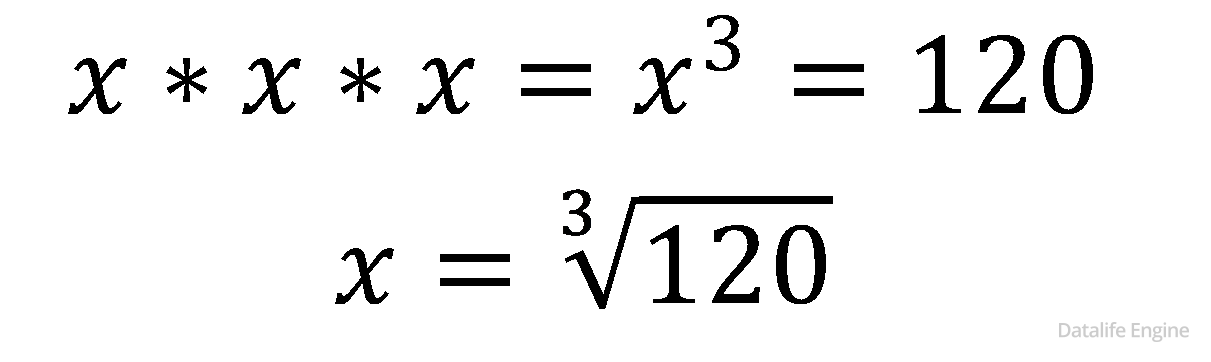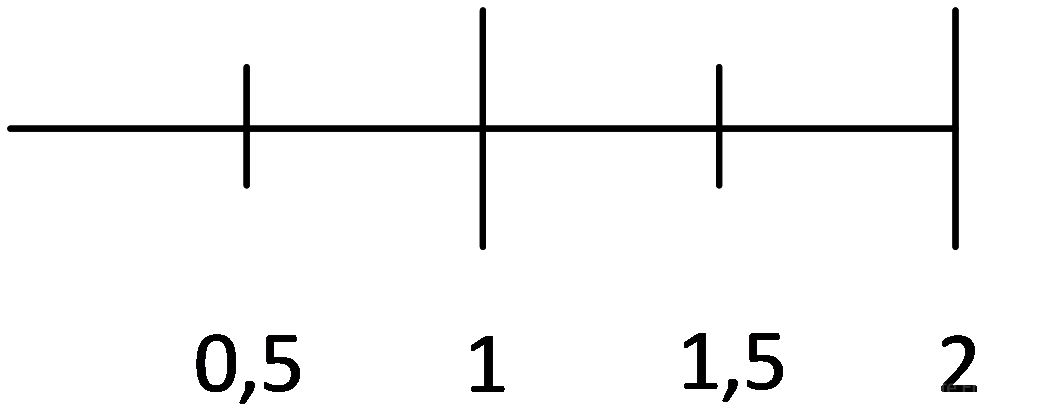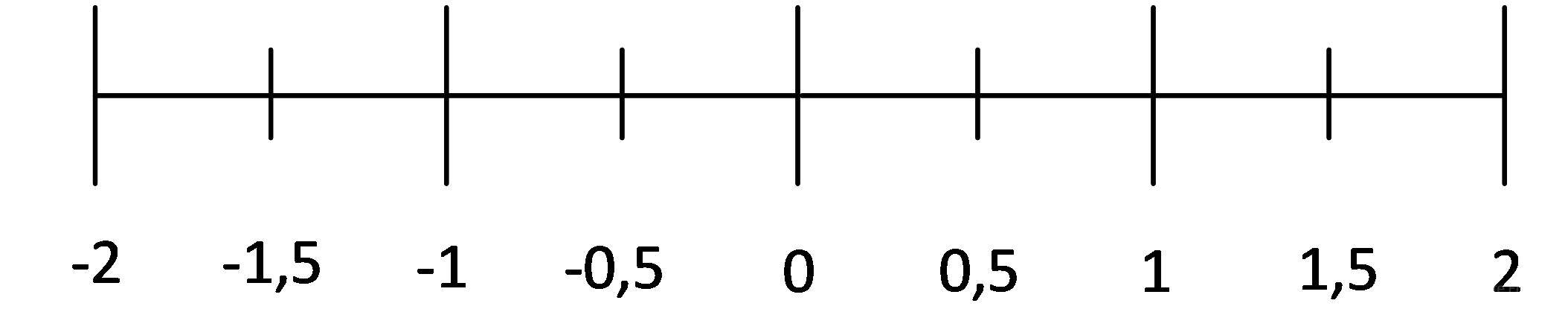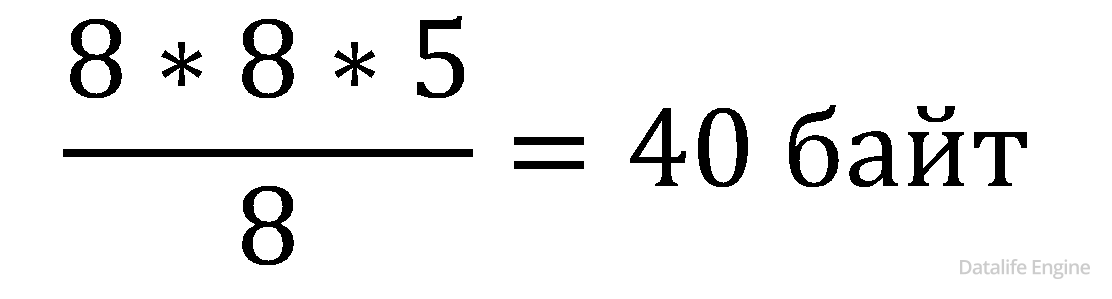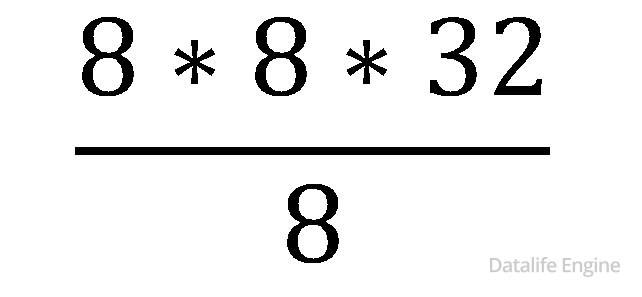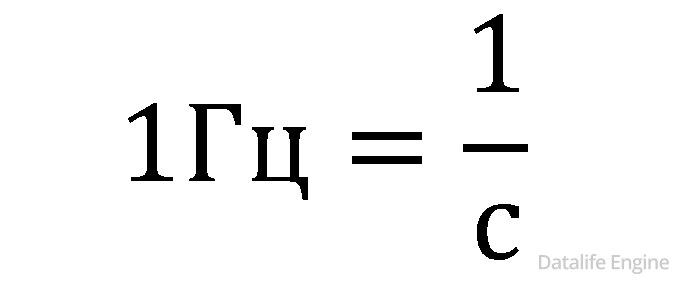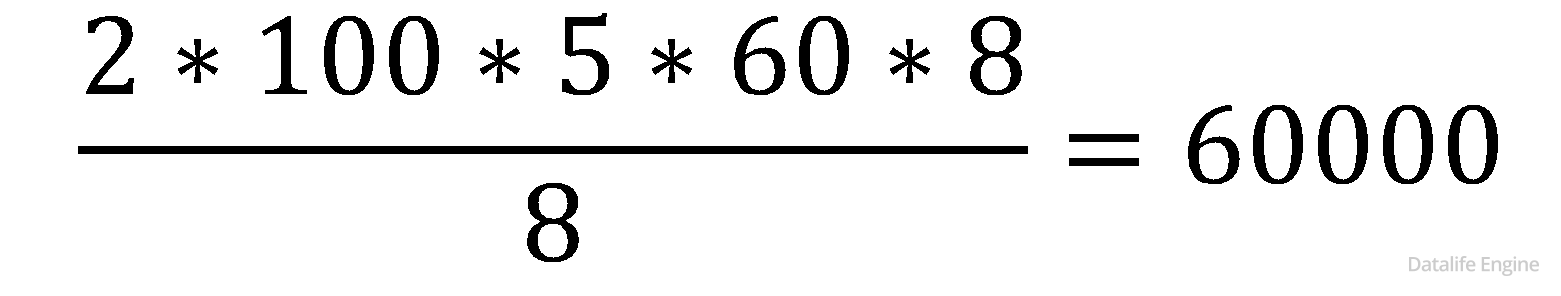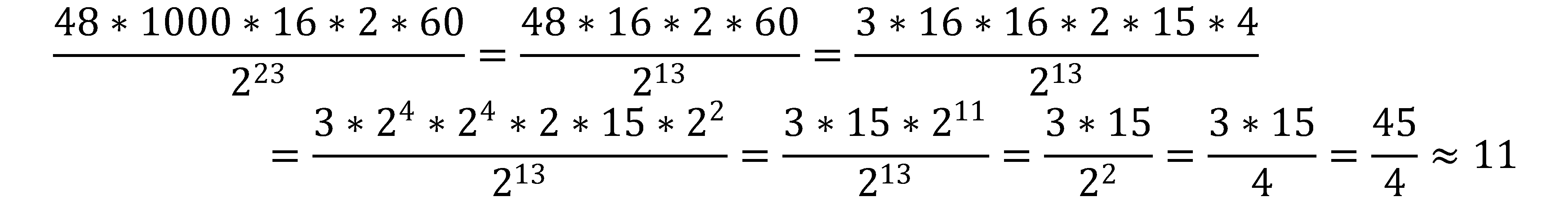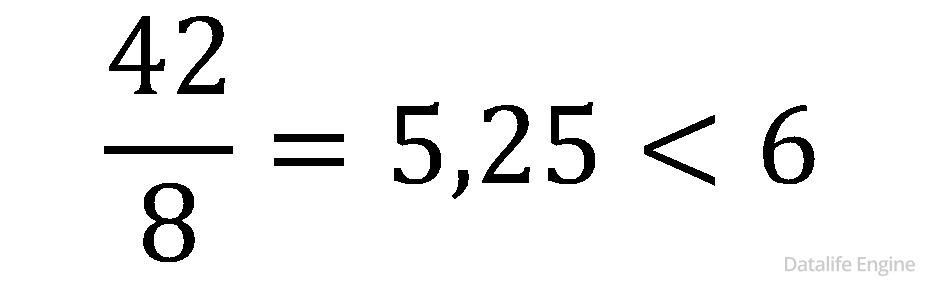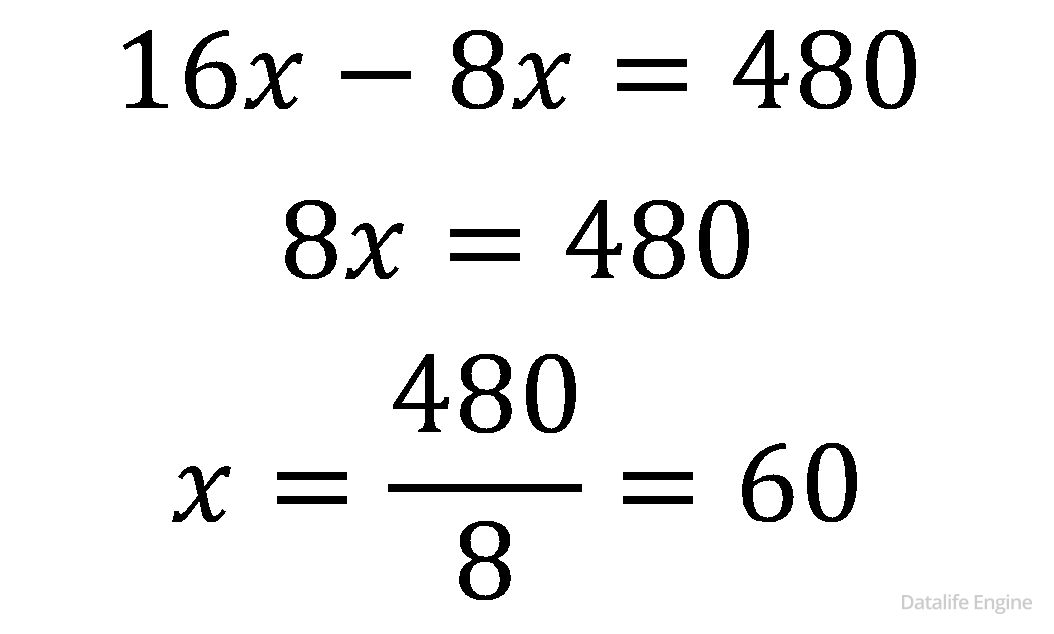Это один из важнейших параграфов. Подходы к решению задач, изложенные здесь, используются почти во всех других главах книги. Важно не только выучить, но и понять весь изложенный здесь материал. На основе теории из этого параграфа построена целая глава этой книги «Комбинаторика» (предпоследняя).
Задача 2.2.1. Сколько можно составить пятибуквенных слов, если используются только буквы A, B, C (каждая буква может повторяться несколько раз или не встречаться в слове вовсе).
Подумайте сперва, сколько можно составить слов из одной буквы, затем из двух, трех и т.д. При этом записывайте слова в алфавитном порядке (или как числа в системах счисления – по возрастанию).
Если у нас слово состоит только из одной буквы, то мы можем составить следующие слова:
Если мы добавим вторую ячейку, то получим уже 9 слов. Чтобы соблюдать алфавитный порядок, запишем уже имеющиеся однобуквенные слова с буквой А, потом их же с буквой B, потом их же с буквой C.
|
|
|
|
A
|
A
|
|
А
|
B
|
|
А
|
C
|
|
B
|
A
|
|
B
|
B
|
|
B
|
C
|
|
C
|
A
|
|
C
|
B
|
|
C
|
C
|
Добавим третью ячейку. Для соблюдения алфавитного порядка повторим список двухбуквенных слов три раза: первый раз с добавленной буквой А, второй раз – с буквой B, третий раз – с буквой C. Таким образом, мы получим 27 слов:
|
|
|
|
|
А
|
A
|
A
|
|
А
|
А
|
B
|
|
А
|
А
|
C
|
|
А
|
B
|
A
|
|
А
|
B
|
B
|
|
А
|
B
|
C
|
|
А
|
C
|
A
|
|
А
|
C
|
B
|
|
А
|
C
|
C
|
|
B
|
A
|
A
|
|
B
|
А
|
B
|
|
B
|
А
|
C
|
|
B
|
B
|
A
|
|
B
|
B
|
B
|
|
B
|
B
|
C
|
|
B
|
C
|
A
|
|
B
|
C
|
B
|
|
B
|
C
|
C
|
|
C
|
A
|
A
|
|
C
|
А
|
B
|
|
C
|
А
|
C
|
|
C
|
B
|
A
|
|
C
|
B
|
B
|
|
C
|
B
|
C
|
|
C
|
C
|
A
|
|
C
|
C
|
B
|
|
C
|
C
|
C
|
Таким образом, добавление каждой дополнительной ячейки приведет к утроению имеющегося списка слов. Поскольку у нас 5 ячеек, то 3 * 3 * 3 * 3 * 3 = 243.
Ответ. 243.
Теория. Целесообразно вывести формулу. Количество букв (ячеек) в слове (в нашей задаче - 5) –это показатель степени, в которое мы возвели число 3. А откуда взялось число 3 – основание степени? Это мощность алфавита, то есть количество букв, которые могут использоваться при составлении слов (в нашей задаче – А, В, C). Таким образом, получаем формулу:
w = mn
Где w-количество слов, m-мощность алфавита, n-количество ячеек.
Примечание 1. Некоторые ученики предпочитают выучить формулу, но очень часто при решении задачи путают основание и показатель степени, то есть наоборот, количество ячеек возводят в степень мощности алфавита. Кроме того, задача может быть сформулирована и так: «Первая ячейка принимает значения из 2 букв, вторая из четырех, третья – из шести». В этом случае количество слов вычисляется через произведение 2 * 4 * 6. И вы об этом легко догадаетесь, если запомните ход решения, но формула вам для получения решения никак не поможет. Это пример того, почему важно понять и запомнить ход рассуждений, а не формулу.
Примечание 2. Есть связь с системами счисления. Если в нашей задаче мы заменим буквы на цифры, то получим последовательность чисел в троичной системе. Последнее число будет 222-троичное. Но поскольку ряд чисел начинается с нуля, то всего будет чисел 1000 (но это ответ в троичном виде). Переведем его в десятичный вид, чтобы получить ответ в десятичном виде:
100003 = 1 * 35 = 24310
Задача 2.2.2. Есть четыре флага разных цветов и четыре мачты. Сколько можно передать сообщений, если флаги вывешивать на мачты в разном порядке (на каждой мачте обязательно должен висеть один из флагов).
Подход к решению задачи точно такой же, как и к предыдущей, но есть различие: флагов у нас ограниченное количество - по одному флагу каждого цвета (в предыдущей задаче каждого вида буква была в неограниченном количестве), следовательно, формула в этой задаче должна отличаться от предыдущей.
Ход решения:
|
Обозначим цвета флагов цифрами: 0,1,2,3
Если бы у нас была только одна мачта, мы могли бы вывесить на неё один из четырех флагов, то есть смогли бы передать четыре различных сообщения:
|
|
Добавим вторую мачту:
|
Мачта №1
|
Мачта №2
|
|
0
|
1
|
|
2
|
|
3
|
|
1
|
0
|
|
2
|
|
3
|
|
2
|
0
|
|
1
|
|
3
|
|
3
|
0
|
|
1
|
|
2
|
|
Поскольку мы на одну мачту один флаг уже вывесили, то у нас остается выбор не из четырех флагов, а из трех. В этом заключается отличие от предыдущей задачи. Там мы бы умножили 4 * 4, а в этой задаче при добавлении второй мачты мы получим 4*3=12 сообщений.
Добавим третью мачту:
|
Мачта №1
|
Мачта №2
|
Мачта №3
|
|
0
|
1
|
2
|
|
3
|
|
2
|
1
|
|
3
|
|
3
|
1
|
|
2
|
|
1
|
0
|
2
|
|
3
|
|
2
|
0
|
|
3
|
|
3
|
0
|
|
2
|
|
2
|
0
|
1
|
|
3
|
|
1
|
0
|
|
3
|
|
3
|
0
|
|
1
|
|
3
|
0
|
1
|
|
2
|
|
1
|
0
|
|
2
|
|
2
|
0
|
|
1
|
Поскольку на двух мачтах у нас уже висят два флага, то у нас остается выбор только из двух флагов, которые мы повесим на третью мачту, следовательно, количество сообщений, которые мы можем передать, равно 4 * 3 * 2 = 24.
Добавим четвертую мачту:
|
Мачта №1
|
Мачта №2
|
Мачта №3
|
Мачта №4
|
|
0
|
1
|
2
|
3
|
|
3
|
2
|
|
2
|
1
|
3
|
|
3
|
1
|
|
3
|
1
|
2
|
|
2
|
1
|
|
1
|
0
|
2
|
3
|
|
3
|
2
|
|
2
|
0
|
3
|
|
3
|
0
|
|
3
|
0
|
2
|
|
2
|
0
|
|
2
|
0
|
1
|
3
|
|
3
|
1
|
|
1
|
0
|
3
|
|
3
|
0
|
|
3
|
0
|
1
|
|
1
|
0
|
|
3
|
0
|
1
|
2
|
|
2
|
1
|
|
1
|
0
|
2
|
|
2
|
0
|
|
2
|
0
|
1
|
|
1
|
0
|
Добавление флага на четвертую мачту никак не повлияло на количество сообщений, так как на четвертую мачту мы можем вывесить только один оставшийся флаг. Количество сообщений равно 4 * 3 * 2 * 1 = 24.
Ответ: 24.
Теория. Решеная задача называется перестановками, выражение вида 1 * 2 * 3 * 4 – факториалом. Формула для вычисления:
Pn = n! = 1 * 2 * 3 * … * n
Задача могла бы быть сформулирована в более общем виде, например, есть 6 флагов и три мачты. Тогда произведение не нужно было бы доводить до конца: 6*5*4.
Выведем формулу через факториалы для нашего примера:
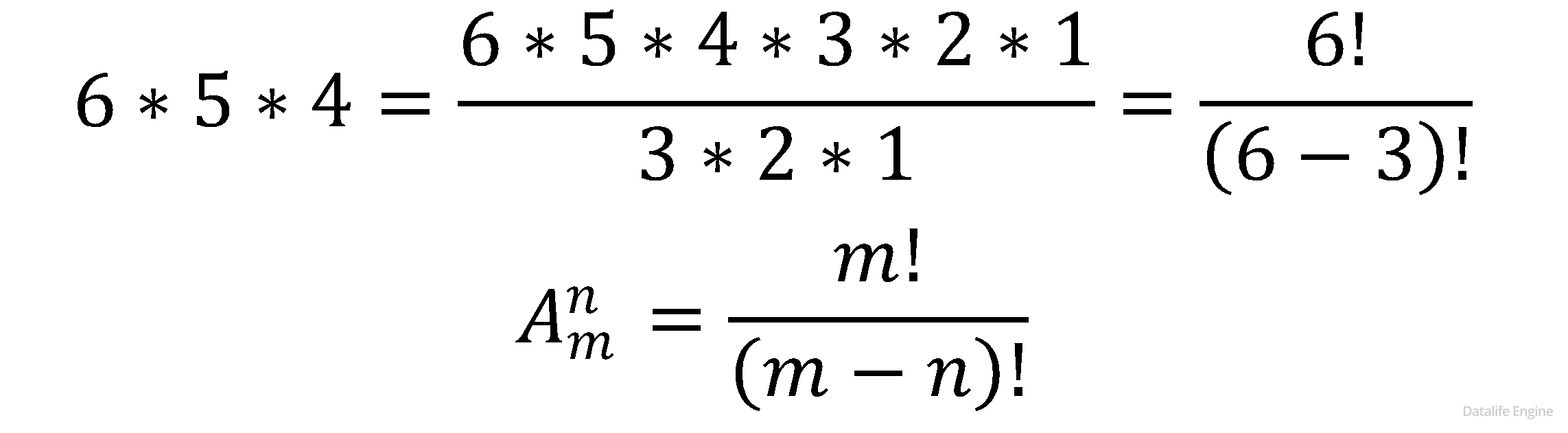
Эта задача называется размещением и обозначается буквой A, от английского и французского arrangement. В формуле m – это мощность алфавита (количество разных предметов, которые существуют только в одном экземпляре), а n-количество ячеек.
Примечание. На ЕГЭ формулу можно не вспомнить, поэтому будет лучше, если вы поймете и запомните ход рассуждений. Подвохом может быть то, что в задаче будет большое количество предметов и ячеек. Поэтому важно уметь привести пример на маленьких числах и понять принцип вычислений.
Задача 2.2.3. В магазине продается 7 видов фруктов. Мы можем купить только три вида фруктов, чтобы сделать из них салат. Сколько различных видов салатов мы могли бы приготовить из имеющегося в магазине ассортимента?
Начните считать, как в задаче на размещения, а потом подумайте, как можно сократить количество решений задачи, причем тоже с помощью размещений.
Решим сперва задачу на размещения:

Проблема в том, что это задача – не на размещения. Отличие от предыдущей задачи следующее. Когда мы вывешивали флаги на мачты, то имел значение порядок мачт. То есть:
Мачта 1 – синий флаг,
Мачта 2 – красный флаг,
Мачта 3 – желтый флаг.
Это одно сообщение, а:
Мачта 1 – красный флаг,
Мачта 2 – синий флаг,
Мачта 3 – желтый флаг.
Это уже другое сообщение.
В нашем случае мы бы решали такую же задачу, если бы фрукты выкладывали в разные тарелки, но мы-то делаем салат – кладем их в одну тарелку. Таким образом, количество решений должно быть меньшим.
Поскольку у нас в салате три компонента, то шесть найденных нами решений с помощью расстановок будут одинаковыми:
xyz
xzy
yxz
zxy
yzx
zxy
А как определить, что их 6? Это та же задача, что и на перестановки (когда было 4 флага и мы их вывешивали на 4 мачты). То есть в нашем случае:
P3 = 3! = 1 * 2 * 3
В задаче на фрукты вместо x, y, z мы можем поставить любые три фрукта. Таким образом, посчитанное количество размещений нам нужно сократить в 6 раз.
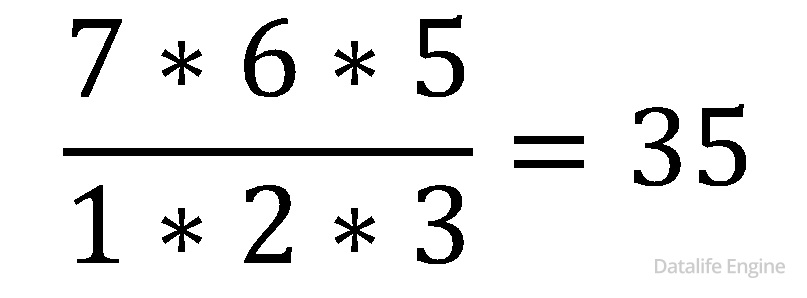
Ответ: 35.
Теория 1. Рассмотренная задача с салатом называется задачей на сочетания и обозначается буквой С (от латинского combinatio). Она тесно связана с расстановками и перемещениями формулой:
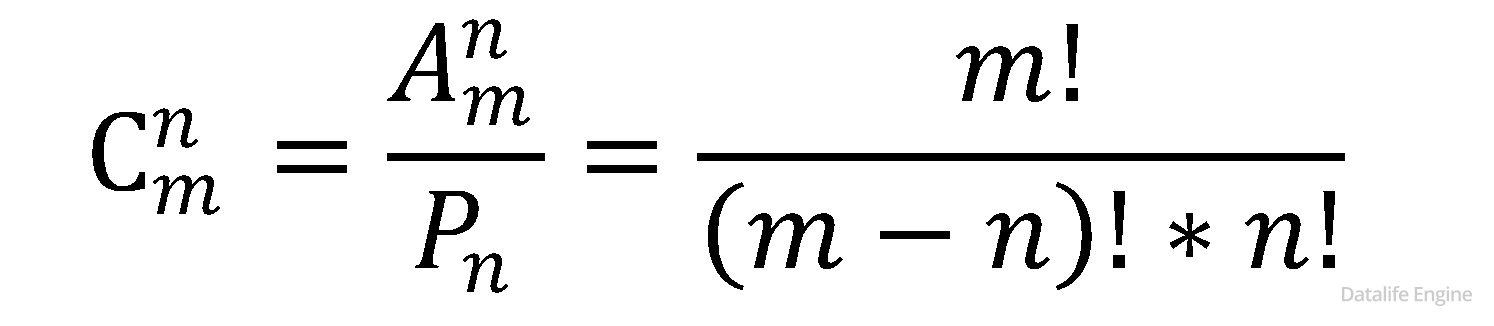
Я не советую запоминать формулу, так как очень легко ошибиться. Намного проще понять и запомнить ход решения, тогда вероятность ошибки снизится.
Теория 2. С комбинаторикой тесно связан бином Ньютона и треугольник Паскаля. Эта информация является дополнительной, поэтому, если вы ограничены во времени, можете её не читать.
Рассмотрим формулы:
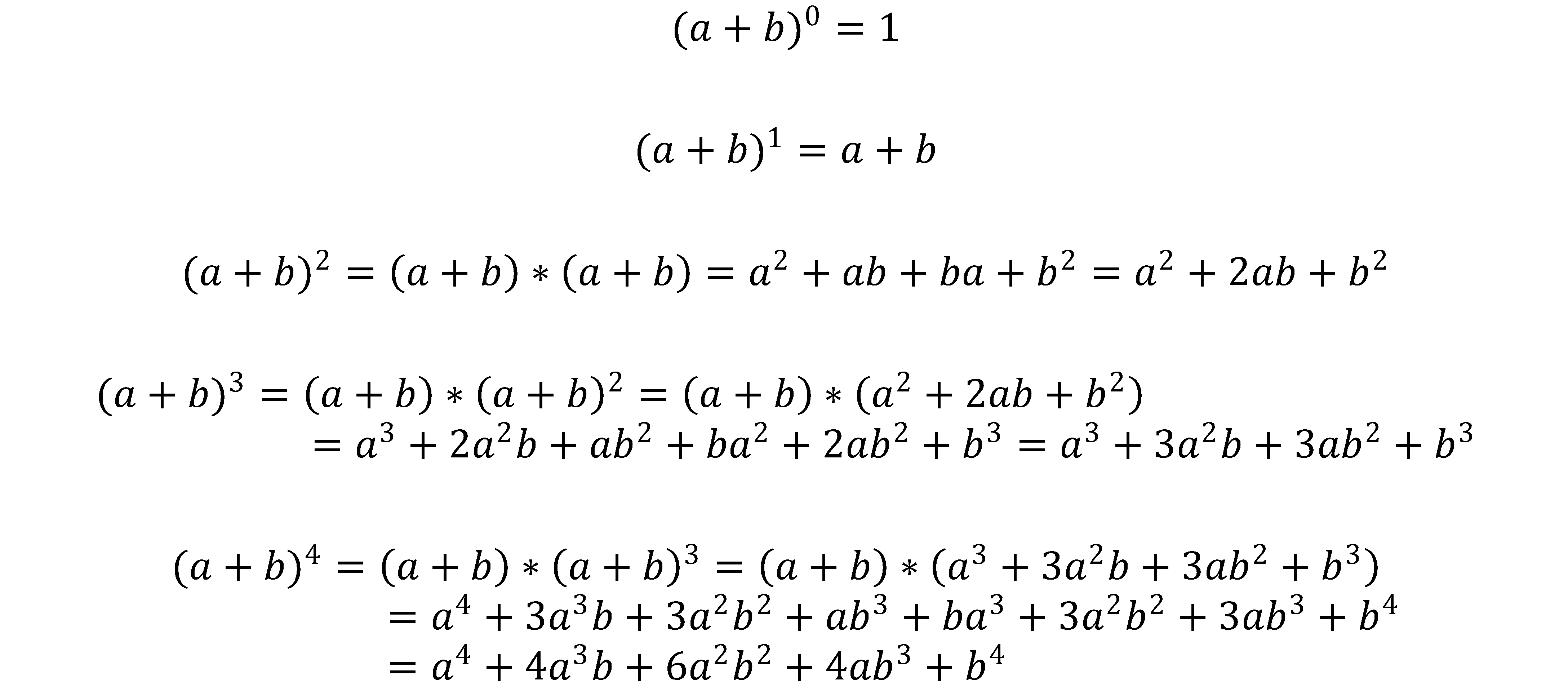
В общем виде то, что мы хотим вычислить, называется биномом Ньютона:
(a + b)n
Как видите, количество вычислений резко возрастает при увеличении степени.
Хотелось бы иметь способ быстрого вычисления коэффициентов при слагаемых в биноме Ньютона. И в этом нам поможет треугольник Паскаля. Он представляет собой пирамиду, в вершине которой находится 1, а каждая нижняя клетка равна сумме двух верхних клеток, которые на неё опираются (то есть треугольник Паскаля заполняется сверху):

Если строки треугольника нумеровать сверху, то числа в треугольнике являются коэффициентами при разложении бинома Ньютона. А какая же связь с комбинаторикой? Вернемся к задаче про салат. Там мы вычисляли количество сочетаний из 7 элементов по три:
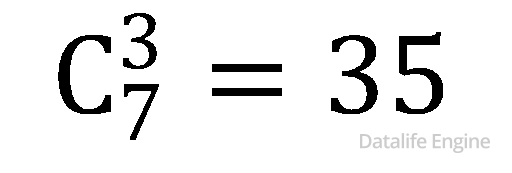
Если элементы строки тоже нумеровать с нуля, то посмотрите третий элемент в седьмой строке треугольника Паскаля. Это тоже 35. То есть коэффициенты при разложении бинома Ньютона являются сочетаниями.
Задача 2.2.4. Сколько шестибуквенных слов можно составить из букв A,B,C,D, если буква A встречается в каждом слове ровно три раза, а остальные буквы могут присутствовать в любых количествах или не быть вообще.
Определите вначале, сколько возможно расстановок буквы А (возможно, для этого нужно будет решить более простую задачу на размещение двух букв A или даже одной), затем определите, сколько возможно вариантов размещения других букв в оставшихся ячейках и свяжите результаты.
Для начала упростим задачу.
Упрощение 1. Пусть буква А встречается ровно 1 раз. В таком случае возможно 6 вариантов расположений буквы А:

В каждом из этих шести вариантов расположений имеется пять пустых ячеек для оставшихся трех букв B,C,D. По первой задаче в этой главе, возможно 3 * 3 * 3 * 3 * 3 слов. Поскольку такое количество будет в каждом из шести вариантов, то:
6 * 35 = 4374
Упрощение 2
Теперь рассмотрим, сколько существует расположений двух букв А. Возьмем первую строчку, где буква А находится в первой клетке, и расположим вторую букву А:
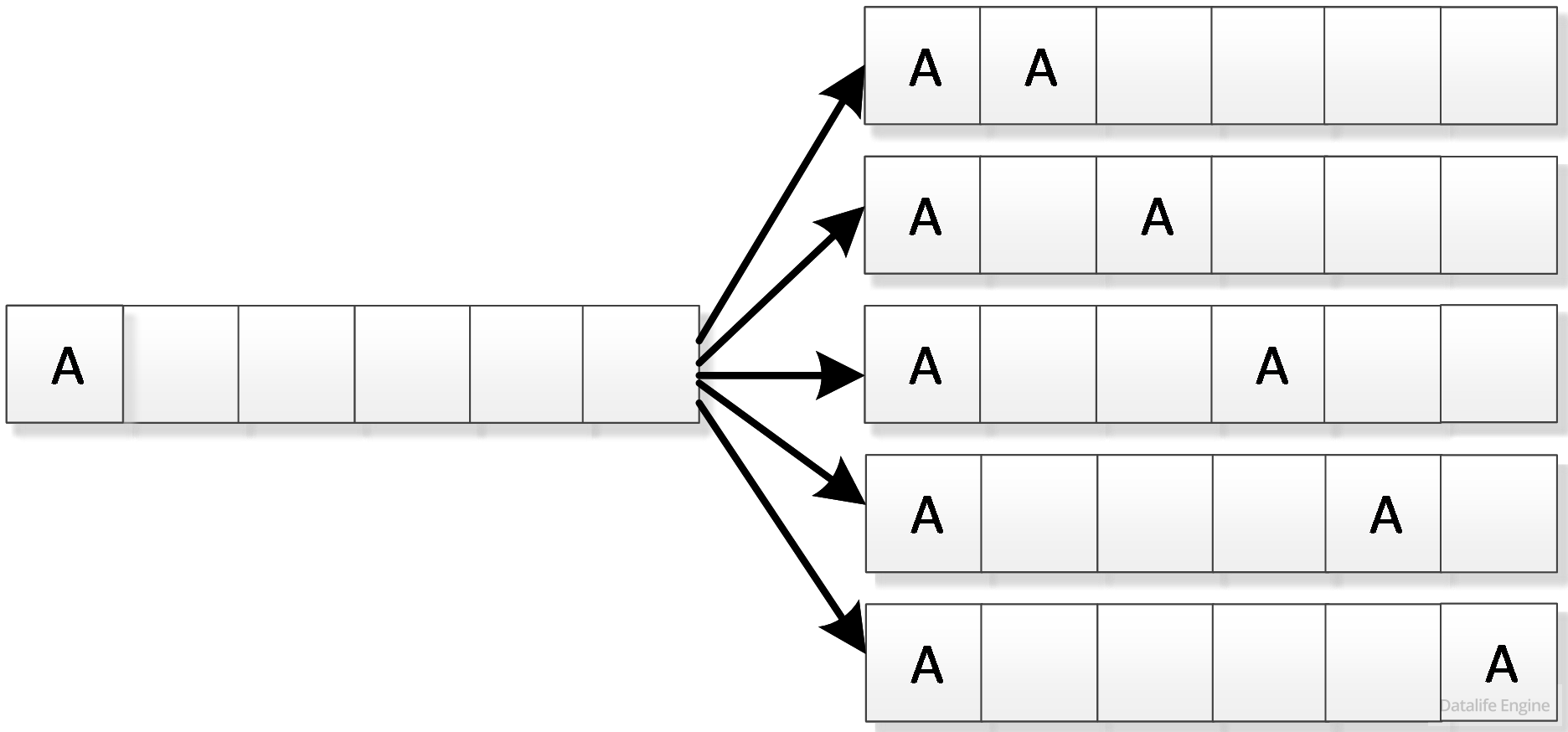
Возможно 5 вариантов расположения. Заметим, что расположение второй буквы А – это упрощенная задача 1.
Рассмотрим случай, когда первая буква А находится во второй ячейке. Сколько существует расположений второй буквы А?
Ошибка. Если вы ответили – 5, то вы ошиблись. Случай, когда вторая буква А находится на первом месте, мы уже сосчитали на предыдущем рисунке:

Продолжение хода решения:
Поэтому возможно лишь 4 расположения:
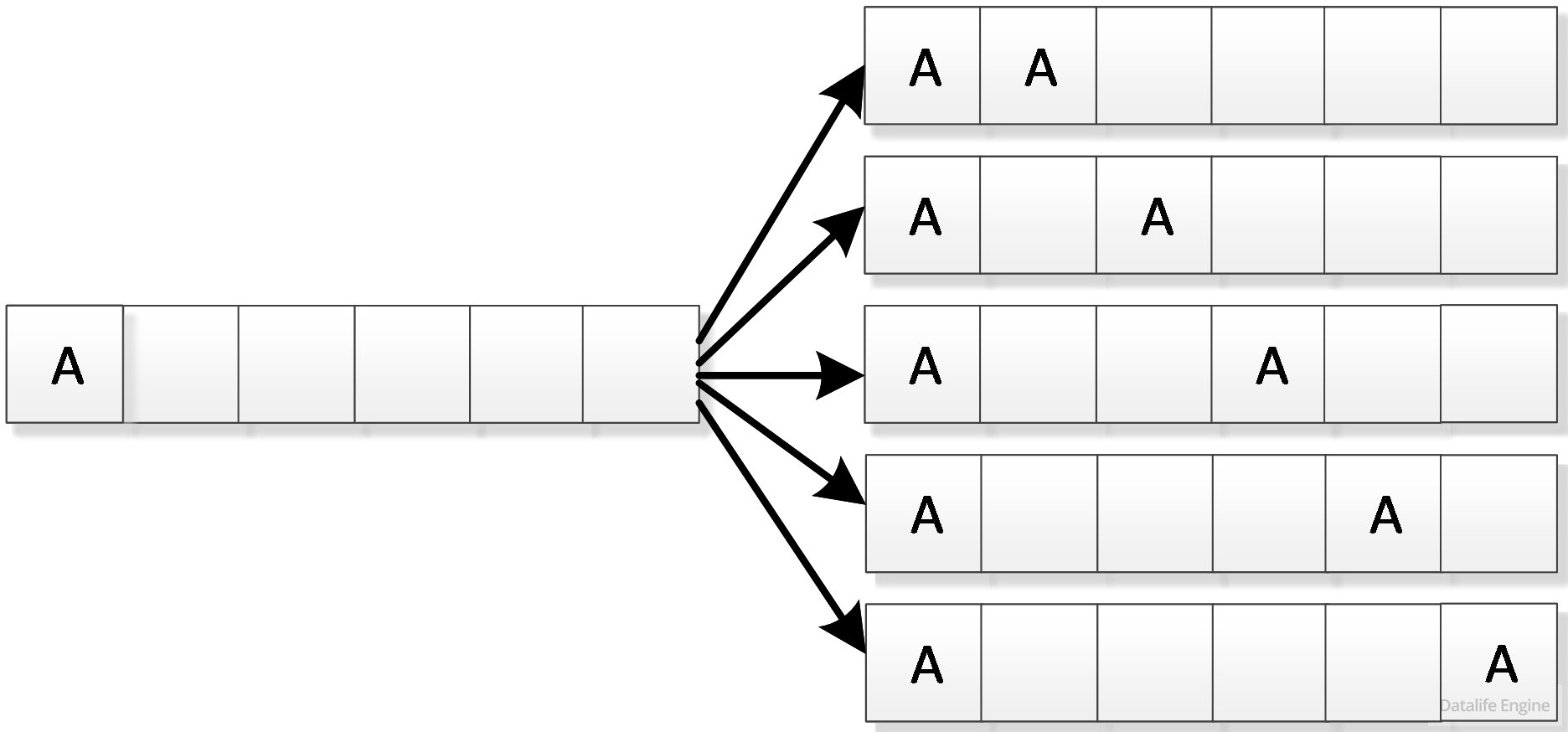
Соответственно, когда мы будем двигать первую букву А дальше, то для расположения второй буквы А будет всё меньше места:
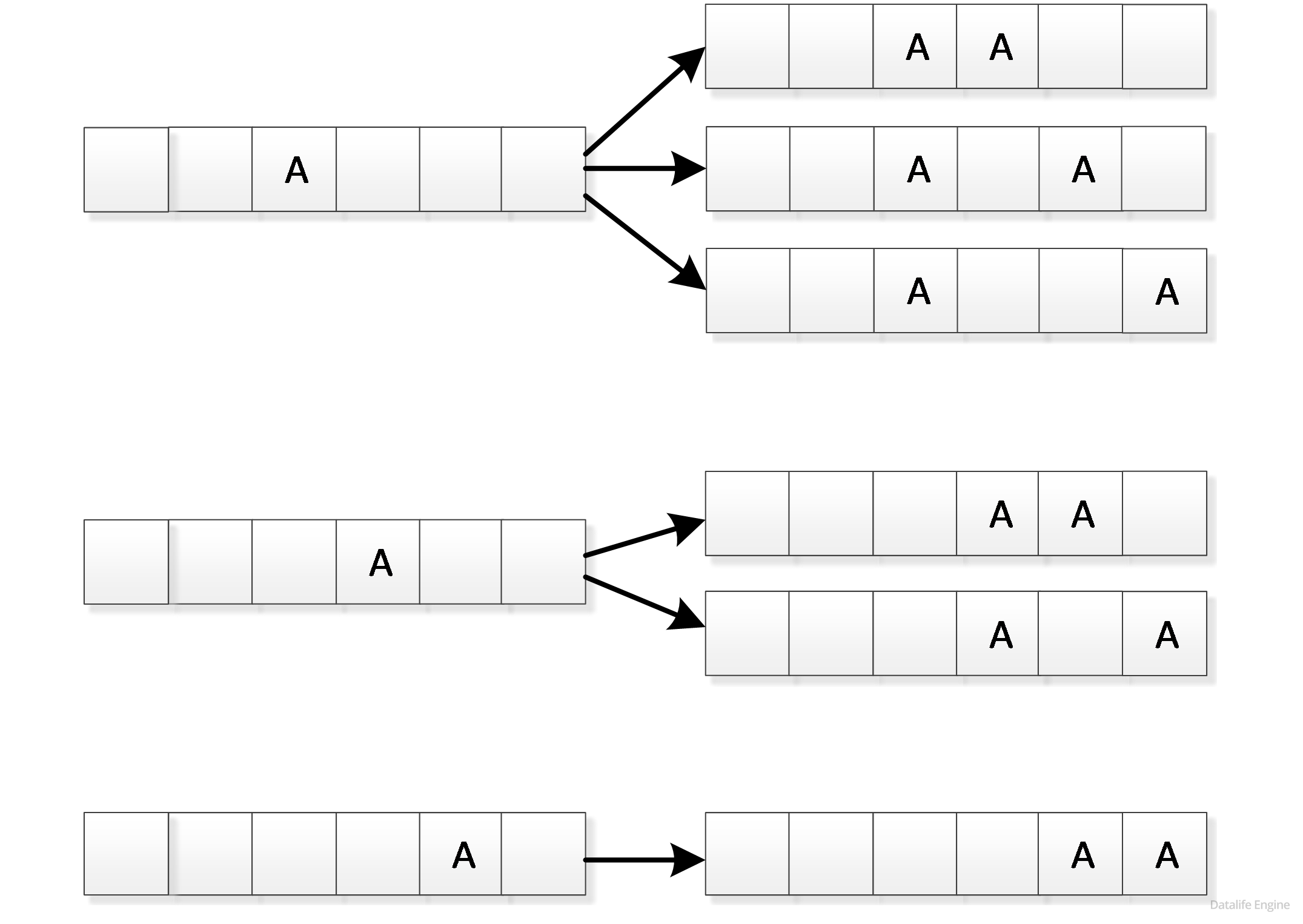
То есть количество расположений двух букв А по шести ячейкам равно:
5 + 4 + 3 + 2 + 1 = 15
В отличии от Упрощенной задачи 1, на остальные буквы осталось не 5, а 4 ячейки, поэтому количество возможных слов равно:
(5 + 4 + 3 + 2 + 1) * 34 = 1215
Примечание 1. Я уже говорил, что в ЕГЭ любят усложнять задачи. В нашем случае мы легко посчитали 5 + 4 + 3 + 2 + 1. Но в задаче, с которой вы столкнетесь, может оказаться слишком много членов ряда. Он представляет собой сумму членов арифметической прогрессии. В задаче 1.2.5. мы уже встречали арифметическую прогрессию? Вы уже выучили формулу для вычисления её суммы? Мы встретим прогрессии еще в некоторых задачах. Если не выучили, то, поскольку у нас принцип – меньше запоминать формул и больше запоминать ход решения, выведем формулу для суммы элементов арифметической прогрессии. Рассмотрим ряд:
1 + 2 + 3 + … + 10.
Разделим его пополам:
1 + 2 + 3 + 4 + 5 и 6 + 7 + 8 + 9 + 10
Начнем уменьшать элементы второй части и увеличивать элементы первой, чтобы общая сумма оставалась одинаковой:
1+2+3+5+5 и 6+6+8+9+10
1+2+5+5+5 и 6+6+6+9+10
1+5+5+5+5 и 6+6+6+6+10
5+5+5+5+5 и 6+6+6+6+6
Запишем вычисление нашей суммы и преобразуем её в формулу:
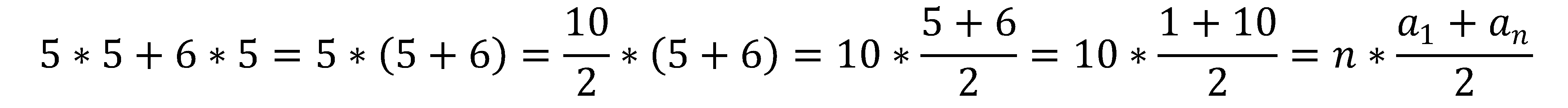
Ход решения основной задачи.
Потренировавшись на более простых случаях, теперь перейдем к условию основной задачи. Нужно разместить три буквы А по шести ячейкам.
Допустим, первая буква А расположена в первой ячейке:

Но тогда задачу расположения оставшихся двух букв А мы уже решили в упрощенной задаче 2 (только там на две буквы А было шесть ячеек, а теперь осталось 5). Следовательно, количество расположений двух букв А по пяти ячейкам равно:
4 + 3 + 2 + 1 = 10
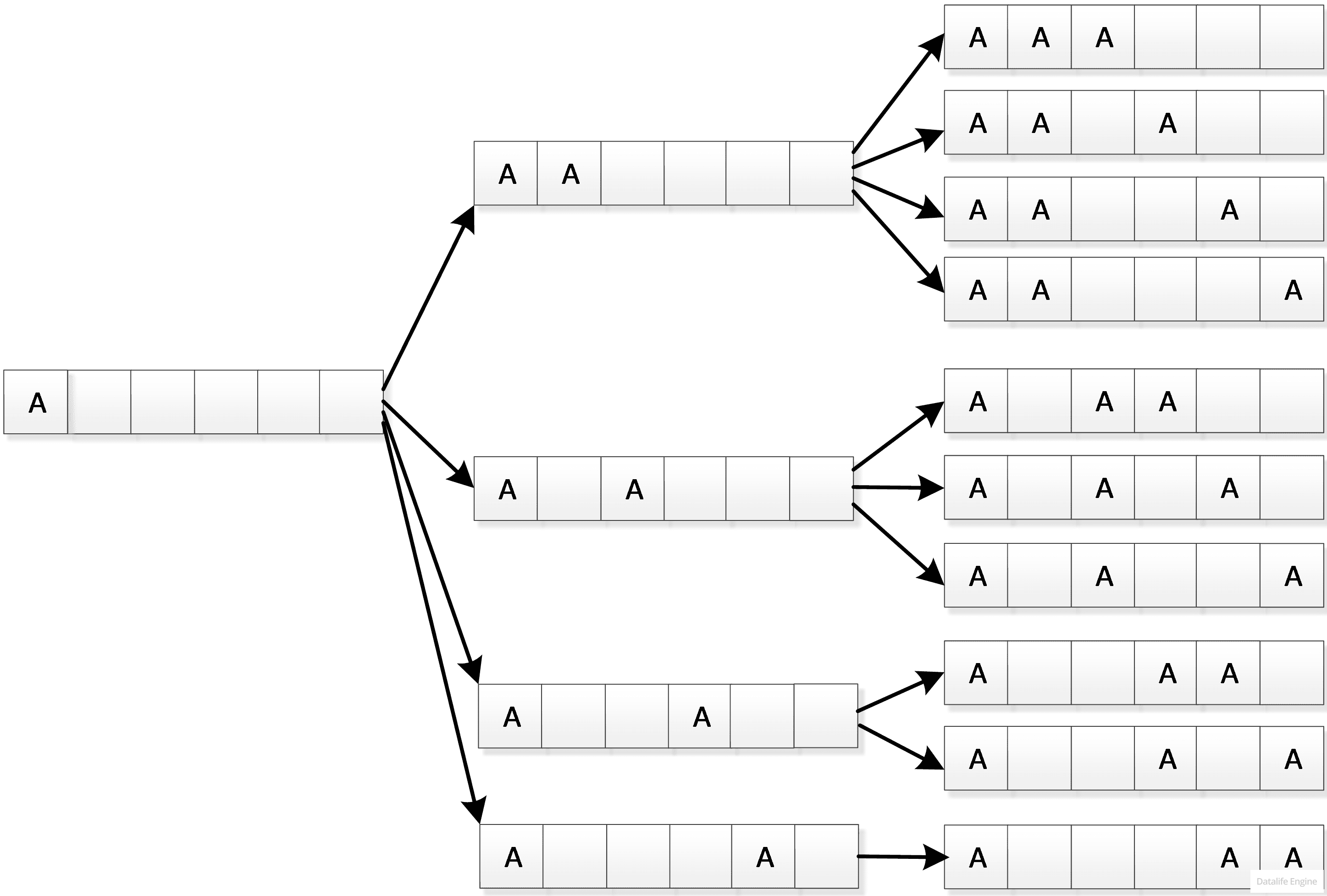
Сдвинем первую букву А на вторую позицию:

Для двух оставшихся букв А ячеек будет меньше, чем в предыдущем случае:
3 + 2 + 1 = 6
Для следующей позиции:

2 + 1 = 3
И, наконец, для

1
Для позиции:

Две буквы А уже просто не вместить
Таким образом, всего расположений трех букв А по шести ячейкам вычисляется так:
(4 + 3 + 2 + 1) +
(3 + 2 + 1) +
(2 + 1) +
1=
10 + 6 + 3 + 1 = 20
Примечание 2. Если мы усложним задачу и захотим расположить уже 4 буквы А по 6 ячейкам, то можно поступить, как мы делали раньше, то есть расположить первую букву А, а затем решать, сколько существует расположений 3 букв А по пяти ячейкам. Тогда нам надо будет сложить следующие «пирамидки»:
((3 + 2 + 1) +
(2 + 1) +
- +
((2 + 1) +
- +
(1)
=
6 + 3 + 1 +
3 + 1 +
1
=
10 + 4 + 1 = 15.
Но можно поступить и проще.
Посмотрите внимательно:

Намного проще уже двигать не буквы А, а пустые ячейки:
5 + 4 + 3 + 2 + 1 = 15
Результат тот же.
Примечание 3. Если мы сформулируем задачу в общем случае – разместить m букв А по n ячейкам, обозначив её за
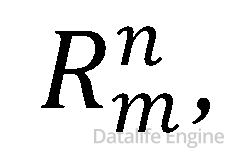
то, расположив первую букву А по n ячейкам, нам надо будет решать задачи с уменьшенным количеством букв А и уменьшенным количеством ячеек и сложить результаты:
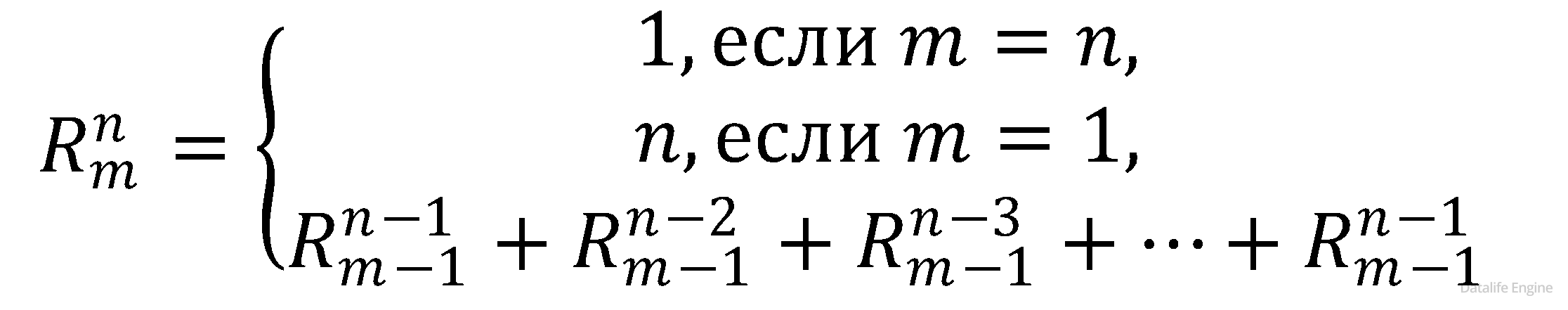
Например, в нашем случае
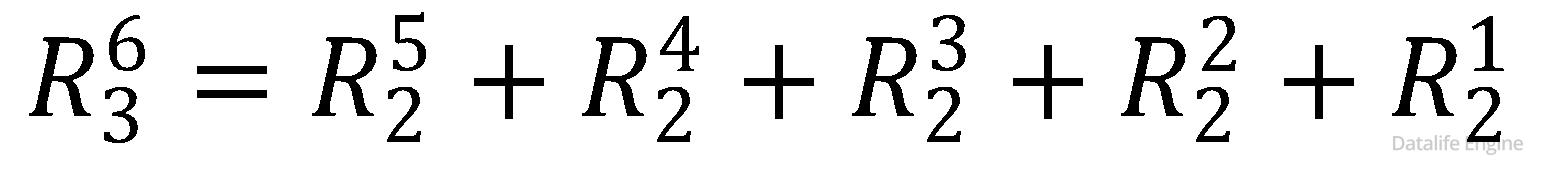
Такая ситуация, когда задача разбивается на подзадачи с уменьшенными входными данными, и эти подзадачи решаются подобно большой задаче, называется рекурсией. Эта задача – хоть и первый пример рекурсии, но достаточно сложный. В ЕГЭ есть простые задачи на рекурсию, которые мы будем изучать в разделе по программированию.
Примечание 4. Если мы рассмотрим количество расположений пяти букв А по шести ячейкам, то, очевидно, мы получим 6:

Если у нас шесть букв на шесть ячеек, то одно решение:

Посмотрим вычисленные результаты для расположений буквы А по шести ячейкам:
|
Кол-во букв А
|
1
|
2
|
3
|
4
|
5
|
6
|
|
Кол-во расположений
|
6
|
15
|
20
|
15
|
6
|
1
|
А теперь посмотрите на шестую строчку треугольника Паскаля. Количество расположений совпадает со строчкой треугольника Паскаля. То есть решения такие же, как и сочетания. И решить их можно намного быстрее с помощью треугольника Паскаля!
Задача 2.2.5. В соревновании принимали участие 20 спортсменов. Какой объем памяти (бит) нужен, чтобы запомнить номера трех победителей?
Это задача является обратной к задаче 2.2.1. Самый простой способ решения – подумайте, сколько спортсменов можно закодировать с помощью 1 бита, 2 битов, 3 …
Способ решения 1.
Поскольку мы не знаем, кто именно победит, нам нужно присвоить номера всем спортсменам. Поскольку мы храним номера спортсменов в битах, то это подобно тому, что мы будем на футболки спортсменам крепить номера, состоящие только из 0 и 1. Вопрос сводится к тому, какая будет длина номера.
Если бы у нас под номер был бы отведен один бит, то в соревновании смогли бы принять участие только два спортсмена – под номерами 0 и 1. Если два бита, то четыре спортсмена:
00
01
10
11
Добавим третий бит, получим 8 спортсменов:
000
001
010
011
000
001
010
011
Таким образом, каждый дополнительный бит удваивает количество спортсменов:
4 бита позволят присвоить номера 16 спортсменам, 5 бит – 32.
То есть для номеров 20 спортсменов нужно как минимум 5 бит.
Поскольку мы сохраняем номера трех победителей, то 3 * 5 = 15.
Способ решения 2.
Рассуждаем так же, как и в способе 1. Но решим задачу с помощью систем счисления. Поскольку спортсменов 20, то номера спортсменов лежат от 0 до 19. Переведем самый большой номер в двоичную систему:
|
19
|
2
|
|
|
|
|
1
|
9
|
2
|
|
|
|
|
1
|
4
|
2
|
|
|
|
|
0
|
2
|
2
|
|
|
|
|
0
|
1
|
То есть
1910 = 100112
Поскольку мы сохраняем номера трех победителей, то 3 * 5 = 15.
Способ решения 3.
Мы знаем формулу для количества слов:
w = mn
Где w-количество слов, m-мощность алфавита, n-количество ячеек.
В нашем случае w = 20 - количество спортсменов, m = 2, так как ячейка памяти принимает значения 0 и 1, n – количество ячеек – нам нужно найти.
n = logmw = log220
Поскольку логарифм точно не вычисляется, берем с запасом:
n = logmw = log232 = 5
Поскольку мы сохраняем номера трех победителей, то 3 * 5 = 15.
Ответ: 15 бит.
Ошибка из-за модификации задачи
Некоторые ученики рассуждают следующим образом: у нас есть 20 спортсменов, нужно выбрать троих из них. Спортсмены повторяться не могут (то есть один спорстмен не может занять сразу два места). Порядок имеет значение (то есть важно, какое именно место займет спортсмен). Поэтому применим формулу для размещения:
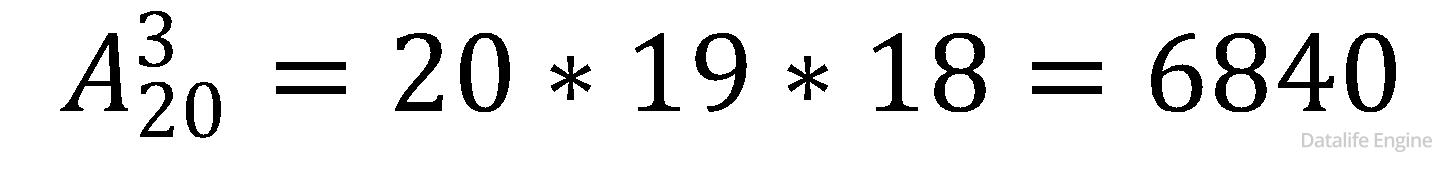
Но что мы найдем таким способом? Вовсе не количество памяти, необходимое для запоминания трех победителей, а количество вариантов списков чемпионов. Вот если бы была задача сделать заготовки поздравительных пресс-релизов с указанием фамилий победителей еще до проведения соревнований, то тогда бы количество пресс-релизов рассчитывалось бы таким способом.
Задача 2.2.6. Петя и Вася живут напротив друг друга и решили обмениваться сообщениями с помощью табло из лампочек. Каждая лампочка может быть выключенной, включенной или мигать. Сколько лампочек нужно, чтобы закодировать 33 буквы русского алфавита?
Задача подобна предыдущей, но вместо ячейки памяти, принимающей значения 0 и 1, в лампочке три состояния.
Можно решить любым способом предыдущей задачи. Решим первым способом:
Одна лампочка позволяет закодировать 3 буквы (обозначим их цифрами): 0,1,2
Две лампочки – 9 букв:
A – 00
Б – 01
В – 02
Г – 10
Д – 11
Е – 12
Ё – 20
Ж – 21
З – 22
Каждая следующая лампочка будет увеличивать количество букв в три раза:
3 * 3 * 3 = 27
3 * 3 * 3 * 3 = 81.
Таким образом, для кодирования букв русского алфавита нужно 4 лампочки.
Ответ: 4
Задача 2.2.7. В детскую игрушку «Набор юного шпиона» входят два одинаковых комплекта из четырех флажков различных цветов. Сколько различных тайных сообщений можно передать этими флажками, условившись менять выставленный флажок каждые пять минут и наблюдая за процессом 15 минут? Наблюдатель видит вынос первого флажка и две перемены флажка. При этом возможна смена флажка на флажок того же цвета.
В каждом вывешивании флажка определите, сколько различных видов флажков можно вывесить. В условии подразумевается, что есть только одна мачта, на которой в каждый момент висит только один флажок.
Первый вынос флажка: выбор из 4 цветов.
Второе вывешивание флажка: выбор из 4 цветов (так как у нас два комплекта флажков, то флажок может смениться на флажок того же цвета, но из другого набора).
Третье вывешивание флажка: выбор из 4 цветов (для того, чтобы три раза висели флажки одного цвета, три комплекта флажков не требуется, достаточно в третий раз выставить флажок, который висел в первый раз).
Итог: 4 * 4 * 4 = 64
Ответ. 64
Задача 2.2.8. Команды для некоторого устройства задаются тремя одинаковыми тумблерами. Сколько положений должно быть в тумблере, чтобы можно было закодировать 120 различных команд?
Эта задача является обратной к задаче 2.2.1.
Пусть x – количество положений в тумблере, тогда по задаче 2.2.1 количество кодируемых команд:
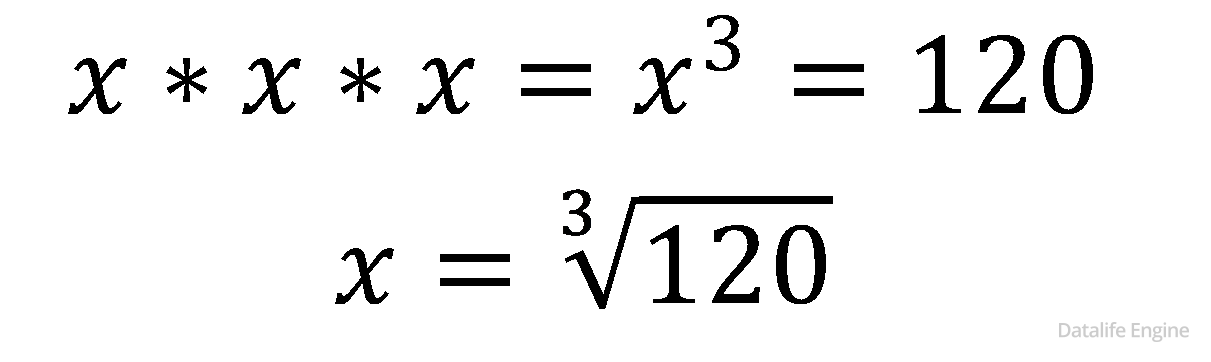
Округляем в большую сторону:
х = 5
Ответ. 5
Задача 2.2.9. Метеостанция измеряет температуру в диапазоне от -8 до 8 с точностью 0,5 градусов. Сколько бит нужно, чтобы сохранить результаты одного измерения?
Определите, сколько возможных состояний нужно закодировать, и дальше действуйте, как в двух предыдущих задачах.
Сперва посчитаем, сколько есть возможных температур. Для 8 это будет проблематично, поэтому сперва посчитаем на малом примере. Пусть температура изменяется от 1 до 2:

То есть 2 состояния.
В случае, если от 1 до 8, очевидно, будет 8 состояний.
Добавим точность 0,5:
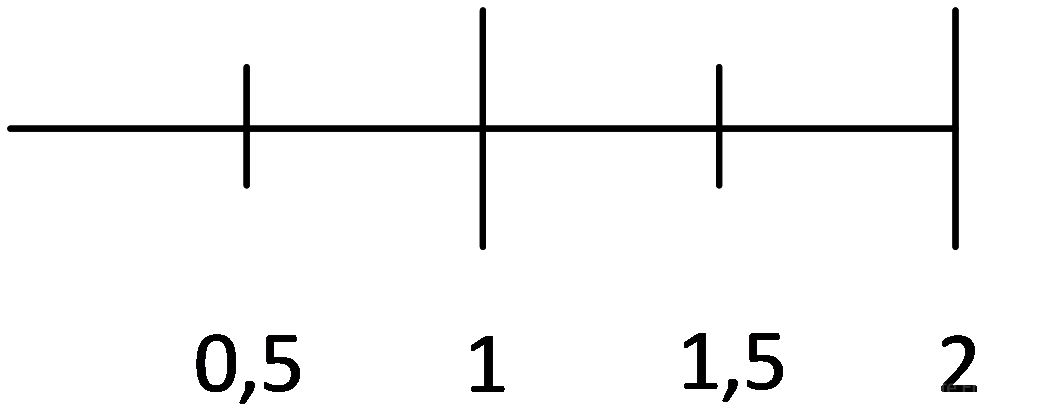
Количество состояний удвоилось.
В случае от 1 до 8 будет 16 состояний.
Добавим отрицательные состояния, и не забудьте про 0!
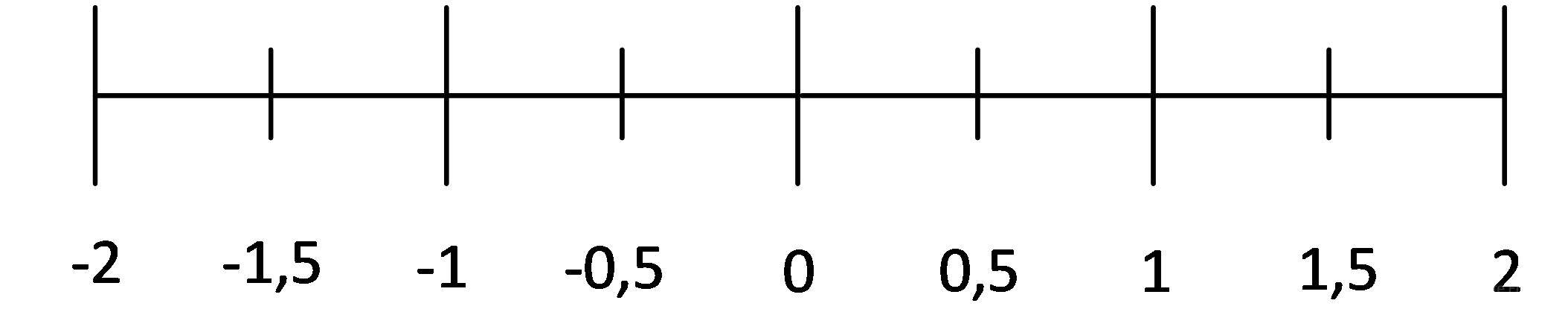
В случае от -8 до 8 с точностью 0,5 будет 16 * 2 + 1 = 33 состояний.
Для кодирования 33 состояний нужно 6 бит:
2 * 2 * 2 * 2 * 2 = 32 – не хватает
2 * 2 * 2 * 2 * 2 * 2 = 64
Ошибка 1. Иногда ученики забывают про состояние 0 и получают меньший результат.
Ошибка 2. Мы кодируем состояния, просто зная их количество. Будет ошибкой, если мы начнем переводить 8, а тем более –8 в двоичный вид. По большому счету, нам вообще не важен диапазон и точность, он мог бы быть и другим, но если в нем такое же число состояний, то код будет тем же самым:
–8 – 000000
–7,5 – 000001
–7 – 000010
–6,5 – 000011
…
Ответ: 6 бит
Задача 2.2.10. Какой объем памяти в байтах нужен, чтобы сохранить картинку размером 8X8 пикселей, при использовании палитры из 32 цветов?
Задача похожа на задачу о спортсменах, только вместо спортсменов у нас идут 32 цвета, которые нужно закодировать.
Для кодирования 32 цветов нам нужно:
n = log232 = 5 бит
Всего пикселей 8*8 бит, на каждый пиксель отводится 5 бит, результат нужен в байтах:
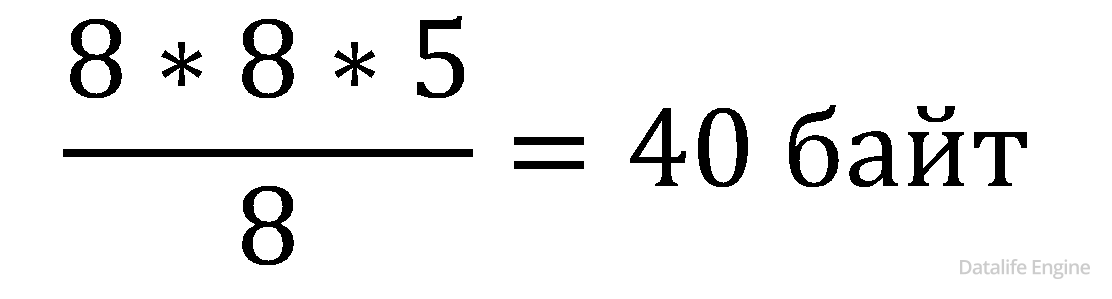
Ошибка. Было бы неправильно считать так:
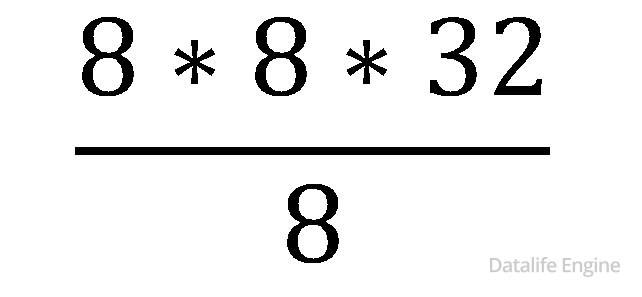
Часто правильность формулы можно проверить, подставив единицы измерения. В ошибочном случае будут цвета, деленные на биты.
Также понять ошибку можно на более простом примере. Допустим, у нас черно-белое изображение. Но это не значит, что нужно количество пикселей умножать на 2. Ведь нам достаточно одного бита с двумя состояниями на пиксель: 0 – черный цвет, 1- белый.
Ответ: 40.
Ошибка из-за модификации задачи
Иногда ученики рассуждают следующим образом: количество ячеек равно
8 * 8 = 64. 32 цвета – это мощность алфавита. Следовательно, применим степенную формулу:
3264 = ?!!
Но что мы найдем таким образом? Количество всех возможных картинок! Это совсем другая задача. Мы не ищем количество всех возможных картинок, а определяем, сколько бит надо для сохранения одной картинки.
Трудность комбинаторных задач заключается в том, что не надо понимать входные данные задачи слишком буквально. В нашем случае:
- Количество цветов – это не мощность алфавита. Поскольку мы сохраняем изображение в битах, то мощность алфавита равна 2.
- Количество пикселей – это не количество ячеек. Подвох задачи в том, что нам по количеству цветов надо посчитать количество ячеек на один пиксель.
Задача 2.2.11. Производится двухканальная звукозапись с частотой дискретизации 100 Гц. При записи использовались 256 уровней дискретизации. Запись длится 5 минут. Сколько байт требуется для сохранения звукозаписи?
Несмотря на то, что задача из другой предметной области, она решается аналогично предыдущим задачам. Вам нужно найти аналоги: что именно соответствует цвету, количеству спортсменов и т.д. в этой задаче.
Сперва разберемся, что значит двухканальная запись. Это означает, что у нас два различных сигнала – для правой колонки и для левой. Таким образом, нам надо посчитать объем памяти для одного сигнала и удвоить результат:
2 * …
Теория 1. Теперь поймем, что такое частота дискретизации, измеряемая в Герцах. Поскольку физику обычно преподают лучше, чем информатику, ученики говорят, что частота – это количество колебаний маятника (то есть количество движений маятника из одного крайнего положения в другое и обратно) в секунду и вспоминают, что
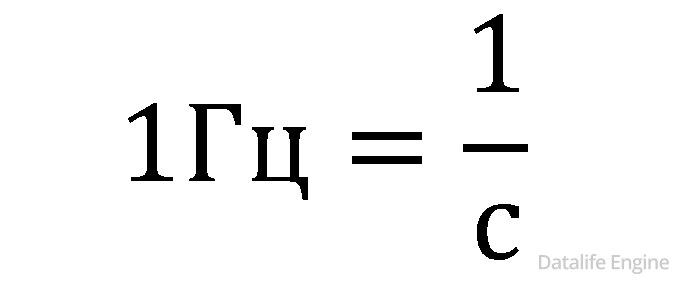
Частоту дискретизации с частотой колебаний маятника роднит только эта формула для единиц измерения. Рассмотрим сигнал:
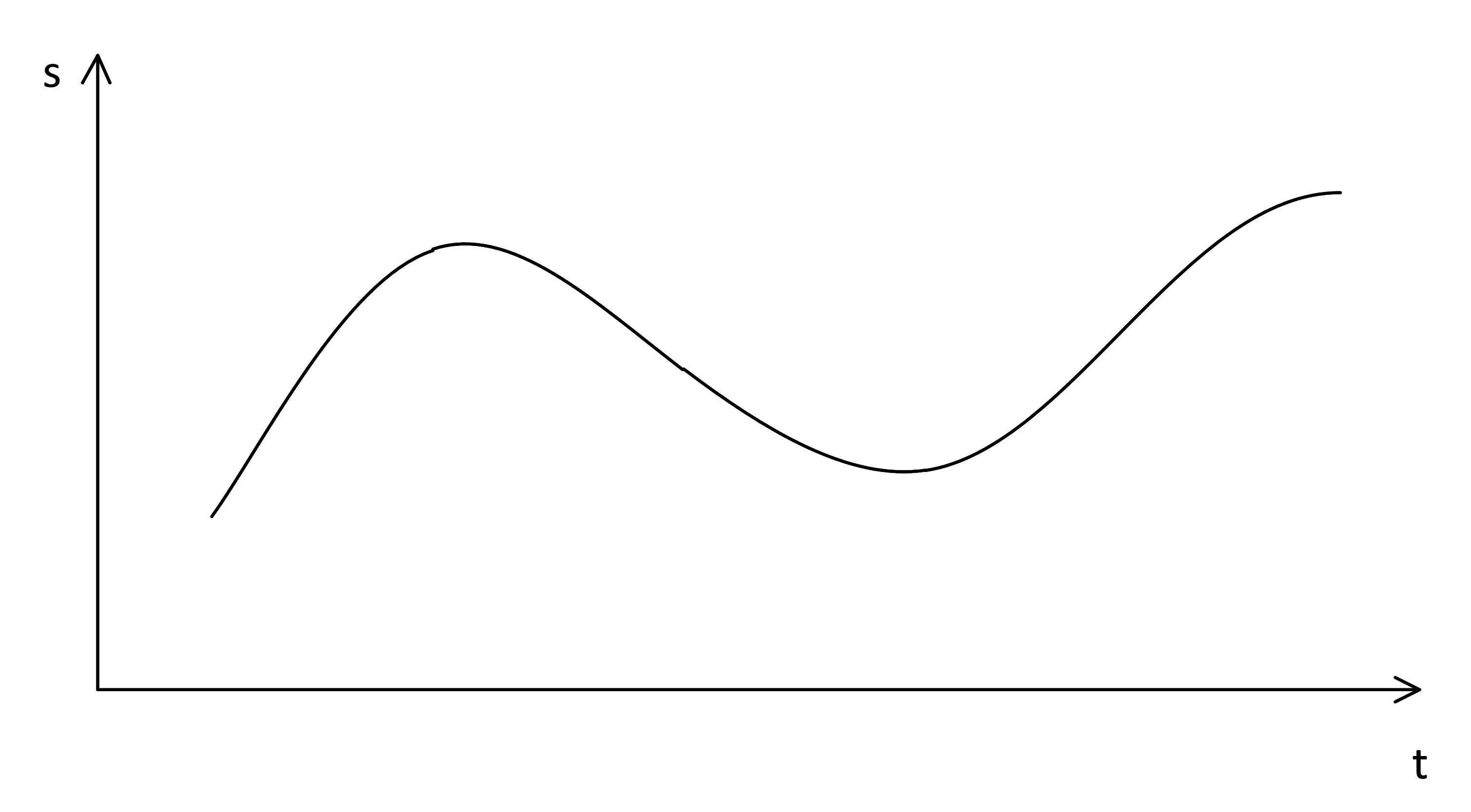
Есть мало устройств, которые обрабатывают сигналы в непрерывном виде (такие устройства называются аналоговыми). В большинстве случаев сигналы обрабатываются в дискретном виде (цифровые устройства). Это означает, что сигнал не обрабатывается непрерывно, а снимаются отсчеты сигнала с некоторой периодичностью:
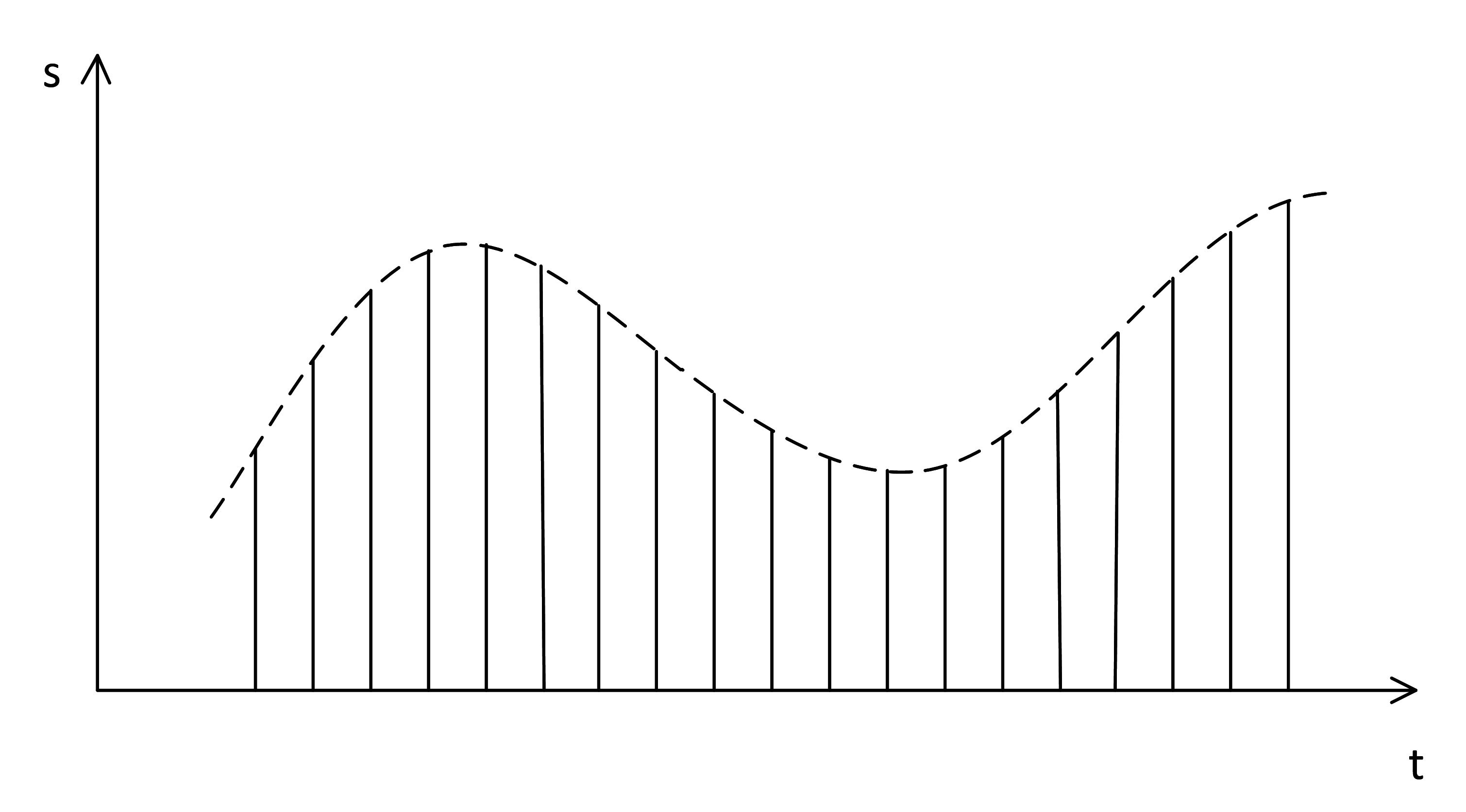
Частота дискретизации – это количество отсчетов сигнала за одну секунду.
Продолжение хода решения
Поскольку запись длится 5 минут, а частота дискретизации дана в Герцах, то продолжим наши вычисления:
2 * 100 * 5 * 60 * …
Теория 2. Что такое уровни дискретизации? Каждый отсчет современные устройства в большинстве случаев хранят также в цифровом виде. То есть мы знаем не точное значение природного сигнала, а примерное, в соответствии с отведенной на него памятью:
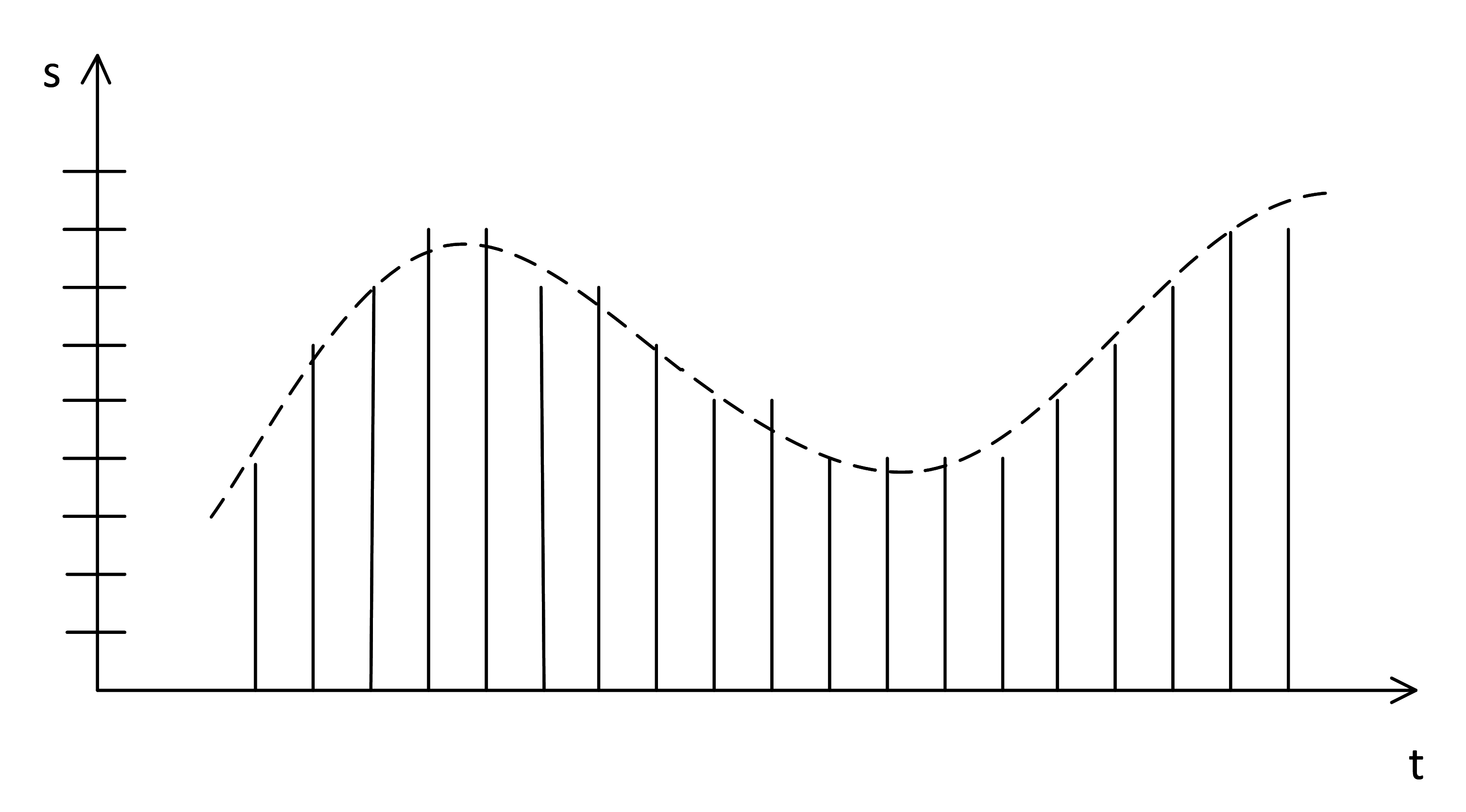
И вот эти уровни дискретизации нужно закодировать, как в задаче с температурой или цветной картинкой.
Продолжение хода решения
Поскольку в задаче 256 уровней дискретизации, то объем памяти в битах на один отсчет будет равен:
log2256 = 8
Продолжаем вычисления:
2 * 100 * 5 * 60 * 8
Поскольку ответ нужен в байтах:
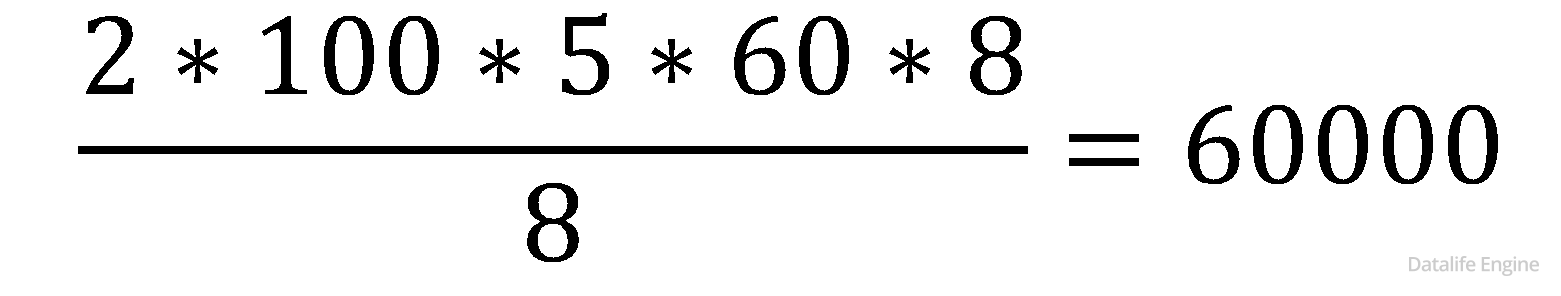
Ответ: 60000.
Примечание. Приведенная задача может быть сформулирована и другими способами: 1. Вместо уровней дискретизации может быть приведен диапазон изменения величины и точность, как в задаче с метеостанцией 2.2.6. В этом случае надо посчитать количество уровней дискретизации и закодировать их.
2. Задача может быть приведена и в упрощенном виде. Вместо уровней дискретизации сразу может быть приведен объем памяти в битах на один отсчет. То есть для нашего случая вместо 256 уровней дискретизации сразу будет дано 8 бит.
Задача 2.2.12. Производится одноканальная (моно) звукозапись с частотой дискретизации 48 кГц и глубиной кодирования 16 бит. Запись длится 2 минуты, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?
1) 11
2) 12
3) 13
4) 20
Задача подобна предыдущей, но использует примерные вычисления и другие единицы измерения, поэтому мы приводим её в этой книге.
Теория.
Приведем различные единицы измерения:
1 байт = 8 бит = 23 бит
1 Килобайт = 1024 байта = 210 байта = 213 бит
1 Мегабайт = 1024 Килобайта = 210 Килобайта = 220 байт = 223 бит
1 Терабайт = 1024 Мегабайта = 210 Мегабайта = 220 Килобайт = 230 байт = 233 бит
Терабайты в ЕГЭ до сих пор не встречались, но, поскольку появились жесткие диски на такой объем памяти, то весьма вероятно, что эта единица измерения также появится в ЕГЭ.
Обратите внимание, что вместо 1000 при переводе из одной единицы измерения в другую используется множитель 1024. Так удобнее в информатике. При примерных подсчетах 1000 и 1024 можно сокращать.
Ошибка. Школьная физика приучила решать задачи по шагам. Но этот путь приведет к громоздким вычислениям. Правильный способ решения – записать итоговую формулу, подставить числа, потом сокращать.
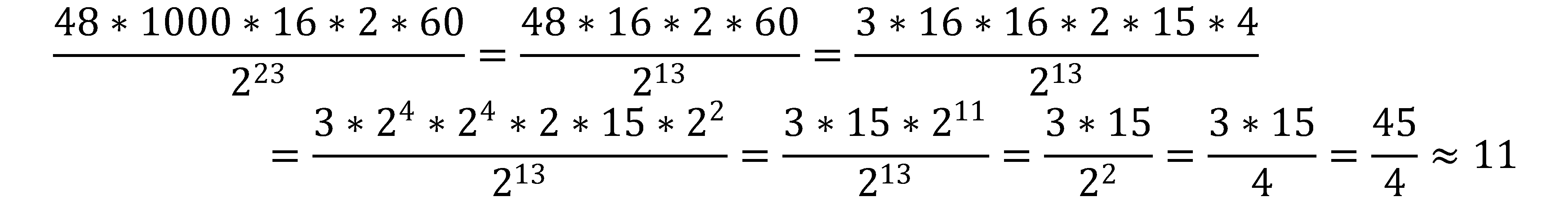
Ответ: 11
Задача 2.2.13. B некоторой стране автомобильный номер длиной 7 символов составляют из заглавных букв (используются только 33 различных буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов). Определите объём памяти, отводимый этой программой для записи 125 номеров.
Посчитайте, сколько бит нужно, чтобы закодировать один символ, зная мощность алфавита. Потом определите количество бит на один номер, потом количество байтов на один номер, затем количество байтов на все номера.
Поскольку используются 33 буквы и десятичные цифры, то мощность алфавита равна
33 + 10 = 43
Посчитаем объем памяти в битах на один символ:
log243 < log264 = 6
Если вы забыли эту формулу, то, согласно задаче 2.2.5, каждый дополнительный бит удваивает количество кодируемых объектов, то есть 1 бит позволяет закодировать 2 объекта, 2 бита – 4 объекта, 3 бита – 8 объектов и т.д. Таким образом, 5 бит недостаточно, так как они позволяют закодировать только 32 буквы, а 6 хватит с избытком.
Поскольку номер состоит из 7 символов, то количество бит на номер равно:
6 * 7 = 42
Так как каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов, то переведем 42 в байты и округлим в большую сторону до целого числа:
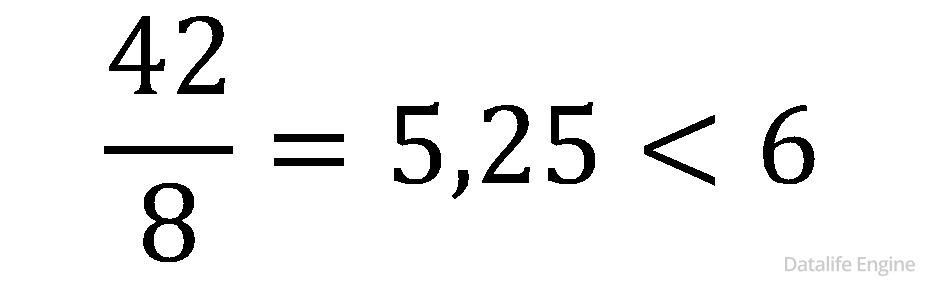
Посчитаем количество байт на 125 номеров:
6 * 125 = 750
Ответ: 750
Ошибка из-за модификации задачи
Иногда ученики рассуждают следующим образом: количество ячеек равно 7. Мощность алфавита 33 + 10 = 43. Следовательно, применим степенную формулу:
437 = ?!!
Но что мы найдем таким образом? Количество всех возможных автомобильных номеров! Это совсем другая задача (ошибка сродни той, которая приводилась в задаче на объем картинки).
Задача 2.2.14. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 480 бит. Какова длина сообщения в символах?
Если не вдаваться в подробности того, как устроены разные кодировки, то, зная, что в Unicode отводится 16 бит на символ, а в КОИ-8 – 8 бит на символ, составьте и решите уравнение.
Пусть x – длина сообщения в символах, тогда:
16х - длина в битах сообщения в кодировке КОИ-8,
8x – длина в битах сообщения в кодировке КОИ-8.
Поскольку сообщение уменьшилось на 480 бит:
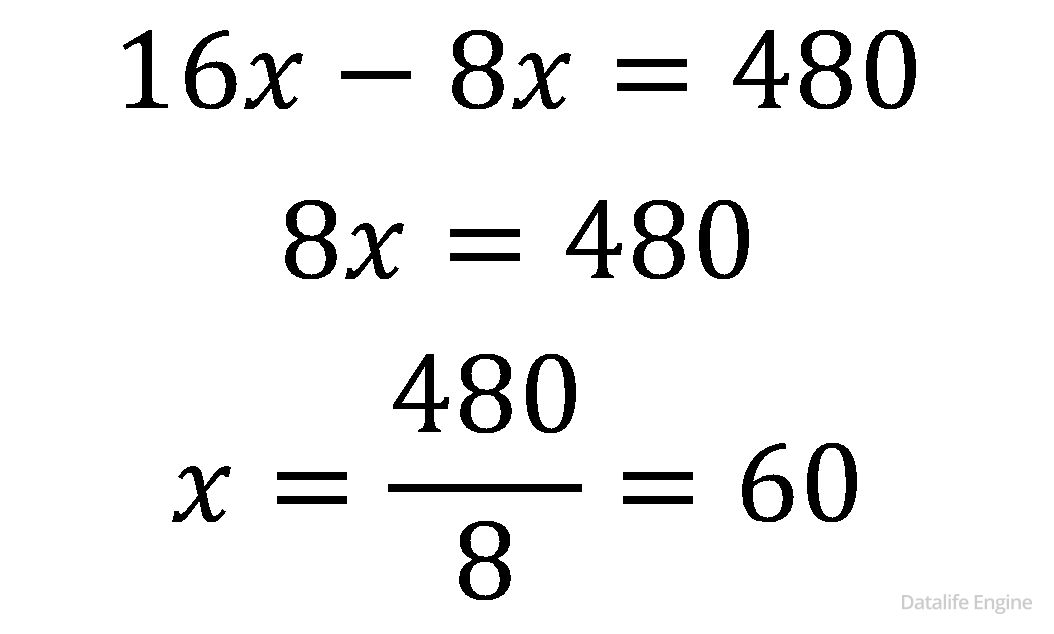
Ответ: 60
Задача 2.2.15. Герасим составляет 7-буквенные коды из букв Г, Е, Р, А, С, И, М. Каждую букву нужно использовать ровно 1 раз, при этом нельзя ставить подряд две гласные или две согласные. Сколько различных кодов может составить Герасим?
Решайте задачу аналогично задаче 2.2.2.
Согласных букв 4, гласных букв 3. Так как подряд нельзя ставить две гласные и две согласные, то гласные и согласные чередуются. Так как слово семибуквенное, то первой буквой идет согласная (иначе гласных не хватит):
|
согласная
|
гласная
|
согласная
|
гласная
|
согласная
|
гласная
|
согласная
|
Так как буквы не могут повторяться, то способ вычисления будет по типу факториала (если бы не было никаких ограничений на буквы, то количество слов равнялось бы 7 * 6 * 5 * 4 * 3 * 2 * 1) – количество вариантов букв убывает при добавлении всё новой буквы (см. задачу 2.2.2).
Так в первых двух буквах у нас выбор из четырех согласных и трех гласных:
|
|
согласная
|
гласная
|
|
Количество
вариантов букв
|
4
|
3
|
При добавлении следующих двух букв, так как одну согласную и одну гласную мы уже израсходовали, то количество вариантов уменьшается:
|
|
согласная
|
гласная
|
согласная
|
гласная
|
|
Количество
вариантов букв
|
4
|
3
|
3
|
2
|
При добавлении новых букв выбор продолжает уменьшаться:
|
|
согласная
|
гласная
|
согласная
|
гласная
|
согласная
|
гласная
|
согласная
|
|
Количество
вариантов букв
|
4
|
3
|
3
|
2
|
2
|
1
|
1
|
Из предыдущих задач следует (см. задачи 2.2.1 и 2.2.2), что количество вариантов надо перемножить: 4 * 3 * 3 * 2 * 2 * 1 * 1 = 144
Ответ: 144.
Задача 2.2.16. Левий составляет 5-буквенные коды из букв Л, Е, В, И, Й. Каждую букву нужно использовать ровно 1 раз, при этом код не может начинаться с буквы Й и не может содержать сочетания ЕИ. Сколько различных кодов может составить Левий?
Решайте задачу аналогично задаче 2.2.2. Посчитайте количество решений без ограничения на ЕИ, затем вычтите количество вариантов с ЕИ.
Посчитаем количество вариантов для каждой буквы. Поскольку буквы не повторяются, то при добавлении новых букв количество вариантов сокращается:
|
Номер буквы
|
1
|
2
|
3
|
4
|
5
|
|
Количество вариантов букв
|
4
|
4
|
3
|
2
|
1
|
Так как на первом месте не может быть и-краткой, то для первой буквы выбор только из 4 букв.
Количество возможных слов: 4 * 4 * 3 * 2 * 1 = 96
Рассмотрим теперь ограничение ЕИ. Пусть эти буквы стоят на первом и втором месте:
|
Номер буквы
|
Е
|
И
|
3
|
4
|
5
|
|
Количество вариантов букв
|
1
|
1
|
3
|
2
|
1
|
Количество слов, которые можно составить, когда ЕИ в начале равно 3 * 2 * 1.
Пусть ЕИ стоят на втором и третьем месте:
|
Номер буквы
|
1
|
Е
|
И
|
4
|
5
|
|
Количество вариантов букв
|
2
|
1
|
1
|
2
|
1
|
Количество слов равно 2 * 2 * 1 = 4.
Аналогично количество слов равно 4 при расположениях ЕИ:
|
Номер буквы
|
1
|
2
|
Е
|
И
|
5
|
|
Количество вариантов букв
|
2
|
2
|
1
|
1
|
1
|
|
Номер буквы
|
1
|
2
|
3
|
Е
|
И
|
|
Количество вариантов букв
|
2
|
2
|
1
|
1
|
1
|
Общее количество слов с учетом всех ограничений равно: 96 – 6 – 4 * 3 = 78
Ответ. 78
Комбинаторика «пронизывает» весь ЕГЭ. Мы неоднократно встретимся с приемами этого параграфа в задачах на графы и деревья, логические уравнения и IP-адресацию. Предпоследняя глава книги «Комбинаторика» содержит как комбинаторные задачи на повторение из всех разделов ЕГЭ, так и задачи повышенной сложности.