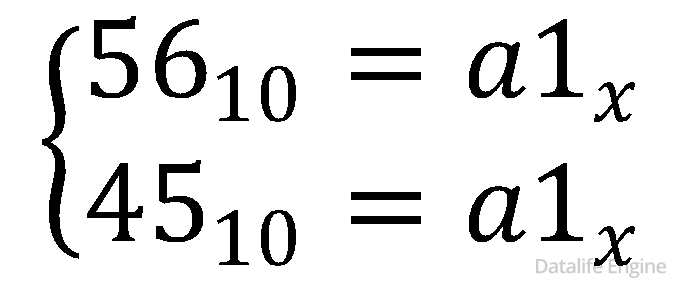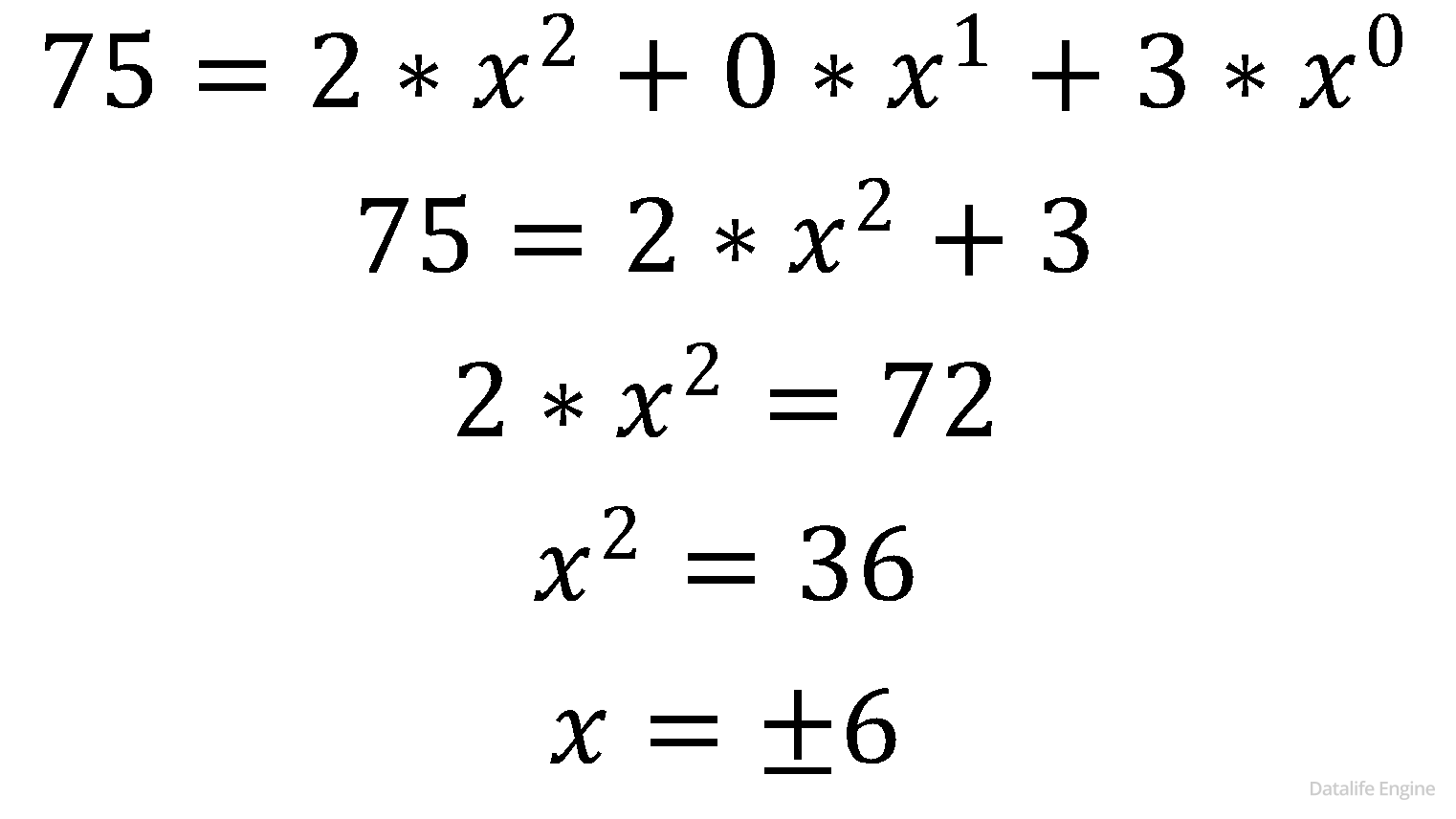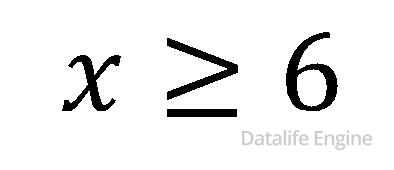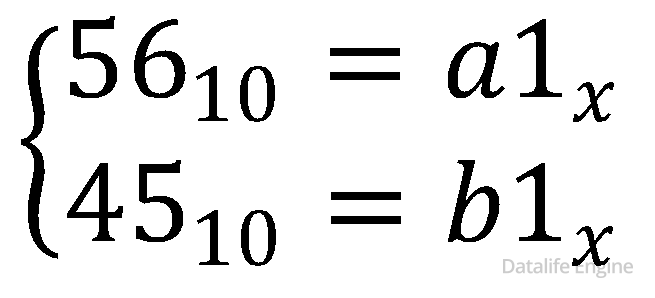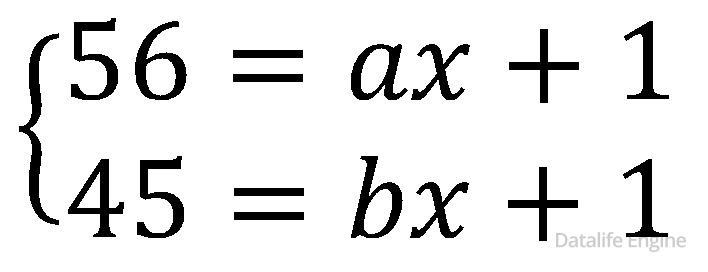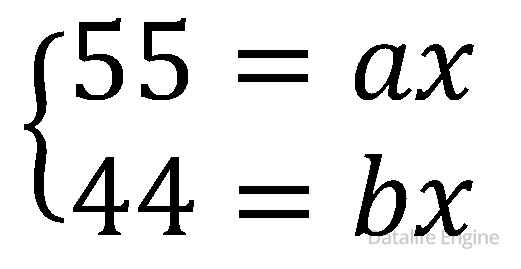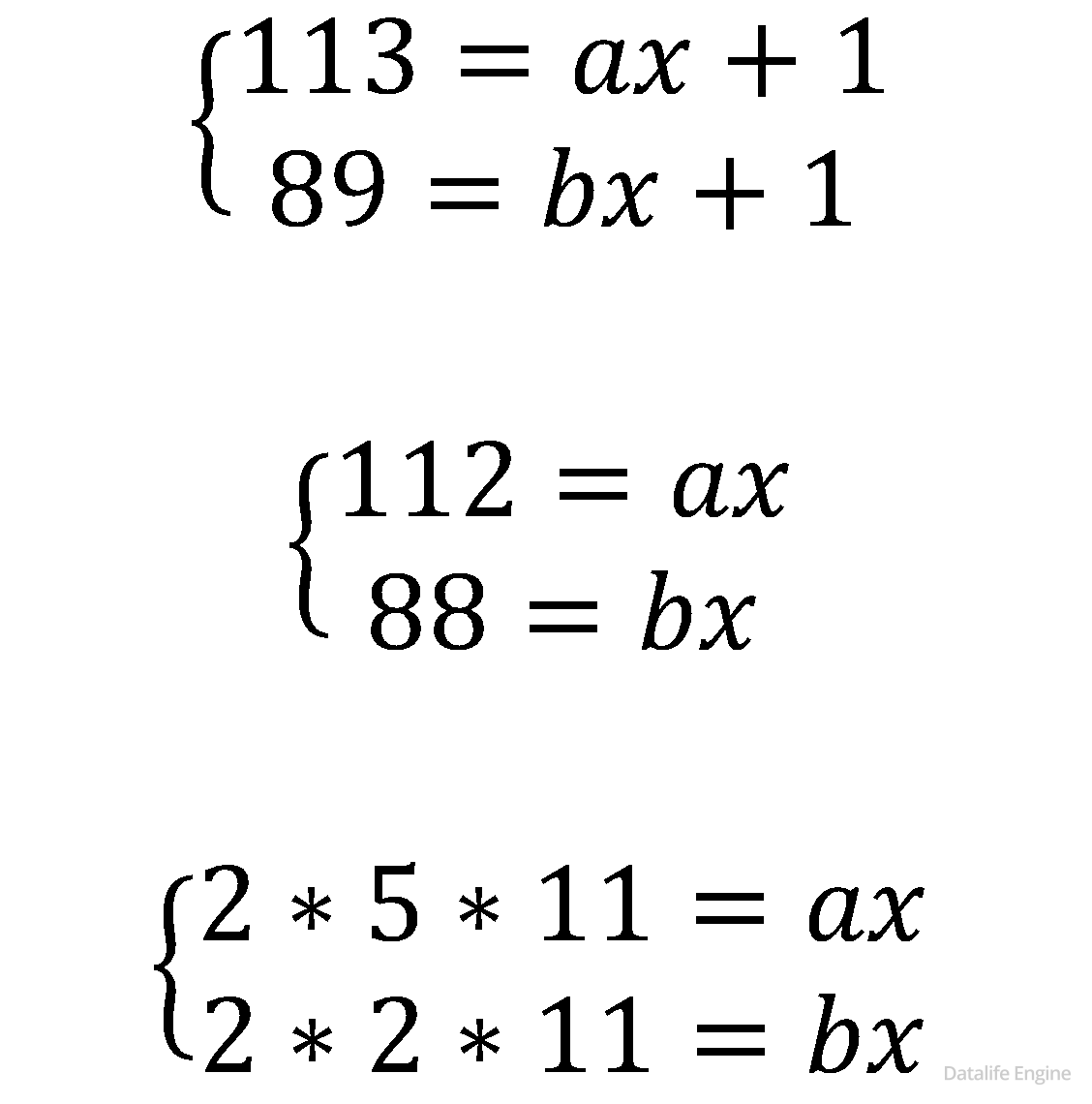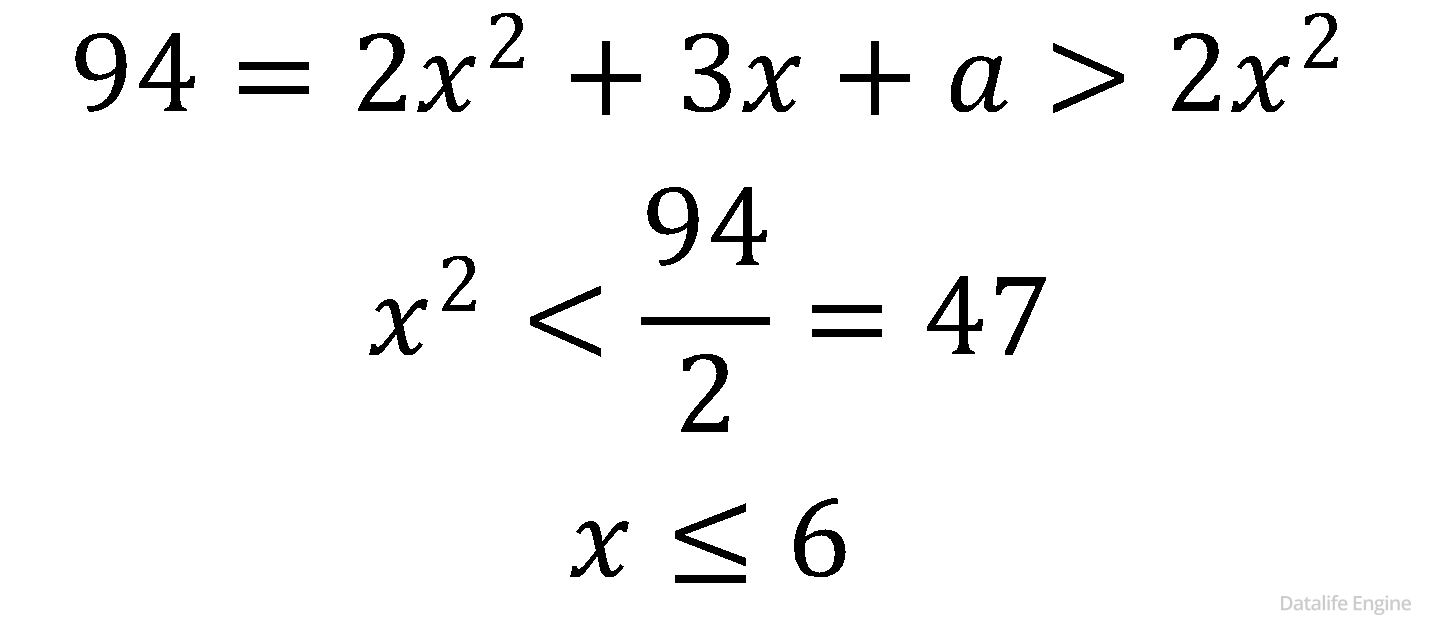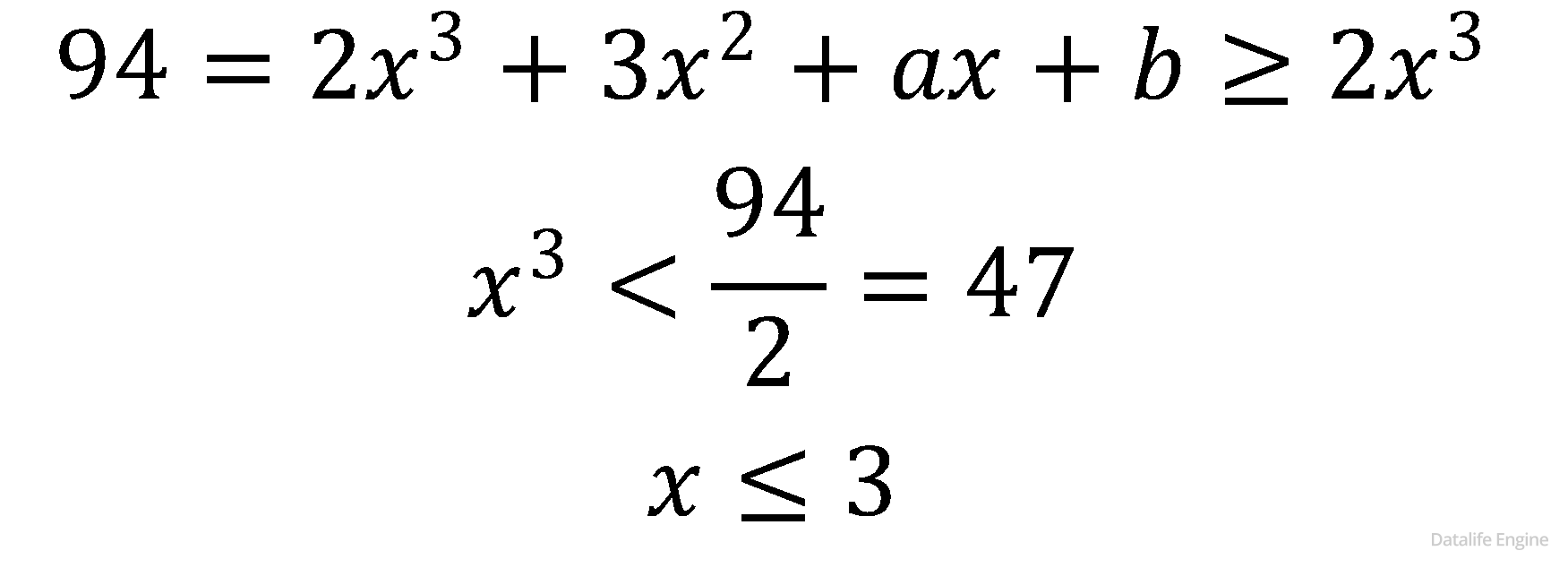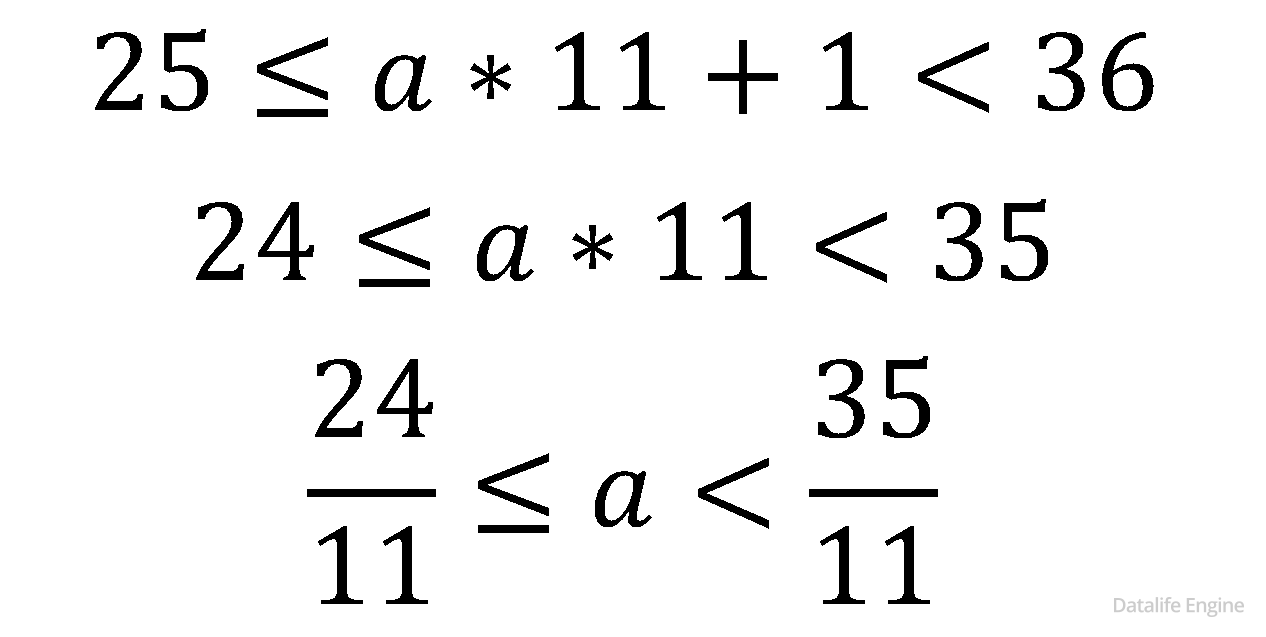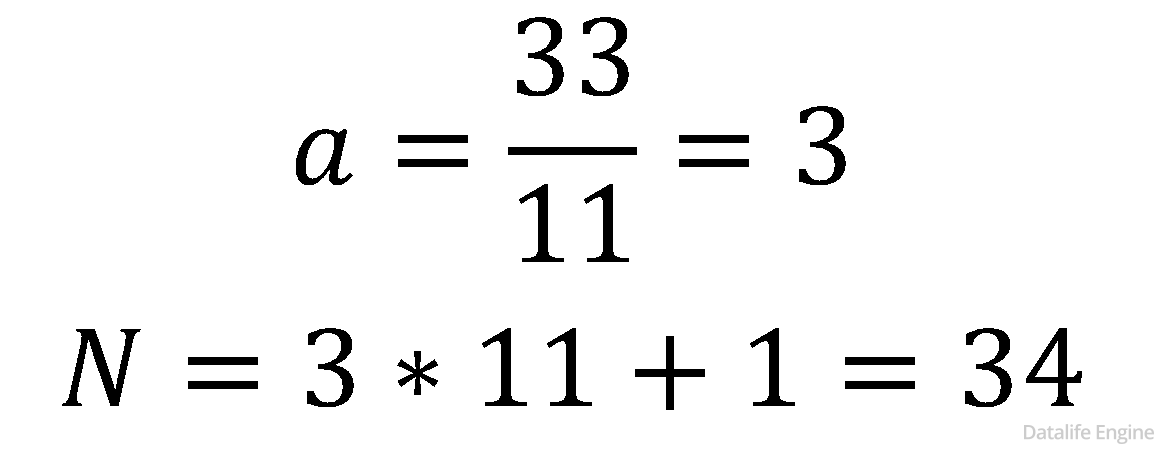В предыдущих задачах основания системы счисления были даны в условии. Следующая группа задач содержит неизвестные основания систем счисления, которые нужно найти.
Задача 1.6.1. В системе счисления с некоторым основанием десятичное число 75 записывается в виде 203. Укажите это основание.
Это задача проверяет, есть ли у ученика математическая культура. Что мы делаем, если что-то неизвестно? Обозначаем эту величину буквой и записываем уравнение. Примите за х неизвестное основание и составьте уравнение. Подумайте о применении прямого или обратного перевода.
7510 = 203х
Дальше есть два пути – прямой перевод и обратный. Прямой перевод из десятичной в x-ичную вряд ли полезен, так как каскадно делить на x – это очень странно. А вот наоборот – легко:
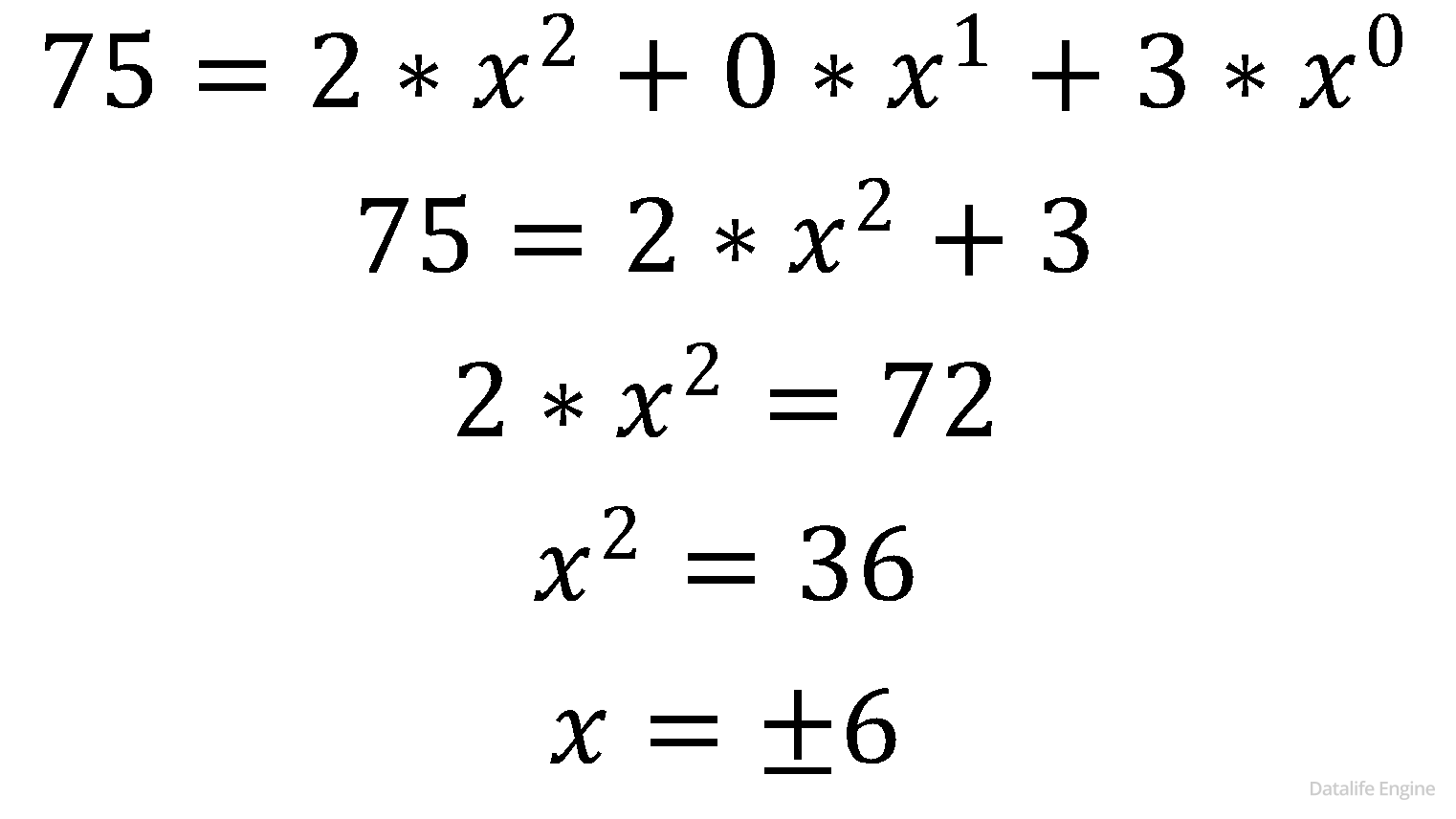
Оставляем положительный корень.
Ответ: 6.
Задача 1.6.2. Восьмеричное число 77 в некоторой системе счисления записывается как 70. Определите основание системы счисления.
Воспользуйтесь обратными переводами в 10-тичную систему счисления и составьте уравнение.
778 = 70x
7 * 8 + 7 = 7 * x
9 = x
Ответ. 9
Задача 1.6.3. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
Поступите аналогично предыдущей задаче. Старшие разряды не известны. Обозначьте их все разом буквой a и решите уравнение с параметром.
2910 = a5x
Далее сделаем обратный перевод:
29 = a * x + 5
a * x = 24
Уравнение имеет два неизвестных, поэтому решений несколько. Это уравнение напоминает задачи с параметром из ЕГЭ по математике, где а – это параметр. Посмотрим, какие у нас есть ограничения на х и а. Это целые числа,
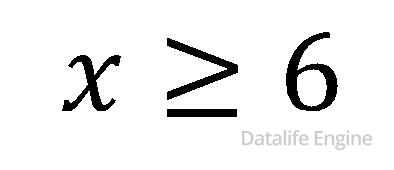
Последнее ограничение связано с тем, что в числе имеется цифра 5. А основание системы счисления не может быть меньше, чем цифра в числе.
Остается разложить число 24 на множители:
24 = 2 * 2 * 2 * 3
И из этих множителей записать все возможные произведения больше 5:
6, 8, 12, 24.
Заметьте, что само число 24 тоже входит в ответ.
Ответ. 6, 8, 12, 24.
Примечание. При решении этой задачи может возникнуть вопрос, насколько корректно обозначать буквой a несколько разрядов сразу?
Давайте проверим. Пусть будет три неизвестных разряда из цифр uvw
2910 = uvw5x
29 = u * x3 + v * x2 + w * x1 + 5 * x0
Вынесем за скобку x
29 = (u * x2 + v * x1 + w) * x + 5
Обозначим:
a = u * x2 + v * x1 + w
И мы получим то же самое уравнение:
29 = a * x + 5
Задача 1.6.4. В некоторой системе счисления записи десятичных чисел 56 и 45 заканчиваются на 1. Определите основание системы счисления
Аналогично предыдущим задачам составьте систему уравнений.
Ошибка.
Если вы систему уравнений запишете как:
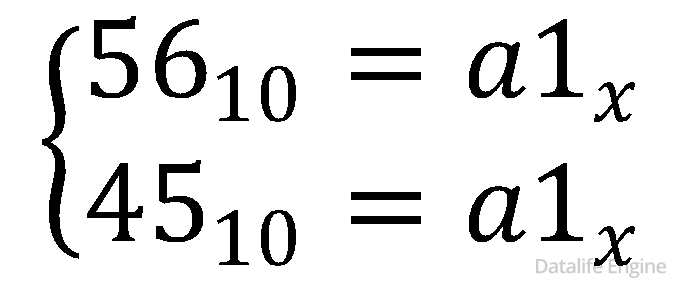
То вы будете не правы!
Неизвестные разряды не обязательно одинаковы.
Нужно их обозначить разными буквами:
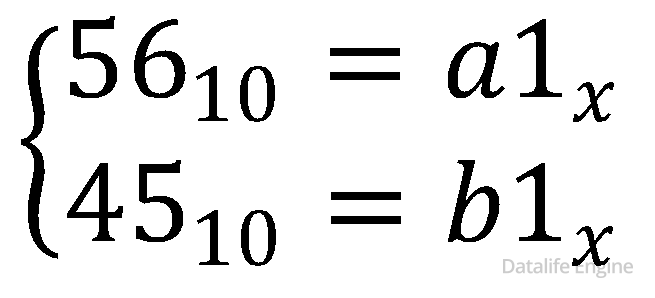
Далее применим обратный перевод:
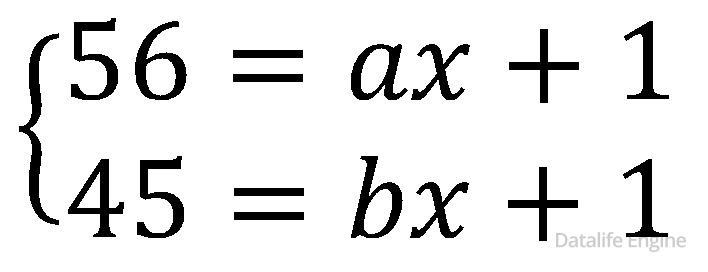
И получим
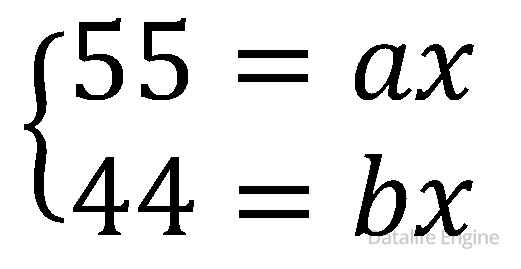
Разложим на множители:
5 * 11 = ax
4 * 11 = bx
Так как a, b, x – целые числа и x>1, то x=11.
Ответ. 11
Задача 1.6.5. В некоторых системах счисления записи десятичных чисел 113 и 89 заканчиваются на 1. Определите все возможные основания системы счисления.
Это усложнение предыдущей задачи.
Аналогично предыдущей задаче:
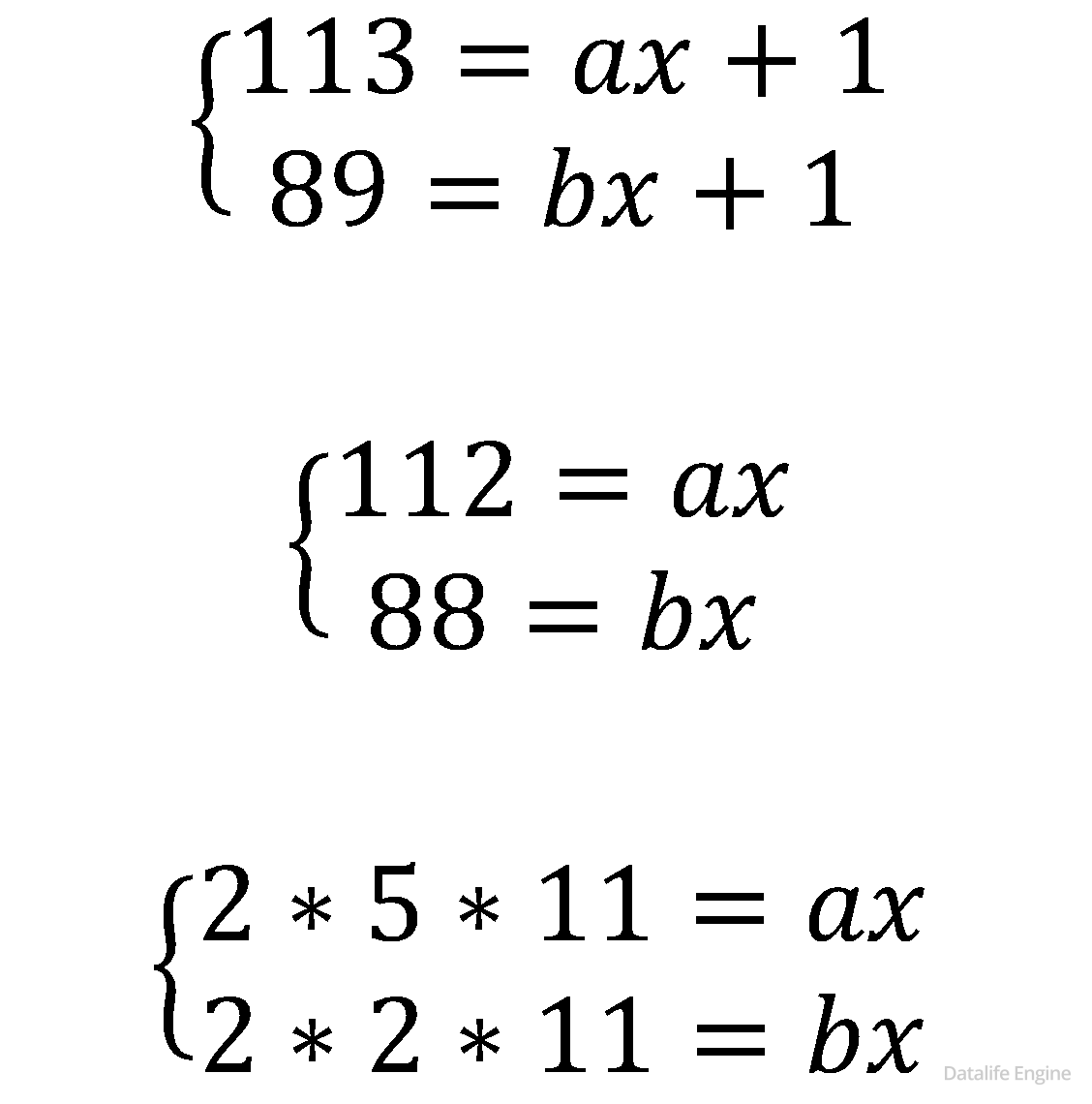
Теперь появляются варианты. Максимальное x будет состоять из общих множителей – это наибольший общий делитель: 2*11=22. Но x также может быть равен 2 и 11.
Ответ: 2,11,22
Задача 1.6.6. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 71 оканчивается на 13.
Аналогично предыдущим задачам:
7110 = а13х
Ошибка 1. Если вы дальше начнете решать так:
71 = ах + 13
То вы ошибетесь.
Продолжение хода решения.
Правильно так:
71 = ах2 + 1х + 3
Дальше знание математики может подвести. Захочется формально решать квадратное уравнение:
ах2 + х – 68 = 0
Тогда мы получим уравнение с параметром в дискриминанте и сложным подбором. Поступим, как и в предыдущие разы:
ах2 + х = 68
х(ах + 1) = 68
В левой части – произведение двух целых множителей. х > 3 (в числе есть цифра 3).
Ошибка 2. Далее можно сделать следующую ошибку – разложить 68 на множители и составить все подходящие произведения:
68 = 2 * 2 * 17
Кандидаты на ответ: 4, 17, 34, 68.
Но если мы проверим, например, 34, сделав прямой перевод каскадным делением:
То есть мы получим 32. В чем же дело? В том, что второй множитель имеет сложную структуру, в которую входит x.
Продолжение хода решения.
Сделаем более тщательный отбор:
|
x
|
ax+1
|
вывод
|
|
68
|
1=0*x+1
|
подходит
|
|
34
|
2=?
|
невозможно
|
|
17
|
4=?
|
невозможно
|
|
4
|
17=4*x+1
|
подходит
|
Ответ: 4, 68
Задача 1.6.7. Укажите наименьшее основание системы счисления, в которой запись числа 70 трехзначна.
Обозначьте неизвестные разряды тремя буквами. Попробуйте составить признак того, что число трехзначное и четырехзначное.
В отличие от предыдущих задач, поскольку мы знаем количество разрядов, обозначим каждый разряд своей буквой:
7010 = abcx
Сделаем обратный перевод:
70 = a * x2 + b * x1 + c * x0
Значение b и c нас не интересует. Они могут и равняться 0. Нам важен сам факт наличия разрядов. Поэтому мы можем превратить уравнение в неравенство:
70 = a * x2 + b * x + c ≥ a * x2
Значение a нам тоже искать не нужно. В минимальном случае a=1. Продолжим цепочку неравенств:
70 = a * x2 + b * x + c ≥ a * x2 ≥ x2
То есть:
x2 ≤ 70
Это признак того, что разрядов три или больше.
Наибольшее значение x = 8. Но нам нужно найти наименьшее. Очевидно, что долго уменьшать основание мы не можем. Число перестанет быть трехзначным и станет четырехзначным. В процессе выписывания таблицы с разными системами счисления у вас уже должно было появиться «чувство систем счисления». Какое же условие для того, чтобы число стало четырехзначным? По аналогии с приведенным условием на трехзначность:
x3 ≤ 70
Если вы это не поняли, проделайте аналогичные рассуждения, представив число 70 в виде четырех цифр, обозначенных буквами.
Условие четырехзначности должно быть ложным, следовательно:
x3 > 70
Соединим два неравенства вместе:
x2 ≤ 70 < x3
Рассмотрим таблицу квадратов и кубов:
|
Число
|
Квадрат
|
куб
|
|
9
|
81
|
3159
|
|
8
|
64
|
512
|
|
7
|
49
|
343
|
|
6
|
36
|
216
|
|
5
|
25
|
125
|
|
4
|
16
|
64
|
Видно, что минимальное подходящее основание – 5.
Ответ: 5.
Задача 1.6.8. Запись числа 338 в системе счисления с основанием x содержит три цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Это самая сложная задача на системы счисления. Она объединяет в себе все идеи из задач на неизвестные основания систем счисления.
Как и в предыдущих задачах, запишем:
33810 = ab2x
Делаем обратный перевод:
338 = ax2 + 1x + 3
336 = ax2 + x
Сделаем оценку, как в предыдущей задаче:
336 = ax2 + x > ax2 ≥ x2
x2 < 336
Корень нацело не извлекается, сделаем примерную оценку:
x < 18
Как в первой задаче, разложим 336 на множители:
336 = 2 * 2 * 2 * 2 * 3 * 7
Наиболее близкое к 18 число составлено из множителей:
х = 2 * 2 * 2 * 2 = 16
Ответ: 16.
Задача 1.6.9. Укажите основание системы счисления, в которой запись числа 94
начинается на 23.
Предположим, это число – ровно 23, тогда:
9410 = 23х
94 = 2x + 3
2x = 91
91 на 2 без остатка не делится. Поэтому этот случай невозможен.
Предположим, что число – трехзначное, тогда:
9410 = 23ах
94 = 2х2 + 3х + а
Оценим диапазон x, чтобы число было трехзначным:
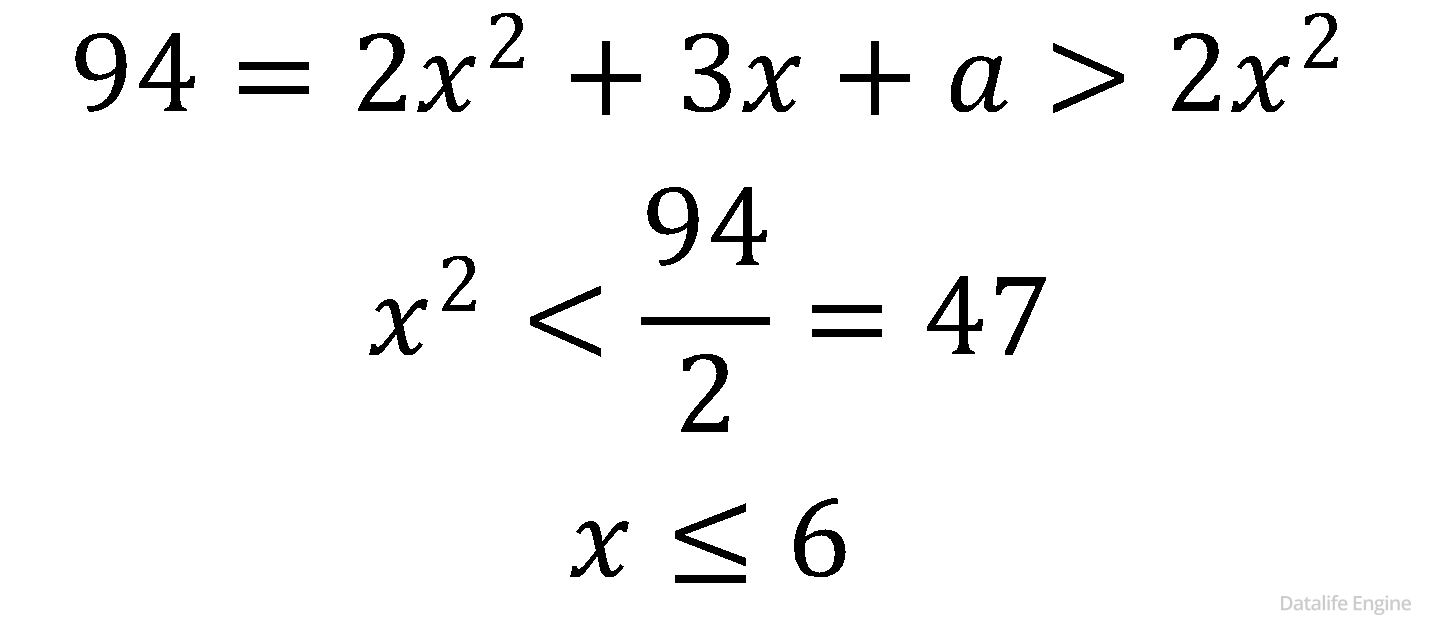
С учетом имеющейся максимальной цифры в числе – 3, имеем ограничение на систему счисления снизу:
4 ≤ x ≤ 6
Проверим для 4:
2 * 16 + 3 * 4 + a = 94
a = 60.
Это невозможно, так как a – цифра в четверичной системе.
Проверим 5:
2 * 25 + 3 * 5 + a = 94
a = 29.
Проверим 6:
2 * 36 + 3 * 6 + a = 94
a = 4 < 6.
Поэтому 6 – подходит.
Предположим, в числе четыре цифры:
9410 = 23abx
94 = 2x3 + 3x2 + ax + b
Оценим диапазон x, чтобы число было четырехзначным:
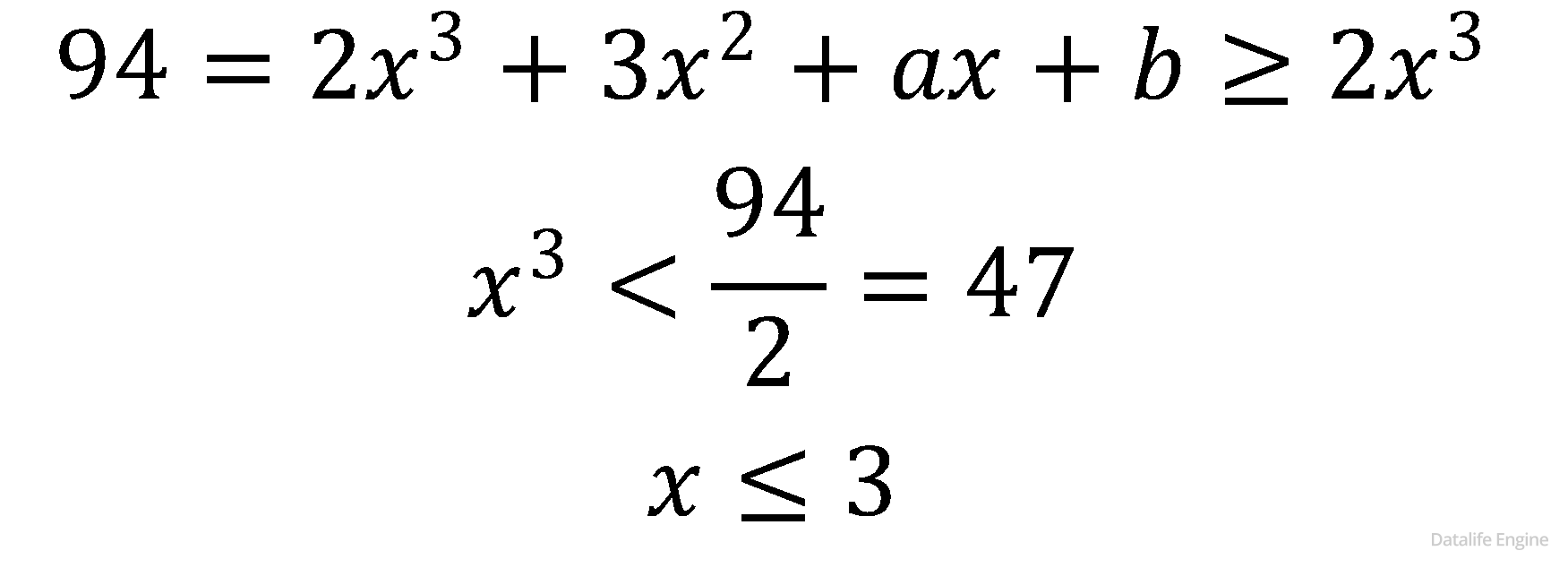
Это невозможно, так как в числе есть цифра три.
Ответ: 6.
Задача 1.6.10. Запись числа N в системе счисления с основанием 6 содержит две цифры, запись этого числа в системе счисления с основанием 5 содержит три цифры, а запись в системе счисления с основанием 11 заканчивается на 1. Чему равно N?
Для первых двух условий воспользуйтесь оценками, как в задаче 1.5.6. Для последнего условия - как в задаче 1.5.2.
Рассмотрим условие «Запись числа N в системе счисления с основанием 6 содержит две цифры»:
N10 = ab6 = a * 6 + b ≥ 6
Это нижнее ограничение, рассмотрим верхнее ограничение. Если бы число в системе с основанием 6 было бы трехзначным, то:
N10 = abc6 = a * 62 + b * 6 + c ≥ 36
Что не должно быть верным по условию, значит:
6 ≤ N ≤ 36
Рассмотрим условие «запись этого числа в системе счисления с основанием 5 содержит три цифры». Аналогично предыдущему условию:
52 ≤ N ≤ 53
25 ≤ N ≤ 125
Объединяем оценки двух условий:
25 ≤ N ≤ 36
Рассмотрим последнее условие «запись в системе счисления с основанием 11 заканчивается на 1»:
N10 = a111 = a * 11 + 1
Подставим это выражение в полученную оценку по первому и второму условию:
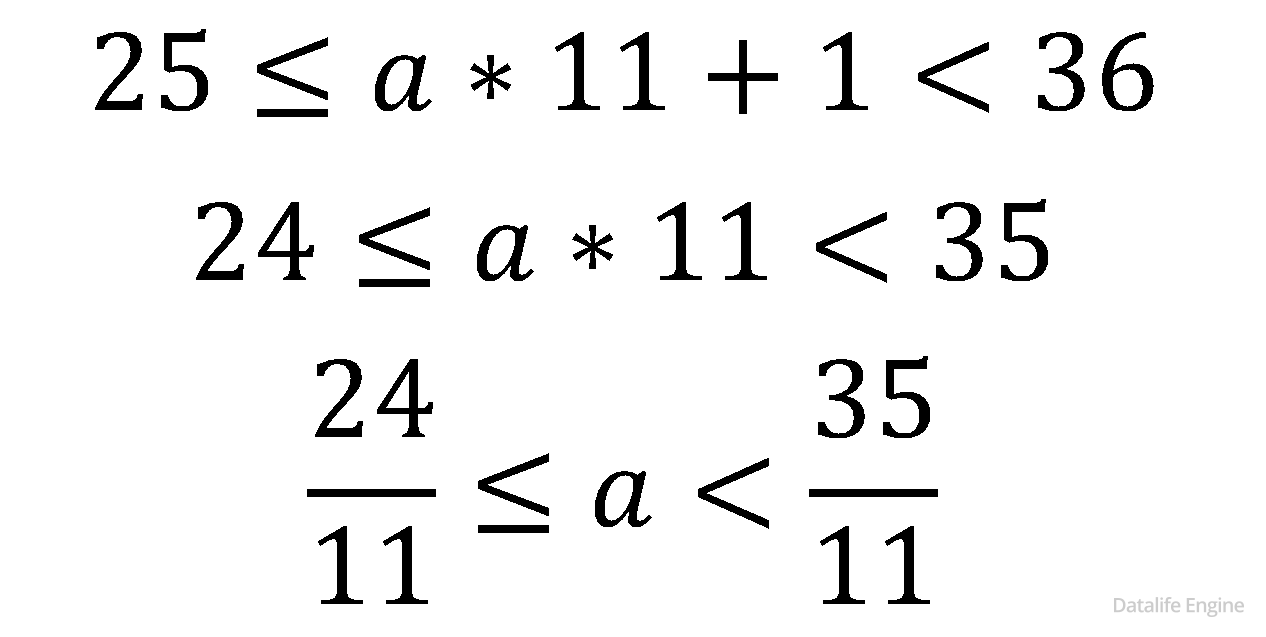
С учетом того, что мы имеем дело с целыми числами:
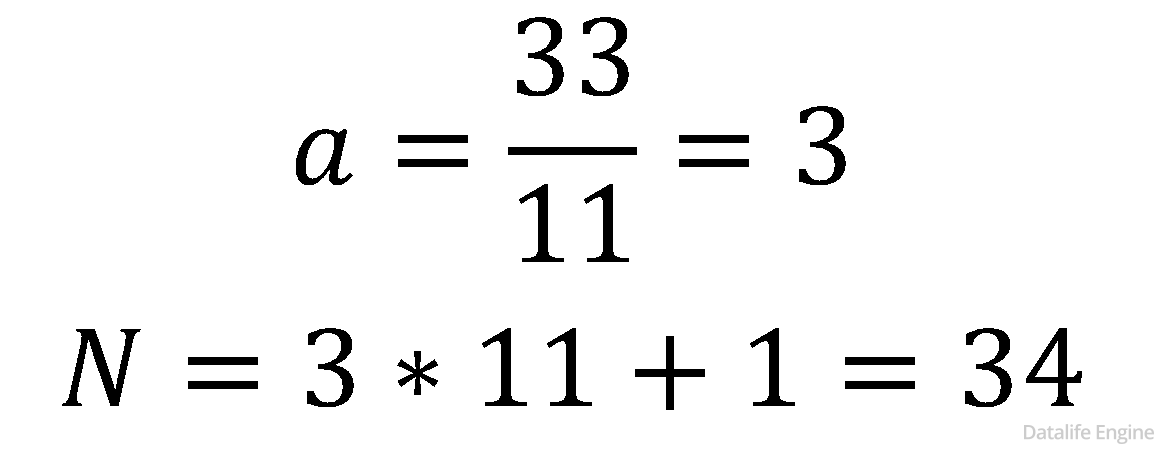
Ответ: 34.
Мы прорешали все задачи из ЕГЭ на системы счисления в чистом виде, за исключением небольших вариаций. Но также системы счисления применяются в ряде других задач во многих разделах ЕГЭ: логике (задачи на отрезки), IP-адресации, анализе программ и очень часто в кодировании.