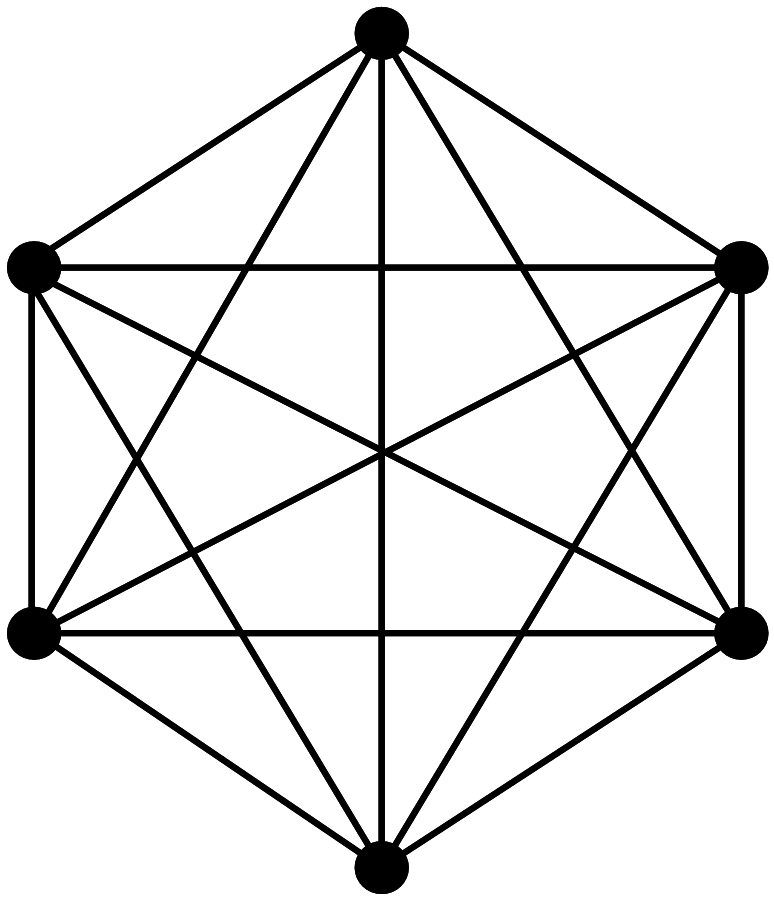
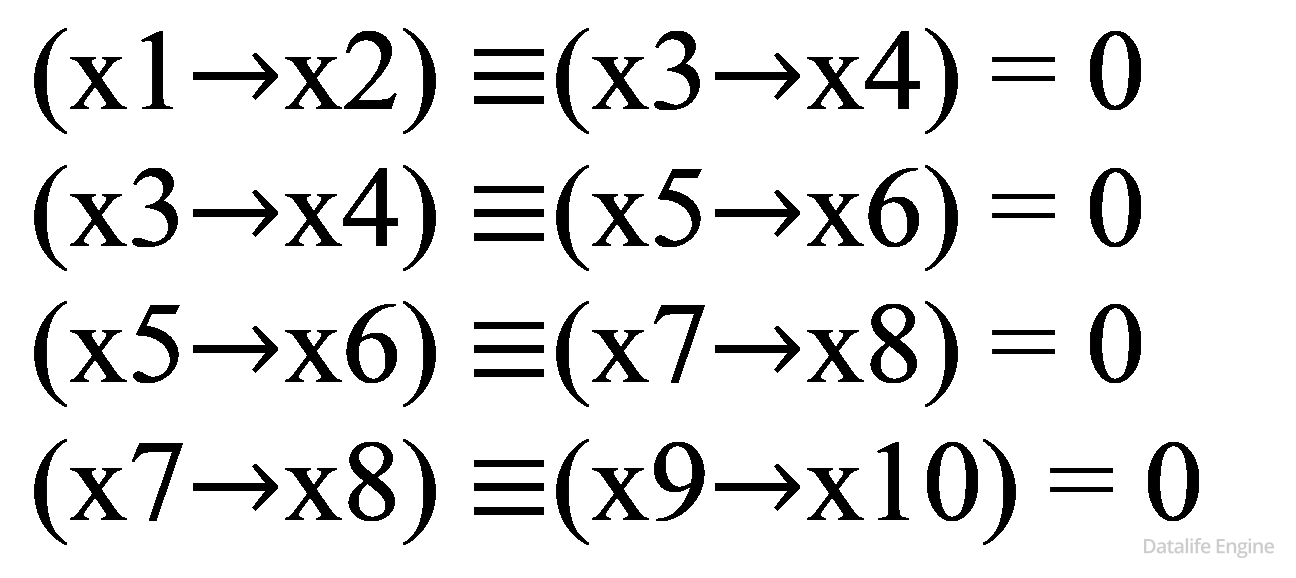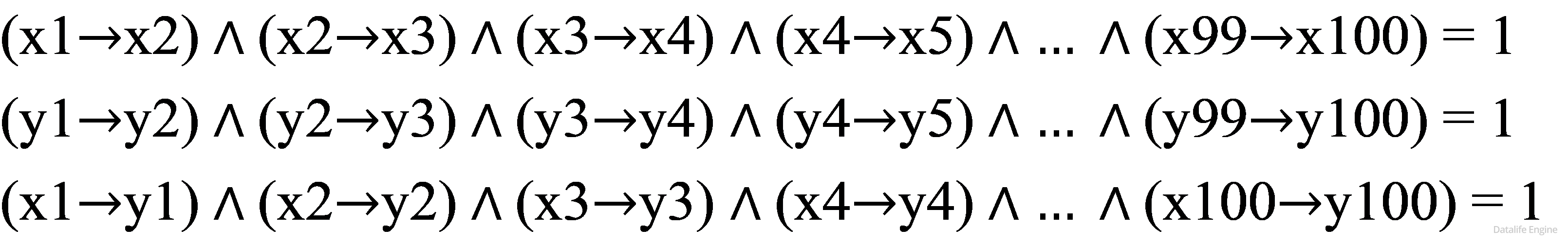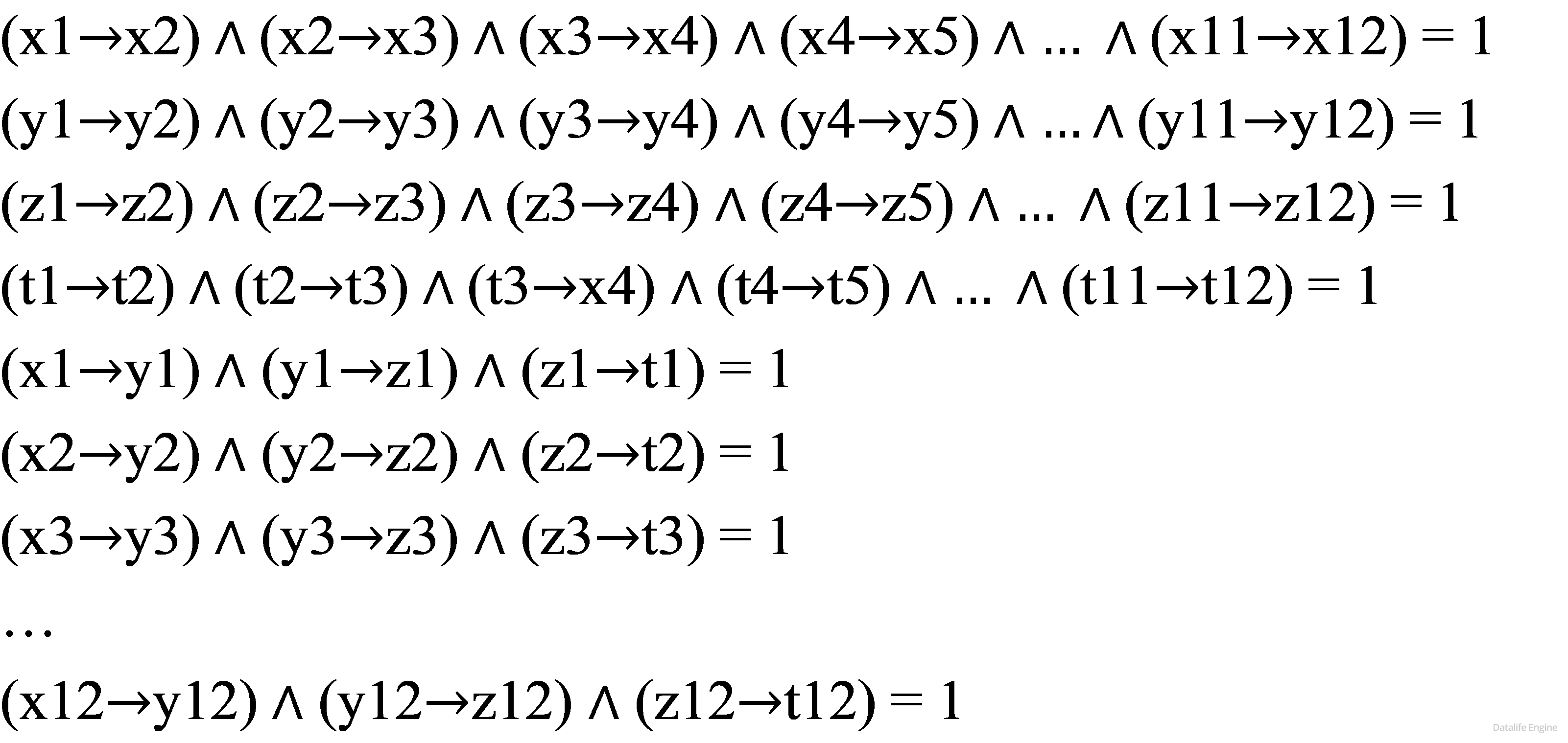7. КОМБИНАТОРИКА
Начала комбинаторики мной были изложены во втором разделе – «Кодирование» (параграф «Основы комбинаторики»). Вместе с тем она широко применяется в последующих задачах. Так, мы встречали комбинаторику в задачах на количество программ и чисел, на логические уравнения, на IP-адресацию.
Вначале мы сделаем обзор таких задач. Для удобства сравнения формулировки задач сведены в таблицы. В идеале тренированный решать ЕГЭ читатель должен сразу по формулировкам задач видеть разницу в ходе их решения. Но, как показывает мой опыт, ученики успевают забыть комбинаторику при переходе к задачам на программирование (она, кстати, встречается и там). Поэтому повторение не бывает лишним даже для способных учеников. Целесообразно прорешать эти задачи за одно занятие для образования системных связей (может потребоваться 120 минут).
Далее идут задачи, которые я усложнил, чтобы подчеркнуть их «комбинаторную суть» и сделать невозможным угадывание ответа. Кроме того, приводится несколько олимпиадных задач (не из ЕГЭ). Их полезно прорешать тем ученикам, кто нацелился получить максимальный балл. Они формируют определенный стиль мышления и находчивость, которая позволит не растеряться, если вдруг на ЕГЭ встретится незнакомая задача.
В общем, в этом разделе, как и в следующем, мы делаем второй круг по сложным и интересным задачам ЕГЭ, интегрирующий знания из разных разделов информатики (прикладной математики).